Podwójny wykres
W matematycznej dyscyplinie teorii grafów graf dualny płaskiego wykresu G to graf, który ma wierzchołek dla każdej ściany G. Wykres podwójny ma krawędź dla każdej pary ścian w G , które są oddzielone od siebie krawędzią, oraz samopętlę, gdy ta sama ściana pojawia się po obu stronach krawędzi. Zatem każda krawędź e G ma odpowiadającą jej podwójną krawędź, której punktami końcowymi są podwójne wierzchołki odpowiadające ścianom po obu stronach e . Definicja dualności zależy od wyboru osadzania grafu G , więc jest to właściwość grafów płaskich (grafów, które są już osadzone w płaszczyźnie), a nie grafów planarnych (grafów, które mogą być osadzone, ale dla których osadzanie jest jeszcze nieznany). Ogólnie w przypadku grafów planarnych może istnieć wiele grafów podwójnych, w zależności od wyboru płaskiego osadzania wykresu.
Historycznie, pierwszą rozpoznaną formą dwoistości grafów było powiązanie brył platońskich w pary podwójnych wielościanów . Dualność grafów jest topologicznym uogólnieniem geometrycznych koncepcji podwójnych wielościanów i podwójnych teselacji , a z kolei jest uogólniona kombinatorycznie przez koncepcję podwójnej matroidy . Odmiany dwoistości grafów planarnych obejmują wersję dwoistości dla grafów skierowanych i dwoistość dla grafów osadzonych na niepłaskich dwuwymiarowych powierzchniach.
Tych pojęć grafów dualnych nie należy mylić z innym pojęciem, wykresem podwójnym lub liniowym od krawędzi do wierzchołka.
Termin dualny jest używany, ponieważ właściwość bycia grafem dualnym jest symetryczna , co oznacza, że jeśli H jest grafem podwójnym połączonego grafu G , to G jest grafem podwójnym H. Omawiając podwójność wykresu G , sam wykres G można nazwać „grafem pierwotnym”. Wiele innych właściwości i struktur grafów można przetłumaczyć na inne naturalne właściwości i struktury liczby podwójnej. Na przykład cykle są dualne względem cięć , drzewa rozpinające są dualne względem dopełnień drzew rozpinających, a proste grafy (bez równoległych krawędzi lub pętli własnych ) są dualne względem grafów połączonych trzema krawędziami .
Dualność grafów może pomóc w wyjaśnieniu struktury labiryntów i zlewni . Wykresy dualne znalazły również zastosowanie w wizji komputerowej , geometrii obliczeniowej , generowaniu siatki i projektowaniu układów scalonych .
Przykłady
Cykle i dipole
Unikalne płaskie osadzenie wykresu cyklu dzieli płaszczyznę tylko na dwa obszary, wewnątrz i na zewnątrz cyklu, zgodnie z twierdzeniem Jordana o krzywej . Jednak w n -cyklu te dwa regiony są oddzielone od siebie n różnymi krawędziami. Dlatego graf dualny n -cyklu jest multigrafem z dwoma wierzchołkami (podwójnymi względem regionów), połączonymi ze sobą n krawędziami podwójnymi. Taki graf nazywany jest grafem wielokrotnym, sprzężeniem lub czasem dipolem . I odwrotnie, wykres dipola podwójnego do n -krawędziowego jest n -cyklem.
Podwójne wielościany
Zgodnie z twierdzeniem Steinitza każdy graf wielościenny (wykres utworzony przez wierzchołki i krawędzie trójwymiarowego wielościanu wypukłego ) musi być płaski i połączony 3 wierzchołkami , a każdy graf płaski połączony 3 wierzchołkami pochodzi z wielościanu wypukłego w tą drogą. Każdy trójwymiarowy wypukły wielościan ma podwójny wielościan ; podwójny wielościan ma wierzchołek dla każdej ściany oryginalnego wielościanu, z dwoma podwójnymi wierzchołkami sąsiadującymi, ilekroć odpowiednie dwie ściany mają wspólną krawędź. Ilekroć dwa wielościany są podwójne, ich grafy również są podwójne. Na przykład bryły platońskie występują w podwójnych parach, z ośmiościanem podwójnym do sześcianu, dwunastościanem podwójnym do dwudziestościanu i czworościanem podwójnym do siebie. Dualizm wielościanów można również rozszerzyć na dualność polytopów o wyższych wymiarach , ale to rozszerzenie dualności geometrycznej nie ma wyraźnych powiązań z dualnością teorii grafów.
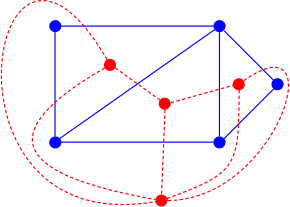
Grafy samodualne
Mówimy, że graf płaski jest samodwoisty, jeśli jest izomorficzny ze swoim grafem dualnym. Wykresy kołowe zapewniają nieskończoną rodzinę grafów samodualnych pochodzących z samodualnych wielościanów ( piramidów ). Jednak istnieją również grafy samodualne, które nie są wielościenne, takie jak ten pokazany. Servatius i Christopher (1992) opisują dwie operacje, adhezję i eksplozję, które można wykorzystać do skonstruowania samodualnego grafu zawierającego dany graf planarny; na przykład pokazany wykres samodualny można skonstruować jako adhezję czworościanu z jego dualem.
wzoru Eulera wynika , że każdy graf samodualny z n wierzchołkami ma dokładnie 2 n − 2 krawędzie. Każdy prosty samodualny graf planarny zawiera co najmniej cztery wierzchołki trzeciego stopnia, a każde samodualne osadzenie ma co najmniej cztery trójkątne ściany.
Nieruchomości
Wiele naturalnych i ważnych pojęć w teorii grafów odpowiada innym równie naturalnym, ale różnym koncepcjom w grafie dualnym. Ponieważ liczba podwójna połączonego wykresu płaskiego jest izomorficzna z grafem pierwotnym, każda z tych par jest dwukierunkowa: jeśli koncepcja X na grafie planarnym odpowiada koncepcji Y na grafie podwójnym, to koncepcja Y na grafie planarnym odpowiada koncepcja X w dualności.
Wykresy proste a multigrafy
Podwójny prosty graf nie musi być prosty: może mieć pętle własne (krawędź z obydwoma punktami końcowymi w tym samym wierzchołku) lub wiele krawędzi łączących te same dwa wierzchołki, co było już widoczne na przykładzie multigrafów dipolowych, które są dualne do wykresy cykli. Jako szczególny przypadek omówionej poniżej dualności cyklu cięcia, mostki grafu planarnego G są w relacji jeden do jednego z samopętlami grafu dualnego. Z tego samego powodu para równoległych krawędzi w podwójnym multigrafie (to znaczy cyklu o długości 2) odpowiada 2-krawędziowemu zestawowi cięć w grafie pierwotnym (parze krawędzi, których usunięcie powoduje rozłączenie wykresu). Dlatego graf planarny jest prosty wtedy i tylko wtedy, gdy jego podwójny nie ma zestawów cięć 1- lub 2-krawędziowych; to znaczy, jeśli jest połączony 3-krawędziowo . Proste grafy planarne, których liczby podwójne są proste, to dokładnie 3-krawędziowe proste grafy planarne. Ta klasa grafów obejmuje klasę prostych grafów planarnych połączonych trzema wierzchołkami , ale nie jest tożsama. Na przykład figura przedstawiająca graf samodualny jest połączona trzema krawędziami (a zatem jej podwójność jest prosta), ale nie jest połączona przez trzy wierzchołki.
Wyjątkowość

Ponieważ graf dualny zależy od określonego osadzania, graf dualny grafu planarnego nie jest unikalny w tym sensie, że ten sam graf planarny może mieć nieizomorficzne grafy dualne. Na rysunku niebieskie wykresy są izomorficzne, ale ich podwójne czerwone wykresy nie. Górna czerwona podwójna ma wierzchołek o stopniu 6 (odpowiadającym zewnętrznej powierzchni niebieskiego wykresu), podczas gdy na dolnym czerwonym wykresie wszystkie stopnie są mniejsze niż 6.
Hassler Whitney wykazał, że jeśli graf jest 3-spójny, to osadzanie, a tym samym graf dualny, jest wyjątkowy. Zgodnie z twierdzeniem Steinitza grafy te są dokładnie grafami wielościennymi , grafami wypukłych wielościanów. Graf planarny jest spójny w 3 wierzchołkach wtedy i tylko wtedy, gdy jego graf dualny jest spójny w 3 wierzchołkach. Mówiąc bardziej ogólnie, graf planarny ma unikalne osadzenie, a zatem także unikalny podwójny, wtedy i tylko wtedy, gdy jest to podpodział grafu planarnego połączonego z 3 wierzchołkami (wykres utworzony z grafu planarnego połączonego z 3 wierzchołkami przez zastąpienie niektóre jego krawędzie ścieżkami). W przypadku niektórych grafów planarnych, które nie są połączone w 3 wierzchołki, takich jak kompletny graf dwudzielny K 2,4 , osadzanie nie jest unikalne, ale wszystkie osadzenia są izomorficzne. Kiedy tak się dzieje, wszystkie grafy dualne są odpowiednio izomorficzne.
Ponieważ różne osadzenia mogą prowadzić do różnych grafów dualnych, testowanie, czy jeden graf jest grafem podwójnym innego (bez wcześniejszej znajomości ich osadzeń), jest nietrywialnym problemem algorytmicznym . W przypadku grafów dwupołączonych można to rozwiązać w czasie wielomianowym, używając drzew SPQR grafów do skonstruowania postaci kanonicznej dla relacji równoważności posiadania wspólnej wzajemnej liczby podwójnej. Na przykład dwa czerwone wykresy na ilustracji są równoważne zgodnie z tą zależnością. Jednak w przypadku grafów planarnych, które nie są bispójne, relacja ta nie jest relacją równoważności, a problem testowania wzajemnej dualności jest NP-zupełny .
Cięcia i cykle
Zestaw przekrojów w dowolnie połączonym grafie to podzbiór krawędzi zdefiniowany na podstawie podziału wierzchołków na dwa podzbiory, poprzez włączenie krawędzi do podzbioru, gdy ma on jeden punkt końcowy po każdej stronie podziału. Usunięcie krawędzi zestawu przekrojów nieuchronnie dzieli wykres na co najmniej dwa połączone komponenty. Minimalny zbiór przekrojów (zwany także wiązaniem) to zbiór przekrojów, którego właściwość polega na tym, że każdy właściwy podzbiór zbioru przekrojów sam w sobie nie jest przekrojem. Minimalny zestaw cięć połączonego grafu z konieczności rozdziela jego wykres na dokładnie dwa składniki i składa się z zestawu krawędzi, które mają jeden punkt końcowy w każdym składniku. Prosty cykl to spójny podgraf , w którym każdy wierzchołek cyklu przypada dokładnie na dwie krawędzie cyklu.
W spójnym grafie planarnym G każdy prosty cykl G odpowiada minimalnemu zestawowi cięć w dualności G i odwrotnie. Można to postrzegać jako formę twierdzenia o krzywej Jordana : każdy prosty cykl dzieli ściany G na ściany wewnętrzne cyklu i ściany zewnętrzne cyklu, a liczby podwójne krawędzi cyklu są dokładnie krawędzie przechodzące z wnętrza na zewnątrz. Obwód dowolnego wykresu planarnego (rozmiar jego najmniejszego cyklu) jest równy łączności krawędziowej jego wykresu dualnego (rozmiar jego najmniejszego przekroju).
Ta dwoistość rozciąga się od pojedynczych zestawów przekrojów i cykli do zdefiniowanych na ich podstawie przestrzeni wektorowych . Przestrzeń cykli grafu jest zdefiniowana jako rodzina wszystkich podgrafów, które mają parzysty stopień w każdym wierzchołku; można go postrzegać jako przestrzeń wektorową nad dwuelementowym polem skończonym , przy czym symetryczna różnica dwóch zestawów krawędzi działa jako operacja dodawania wektorów w przestrzeni wektorowej. Podobnie przestrzeń cięcia grafu jest zdefiniowana jako rodzina wszystkich zbiorów, z dodaniem wektorów zdefiniowanym w ten sam sposób. Wtedy przestrzeń cyklu dowolnego grafu planarnego i przestrzeń cięcia jego grafu dualnego są izomorficzne jako przestrzenie wektorowe. Zatem ranga grafu planarnego ( wymiar jego przestrzeni cięcia) jest równa liczbie cyklotomicznej jego dualności (wymiar jego przestrzeni cykli) i odwrotnie. Podstawa cykliczna grafu to zbiór prostych cykli tworzących bazę przestrzeni cykli (każdy podgraf parzystego stopnia można utworzyć dokładnie w jeden sposób jako różnicę symetryczną niektórych z tych cykli). W przypadku ważonych krawędziami (z wystarczająco ogólnymi wagami, aby żadne dwa cykle nie miały tej samej wagi) podstawa wykresu minimalnej wagi cyklu jest podwójna z drzewem Gomory -Hu wykresu podwójnego, zbiorem zagnieżdżonych cięć, które razem obejmują minimalne cięcie oddzielające każdą parę wierzchołków w grafie. Każdy cykl w podstawie cyklu minimalnej wagi ma zestaw krawędzi, które są podwójne do krawędzi jednego z cięć w drzewie Gomory-Hu. Gdy wagi cykli mogą być powiązane, podstawa cyklu minimalnej wagi może nie być unikalna, ale w tym przypadku nadal prawdą jest, że drzewo Gomory-Hu na wykresie podwójnym odpowiada jednej z podstaw cyklu minimalnej wagi na wykresie.
W skierowanych grafach planarnych proste cykle skierowane są podwójne do ukierunkowanych cięć (podział wierzchołków na dwa podzbiory w taki sposób, że wszystkie krawędzie biegną w jednym kierunku, z jednego podzbioru do drugiego). Silnie zorientowane grafy planarne (wykresy, których podstawowy graf nieskierowany jest spójny i w których każda krawędź należy do cyklu) są dualne do skierowanych grafów acyklicznych , w których żadna krawędź nie należy do cyklu. Innymi słowy, silne orientacje połączonego grafu planarnego (przypisania kierunków do krawędzi grafu, które dają silnie spójny graf ) są dualne do orientacji acyklicznych (przypisania kierunków, które tworzą skierowany wykres acykliczny ). W ten sam sposób dijoins (zestawy krawędzi, które zawierają krawędź z każdego ukierunkowanego cięcia) są podwójne do zestawów łuków sprzężenia zwrotnego (zestawy krawędzi, które zawierają krawędź z każdego cyklu).
Rozpinające się drzewa
Drzewo rozpinające można zdefiniować jako zbiór krawędzi, który wraz ze wszystkimi wierzchołkami grafu tworzy spójny i acykliczny podgraf. Ale przez dualność cyklu cięcia, jeśli zbiór S krawędzi w grafie planarnym G jest acykliczny (nie ma cykli), to zbiór krawędzi podwójnych do S nie ma cięć, z czego wynika, że komplementarny zbiór krawędzi podwójnych (podwójne krawędzie, które nie są w S ) tworzy spójny podgraf. Symetrycznie, jeśli S jest spójny, to krawędzie podwójne do dopełnienia S tworzą podgraf acykliczny. Dlatego, gdy S ma obie właściwości – jest spójny i acykliczny – to samo dotyczy zbioru komplementarnego w grafie dualnym. Oznacza to, że każde drzewo rozpinające G jest komplementarne do drzewa rozpinającego grafu dualnego i odwrotnie. Zatem krawędzie dowolnego grafu planarnego i jego dualnego można razem podzielić (na wiele różnych sposobów) na dwa drzewa rozpinające, jedno w pierwotnym i jedno w podwójnym, które razem rozciągają się na wszystkie wierzchołki i ściany grafu, ale nigdy krzyżować się. W szczególności minimalne drzewo rozpinające G jest komplementarne do maksymalnego drzewa rozpinającego wykresu podwójnego . Jednak to nie działa w przypadku drzew o najkrótszej ścieżce , nawet w przybliżeniu: istnieją grafy planarne takie, że dla każdej pary drzewa rozpinającego na grafie i komplementarnego drzewa rozpinającego na grafie podwójnym przynajmniej jedno z dwóch drzew ma odległości które są znacznie dłuższe niż odległości na jego wykresie.
Przykład tego typu rozkładu na przeplatające się drzewa można zobaczyć w niektórych prostych typach labiryntów , z jednym wejściem i bez rozłączonych elementów ścian. W tym przypadku zarówno ściany labiryntu, jak i przestrzeń między nimi przybierają formę matematycznego drzewa. Jeśli wolna przestrzeń labiryntu jest podzielona na proste komórki (takie jak kwadraty siatki), wówczas ten system komórek można postrzegać jako osadzanie grafu planarnego, w którym drzewiasta struktura ścian tworzy rozpinające drzewo wykres i struktura drzewiasta wolnej przestrzeni tworzy drzewo rozpinające grafu dualnego. Podobne pary przeplatających się drzew można również zobaczyć w drzewiastym wzorze strumieni i rzek w zlewni oraz w podwójnym drzewiastym wzorze grzbietów oddzielających strumienie.
Ten podział krawędzi i ich liczb podwójnych na dwa drzewa prowadzi do prostego dowodu wzoru Eulera V - E + F = 2 dla grafów planarnych z wierzchołkami V , krawędziami E i ścianami F. Każde drzewo rozpinające i jego komplementarne podwójne drzewo rozpinające dzielą krawędzie na dwa podzbiory odpowiednio krawędzi V - 1 i F - 1 , a dodanie rozmiarów dwóch podzbiorów daje równanie
- mi = ( V - 1) + ( fa - 1)
które można przeorganizować, tworząc wzór Eulera. Według Duncana Sommerville'a ten dowód wzoru Eulera wynika z Geometrie der Lage KGC Von Staudt (Nürnberg, 1847).
W nieplanarnych osadzaniach powierzchniowych zestaw podwójnych krawędzi komplementarnych do drzewa rozpinającego nie jest drzewem rozpinającym. Zamiast tego ten zestaw krawędzi jest połączeniem podwójnego drzewa rozpinającego z małym zestawem dodatkowych krawędzi, których liczba jest określona przez rodzaj powierzchni, na której osadzony jest wykres. Dodatkowe krawędzie w połączeniu ze ścieżkami w drzewach rozpinających można wykorzystać do wygenerowania podstawowej grupy powierzchni.
Dodatkowe właściwości
Dowolna formuła zliczania obejmująca wierzchołki i ściany, która jest ważna dla wszystkich grafów planarnych, może zostać przekształcona przez planarną dualność w równoważną formułę, w której role wierzchołków i ścian zostały zamienione. Jednym z przykładów jest wzór Eulera, który jest samodwoisty. Inny podany przez Harary'ego lemat o uzgadnianiu , zgodnie z którym suma stopni wierzchołków dowolnego grafu jest równa dwukrotności liczby krawędzi. W swojej podwójnej formie lemat ten stwierdza, że w grafie płaskim suma liczb boków ścian grafu jest równa dwukrotności liczby krawędzi.
Wykres środkowy wykresu płaskiego jest izomorficzny z wykresem środkowym jego podwójnego. Dwa grafy planarne mogą mieć izomorficzne grafy środkowe tylko wtedy, gdy są względem siebie dualne.
Graf planarny z czterema lub więcej wierzchołkami jest maksymalny (nie można dodać więcej krawędzi przy zachowaniu planarności) wtedy i tylko wtedy, gdy jego graf podwójny jest zarówno spójny z 3 wierzchołkami, jak i 3-regularny .
Spójny graf planarny jest eulerowski (ma parzysty stopień w każdym wierzchołku) wtedy i tylko wtedy, gdy jego podwójny graf jest dwudzielny . Cykl Hamiltona w grafie planarnym G odpowiada podziałowi wierzchołków grafu dualnego na dwa podzbiory (wewnętrzny i zewnętrzny cyklu), których indukowanymi podgrafami są oba drzewa. W szczególności przypuszczenie Barnette'a dotyczące hamiltoniczności sześciennych dwudzielnych grafów wielościennych jest równoważne przypuszczeniu, że każdy maksymalny planarny graf Eulera można podzielić na dwa drzewa indukowane.
Jeśli graf planarny G ma wielomian Tutte'a TG ( x , y ) , to wielomian Tutte'a jego wykresu dualnego otrzymuje się przez zamianę x i y . Z tego powodu, jeśli jakaś konkretna wartość wielomianu Tutte dostarcza informacji o pewnych typach struktur w G , to zamiana argumentów na wielomian Tutte da odpowiednie informacje dla struktur dualnych. Na przykład liczba silnych orientacji to TG TG (0,2) , ( 2,0) a liczba orientacji acyklicznych to . W przypadku grafów planarnych bez mostków kolorowanie grafów za pomocą k kolorów odpowiada przepływom nigdzie zerowym modulo k na wykresie dualnym. Na przykład twierdzenie o czterech kolorach (istnienie 4-kolorowania dla każdego wykresu planarnego) można wyrazić równoważnie jako stwierdzenie, że liczba podwójna każdego bezmostkowego grafu planarnego ma nigdzie zerowy przepływ 4. Liczbę k -kolorów oblicza się (z dokładnością do łatwego do obliczenia współczynnika) przez wartość wielomianu Tutte'a T G (1 − k ,0) i podwójnie liczbę k -przepływów nigdzie niezerowych oblicza się przez T G (0,1 − k ) .
Wykres st -planarny to spójny graf planarny wraz z dwubiegunową orientacją tego wykresu, orientacją, która czyni go acyklicznym z jednym źródłem i pojedynczym ujściem, z których oba muszą znajdować się na tej samej ścianie. Taki graf można przekształcić w silnie spójny graf, dodając jeszcze jedną krawędź, od zlewu z powrotem do źródła, przez zewnętrzną ścianę. Liczba podwójna tego rozszerzonego grafu planarnego sama w sobie jest rozszerzeniem innego st -planarnego wykresu.
Wariacje
Grafy skierowane
Na skierowanym wykresie płaskim wykres podwójny można również skierować, ustawiając każdą krawędź podwójną o 90 ° zgodnie z ruchem wskazówek zegara od odpowiedniej krawędzi pierwotnej. Ściśle mówiąc, ta konstrukcja nie jest dualnością skierowanych grafów planarnych, ponieważ rozpoczynanie od grafu G i dwukrotne wzięcie podwójnego nie powoduje powrotu do samego G , ale zamiast tego konstruuje graf izomorficzny z transponowanym wykresem G , wykres utworzony z G poprzez odwrócenie wszystkich jego krawędzi. Czterokrotne uwzględnienie liczby podwójnej powoduje powrót do pierwotnego wykresu.
Słaby podwójny
Słaba liczba podwójna grafu płaskiego jest podgrafem grafu dualnego, którego wierzchołki odpowiadają ograniczonym ścianom grafu pierwotnego. Graf płaski jest planarny wtedy i tylko wtedy, gdy jego słabym dualem jest las . Dla dowolnego wykresu płaskiego G niech G + będzie multigrafem płaskim utworzonym przez dodanie pojedynczego nowego wierzchołka v na nieograniczonej ścianie G i połączenie v z każdym wierzchołkiem zewnętrznej ściany (wiele razy, jeśli wierzchołek pojawia się wiele razy na granica powierzchni zewnętrznej); wtedy G jest słabym dualem (płaskiego) dualu G + .
Nieskończone grafy i teselacje
Pojęcie dualności odnosi się zarówno do grafów nieskończonych osadzonych w płaszczyźnie, jak i do grafów skończonych. Należy jednak zachować ostrożność, aby uniknąć komplikacji topologicznych, takich jak punkty płaszczyzny, które nie są ani częścią otwartego obszaru odłączonego od grafu, ani częścią krawędzi lub wierzchołka grafu. Gdy wszystkie ściany są ograniczonymi obszarami otoczonymi cyklem grafu, nieskończone osadzanie grafu planarnego można również postrzegać jako teselację płaszczyzny , pokrycie płaszczyzny zamkniętymi dyskami (płytki teselacji), których wnętrza (ściany osadzania) są rozłącznymi otwartymi dyskami. Płaska dualność daje początek pojęciu podwójnej teselacji , teselacji utworzonej przez umieszczenie wierzchołka w środku każdej płytki i połączenie środków sąsiednich płytek.
Koncepcję podwójnej teselacji można również zastosować do podziału płaszczyzny na skończenie wiele obszarów. W tym przypadku jest to blisko spokrewnione, ale nie do końca tożsame z dwoistością grafów planarnych. Na przykład diagram Woronoja skończonego zbioru miejsc punktowych to podział płaszczyzny na wielokąty , w których jedno miejsce jest bliżej niż inne. Miejsca na wypukłym kadłubie wejścia dają początek nieograniczonym wielokątom Woronoja, z których dwa boki są raczej nieskończonymi promieniami niż skończonymi odcinkami linii. Podwójnością tego diagramu jest triangulacja danych wejściowych Delaunaya , graf planarny, który łączy dwa miejsca krawędzią, ilekroć istnieje okrąg zawierający te dwa miejsca i żadnych innych miejsc. Krawędzie wypukłej otoczki wejścia są również krawędziami triangulacji Delaunaya, ale odpowiadają raczej promieniom niż segmentom liniowym diagramu Woronoja. Tę dwoistość między diagramami Woronoja a triangulacjami Delaunaya można przekształcić w dwoistość między grafami skończonymi na jeden z dwóch sposobów: dodając sztuczny wierzchołek w nieskończoności do diagramu Woronoja, który służy jako drugi punkt końcowy dla wszystkich jego promieni, lub traktując ograniczona część diagramu Woronoja jako słaba liczba podwójna triangulacji Delaunaya. Chociaż diagram Woronoja i triangulacja Delaunaya są dualne, ich osadzenie w płaszczyźnie może mieć dodatkowe przecięcia poza przecięciami podwójnych par krawędzi. Każdy wierzchołek trójkąta Delaunaya jest umieszczony na odpowiadającej mu ścianie diagramu Woronoja. Każdy wierzchołek diagramu Woronoja znajduje się w środku okręgu opisanego na odpowiednim trójkącie triangulacji Delaunaya, ale ten punkt może leżeć poza jego trójkątem.
Osadzenia niepłaskie
Pojęcie dualności można rozszerzyć na osadzanie wykresów na dwuwymiarowych rozmaitościach innych niż płaszczyzna. Definicja jest taka sama: istnieje podwójny wierzchołek dla każdego połączonego składnika dopełnienia wykresu w rozmaitości i podwójna krawędź dla każdej krawędzi grafu łączącej dwa podwójne wierzchołki po obu stronach krawędzi. W większości zastosowań tej koncepcji jest ona ograniczona do osadzania z właściwością, że każda ściana jest dyskiem topologicznym; to ograniczenie uogólnia wymaganie dla grafów planarnych, aby graf był połączony. Przy tym ograniczeniu liczba podwójna dowolnego wykresu osadzonego na powierzchni ma naturalne osadzenie na tej samej powierzchni, tak że liczba podwójna liczby podwójnej jest izomorficzna i izomorficznie osadzona w oryginalnym grafie. Na przykład pełny graf K 7 jest grafem toroidalnym : nie jest płaski, ale może być osadzony w torusie, przy czym każda ściana osadzania jest trójkątem. To osadzanie ma wykres Heawooda jako wykres podwójny.
Ta sama koncepcja sprawdza się równie dobrze w przypadku powierzchni nieorientowalnych . Na przykład K 6 można osadzić w płaszczyźnie rzutowej z dziesięcioma trójkątnymi ścianami jako hemi-dwudzieścian , którego dual jest grafem Petersena osadzonym jako hemi-dwudziestościan .
Nawet grafy planarne mogą mieć osadzenia niepłaskie, przy czym grafy podwójne pochodzą z tych osadzeń, które różnią się od ich płaskich podobieństw. Na przykład cztery wielokąty Petriego sześcianu (sześciokąty utworzone przez usunięcie dwóch przeciwległych wierzchołków sześcianu) tworzą sześciokątne ściany osadzenia sześcianu w torusie . Graf dualny tego zanurzenia ma cztery wierzchołki tworzące pełny graf K 4 z podwojonymi krawędziami. W osadzeniu torusa tego podwójnego wykresu sześć krawędzi incydentnych z każdym wierzchołkiem, w cyklicznej kolejności wokół tego wierzchołka, dwukrotnie przechodzi przez trzy pozostałe wierzchołki. W przeciwieństwie do sytuacji na płaszczyźnie, to osadzenie sześcianu i jego dwoistości nie jest czymś wyjątkowym; wykres sześcianu ma kilka innych osadzeń torusa, z różnymi liczbami podwójnymi.
Wiele równoważności między właściwościami grafów pierwotnych i dualnych grafów planarnych nie daje się uogólnić na niepłaskie grafy podwójne lub wymaga dodatkowej uwagi przy ich uogólnianiu.
Inną operacją na grafach osadzonych na powierzchni jest podwójna operacja Petriego , która wykorzystuje wielokąty Petriego osadzania jako powierzchnie nowego osadzania. W przeciwieństwie do zwykłego wykresu dualnego ma te same wierzchołki co graf oryginalny, ale generalnie leży na innej powierzchni. Dualizm powierzchniowy i dualność Petriego to dwie z sześciu operacji Wilsona i razem tworzą grupę tych operacji.
Matroidy i liczby podwójne algebraiczne
Podwójna algebraiczna spójnego grafu G jest grafem G * takim, że G i G * mają ten sam zestaw krawędzi, każdy cykl G jest przecięciem G * , a każde przecięcie G jest cyklem G * . Każdy graf planarny ma algebraiczną liczbę podwójną, która na ogół nie jest unikalna (wystarczy każda liczba podwójna zdefiniowana przez osadzenie płaszczyzny). Odwrotność jest w rzeczywistości prawdziwa, jak ustalił Hassler Whitney w kryterium planarności Whitneya :
- Spójny graf G jest planarny wtedy i tylko wtedy, gdy ma algebraiczną liczbę podwójną.
Ten sam fakt można wyrazić w teorii matroidów . Jeśli M jest matroidą graficzną grafu G , to graf G * jest algebraiczną liczbą podwójną G wtedy i tylko wtedy, gdy matroida graficzna G * jest matroidą dualną M . Następnie kryterium planarności Whitneya można przeformułować jako stwierdzające, że podwójna matroida graficznej matroidy M sama jest matroidem graficznym wtedy i tylko wtedy, gdy podstawowy graf G z M jest płaski. Jeśli G jest płaska, podwójna matroida jest graficzną matroidą podwójnego wykresu G . W szczególności wszystkie grafy dualne, dla wszystkich różnych płaskich osadzeń G , mają izomorficzne matroidy graficzne.
W przypadku osadzania powierzchni niepłaskich, w przeciwieństwie do grafów podwójnych planarnych, graf podwójny nie jest generalnie algebraicznym grafem podwójnym pierwotnego. A dla nieplanarnego grafu G , podwójna matroida graficznej matroidy G sama w sobie nie jest matroidem graficznym. Jednak nadal jest to matroid, którego obwody odpowiadają nacięciom w G iw tym sensie można go traktować jako kombinatorycznie uogólniony algebraiczny podwójny G .
Dualizm między grafami planarnymi eulerowskimi i dwudzielnymi można rozszerzyć na matroidy binarne (które obejmują matroidy graficzne pochodzące z grafów planarnych): matroid binarny jest eulerowski wtedy i tylko wtedy, gdy jego matroid podwójny jest dwudzielny .
Dwie dualne koncepcje obwodu i łączności krawędziowej są ujednolicone w teorii matroidów przez obwód matroidów : obwód graficznej matroidy płaskiego wykresu jest taki sam jak obwód grafu, a obwód podwójnej matroidy (graficzna matroida podwójnego graph) to łączność krawędzi grafu.
Aplikacje
Oprócz zastosowania w teorii grafów, dwoistość grafów planarnych ma zastosowanie w kilku innych obszarach badań matematycznych i obliczeniowych.
W systemach informacji geograficznej sieci przepływu (takie jak sieci pokazujące, jak woda przepływa w systemie strumieni i rzek) są dualne do sieci komórkowych opisujących podziały drenażu . Tę dwoistość można wyjaśnić modelując sieć przepływów jako drzewo rozpinające na wykresie siatki o odpowiedniej skali oraz modelując podział drenażu jako uzupełniające drzewo rozpinające grzbietów na wykresie z podwójną siatką.
W wizji komputerowej obrazy cyfrowe są podzielone na małe kwadratowe piksele , z których każdy ma swój własny kolor. Podwójny wykres tego podziału na kwadraty ma wierzchołek na piksel i krawędź między parami pikseli, które mają wspólną krawędź; jest to przydatne w zastosowaniach obejmujących grupowanie pikseli w połączone regiony o podobnych kolorach.
W geometrii obliczeniowej dwoistość między diagramami Woronoja a triangulacjami Delaunay implikuje, że każdy algorytm konstruowania diagramu Woronoja można natychmiast przekształcić w algorytm triangulacji Delaunay i odwrotnie. Ta sama dualność może być również wykorzystana w generowaniu siatki elementów skończonych . Algorytm Lloyda , metoda oparta na diagramach Voronoi do przesuwania zestawu punktów na powierzchni do bardziej równomiernie rozmieszczonych pozycji, jest powszechnie stosowana jako sposób na wygładzenie siatki elementów skończonych opisanej przez podwójną triangulację Delaunaya. Ta metoda poprawia siatkę, czyniąc jej trójkąty bardziej jednolitymi rozmiarami i kształtami.
W syntezie obwodów CMOS funkcja, która ma być zsyntetyzowana, jest reprezentowana jako wzór w algebrze Boole'a . Następnie ta formuła jest tłumaczona na dwa szeregowo-równoległe multigrafy . Wykresy te można interpretować jako schematy obwodów , w których krawędzie wykresów przedstawiają tranzystory bramkowane wejściami funkcji. Jeden obwód oblicza samą funkcję, a drugi jej uzupełnienie. Jeden z dwóch obwodów uzyskuje się przez przekształcenie koniunkcji i alternatyw formuły odpowiednio w szeregowe i równoległe kompozycje grafów. Drugi obwód odwraca tę konstrukcję, przekształcając koniunkcje i dysjunkcje formuły w równoległe i szeregowe kompozycje grafów. Te dwa obwody, powiększone o dodatkową krawędź łączącą wejście każdego obwodu z jego wyjściem, są planarnymi grafami dualnymi.
Historia
Dwoistość wypukłych wielościanów została uznana przez Johannesa Keplera w jego książce Harmonices Mundi z 1619 roku . Rozpoznawalne płaskie podwójne grafy, poza kontekstem wielościanów, pojawiły się już w 1725 roku w pośmiertnie opublikowanej pracy Pierre'a Varignona , Nouvelle Méchanique ou Statique . Było to jeszcze przed pracą Leonharda Eulera z 1736 r. na temat Siedmiu mostów w Królewcu , którą często uważa się za pierwszą pracę dotyczącą teorii grafów . Varignon przeanalizował siły działające na statyczne układy rozpórek , rysując wykres podwójny do rozpórek, z długościami krawędzi proporcjonalnymi do sił działających na rozpórki; ten podwójny wykres jest rodzajem diagramu Cremony . W związku z twierdzeniem o czterech kolorach , podwójne wykresy map (podziały płaszczyzny na regiony) zostały wspomniane przez Alfreda Kempe w 1879 r. I rozszerzone na mapy na niepłaskich powierzchniach przez Lothara Hefftera w 1891 r. Dualność jako operacja na abstrakcyjnych grafach planarnych została wprowadzona przez Hasslera Whitneya w 1931 roku.