Hemi-dwudziestościan
| Hemi-icosahedron | |
|---|---|
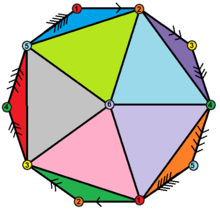 dziesięciokątny diagram Schlegla
| |
| Typ |
abstrakcyjny wielościan foremny globalnie rzutowy wielościan |
| Twarze | 10 trójkątów |
| Krawędzie | 15 |
| Wierzchołki | 6 |
| Konfiguracja wierzchołków | 3.3.3.3.3 |
| Symbol Schläfliego | {3,5}/2 lub {3,5} 5 |
| Grupa symetrii | A5 60 , zamów |
| Podwójny wielościan | hemi-dwunastościan |
| Nieruchomości |
nieorientowalna charakterystyka Eulera 1 |
Hemi -icosahedron to abstrakcyjny regularny wielościan zawierający połowę ścian regularnego dwudziestościanu . Można go zrealizować jako wielościan rzutowy ( teselacja rzeczywistej płaszczyzny rzutowej przez 10 trójkątów), który można zwizualizować, konstruując płaszczyznę rzutową jako półkulę, w której połączone są przeciwległe punkty wzdłuż granicy i dzieląc półkulę na trzy równe części.
Geometria
Ma 10 trójkątnych ścian, 15 krawędzi i 6 wierzchołków.
Jest to również związane z niewypukłym jednolitym wielościanem , tetrahemihexahedrem , który mógłby być topologicznie identyczny z hemi-icosahedrem, gdyby każdą z 3 kwadratowych ścian podzielono na dwa trójkąty.
Wykresy
Można to przedstawić symetrycznie na ścianach i wierzchołkach jako diagramy Schlegla :
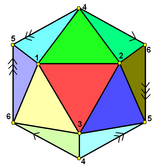
|
| Wyśrodkowany na twarz |
|---|
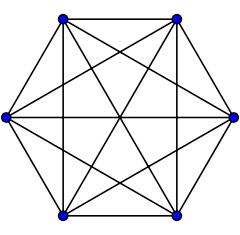
Pełny wykres K6
Ma te same wierzchołki i krawędzie, co 5-wymiarowy 5-simplex , który ma pełny wykres krawędzi, ale zawiera tylko połowę (20) ścian.
Z punktu widzenia teorii grafów jest to osadzenie ( pełnego wykresu na rzeczywistej rzutowej . Przy takim osadzeniu graf dualny jest grafem Petersena --- patrz hemi-dodecahedron .
Zobacz też
- 11-komorowy - abstrakcyjny regularny 4-polytop zbudowany z 11 hemi-icosahedra.
- hemi-dwunastościan
- półsześcian
- hemi-ośmiościan
- McMullen, Piotr ; Schulte, Egon (grudzień 2002), „6C. Projective Regular Polytopes”, Abstract Regular Polytopes (wyd. 1), Cambridge University Press, s. 162–165 , ISBN 0-521-81496-0
