Wykres Heawooda
| Wykres Heawooda | |
|---|---|
 | |
| Nazwany po | Percy'ego Johna Heawooda |
| Wierzchołki | 14 |
| Krawędzie | 21 |
| Promień | 3 |
| Średnica | 3 |
| Obwód | 6 |
| Automorfizmy | 336 ( PGL 2 (7) ) |
| Liczba chromatyczna | 2 |
| Indeks chromatyczny | 3 |
| Rodzaj | 1 |
| Grubość książki | 3 |
| Numer kolejki | 2 |
| Nieruchomości |
Dwudzielna klatka sześcienna przechodnia odległości regularna toroidalna hamiltonian symetryczna zorientowana prosto |
| Tabela wykresów i parametrów | |
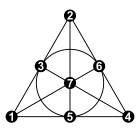
W matematycznej dziedzinie teorii grafów graf Heawooda jest grafem nieskierowanym z 14 wierzchołkami i 21 krawędziami, nazwany na cześć Percy'ego Johna Heawooda .
Właściwości kombinatoryczne
Wykres jest sześcienny , a wszystkie cykle na wykresie mają sześć lub więcej krawędzi. Każdy mniejszy graf sześcienny ma krótsze cykle, więc ten wykres jest 6- klatką , najmniejszym grafem sześciennym o obwodzie 6. Jest to graf przechodni na odległość (patrz spis Fostera ), a zatem regularny na odległość .
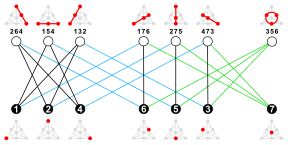
Na wykresie Heawooda znajdują się 24 doskonałe dopasowania ; dla każdego dopasowania zbiór krawędzi, które nie pasują, tworzy cykl Hamiltona . Na przykład rysunek pokazuje wierzchołki wykresu umieszczone na cyklu, przy czym wewnętrzne przekątne cyklu tworzą dopasowanie. Dzieląc krawędzie cyklu na dwa dopasowania, możemy podzielić wykres Heawooda na trzy idealne dopasowania (tj. 3-kolorowe jego krawędzie ) na osiem różnych sposobów. Każde dwa idealne dopasowania i każde dwa cykle Hamiltona można przekształcić w siebie przez symetrię grafu.
Na grafie Heawooda występuje 28 cykli z sześcioma wierzchołkami. Każdy 6-cykl jest rozłączny z dokładnie trzema innymi 6-cyklami; spośród tych trzech 6 cykli, każdy z nich jest symetryczną różnicą pozostałych dwóch. Wykres z jednym węzłem na 6 cykli i jedną krawędzią dla każdej rozłącznej pary 6 cykli to wykres Coxetera .
Właściwości geometryczne i topologiczne
Wykres Heawooda jest wykresem toroidalnym ; to znaczy, że można go osadzić bez przecinania na torusie . Jedno z tego typu osadzania umieszcza jego wierzchołki i krawędzie w trójwymiarowej przestrzeni euklidesowej jako zbiór wierzchołków i krawędzi niewypukłego wielościanu o topologii torusa, wielościanu Szilassiego .
Graf nosi imię Percy'ego Johna Heawooda , który w 1890 roku udowodnił, że w każdym podziale torusa na wielokąty regiony wielokątów można pokolorować co najwyżej siedmioma kolorami. Wykres Heawood tworzy podział torusa z siedmioma sąsiadującymi ze sobą regionami, pokazując, że ta granica jest ścisła.
Wykres Heawooda jest wykresem Leviego płaszczyzny Fano , wykresem przedstawiającym częstość występowania punktów i linii w tej geometrii. Przy tej interpretacji 6 cykli na wykresie Heawooda odpowiada trójkątom na płaszczyźnie Fano. Również graf Heawooda jest budową cycków grupy SL 3 (F 2 ) .
Wykres Heawooda ma numer przecięcia 3 i jest najmniejszym wykresem sześciennym z tym numerem przecięcia (sekwencja A110507 w OEIS ). Łącznie z wykresem Heawooda istnieje 8 różnych wykresów rzędu 14 z przecięciem numer 3.
Wykres Heawooda jest najmniejszym wykresem sześciennym z niezmiennikiem wykresu Colina de Verdière'a μ = 6.
Wykres Heawooda jest wykresem jednostkowej odległości : można go osadzić na płaszczyźnie w taki sposób, że sąsiednie wierzchołki są oddalone od siebie dokładnie o jeden, bez dwóch wierzchołków osadzonych w tym samym punkcie i bez wierzchołka osadzonego w punkcie w obrębie krawędzi.
Właściwości algebraiczne
Grupa automorfizmów grafu Heawooda jest izomorficzna z rzutową grupą liniową PGL 2 (7), grupą rzędu 336. Działa przechodnio na wierzchołkach, krawędziach i łukach grafu. Dlatego graf Heawooda jest grafem symetrycznym . Ma automorfizmy, które przenoszą dowolny wierzchołek do dowolnego innego wierzchołka i dowolną krawędź do dowolnej innej krawędzi. Co więcej, wykres Heawooda jest przechodni przez 4 łuki . Według spisu Fostera graf Heawooda, oznaczony jako F014A, jest jedynym sześciennym grafem symetrycznym na 14 wierzchołkach.
Ma grubość książki 3 i numer kolejki 2.
Charakterystyczny wielomian wykresu Heawooda to . Jest to jedyny wykres z tym charakterystycznym wielomianem, co czyni go wykresem określonym przez jego widmo.
Galeria
osadzony w torusie ( pokazany jako kwadrat )
osadzone w torusie (porównaj wideo )