Wykres Coxetera

Wykres Coxetera
Wykres Coxetera
	Wykres Coxetera
Nazwany po	HSM Coxeter
Wierzchołki	28
Krawędzie	42
Promień	4
Średnica	4
Obwód	7
Automorfizmy	336 ( PGL 2 (7))
Liczba chromatyczna	3
Indeks chromatyczny	3
Grubość książki	3
Numer kolejki	2
Nieruchomości	; ; Symetryczny hipohamiltonian sześcienny regularny odległości przechodni ; ;
	Tabela wykresów i parametrów

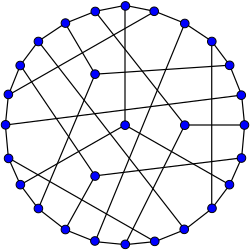
W matematycznej dziedzinie teorii grafów graf Coxetera jest 3- regularnym grafem z 28 wierzchołkami i 42 krawędziami. Jest to jeden z 13 znanych grafów regularnych odległości sześciennych . Jej nazwa pochodzi od Harolda Scotta MacDonalda Coxetera .

Nieruchomości

Graf Coxetera ma liczbę chromatyczną 3, indeks chromatyczny 3, promień 4, średnicę 4 i obwód 7. Jest to również graf spójny z 3 wierzchołkami i graf z 3 krawędziami . Ma grubość książki 3 i numer kolejki 2.

Graf Coxetera jest hipohamiltonowski : sam nie ma cyklu Hamiltona, ale każdy graf utworzony przez usunięcie z niego jednego wierzchołka jest hamiltonowski. Ma prostoliniowy numer przecięcia 11 i jest najmniejszym wykresem sześciennym z tym numerem przecięcia (sekwencja A110507 w OEIS ).

Budowa

Najprostsza konstrukcja wykresu Coxetera pochodzi z płaszczyzny Fano . Weź ⁷ C ₃ = 35 możliwych 3-kombinacji na 7 obiektach. Odrzuć 7 trójek odpowiadających liniom płaszczyzny Fano, pozostawiając 28 trójek. Połącz dwie trójki, jeśli są rozłączne. Wynikiem jest wykres Coxetera. (Patrz rysunek .) Ta konstrukcja pokazuje graf Coxetera jako indukowany podwykres wykresu Knesera $KG 7,3$ .

Wykres Coxetera można również zbudować z mniejszego wykresu Heawooda o regularnych odległościach , konstruując wierzchołek dla każdego 6-cyklu na grafie Heawooda i krawędź dla każdej rozłącznej pary 6-cykli.

Wykres Coxetera można wyprowadzić z wykresu Hoffmana-Singletona . Weź dowolny wierzchołek v w grafie Hoffmana-Singletona. Istnieje niezależny zestaw o rozmiarze 15, który zawiera v . Usuń 7 sąsiadów v i cały zbiór niezależny zawierający v , pozostawiając graf Coxetera.

Właściwości algebraiczne

Grupa automorfizmów grafu Coxetera jest grupą rzędu 336. Działa przechodnie na wierzchołkach, krawędziach i łukach grafu. Dlatego wykres Coxetera jest grafem symetrycznym . Ma automorfizmy, które przenoszą dowolny wierzchołek do dowolnego innego wierzchołka i dowolną krawędź do dowolnej innej krawędzi. Według spisu Fostera graf Coxetera, oznaczony jako F28A, jest jedynym sześciennym grafem symetrycznym na 28 wierzchołkach.

Wykres Coxetera jest również jednoznacznie określony przez widmo wykresu , zbiór wartości własnych wykresu jego macierzy sąsiedztwa .

Jako graf przechodni o skończonych połączonych wierzchołkach, który nie zawiera cyklu Hamiltona , wykres Coxetera jest kontrprzykładem dla wariantu hipotezy Lovásza , ale kanoniczne sformułowanie hipotezy wymaga ścieżki Hamiltona i jest weryfikowane przez wykres Coxetera.

Znanych jest tylko pięć przykładów grafów wierzchołkowo-przechodnich bez cykli Hamiltona: pełny graf K ₂ , graf Petersena , graf Coxetera i dwa grafy wyprowadzone z grafów Petersena i Coxetera przez zastąpienie każdego wierzchołka trójkątem.

Charakterystyczny wielomian wykresu Coxetera to ${\ Displaystyle (x-3) (x-2) ^ { 8}(x+1)^{7}(x^{2}+2x-1)^{6}}$ . Jest to jedyny wykres z tym charakterystycznym wielomianem, co czyni go wykresem określonym przez jego widmo.

Galeria

Układy

Są to różne reprezentacje wykresu Coxetera, używające tych samych etykiet wierzchołków. Istnieją cztery kolory i siedem wierzchołków każdego koloru. Każdy czerwony, zielony lub niebieski wierzchołek jest połączony z dwoma wierzchołkami tego samego koloru (cienkie krawędzie tworzące 7-cykle) i jednym białym wierzchołkiem (grube krawędzie).