Wykres jednostkowej odległości

Wykres jednostkowej odległości z 16 wierzchołkami i 40 krawędziami

W matematyce , w szczególności w teorii grafów geometrycznych , wykres odległości jednostkowej to wykres utworzony ze zbioru punktów na płaszczyźnie euklidesowej przez połączenie dwóch punktów, gdy odległość między nimi wynosi dokładnie jeden. Aby odróżnić te wykresy od szerszej definicji, która pozwala niektórym niesąsiadującym parom wierzchołków znajdować się w odległości jeden, można je również nazwać ścisłymi wykresami odległości jednostkowej lub wiernymi wykresami odległości jednostkowej . Jako dziedziczna rodzina grafów można je scharakteryzować zabronione indukowane podgrafy . Wykresy odległości jednostkowych obejmują wykresy kaktusowe , wykresy zapałek i wykresy groszowe oraz wykresy hipersześcianu . Uogólnione wykresy Petersena to nieścisłe wykresy odległości jednostkowych.

Nierozwiązany problem Paula Erdősa pyta, $wierzchołkach .$ może mieć wykres jednostkowej odległości na Najbardziej znana dolna granica jest nieco powyżej liniowej w $daleko$ od górnej granicy , proporcjonalnie do ${\ displaystyle n ^ {4/3}}$ . Nieznana jest również liczba kolorów wymaganych do pokolorowania wykresów odległości jednostkowych ( problem Hadwigera – Nelsona ): niektóre wykresy odległości jednostkowych wymagają pięciu kolorów, a każdy wykres odległości jednostkowych można pokolorować siedmioma kolorami. Dla każdej liczby algebraicznej istnieje wykres jednostkowej odległości z dwoma wierzchołkami, które muszą być oddalone od siebie o tę odległość. Zgodnie z twierdzeniem Beckmana – Quarlesa jedynymi przekształceniami płaszczyzny, które zachowują wszystkie wykresy odległości jednostkowych, są izometrie .

Możliwe jest wydajne skonstruowanie wykresu odległości jednostkowej, biorąc pod uwagę jego punkty. Znalezienie wszystkich odległości jednostkowych ma zastosowanie w dopasowywaniu wzorców , gdzie może być pierwszym krokiem w znalezieniu zgodnych kopii większych wzorców. Jednak ustalenie, czy dany wykres można przedstawić jako wykres jednostkowej odległości, jest NP-trudne , a dokładniej kompletne dla egzystencjalnej teorii liczb rzeczywistych .

Definicja

Wykres Petersena jako wykres jednostkowej odległości

Möbiusa – Kantora jako podwykres wykresu odległości jednostkowej

Wykres jednostkowej odległości dla zbioru punktów na płaszczyźnie jest grafem nieskierowanym , którego wierzchołkami są te punkty , z krawędzią między dwoma wierzchołkami, gdy ich odległość euklidesowa wynosi dokładnie jeden. O grafie abstrakcyjnym mówimy, że jest grafem odległości jednostkowych, jeśli możliwe jest znalezienie różnych położeń wierzchołków na płaszczyźnie, tak aby jego krawędzie miały długość jednostkową, a wszystkie niesąsiadujące pary wierzchołków miały odległości niejednostkowe. Gdy jest to możliwe, graf abstrakcyjny jest izomorficzny do wykresu jednostkowej odległości wybranych lokalizacji. Alternatywnie, niektóre źródła stosują szerszą definicję, pozwalając niesąsiadującym parom wierzchołków na odległość jednostkową. Otrzymane wykresy są podgrafami wykresów odległości jednostkowych (zgodnie z definicją tutaj). Tam, gdzie terminologia może być niejednoznaczna, grafy, w których krawędzie niebędące krawędziami muszą znajdować się w odległości niejednostkowej, można nazwać ścisłymi wykresami odległości jednostkowej lub wiernymi wykresami odległości jednostkowej . Podgrafy wykresów jednostkowych odległości są równoważnymi wykresami, które można narysować na płaszczyźnie przy użyciu tylko jednej długości krawędzi. Dla zwięzłości, ten artykuł odnosi się do nich jako do „nieścisłych wykresów odległości jednostkowych”.

Wykresów jednostkowych odległości nie należy mylić z wykresami dysków jednostkowych , które łączą pary punktów, gdy ich odległość jest mniejsza lub równa jeden, i są często używane do modelowania bezprzewodowych sieci komunikacyjnych.

Przykłady

Pełny graf na dwóch wierzchołkach jest wykresem odległości jednostkowej, podobnie jak pełny graf na trzech wierzchołkach ( wykres trójkątny ), ale nie pełny graf na czterech wierzchołkach. Uogólniając wykres trójkątny, każdy wykres cyklu jest wykresem jednostkowej odległości, realizowanym przez wielokąt foremny . Dwa wykresy odległości jednostek skończonych, połączone w jednym wspólnym wierzchołku, dają inny wykres odległości jednostkowych, ponieważ jeden z nich można obracać względem drugiego, aby uniknąć niepożądanych dodatkowych odległości jednostkowych. Łącząc w ten sposób grafy, każdy skończony drzewa lub kaktusa może być zrealizowany jako wykres jednostkowej odległości.

Wykres hipersześcianu ma 16 wierzchołków i 32 jednostkowe odległości ${\ displaystyle Q_ {4}}$

Wykres Hamminga ma 27 wierzchołków i 81 jednostkowych odległości ${\ Displaystyle H (3,3)}$

Każdy iloczyn kartezjański wykresów odległości jednostkowych daje inny wykres odległości jednostkowych; jednak to samo nie dotyczy niektórych innych popularnych produktów graficznych. Na przykład silny iloczyn grafów , zastosowany do dowolnych dwóch niepustych grafów, daje kompletne podgrafy z czterema wierzchołkami, które nie są grafami jednostkowej odległości. Iloczyny kartezjańskie grafów ścieżkowych tworzą grafy siatkowe o dowolnym wymiarze, iloczyny kartezjańskie pełnego grafu na dwóch wierzchołkach to grafy hipersześcianów , a iloczyny kartezjańskie grafów trójkątnych to grafy Hamminga ${\ Displaystyle H (d, 3)}$ .

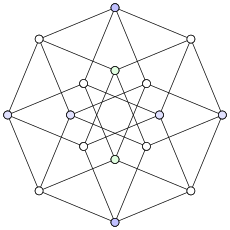
Inne specyficzne wykresy, które są wykresami odległości jednostkowych, obejmują wykres Petersena , wykres Heawooda , wykres koła (jedyny wykres koła, który jest wykresem odległości jednostkowej) oraz wykres wrzeciona Mosera i wykres Golomba ${\ Displaystyle W_ {7}}$ (małe 4- chromatyczne wykresy odległości). Wszystkie uogólnione wykresy Petersena , takie jak przedstawiony wykres Möbiusa – Kantora , są nieścisłymi wykresami odległości jednostkowych.

Wykresy zapałek to szczególny przypadek wykresów odległości jednostkowych, w których żadne krawędzie się nie przecinają. Każdy wykres zapałek jest grafem planarnym , ale niektóre inaczej płaskie wykresy odległości jednostkowych (takie jak wrzeciono Mosera) mają przecięcie w każdej reprezentacji jako wykres odległości jednostkowej. Ponadto w kontekście wykresów jednostkowych odległości termin „płaski” powinien być używany ostrożnie, ponieważ niektórzy autorzy używają go w odniesieniu do płaszczyzny, w której definiowane są odległości jednostkowe, a nie do zakazu przekraczania. Grafy groszowe są jeszcze bardziej szczególnym przypadkiem grafów jednostkowych odległości i zapałek, w których każda niesąsiadująca para wierzchołków jest oddalona od siebie o więcej niż jedną jednostkę.

Nieruchomości

Liczba krawędzi

Zobacz także: Problem różnych odległości Erdősa

Nierozwiązany problem z matematyki :

Ile jednostkowych odległości można określić za pomocą $punktów$ ?

(więcej nierozwiązanych problemów z matematyki)

Paul Erdős ( 1946 ) postawił problem oszacowania, ile par punktów w zbiorze $może$ znajdować się w jednostkowej odległości od siebie. Z punktu widzenia teorii grafów pytanie dotyczy tego, jak gęsty może być wykres jednostkowej odległości, a publikacja Erdősa na ten temat była jedną z pierwszych prac z zakresu teorii grafów ekstremalnych . Wykresy hipersześcianu i wykresy Hamminga zapewniają dolną granicę liczby jednostkowych odległości, proporcjonalną do ${\ Displaystyle n \ log n.}$ Rozważając punkty na kwadratowej siatce ze starannie dobranymi odstępami, Erdős znalazł ulepszoną dolną granicę formy

$${\ Displaystyle n ^ {1 + c / \ log \ log n}}$$

za stałą i zaoferował 500 $ za dowód, czy liczba jednostkowych odległości może być również ograniczona powyżej przez funkcję tej $.$ Najbardziej znaną górną granicą tego problemu jest

$${\ Displaystyle {\ sqrt [{3}] {\ Frac {29n ^ {4}} {4}}} \ około 1,936n ^ {4/3}.}$$

Ta granica może być postrzegana jako zliczanie przypadków między punktami i okręgami jednostkowymi i jest ściśle związana z nierównością liczbową przecięcia oraz z twierdzeniem Szemerédi-Trottera o częstościach między punktami i prostymi.

Dla małych wartości $do$ 14, stan na 2022 r.) znana jest dokładna maksymalna liczba możliwych krawędzi. Dla ${\ Displaystyle n = 2,3,4, \ kropki}$ te liczby krawędzi to:

1, 3, 5, 7, 9, 12, 14, 18, 20, 23, 27, 30, 33, ... (sekwencja A186705 w OEIS )

Zakazane subgrafy

Jeśli dany wykres $z$$G}$ nieścisłym wykresem odległości jednostkowej, nie jest nim też żaden supergraf sol $displaystyle$ . Podobny pomysł działa w przypadku grafów ścisłej odległości jednostkowej, ale przy użyciu koncepcji podgrafu indukowanego , podgrafu utworzonego ze wszystkich krawędzi między parami wierzchołków w danym podzbiorze wierzchołków. Jeśli nie jest ścisłym wykresem odległości jednostkowych, to nie jest nim żaden inny, $który$ ma $\ displaystyle G}$${\ Displaystyle G}$ jako wykres podrzędny indukowany. Ze względu na te relacje między tym, czy podgraf, czy jego supergraf jest wykresem jednostkowej odległości, możliwe jest opisanie wykresów jednostkowej odległości za pomocą ich zabronionych podgrafów . Są to grafy minimalne, które nie są grafami jednostkowej odległości danego typu. Można ich użyć do określenia, czy dany wykres $wykresem$ odległości jednostkowej dowolnego typu. ${\ displaystyle G}$ jest nieścisłym wykresem odległości jednostkowych wtedy i tylko wtedy, gdy ${\ displaystyle G}$ nie jest supergrafem zabronionego wykresu dla nieścisłych wykresów odległości jednostkowych. ${\ displaystyle G}$ jest ścisłym wykresem odległości jednostkowej wtedy i tylko wtedy, gdy nie jest indukowanym $supergrafem$ zabronionego wykresu dla ścisłych wykresów odległości jednostkowych

Zarówno w przypadku nieścisłych, jak i ścisłych wykresów odległości jednostkowych, wykresy zabronione obejmują zarówno pełny wykres, $}}$ 3 { $2,3$ . K. ${\ Displaystyle K_ {2,3}$ , wszędzie tam, gdzie umieszczone są wierzchołki po stronie dwóch wierzchołków tego wykresu, w odległości jednostkowej od nich znajdują się co najwyżej dwie pozycje, w których można umieścić pozostałe trzy wierzchołki, więc niemożliwe jest umieszczenie wszystkich trzech wierzchołków w różnych punktach. Są to jedyne dwa zabronione wykresy dla nieścisłych wykresów odległości jednostkowych na maksymalnie pięciu wierzchołkach; istnieje sześć zabronionych grafów na maksymalnie siedmiu wierzchołkach i 74 na grafach do dziewięciu wierzchołków. Ponieważ sklejenie dwóch wykresów odległości jednostkowych (lub ich podgrafów) w wierzchołku daje ścisłe (odpowiednio nieścisłe) wykresy odległości jednostkowych, każdy graf zabroniony jest grafem dwupołączonym , którego nie można uformować w tym procesie klejenia.

Wykres kołowy można zrealizować jako ścisły wykres odległości jednostkowej, w którym sześć jego wierzchołków tworzy jednostkowy $znajduje się$ , a siódmy w środku sześciokąta. Usunięcie jednej z krawędzi ze środkowego wierzchołka tworzy podgraf, który nadal ma krawędzie o jednostkowej długości, ale który nie jest ścisłym wykresem jednostkowej odległości. Umieszczenie jego wierzchołków w kształcie sześciokąta foremnego jest jedynym sposobem ( do kongruencji ) umieszczenia wierzchołków w różnych miejscach, tak aby sąsiednie wierzchołki były oddalone od siebie o jednostkę, a to umieszczenie również umieszcza dwa punkty końcowe brakującej krawędzi w odległości jednostkowej . Zatem jest to wykres zabroniony dla ścisłych wykresów odległości jednostkowych, ale nie jeden z sześciu zabronionych wykresów dla nieścisłych wykresów odległości jednostkowych. Inne przykłady wykresów, które nie są ścisłymi wykresami odległości jednostkowych, ale nie są ścisłymi wykresami odległości jednostkowych, obejmują wykres utworzony przez usunięcie zewnętrznej krawędzi z ${\ displaystyle W_ {7}}$ i wykres z sześcioma wierzchołkami utworzony z trójkątnego pryzmatu przez usunięcie krawędzi z jednego z jego trójkątów.

Liczby algebraiczne i sztywność

Główny artykuł: Twierdzenie Beckmana-Quarlesa

Dla każdej liczby algebraicznej $którym$ jest skonstruowanie wykresu odległości jednostkowej, $pewna$ para wierzchołków znajduje się w odległości we wszystkich $.$ odległości jednostkowej ${\ Displaystyle G}$ . Wynik ten implikuje skończoną wersję twierdzenia Beckmana – Quarlesa : dla dowolnych dwóch punktów $displaystyle$ w odległości $q}$${\ displaystyle \ alpha}$$}$ siebie istnieje skończony sztywny wykres odległości jednostkowej zawierający i $q$ taki, że każda transformacja płaszczyzny, która zachowuje jednostkowe odległości na tym wykresie, zachowuje również p {\ displaystyle odległość między ${\ displaystyle p}$ i ${\ displaystyle q}$ . Pełne twierdzenie Beckmana – Quarlesa stwierdza, że ​​​​jedynymi przekształceniami płaszczyzny euklidesowej (lub wielowymiarowej przestrzeni euklidesowej), które zachowują jednostkowe odległości, są izometrie . Równoważnie, dla wykresu nieskończonej odległości jednostkowej generowanego przez wszystkie punkty na płaszczyźnie, wszystkie automorfizmy grafu zachowują wszystkie odległości na płaszczyźnie, a nie tylko odległości jednostkowe.

Jeśli jest liczbą algebraiczną modułu $1$ , która nie jest pierwiastkiem jedności , to całkowite kombinacje potęg tworzą skończenie wygenerowaną podgrupę grupy addytywnej liczb zespolonych , których $\ displaystyle \ alpha}$ Wykres jednostkowej odległości ma stopień nieskończony . Na przykład można wybrać jeden z dwóch pierwiastków zespolonych wielomianu ${\ displaystyle \ alpha}$${\ Displaystyle z ^ {4} -z ^ {3} -z ^ {2} -z + 1}$ , tworząc nieskończony wykres odległości jednostkowej z czterema generatorami.

Kolorowanie

Główny artykuł: problem Hadwigera-Nelsona

Nierozwiązany problem z matematyki :

Jaka jest największa możliwa liczba chromatyczna wykresu odległości jednostkowej?

(więcej nierozwiązanych problemów z matematyki)

Hadwigera -Nelsona dotyczy liczby chromatycznej wykresów odległości jednostkowych, a dokładniej nieskończonego wykresu odległości jednostkowych utworzonego ze wszystkich punktów płaszczyzny euklidesowej. Zgodnie z twierdzeniem de Bruijna – Erdősa , które zakłada aksjomat wyboru , jest to równoznaczne z zapytaniem o największą liczbę chromatyczną wykresu odległości jednostek skończonych. Istnieją wykresy odległości jednostkowych wymagające pięciu kolorów w dowolnym odpowiednim kolorze, a wszystkie wykresy odległości jednostkowych można pokolorować co najwyżej siedmioma kolorami.

Siedmiokolorowy wykres nieskończonej odległości jednostkowej utworzony ze wszystkich punktów płaszczyzny oraz czterochromatyczne wrzeciono Mosera osadzone jako wykres odległości jednostkowej

Odpowiadając na inne pytanie Paula Erdősa, wykresy jednostek odległości bez trójkątów mogą wymagać czterech kolorów.

Wyliczenie

Liczba ścisłych wykresów odległości jednostkowych na wierzchołkach oznaczonych jako ${\ displaystyle n \ geq 4}$ wynosi co najwyżej

$${\ Displaystyle {\ binom {n (n-1)}} {2n}} = O \ left(2^{{\bigl (}4+o(1){\bigr )}n\log _{2}n}\right),}$$

wyrażone za pomocą notacji dużego O i notacji małego o.

Uogólnienie do wyższych wymiarów

Definicję wykresu odległości jednostkowej można oczywiście uogólnić na dowolną wielowymiarową przestrzeń euklidesową . W trzech wymiarach wykresy odległości jednostkowych punktów mają co najwyżej krawędzie, gdzie $n$${\ Displaystyle n ^ {3/2} \ beta$$} beta}$ jest bardzo wolno rosnącą funkcją związaną z funkcją odwrotną Ackermanna . Wynik ten prowadzi do podobnego ograniczenia liczby krawędzi trójwymiarowych względne grafy sąsiedztwa . W czterech lub więcej wymiarach każdy kompletny wykres dwudzielny jest wykresem jednostkowej odległości, realizowanym przez umieszczenie punktów na dwóch prostopadłych okręgach o wspólnym środku, więc wykresy jednostkowej odległości mogą być grafami gęstymi . Wzory wyliczeniowe dla wykresów odległości jednostkowych uogólniają się na wyższe wymiary i pokazują, że w wymiarach czterech lub więcej liczba ścisłych wykresów odległości jednostkowych jest znacznie większa niż liczba podgrafów wykresów odległości jednostkowych.

Dowolny wykres skończony może być osadzony jako wykres jednostkowej odległości w wystarczająco dużym wymiarze. Niektóre wykresy mogą wymagać bardzo różnych wymiarów osadzania, takich jak nieścisłe wykresy odległości jednostkowych i ścisłe wykresy odległości jednostkowych. Na przykład wykres korony wierzchołków $może$ być osadzony w czterech wymiarach jako nieścisły wykres odległości jednostkowej (to znaczy tak, że wszystkie jego krawędzie mają długość jednostkową Wymaga to jednak co najmniej ${\ displaystyle n-2}$ wymiary mają być osadzone jako ścisły wykres odległości jednostkowej, tak aby jego krawędzie były jedynymi parami jednostka-odległość. Wymiar potrzebny do zrealizowania dowolnego wykresu jako ścisłego wykresu jednostkowego jest co najwyżej dwukrotnością maksymalnego stopnia.

Złożoność obliczeniowa

Skonstruowanie wykresu odległości jednostkowej z jego punktów jest ważnym krokiem dla innych algorytmów znajdowania przystających kopii jakiegoś wzorca w większym zbiorze punktów. Algorytmy te wykorzystują tę konstrukcję do wyszukiwania pozycji kandydujących, w których występuje jedna z odległości we wzorcu, a następnie używają innych metod do testowania reszty wzorca dla każdego kandydata. metodę Matouška (1993) , uzyskując algorytm znajdowania wykresu jednostkowego odległości płaskiego zbioru punktów w czasie ${*} n)}}$$^$ gdzie jest wolno rosnącą iterowaną funkcją logarytmiczną .

Testowanie, czy dany wykres jest (ścisłym czy nieścisłym) jednostkowym wykresem odległości na płaszczyźnie, jest NP-trudne , a dokładniej kompletne dla egzystencjalnej teorii liczb rzeczywistych . Jest również NP-zupełne , aby określić, czy płaski wykres odległości jednostkowej ma cykl Hamiltona , nawet jeśli wszystkie wierzchołki wykresu mają znane współrzędne całkowite.

Źródła

•   Ágoston, Peter; Pálvölgyi, Dömötör (kwiecień 2022), „Ulepszony stały czynnik problemu jednostkowej odległości”, Studia Scientiarum Mathematicarum Hungarica , Akademiai Kiado Zrt., 59 (1): 40–57, arXiv : 2006.06285 , doi : 10.1556/012.2022.01517 , S2CID 218479287
•    Alon, Noga ; Kupavskii, Andrey (2014), „Dwa pojęcia wykresów odległości jednostkowych” (PDF) , Journal of Combinatorial Theory , Seria A, 125 : 1–17, doi : 10.1016 / j.jcta.2014.02.006 , MR 3207464 , S2CID 12043969
•    Beckman, FS; Quarles, DA, Jr. (1953), „O izometrii przestrzeni euklidesowych”, Proceedings of the American Mathematical Society , 4 (5): 810–815, doi : 10,2307/2032415 , JSTOR 2032415 , MR 0058193
•   Braß, Peter (2002), „Problemy geometrii kombinatorycznej w rozpoznawaniu wzorców”, Discrete & Computational Geometry , 28 (4): 495–510, doi : 10.1007 / s00454-002-2884-3 , MR 1949897
•    Brouwer, Andries E .; Haemers, Willem H. (2012), Spectra of Graphs , Universitext, Nowy Jork: Springer, s. 178, doi : 10.1007/978-1-4614-1939-6 , ISBN 978-1-4614-1938-9 , MR 2882891
•    Carmi, Paz; Dujmović, Vida ; Morin, Pat ; Wood, David R. (2008), „Wyraźne odległości na rysunkach grafów” , Electronic Journal of Combinatorics , 15 (1): Research Paper 107, arXiv : 0804,3690 , doi : 10,37236/831 , MR 2438579 , S2CID 2955082
•   Chan, Tymoteusz M .; Zheng, Da Wei (2022), „Problem Hopcrofta, golenie gwiazdy logarytmicznej, kaskadowanie ułamkowe 2d i drzewa decyzyjne”, w: Naor, Joseph (Seffi); Buchbinder, Niv (red.), Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, 9–12 stycznia 2022 r., Society for Industrial and Applied Mathematics, s. 190– 210, arXiv : 2111.03744 , doi : 10.1137/1.9781611977073.10 , S2CID 243847672
•   Chilakamarri, Kiran B. (1995), „4-chromatyczny wykres odległości jednostkowej bez trójkątów”, Geombinatorics , 4 (3): 64–76, MR 1313386
•   Chilakamarri, Kiran B.; Mahoney, Carolyn R. (1995), „Maksymalne i minimalne zabronione wykresy jednostkowo-odległościowe w płaszczyźnie”, Biuletyn Instytutu Kombinatoryki i Jego Zastosowań , 13 : 35–43, MR 1314500 , cyt. za Globus & Parshall (2020 )
•    Clarkson, Kenneth L .; Edelsbrunner, Herbert ; Guibas, Leonidas J .; Szarir, Michał ; Welzl, Emo (1990), „Kombinatoryczne granice złożoności dla układów krzywych i kul”, Discrete & Computational Geometry , 5 (2): 99–160, doi : 10.1007 / BF02187783 , MR 1032370 , S2CID 28143698
•   de Gray, Aubrey DNJ (2018), „Liczba chromatyczna samolotu wynosi co najmniej 5”, Geombinatorics , 28 : 5–18, arXiv : 1804,02385 , MR 3820926
•   Erdős, Paul (1946), „O $zbiorach$ odległości ” , American Mathematical Monthly , 53 (5): 248–250, doi : 10,2307/2305092 , JSTOR 2305092
•   Erdős, Paweł ; Harary, Frank ; Tutte, William T. (1965), „Na wymiar wykresu” (PDF) , Mathematika , 12 (2): 118–122, doi : 10,1112/S0025579300005222 , hdl : 2027,42/152495 , MR 0188096
• Erdős, Paweł ; Simonovits, Miklós (1980), „O liczbie chromatycznej grafów geometrycznych”, Ars Combinatoria , 9 : 229–246 , za Soifer (2008 , s. 97)
•    Erdős, Paul (1990), „Niektóre z moich ulubionych nierozwiązanych problemów”, w: Baker, A.; Bollobás, B.; Hajnal, A. (red.), Hołd dla Paula Erdősa , Cambridge University Press, s. 467–478, ISBN 0-521-38101-0 , MR 1117038 ; patrz w szczególności str. 475
• Gerbracht, Eberhard H.-A. (2009), Jedenaście jednostek odległości osadzania wykresu Heawooda , arXiv : 0912.5395 , Bibcode : 2009arXiv0912.5395G
• Gervacio, Severino V.; Lim, Yvette F.; Maehara , Hiroshi ( 2008 ) _ _
•   Globus, Aidan; Parshall, Hans (2020), „Małe wykresy jednostkowo-odległościowe w płaszczyźnie”, Biuletyn Instytutu Kombinatoryki i jej zastosowań , 90 : 107–138, arXiv : 1905.07829 , MR 4156400
•   Griffiths , Martin ( czerwiec 2019 ) _ _ _ _
•   Horwat, Borys; Pisanski, Tomaž (2010), „Iloczyny wykresów odległości jednostkowych”, Matematyka dyskretna , 310 (12): 1783–1792, doi : 10.1016/j.disc.2009.11.035 , MR 2610282
•    Huson, Mark L.; Sen, Arunabha (1995), „Algorytmy planowania transmisji dla sieci radiowych”, Military Communications Conference, IEEE MILCOM '95 , tom. 2, s. 647–651, doi : 10.1109/MILCOM.1995.483546 , ISBN 0-7803-2489-7 , S2CID 62039740
•    Itai, Alon; Papadimitriou, Christos H. ; Szwarcfiter, Jayme Luiz (1982), „Ścieżki Hamiltona w grafach siatki”, SIAM Journal on Computing , 11 (4): 676–686, CiteSeerX 10.1.1.383.1078 , doi : 10.1137/0211056 , MR 0677661
• Jaromczyk, Jerzy W.; Toussaint, Godfried T. (1992), „Względne wykresy sąsiedztwa i ich krewni”, Proceedings of the IEEE , 80 (9): 1502–1517, doi : 10.1109 / 5.163414
• Langin, Katie (18 kwietnia 2018), „Mateatyk-amator rozwiązuje problem matematyczny sprzed dziesięcioleci” , Nauka
•    Lavollée, Jérémy; Swanepoel, Konrad J. (2022), „Ograniczenie liczby krawędzi wykresów zapałek”, SIAM Journal on Discrete Mathematics , 36 (1): 777–785, arXiv : 2108,07522 , doi : 10,1137/21M1441134 , MR 4399020 , S2CID 237142 624
• Maehara, Hiroshi (1991), „Odległości na sztywnym wykresie jednostkowo-odległościowym w płaszczyźnie”, Discrete Applied Mathematics , 31 (2): 193–200, doi : 10,1016 / 0166-218X (91) 90070-D
•   Maehara, Hiroshi (1992), „Rozszerzanie elastycznej ramy jednostkowej do sztywnej”, Discrete Mathematics , 108 (1–3): 167–174, doi : 10.1016 / 0012-365X (92) 90671-2 , MR 1189840
•   Maehara, Hiroshi; Rödl, Vojtech (1990), „O wymiarze przedstawiającym wykres za pomocą wykresu odległości jednostkowej”, Graphs and Combinatoryics , 6 (4): 365–367, doi : 10.1007 / BF01787703 , S2CID 31148911
•   Matoušek, Jiří (1993), „Wyszukiwanie zakresu za pomocą wydajnych cięć hierarchicznych”, Discrete & Computational Geometry , 10 (2): 157–182, doi : 10.1007 / BF02573972 , MR 1220545
•   O'Donnell, Paul (1995), „A 40 wierzchołków 4-chromatycznych trójkątów bez jednostek odległości”, Geombinatorics , 5 (1): 31–34, MR 1337155
•    Pach, János ; Tardos, Gábor (2005), „Zakazane wzory i odległości jednostkowe”, w: Mitchell, Joseph SB; Rote, Günter (red.), Proceedings of the 21. ACM Symposium on Computational Geometry, Piza, Włochy, 6-8 czerwca 2005 r., Association for Computing Machinery, s. 1–9, doi : 10.1145/1064092.1064096 , MR 2460341 , S2CID 18752227
•    Radchenko, Danylo (2021), „Wykresy odległości jednostkowych i liczby całkowite algebraiczne”, Discrete & Computational Geometry , 66 (1): 269–272, doi : 10.1007/s00454-019-00152-4 , hdl : 21.11116/0000-0006- 9CFD-E , MR 4270642 , S2CID 119682489
•    Schaefer, Marcus (2013), „Realizacja wykresów i powiązań”, w: Pach, János (red.), Thirty Essays on Geometric Graph Theory , Springer, s. 461–482, CiteSeerX 10.1.1.220.9651 , doi : 10.1007/ 978-1-4614-0110-0_24 , ISBN 978-1-4614-0109-4
•   Soifer, Alexander (2008), The Mathematical Coloring Book , Springer-Verlag, ISBN 978-0-387-74640-1
•    Spencer, Joel ; Szemerédi, Endre ; Trotter, William T. (1984), „Odległości jednostkowe na płaszczyźnie euklidesowej”, w: Bollobás, Béla (red.), Graph Theory and Combinatorics , Londyn: Academic Press, s. 293–308, ISBN 978-0-12- 111760-3 , MR 0777185
•   Szemerédi, Endre (2016), „Problem odległości jednostkowej Erdősa”, w: Nash, John Forbes, Jr .; Rassias, Michael Th. (red.), Open Problems in Mathematics , Cham, Szwajcaria: Springer, s. 459–477, doi : 10.1007 / 978-3-319-32162-2_15 , MR 3526946
•    Tyszka, Apoloniusz (2000), „Dyskretne wersje twierdzenia Beckmana-Quarlesa”, Aequationes Mathematicae , 59 (1–2): 124–133, arXiv : math/9904047 , doi : 10.1007/PL00000119 , MR 1741475 , S2CID 148031 82
•    Wormald, Nicholas (1979), „4-chromatyczny wykres ze specjalnym rysunkiem płaszczyzny”, Journal of the Australian Mathematical Society , seria A, 28 (1): 1–8, doi : 10.1017 / S1446788700014865 , MR 0541161 , S2CID 124067465
•   Žitnik, Arjana; Horwat, Borys; Pisanski, Tomaž (2012), „Wszystkie uogólnione wykresy Petersena to wykresy jednostkowo-odległościowe”, Journal of the Korean Mathematical Society , 49 (3): 475–491, doi : 10.4134/JKMS.2012.49.3.475 , MR 2953031

Linki zewnętrzne

• Venkatasubramanian, Suresh, „Problem 39: Odległości między zbiorami punktów w R ² i R ³ ” , The Open Problems Project
• Weisstein, Eric W. , „Wykres jednostkowo-odległościowy” , MathWorld