Podwójny Petrie
W teorii grafów topologicznych podwójna Petrie grafu osadzonego ( na rozmaitości 2 z dyskami o wszystkich ścianach) jest kolejnym osadzonym grafem, którego ścianami są wielokąty Petriego z pierwszego osadzania.
Podwójny Petrie jest również nazywany Petrialem , a podwójny Petrie osadzonego wykresu może być oznaczony . Można to uzyskać z podpisanego systemu rotacji lub reprezentacji wykresu wstęgowego osadzania poprzez skręcenie każdej krawędzi osadzania.
Nieruchomości
Podobnie jak w przypadku zwykłego wykresu dualnego , dwukrotne powtórzenie podwójnej operacji Petriego powoduje powrót do pierwotnego osadzania powierzchni. W przeciwieństwie do zwykłego wykresu dualnego (który jest osadzeniem zasadniczo innego wykresu na tej samej powierzchni), dualny wykres Petriego jest osadzeniem tego samego wykresu na ogólnie innej powierzchni.
Dualizm powierzchniowy i dualność Petriego to dwie z sześciu operacji Wilsona i razem tworzą grupę tych operacji.
Regularne wielościany
Zastosowanie liczby podwójnej Petriego do regularnego wielościanu daje regularną mapę . Liczba skośnych h -gonalnych to g /2 h , gdzie g to kolejność grup , a h to liczba coxetera grupy.
Na przykład podwójny sześcian Petriego (wykres dwudzielny z ośmioma wierzchołkami i dwunastoma krawędziami osadzony na kuli o sześciu kwadratowych ścianach) ma cztery sześciokątne ściany, równiki sześcianu. Topologicznie tworzy osadzenie tego samego wykresu na torusie.
Regularne mapy otrzymane w ten sposób są następujące.
- Czworościan petrialny {3,3} π ma 4 wierzchołki, 6 krawędzi i 3 skośne ściany kwadratowe. Przy charakterystyce Eulera χ równej 1 jest on topologicznie identyczny z półsześcianem {4,3}/2 .
- Sześcian petriala {4,3} π ma 8 wierzchołków, 12 krawędzi i 4 skośne sześciokąty, tutaj w kolorze czerwonym, zielonym, niebieskim i pomarańczowym. Przy charakterystyce Eulera równej 0 można to również zobaczyć na czterech sześciokątnych powierzchniach sześciokątnej płytki jako typ {6,3} (2,0) .
- Ośmiościan petrialny {3,4} π ma 6 wierzchołków, 12 krawędzi i 4 skośne ściany sześciokątne. Ma charakterystykę Eulera -2 i ma odwzorowanie na porządek hiperboliczny - 4 heksagonalne kafelki , jako typ {6,4} 3 .
- Dwunastościan petrialny , {5,3} π , ma 20 wierzchołków, 30 krawędzi i 6 skośnych ścian dziesięciokątnych oraz charakterystykę Eulera -4, związaną z kafelkami hiperbolicznymi jako typu {10,3} 5 .
- Dwudziestościan petrialny , {3,5} π , ma 12 wierzchołków, 30 krawędzi i 6 skośnych ścian dziesięciokątnych oraz charakterystykę Eulera -12, związaną z kafelkami hiperbolicznymi jako typu {10,5} 3 .
| Nazwa |
Petrialny czworościan |
Kostka Petriala |
Petrialny ośmiościan |
dwunastościan Petriala |
Petrialny dwudziestościan |
|---|---|---|---|---|---|
| Symbol | {3,3} π , {4,3} 3 | {4,3} π , {6,3} 4 | {3,4} π , {6,4} 3 | {5,3} π , {10,3} | {3,5} π , {10,5} |
| (v,e,f), χ | (4,6,3), χ = 1 | (8,12,4), χ = 0 | (6,12,4), χ = −2 | (20,30,6), χ = −4 | (12,30,6), χ = −12 |
| Twarze | 3 skośne kwadraty
|
4 skośne sześciokąty | 6 skośnych dziesięciokątów | ||

|

|

|

|
||
| Animacja |

|

|

|

|

|
| obrazu |

|

|

|

|

|
|
Powiązane liczby |
 {4,3} 3 = {4,3}/2 = {4,3} (2,0) |
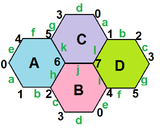 {6,3} 3 = {6,3} (2,0) |
 {6,4} 3 = {6,4} (4,0) |
{10,3} 5 | {10,5} 3 |
Istnieją również 4 petriały wielościanów Keplera – Poinsota :
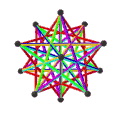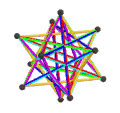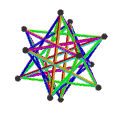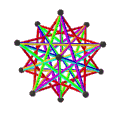
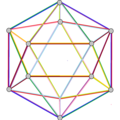
- Dwunastościan wielki petriala {5,5/2} π ma 12 wierzchołków, 30 krawędzi i 10 skośnych ścian sześciokątnych o charakterystyce Eulera χ wynoszącej -8.
- Petrial mały dwunastościan gwiaździsty , {5/2,5} π , ma 12 wierzchołków, 30 krawędzi i 10 skośnych ścian sześciokątnych o χ równym -8.
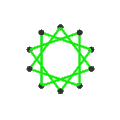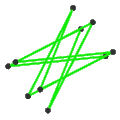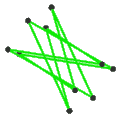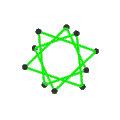
- Wielki dwudziestościan petrialny {3,5/2} π ma 12 wierzchołków, 30 krawędzi i 6 skośnych ścian dekagramowych o χ równym -12.
- Petrial wielki dwunastościan gwiaździsty , {5/2,3} π , ma 20 wierzchołków, 30 krawędzi i 6 skośnych ścian dekagramowych o χ równym -4.
| Nazwa |
Petrial wielki dwunastościan |
Petrial mały gwiaździsty dwunastościan |
Petrial wielki dwudziestościan |
Petrial wielki gwiaździsty dwunastościan |
|---|---|---|---|---|
| Symbol | {5,5/2} π , {6,5/2} | {5/2,5} π , {6,5} | {3,5/2} π , {10/3,5/2} | {5/2,3} π , {10/3,3} |
| (v,e,f), χ | (12,30,10), χ = -8 | (12,30,10), χ = -8 | (12,30,6), χ = -12 | (20,30,6), χ = -4 |
| Twarze | 10 skośnych sześciokątów | 6 skośnych dekagramów (jeden niebieski dekagram zarysowany) | ||

|

|

|
|
|
| Animacja |
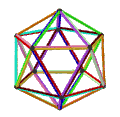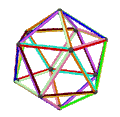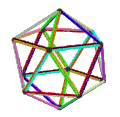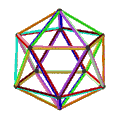
|
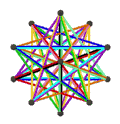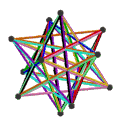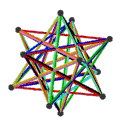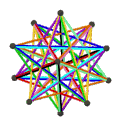
|
|

|
| obrazu |
|

|

|

|



