Twierdzenie Steinitza

Ten artykuł dotyczy twierdzenia o grafach wielościanów. W przypadku innych zastosowań zobacz twierdzenie Steinitza (ujednoznacznienie) .

W kombinatoryce wielościennej , gałęzi matematyki, twierdzenie Steinitza jest charakterystyką grafów nieskierowanych utworzonych przez krawędzie i wierzchołki trójwymiarowych wypukłych wielościanów : są to dokładnie grafy planarne połączone z 3 wierzchołkami . Oznacza to, że każdy wielościan wypukły tworzy 3-połączony graf planarny, a każdy 3-połączony graf planarny można przedstawić jako wykres wielościanu wypukłego. Z tego powodu 3-połączone grafy planarne są również znane jako grafy wielościenne .

Wynik ten dostarcza twierdzenia klasyfikacyjnego dla trójwymiarowych wypukłych wielościanów, czegoś, co nie jest znane w wyższych wymiarach. Zapewnia pełny i czysto kombinatoryczny opis wykresów tych wielościanów, umożliwiając łatwiejsze udowodnienie innych wyników na nich, takich jak twierdzenie Eberharda o realizacji wielościanów z zadanymi typami ścian, bez odniesienia do geometrii tych kształtów . Dodatkowo została zastosowana w rysowaniu wykresów , jako sposób konstruowania trójwymiarowych wizualizacji abstrakcyjnych wykresów. Branko Grünbaum nazwał to twierdzenie „najważniejszym i najgłębszym znanym wynikiem dotyczącym 3-polytopów ”.

Twierdzenie to pojawia się w publikacji Ernsta Steinitza z 1922 r ., od którego pochodzi jego nazwa. Można to udowodnić za pomocą indukcji matematycznej (tak jak zrobił to Steinitz), znajdując stan minimalnej energii dwuwymiarowego układu sprężynowego i podnosząc wynik do trzech wymiarów lub stosując twierdzenie o upakowaniu koła . Znanych jest kilka rozszerzeń twierdzenia, w których wielościan realizujący dany graf ma dodatkowe ograniczenia; na przykład każdy wykres wielościanu jest wykresem wielościanu wypukłego o współrzędnych całkowitych lub wykresem wielościanu wypukłego, którego wszystkie krawędzie są styczne do wspólnego środek kuli .

Definicje i stwierdzenie twierdzenia

Oświetlenie szkieletu wypukłego wielościanu ze źródła światła znajdującego się blisko jednej z jego ścian powoduje, że jego cienie tworzą planarny diagram Schlegla .

Graf nieskierowany to układ wierzchołków i krawędzi , z których każda łączy dwa wierzchołki. Jak to zwykle bywa w teorii grafów, dla celów twierdzenia Steinitza grafy te są ograniczone do skończonych (wierzchołki i krawędzie są zbiorami skończonymi ) i prostych (żadne dwie krawędzie nie łączą tych samych dwóch wierzchołków i żadna krawędź nie łączy wierzchołka ze sobą) . Z dowolnego wielościanu można utworzyć graf, pozwalając wierzchołkom wykresu odpowiadać wierzchołkom wielościanu i łącząc dowolne dwa wierzchołki grafu krawędzią, gdy odpowiadające dwa wierzchołki wielościanu są punktami końcowymi krawędzi wielościanu. Ten wykres jest znany jako szkielet wielościanu.

Graf jest planarny, jeśli można go narysować tak, aby jego wierzchołki były punktami na płaszczyźnie euklidesowej , a jego krawędzie były krzywymi łączącymi te punkty w taki sposób, że żadne dwie krzywe krawędzi nie przecinają się i tak, że punkt reprezentujący wierzchołek leży na krzywej reprezentujący krawędź tylko wtedy, gdy wierzchołek jest punktem końcowym krawędzi. Zgodnie z twierdzeniem Fáry'ego każdy płaski rysunek można wyprostować tak, aby krzywe reprezentujące krawędzie były odcinkami linii . Graf jest 3-spójny jeśli ma więcej niż trzy wierzchołki, a po usunięciu dowolnych dwóch wierzchołków każda inna para wierzchołków pozostaje połączona ścieżką. Twierdzenie Steinitza stwierdza, że ​​​​te dwa warunki są zarówno konieczne, jak i wystarczające do $\ displaystyle G}$ szkieletów trójwymiarowych wypukłych wielościanów: dany wykres jest wykresem wypukłego trójwymiarowego wielościanu wtedy i tylko wtedy, gdy $displaystyle G}$${$ jest planarny i połączony z 3 wierzchołkami.

Dowody

Ilustracja dowodu twierdzenia Balińskiego , przedstawiająca zbiór zerowy funkcji liniowej (kolor niebieski) przechodzący przez dwa dane wierzchołki (kolor żółty) oraz ścieżki metody simplex łączące pozostały wykres (kolor zielony)

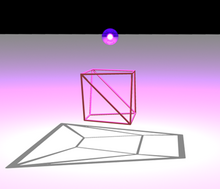
Jeden kierunek twierdzenia Steinitza (kierunek łatwiejszy do udowodnienia) mówi, że wykres każdego wypukłego wielościanu jest płaski i 3-spójny. Jak pokazano na ilustracji, planarność można pokazać za pomocą diagramu Schlegla : jeśli umieści się źródło światła w pobliżu jednej ściany wielościanu, a płaszczyznę po drugiej stronie, cienie krawędzi wielościanu utworzą planarny wykres, osadzony w taki sposób, aby krawędzie były odcinkami linii prostych. 3-łączność wykresu wielościennego jest szczególnym przypadkiem twierdzenia Balińskiego , że wykres dowolnego -wymiarowego ${\ displaystyle k}$$-połączona$ polytope jest . Łączność wykresu polytope, po usunięciu dowolnych $jego$$,$ , można udowodnić, wybierając jeszcze jeden wierzchołek liniową , wynosi zero na wynikowy zestaw $podążanie$ ścieżkami wygenerowanymi metodą simplex $.$ z jednym z dwóch skrajnych wierzchołków funkcji liniowej, przy czym wybrany wierzchołek jest połączony z obydwoma

Drugi, trudniejszy kierunek twierdzenia Steinitza mówi, że każdy planarny 3-połączony graf jest wykresem wielościanu wypukłego. Istnieją trzy standardowe podejścia do tej części: dowody przez indukcję, podnoszenie dwuwymiarowych osadzeń Tutte do trzech wymiarów przy użyciu korespondencji Maxwella-Cremony oraz metody wykorzystujące twierdzenie o upakowaniu koła w celu wygenerowania kanonicznego wielościanu .

Wprowadzenie

Transformaty Δ-Y i Y-Δ wielościanu

Chociaż oryginalny dowód Steinitza nie został wyrażony w kategoriach teorii grafów, można go przepisać w tych terminach i obejmuje znalezienie sekwencji transformacji Δ-Y i Y-Δ , które redukują dowolny 3-połączony graf planarny do ${\ displaystyle K_ {4}}$ , wykres czworościanu. Transformacja Y-Δ usuwa wierzchołek trzeciego stopnia z wykresu, dodając krawędzie między wszystkimi jego byłymi sąsiadami, jeśli te krawędzie jeszcze nie istniały; transformacja odwrotna, transformacja Δ-Y, usuwa krawędzie trójkąta z wykresu i zastępuje je nowym wierzchołkiem trzeciego stopnia sąsiadującym z tymi samymi trzema wierzchołkami. Po znalezieniu takiej sekwencji można ją odwrócić i przekształcić w operacje geometryczne, które krok po kroku budują pożądany wielościan, zaczynając od czworościanu. Każdą transformatę Y-Δ w odwróconej sekwencji można wykonać geometrycznie, wycinając wierzchołek trzeciego stopnia z wielościanu. Transformację Δ-Y w odwróconej kolejności można wykonać geometrycznie, usuwając trójkątną ścianę z wielościanu i wydłużając jej sąsiednie ściany do punktu, w którym się spotykają, ale tylko wtedy, gdy ten potrójny punkt przecięcia trzech sąsiednich ścian znajduje się po drugiej stronie usuniętej ściany z wielościanu. Kiedy potrójny punkt przecięcia nie znajduje się po drugiej stronie tej ściany, a przekształcenie rzutowe wielościanu wystarczy, aby przesunąć go na właściwą stronę. Dlatego przez indukcję liczby przekształceń Δ-Y i Y-Δ potrzebnych do zredukowania danego wykresu do $każdego$ można zrealizować jako wielościan.

$Δ$ , że ​​każdy wykres wielościenny można zredukować do przekształceń Δ-Y i Y- Epifanov udowodnił, że jeśli w grafie planarnym określone są dwa wierzchołki, to graf można zredukować do pojedynczej krawędzi między tymi terminalami, łącząc transformaty Δ-Y i Y-Δ z redukcjami szeregowo- równoległymi . Dowód Epifanowa był skomplikowany i niekonstruktywny, ale został uproszczony przez Truempera przy użyciu metod opartych na grafach drugorzędnych . Truemper zauważył, że każdy wykres siatki jest redukowalna przez Δ-Y i Y-Δ przekształca się w ten sposób, że ta redukowalność jest zachowana przez mniejsze grafy i że każdy graf planarny jest mniejszym grafu siatkowego. Pomysł ten można wykorzystać do zastąpienia lematu Steinitza, że ​​istnieje sekwencja redukcji. Po tym zastąpieniu resztę dowodu można przeprowadzić za pomocą indukcji w taki sam sposób, jak oryginalny dowód Steinitza. Dla tych dowodów, przeprowadzonych dowolnym sposobem znajdowania sekwencji przekształceń Δ-Y i Y-Δ, istnieją grafy wielościenne, które wymagają nieliniowej liczby kroków. Dokładniej, każdy graf planarny można zredukować za pomocą liczby kroków co najwyżej proporcjonalnych do ${\ Displaystyle n ^ {3/2}}$ i nieskończenie wiele wykresów wymaga liczby kroków co najmniej proporcjonalnej do ${\ Displaystyle n ^ {3/2}}$ , gdzie ${\ Displaystyle n}$ to liczba wierzchołków w grafie.

Alternatywna forma dowodu indukcyjnego polega na usunięciu krawędzi (i ściśnięciu wierzchołków stopnia drugiego, które mogą pozostać po tym usunięciu) lub skróceniu krawędzi i utworzeniu minora danego grafu planarnego. Dowolny wykres wielościenny można zredukować do $wykresu$ liczby tych operacji i ponownie operacje można odwrócić, a odwrócone operacje wykonać geometrycznie, dając wielościenną realizację Jednakże, chociaż łatwiej jest udowodnić, że istnieje sekwencja redukcji dla tego typu argumentów, a sekwencje redukcji są krótsze, kroki geometryczne potrzebne do odwrócenia sekwencji są bardziej skomplikowane.

Podnoszenie

Naprężenie równowagi na wykresie sześcianu

Ścięty rysunek podnoszący zestresowany rysunek (z tymi samymi pozycjami 2d) do 3d

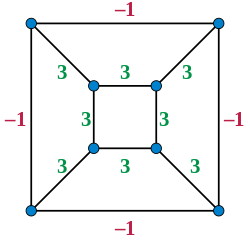
Jeśli wykres jest narysowany na płaszczyźnie o prostych krawędziach, to naprężenie równowagi definiuje się jako przypisanie krawędziom niezerowych liczb rzeczywistych (wag), z tą właściwością, że każdy wierzchołek znajduje się w pozycji określonej przez średnią ważoną jego sąsiedzi. Zgodnie z korespondencją Maxwella-Cremony, naprężenie równowagi można przenieść na odcinkowo liniową, ciągłą trójwymiarową powierzchnię, tak że krawędzie tworzące granice między płaskimi częściami powierzchni rzutują na dany rysunek. Waga i długość każdej krawędzi określa różnicę w nachyleniu powierzchni po obu stronach krawędzi, a warunek, że każdy wierzchołek jest w równowadze z sąsiadami, jest równoznaczny z warunkiem, że te różnice nachylenia powodują, że powierzchnia spotyka się ze sobą poprawnie w sąsiedztwie wierzchołka. Wagi dodatnie przekładają się na wypukłe kąty dwuścienne między dwiema ścianami odcinkowo liniowej powierzchni, a ujemne wagi przekładają się na wklęsłe kąty dwuścienne. I odwrotnie, każda ciągła odcinkowo-liniowa powierzchnia pochodzi w ten sposób z naprężenia równowagi. Jeśli narysowany zostanie skończony graf planarny i podane zostanie naprężenie równowagi w taki sposób, że wszystkie wewnętrzne krawędzie rysunku mają wagi dodatnie, a wszystkie krawędzie zewnętrzne mają wagi ujemne, to poprzez przełożenie tego naprężenia na trójwymiarową powierzchnię w ten sposób, a następnie zastępując płaską powierzchnię reprezentującą zewnętrzną stronę wykresu przez jej dopełnienie w tej samej płaszczyźnie, otrzymujemy wypukły wielościan, z dodatkową właściwością, że jego prostopadły rzut na płaszczyznę nie ma przecięć.

Korespondencja Maxwella-Cremony została wykorzystana do uzyskania wielościennych realizacji grafów wielościennych poprzez połączenie jej z metodą rysowania wykresów planarnych WT Tutte , osadzaniem Tutte . Metoda Tutte'a rozpoczyna się od ustalenia jednej ściany wykresu wielościennego w pozycji wypukłej w samolocie. Ta ściana stanie się zewnętrzną powierzchnią rysunku wykresu. Kontynuacją metody jest utworzenie układu równań liniowych we współrzędnych wierzchołków, zgodnie z którym każdy pozostały wierzchołek powinien być umieszczony na średniej swoich sąsiadów. Wtedy, jak pokazał Tutte, ten układ równań będzie miał unikalne rozwiązanie, w którym każda ściana grafu jest narysowana jako wielokąt wypukły. Intuicyjnie to rozwiązanie opisuje wzór, który można by uzyskać, zastępując wewnętrzne krawędzie wykresu idealnymi sprężynami i pozwalając im osiedlić się do ich stanu minimalnej energii. Rezultatem jest prawie naprężenie równowagi: jeśli przypiszemy wagę jednej każdej wewnętrznej krawędzi, to każdy wewnętrzny wierzchołek rysunku jest w równowadze. Jednak nie zawsze jest możliwe przypisanie liczb ujemnych zewnętrznym krawędziom, tak aby one również były w równowadze. Takie przypisanie jest zawsze możliwe, gdy zewnętrzna ściana jest trójkątem, więc tej metody można użyć do zrealizowania dowolnego wykresu wielościennego, który ma trójkątną ścianę. Jeśli graf wielościenny nie zawiera trójkątnej ściany, jego graf podwójny zawiera trójkąt i jest również wielościanem, więc można zrealizować dualność w ten sposób, a następnie zrealizować oryginalny wykres jako biegunowy wielościan realizacji dualnej. Alternatywna metoda realizacji wielościanów za pomocą podnoszenia pozwala uniknąć dwoistości, wybierając dowolną ścianę z co najwyżej pięcioma wierzchołkami jako ścianę zewnętrzną. Każdy graf wielościenny ma taką ścianę, a ostrożniej wybierając ustalony kształt tej ściany, można znieść osadzenie reszty wykresu w Tutte.

Pakowanie w kółko

Wielościan zrealizowany z koła upakującego się na niebieskiej środkowej kuli. Każdy wierzchołek wielościanu jest reprezentowany w upakowaniu przez jego koło horyzontu (czerwone). Każda twarz jest reprezentowana przez okrąg utworzony przez jej przecięcie z kulą.

Zgodnie z jednym z wariantów twierdzenia o upakowaniu okręgów , dla każdego grafu wielościennego istnieje układ okręgów na płaszczyźnie lub na dowolnej kuli, reprezentujących wierzchołki i ściany grafu, tak że:

• każde dwa sąsiednie wierzchołki grafu są reprezentowane przez styczne okręgi ,
• każde dwie sąsiednie ściany wykresu są reprezentowane przez styczne koło,
• każda para wierzchołków i ścian, z którymi się styka, jest reprezentowana przez okręgi przecinające się pod kątem prostym i
• wszystkie pozostałe pary kół są od siebie oddzielone.

Ten sam system okręgów tworzy reprezentację wykresu dualnego , zamieniając role okręgów reprezentujących wierzchołki i okręgów reprezentujących twarze. Z dowolnej takiej reprezentacji na kuli, osadzonej w trójwymiarowej przestrzeni euklidesowej, można utworzyć wypukły wielościan, który jest kombinatorycznie równoważny danemu wykresowi, jako przecięcie półprzestrzeni, których granice przechodzą przez okręgi twarzy . Z każdego wierzchołka tego wielościanu, horyzont na kuli, patrząc z tego wierzchołka, znajduje się koło, które ją reprezentuje. Ta właściwość horyzontu określa trójwymiarowe położenie każdego wierzchołka, a wielościan można równoważnie zdefiniować jako wypukłą otoczkę wierzchołków ustawionych w ten sposób. Kula staje się środkową kulą realizacji: każda krawędź wielościanu jest styczna do kuli w punkcie, w którym dwa styczne okręgi wierzchołków przecinają dwa styczne okręgi twarzy.

Realizacje z dodatkowymi właściwościami

Współrzędne całkowite

Można udowodnić silniejszą postać twierdzenia Steinitza, że ​​dowolny graf wielościenny może być zrealizowany przez wielościan wypukły, którego współrzędne są liczbami całkowitymi . Na przykład oryginalny dowód oparty na indukcji Steinitza można w ten sposób wzmocnić. Jednak liczby całkowite, które wynikałyby z konstrukcji Steinitza, są podwójnie wykładnicze pod względem liczby wierzchołków danego grafu wielościennego. Zapisywanie liczb tej wielkości w notacji binarnej wymagałoby wykładniczej liczby bitów. Z geometrycznego punktu widzenia oznacza to, że niektóre cechy wielościanu mogą mieć rozmiar dwukrotnie wykładniczo większy niż inne, co sprawia, że ​​​​realizacje wyprowadzone z tej metody są problematyczne w zastosowaniach w rysowaniu wykresów .

Kolejni badacze odkryli algorytmy realizacji oparte na podnoszeniu, które wykorzystują tylko liniową liczbę bitów na wierzchołek. Możliwe jest również $}$ wymogu, aby współrzędne były liczbami całkowitymi, i przypisanie współrzędnych w taki sposób, aby współrzędne wierzchołków były różnymi liczbami całkowitymi z zakresu od 0 do $2n-4}$${\ displaystyle x$ , a pozostałe dwie współrzędne są liczbami rzeczywistymi w przedziale jednostkowym , tak że każda krawędź ma długość co najmniej jeden, podczas gdy cały wielościan ma objętość liniową. Wiadomo, że niektóre grafy wielościenne są możliwe do zrealizowania na siatkach o wielkości tylko wielomianu; w szczególności dotyczy to piramid (realizacja wykresów kołowych ), pryzmatów (realizacja wykresów pryzmatycznych ) i ułożonych wielościanów (realizacja sieci apollińskich ).

Innym sposobem stwierdzenia istnienia realizacji liczb całkowitych jest to, że każdy trójwymiarowy wypukły wielościan ma kombinatorycznie równoważny wielościan całkowity. Na przykład dwunastościan foremny sam w sobie nie jest wielościanem całkowitym ze względu na swoje pięciokąty foremne, ale można go zrealizować jako równoważny pirytoedr całkowity . Nie zawsze jest to możliwe w wyższych wymiarach, gdzie istnieją polytopy (takie jak te zbudowane z konfiguracji Perlesa ), które nie mają odpowiednika w liczbach całkowitych.

Równe nachylenia

Graf Halina jest szczególnym przypadkiem grafu wielościennego utworzonego z drzewa osadzonego w płaszczyźnie (bez wierzchołków drugiego stopnia) przez połączenie liści drzewa w cykl . W przypadku grafów Halina można wybrać realizacje wielościenne specjalnego typu: cykl zewnętrzny tworzy poziomą wypukłą powierzchnię podstawy, a każda inna ściana leży bezpośrednio nad powierzchnią podstawy (jak w przypadku wielościanów realizowanych przez podnoszenie), przy czym wszystkie te górne ściany mający to samo nachylenie. Powierzchnie wielościenne o równych nachylonych powierzchniach nad dowolnym wielokątem bazowym (niekoniecznie wypukłym) można zbudować z wielokąta prosty szkielet , a równoważnym sposobem opisania tej realizacji jest to, że dwuwymiarowy rzut drzewa na ścianę podstawy tworzy jego prosty szkielet. Dowód tego wyniku wykorzystuje indukcję: każde ukorzenione drzewo można zredukować do mniejszego drzewa poprzez usunięcie liści z wewnętrznego węzła, którego wszystkie dzieci są liśćmi, wykres Halina utworzony z mniejszego drzewa ma realizację dzięki hipotezie indukcyjnej i tak jest można zmodyfikować tę realizację, aby dodać dowolną liczbę dzieci-liści do węzła drzewa, którego dzieci zostały usunięte.

Określanie kształtu twarzy

${\ displaystyle G }$ wielościanie, który reprezentuje dany wykres wielościenny $,$ ściany są dokładnie cyklami w $displaystyle G}$$\$ które nie dzielą na dwa składniki: to znaczy usunięcie cyklu twarzy $jako$$.$ resztę połączony podwykres Takie cykle nazywane są cyklami peryferyjnymi . Zatem kombinatoryczna struktura twarzy (ale nie ich kształty geometryczne) jest jednoznacznie określona na podstawie struktury grafu. Kolejne wzmocnienie twierdzenia Steinitza, dokonane przez Barnette'a i Grünbauma, stwierdza, że ​​dla dowolnego grafu wielościennego, dowolnej ściany grafu i dowolnego wielokąta wypukłego reprezentującego tę ścianę, można znaleźć wielościenną realizację całego grafu, która ma określony kształt dla wyznaczona twarz. Wiąże się to z twierdzeniem Tutte'a, że ​​dowolny graf wielościenny można narysować na płaszczyźnie ze wszystkimi ścianami wypukłymi i dowolnym określonym kształtem jego ściany zewnętrznej. Jednak planarne rysunki wykresów wytworzone metodą Tutte'a niekoniecznie podnoszą się do wypukłych wielościanów. Zamiast tego Barnette i Grünbaum dowodzą tego wyniku metodą indukcyjną. Zawsze jest też możliwe, biorąc pod uwagę wykres wielościenny $}$ dowolny $tworzy$ w , $aby$ znaleźć realizację, dla której sylwetkę sol $displaystyle C$ realizacja w rzucie równoległym .

Kule styczne

Realizacja wielościanów za pomocą twierdzenia o upakowaniu okręgu zapewnia kolejne wzmocnienie twierdzenia Steinitza: każdy 3-spójny płaski graf można przedstawić jako wypukły wielościan w taki sposób, że wszystkie jego krawędzie są styczne do tej samej sfery jednostkowej , środkowej kuli wielościan. Wykonując starannie wybraną transformację Möbiusa opakowania kołowego przed przekształceniem go w wielościan, możliwe jest znalezienie realizacji wielościennej, która realizuje wszystkie symetrie leżącego u podstaw wykresu, w tym sensie, że każdy automorfizm grafu jest symetrią realizacji wielościennej. Mówiąc $bardziej$ ogólnie, jeśli jest $wielościennym$ i dowolnym trójwymiarowym wypukłym ciałem , można znaleźć wielościenną reprezentację, w której wszystkie krawędzie są ${\ displaystyle G}$ styczna do ${\ displaystyle K}$ .

Metody pakowania w okręgi można również wykorzystać do scharakteryzowania wykresów wielościanów, które mają okrąg przechodzący przez wszystkie ich wierzchołki lub sferę styczną do wszystkich ich ścian. (Wielościany z okręgiem są również znaczące w geometrii hiperbolicznej jako idealne wielościany ). W obu przypadkach istnienie kuli jest równoważne z rozwiązywalnością układu nierówności liniowych na dodatnich zmiennych rzeczywistych związanych z każdą krawędzią wykresu. W przypadku sfery zmienne te muszą sumować się dokładnie do jednej w każdym cyklu twarzy na wykresie i do więcej niż jednej w każdym cyklu bez twarzy. Podwójnie, dla okręgu, zmienne muszą sumować się do jednej w każdym wierzchołku i więcej niż jednej w każdym cięciu z dwoma lub więcej wierzchołkami po każdej stronie cięcia. Chociaż może istnieć wykładniczo wiele nierówności liniowych do spełnienia, rozwiązanie (jeśli takie istnieje) można znaleźć w czasie wielomianowym przy użyciu metody elipsoidy . Wartości zmiennych z rozwiązania określają kąty między parami kół w upakowaniu kołowym, którego odpowiedni wielościan ma żądany stosunek do jego sfery.

Powiązane wyniki

Wykresy trójwymiarowych niewypukłych wielościanów mogą nie być połączone (po lewej), a nawet topologicznie kulistych wielościanów, których ściany są prostymi wielokątami, te wykresy mogą nie być połączone w 3 (po prawej).

W dowolnym wymiarze większym niż trzy algorytmiczny problem Steinitza polega na określeniu, czy dana krata jest siatką czołową wypukłego polytopu . Jest mało prawdopodobne, aby miał wielomianową złożoność czasową, ponieważ jest NP-trudny i silniej kompletny dla egzystencjalnej teorii liczb rzeczywistych , nawet dla czterowymiarowych politopów, zgodnie z twierdzeniem o uniwersalności Richtera-Geberta. Tutaj egzystencjalna teoria liczb rzeczywistych jest klasą problemów obliczeniowych, które można sformułować w kategoriach znajdowania zmiennych rzeczywistych, które spełniają dany układ równań i nierówności wielomianowych. W przypadku algorytmicznego problemu Steinitza zmiennymi takiego problemu mogą być współrzędne wierzchołków polytopu, a równania i nierówności mogą być użyte do określenia płaskości każdej ściany w danej sieci ścian i wypukłości każdego kąta między ścianami. Kompletność oznacza, że ​​każdy inny problem w tej klasie można przekształcić w równoważną instancję algorytmicznego problemu Steinitza w czasie wielomianowym. Istnienie takiej transformacji implikuje, że jeśli algorytmiczny problem Steinitza ma wielomianowe rozwiązanie czasowe, to tak samo ma każdy problem w egzystencjalnej teorii liczb rzeczywistych i każdy problem w NP. Ponieważ jednak dany wykres może odpowiadać więcej niż jednej sieci ścian, trudno jest rozszerzyć ten wynik kompletności na problem rozpoznawania wykresów 4-polytopów. Określenie złożoności obliczeniowej tego problemu rozpoznawania grafów pozostaje otwarte.

Naukowcy odkryli również teoretyczne charakterystyki grafów grafów niektórych specjalnych klas trójwymiarowych niewypukłych wielościanów i czterowymiarowych wypukłych wielościanów. Jednak w obu przypadkach ogólny problem pozostaje nierozwiązany. Rzeczywiście, nawet problem określenia, które kompletne wykresy są wykresami niewypukłych wielościanów (innych niż dla czworościanu i $Displaystyle$$K_ {7}}$ wielościanu Császár pozostaje nierozwiązany.

Twierdzenie Eberharda częściowo charakteryzuje wielozbiory wielokątów , które można łączyć, tworząc ściany wypukłego wielościanu. Można to udowodnić, tworząc 3-połączony graf planarny z danym zestawem ścian wielokątów, a następnie stosując twierdzenie Steinitza, aby znaleźć wielościenną realizację tego wykresu.

László Lovász wykazał zgodność między wielościennymi reprezentacjami grafów i macierzami realizującymi niezmienniki grafów Colina de Verdière'a tych samych grafów. Niezmiennik Colina de Verdière'a jest maksymalnym korkiem ważonej macierzy sąsiedztwa wykresu, pod pewnymi dodatkowymi warunkami, które są nieistotne dla grafów wielościennych. Są to kwadratowe symetryczne macierze $indeksowane$ przez wierzchołki, z wagą wierzchołka współczynniku przekątnej ${\ Displaystyle M_ {i, i}}$ i z wagą krawędzi ja $\ Displaystyle i, j}$ we współczynnikach poza przekątną ${\ Displaystyle M_ {i, j}}$ i ${\ displaystyle M_ {j, i}}$ . Gdy ${ \$ i nie sąsiadują ze sobą, współczynnik $}}$$j$ musi wynosić zero. Ten niezmiennik wynosi co najwyżej trzy wtedy i tylko wtedy, gdy graf jest grafem planarnym . Jak pokazuje Lovász, gdy wykres jest wielościenny, jego reprezentację jako wielościanu można uzyskać, znajdując ważoną macierz sąsiedztwa corank trzy, znajdując trzy wektory tworzące podstawę dla jego przestrzeni zerowej , używając współczynników tych wektorów jako współrzędnych dla wierzchołków wielościanu i odpowiednio skalując te wierzchołki.

Historia

Historię twierdzenia Steinitza opisuje Grünbaum (2007) , który odnotowuje jego pierwsze pojawienie się w tajemniczej formie w publikacji Ernsta Steinitza , pierwotnie napisanej w 1916 r. Steinitz podał więcej szczegółów w późniejszych notatkach z wykładów, opublikowanych po jego śmierci w 1928 r. Chociaż współczesne traktowanie twierdzenia Steinitza określa je jako teoretyczną charakterystykę wielościanów, Steinitz nie używał języka grafów. Sformułowanie twierdzenia oparte na teorii grafów zostało wprowadzone na początku lat 60. przez Branko Grünbauma i Theodore'a Motzkina , a jego dowód został również przekształcony w teorię grafów w tekście Grünbauma z 1967 r. Convex Polytopes . Praca Epifanowa nad transformacjami Δ-Y i Y-Δ, wzmacniająca dowód Steinitza, była motywowana innymi problemami niż charakterystyka wielościanów. Truemper (1989) przypisuje Grünbaumowi obserwację znaczenia tej pracy dla twierdzenia Steinitza.

Zgodność Maxwella-Cremony między diagramami naprężeń a podnoszeniem wielościennym została opracowana w serii artykułów Jamesa Clerka Maxwella w latach 1864-1870, na podstawie wcześniejszych prac Pierre'a Varignona , Williama Rankine'a i innych, i została spopularyzowana pod koniec XIX wieku przez Luigi Cremona . Obserwacja, że ​​ta zgodność może być wykorzystana z osadzeniem Tutte'a do udowodnienia twierdzenia Steinitza, pochodzi od Eadesa i Garvana (1995) .

Twierdzenie o upakowaniu okręgu zostało udowodnione przez Paula Koebe w 1936 r. I (niezależnie) przez EM Andreeva w 1970 r .; został spopularyzowany w połowie lat 80. przez Williama Thurstona , który (pomimo cytowania Koebe i Andreev) jest często uznawany za jednego z jego odkrywców. Wersja twierdzenia Andriejewa została już sformułowana jako charakterystyka podobna do Steinitza dla pewnych wielościanów w przestrzeni hiperbolicznej , a użycie pakowania kołowego do realizacji wielościanów ze środkowymi sferami pochodzi z pracy Thurstona. Problem charakteryzowania wielościanów z wpisanymi lub opisanymi sferami, ostatecznie rozwiązany metodą opartą na realizacjach pakowania kół, sięga niepublikowanej pracy René Descartesa około 1630 r. I Jakoba Steinera w 1832 r .; pierwsze przykłady wielościanów, które nie mają realizacji z okręgiem opisanym lub zamkniętym, podał Steinitz w 1928 roku.