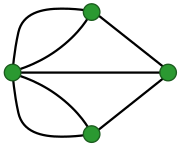
Lemat dotyczący uścisku dłoni

Na tym wykresie parzysta liczba wierzchołków (cztery wierzchołki o numerach 2, 4, 5 i 6) ma stopnie nieparzyste. Suma stopni wszystkich sześciu wierzchołków wynosi 2 + 3 + 2 + 3 + 3 + 1 = 14 , dwa razy więcej niż liczba krawędzi.

W teorii grafów , gałęzi matematyki, lemat uzgadniania jest stwierdzeniem, że w każdym skończonym grafie nieskierowanym liczba wierzchołków stykających się z nieparzystą liczbą krawędzi jest parzysta. Na przykład, jeśli jest grupa ludzi, którzy podają sobie ręce, liczba osób, które podają nieparzystą liczbę innych osób, jest parzysta. Lemat o uzgadnianiu jest konsekwencją wzoru na sumę stopni , zwanego też lematem o uzgadnianiu, zgodnie z którym suma stopni (liczba dotknięć każdego wierzchołka) jest równa dwukrotności liczby krawędzi grafu. Oba wyniki zostały udowodnione przez Leonharda Eulera ( 1736 ) w jego słynnym artykule o Siedmiu Mostach w Królewcu , który zapoczątkował badanie teorii grafów.

Poza problemem Siedmiu Mostów Królewca, który następnie sformalizował Eulera Tours , inne zastosowania formuły sumy stopni obejmują dowody pewnych struktur kombinatorycznych. Na przykład w dowodach lematu Spernera i problemu wspinaczki górskiej często pojawiają się geometryczne właściwości wzoru. Klasa złożoności PPA obejmuje trudność znalezienia drugiego nieparzystego wierzchołka, biorąc pod uwagę jeden taki wierzchołek w dużym niejawnie zdefiniowanym grafie .

Definicje i stwierdzenie

Graf nieskierowany składa się z układu wierzchołków i krawędzi łączących nieuporządkowane pary wierzchołków. Na każdym wykresie stopień $końcowym$ liczba krawędzi, których punktem jest $\$$v$ Dla wykresów, które mogą zawierać pętle łącząc wierzchołek ze sobą, pętla powinna być liczona jako wnosząca dwie jednostki do stopnia jej punktu końcowego dla celów lematu uzgadniania. Następnie $dotyczący uzgadniania stwierdza$ istnieć parzysta liczba wierzchołków, dla których liczbą nieparzystą Wierzchołki nieparzystego stopnia w grafie są czasami nazywane nieparzystymi węzłami (lub nieparzystymi wierzchołkami ); w tej terminologii lemat o uzgadnianiu można przeformułować jako stwierdzenie, że każdy wykres ma parzystą liczbę nieparzystych węzłów.

Formuła sumy stopni stwierdza, że

$$\ Displaystyle \ suma _ {v \ w V} \ stopień v = 2 | E |,}$$

gdzie to zbiór węzłów (lub wierzchołków) na wykresie, a $wykresie$$zbiór$ krawędzi na Oznacza to, że suma stopni wierzchołków równa się dwukrotności liczby krawędzi. W grafach skierowanych inna postać formuły sumy stopni stwierdza, że ​​suma stopni wejściowych wszystkich wierzchołków i suma stopni zewnętrznych są równe liczbie krawędzi. Tutaj stopień wejściowy to liczba krawędzi przychodzących, a stopień wyjściowy to liczba krawędzi wychodzących. Wersja formuły sumy stopni ma również zastosowanie do skończonych rodzin zbiorów lub równoważnie multigrafy : suma stopni elementów (gdzie stopień jest równy liczbie zawierających go zestawów) zawsze jest równa sumie liczności zbiorów .

Oba wyniki odnoszą się również do dowolnego podgrafu danego grafu, aw szczególności do jego spójnych składowych . Konsekwencją jest to, że dla każdego nieparzystego wierzchołka musi istnieć ścieżka łącząca go z innym nieparzystym wierzchołkiem.

Aplikacje

Ścieżki Eulera i wycieczki

Schematyczny widok siedmiu mostów Królewca

Wykres z wierzchołkami dla każdej masy lądowej i krawędzią dla każdego mostu

Leonhard Euler po raz pierwszy udowodnił lemat dotyczący uścisku dłoni w swojej pracy na temat Siedmiu mostów w Królewcu , prosząc o pieszą wycieczkę po Królewcu (obecnie Kaliningrad ), przechodząc przez każdy z siedmiu mostów raz. Można to przetłumaczyć na terminy teorii grafów jako prośbę o ścieżkę Eulera lub wycieczkę Eulera po połączonym grafie reprezentującym miasto i jego mosty: spacer przez wykres, który przechodzi przez każdą krawędź raz, kończąc się w innym wierzchołku niż zaczyna się w przypadku ścieżki Eulera lub wracając do punktu początkowego w przypadku trasy Eulera. Euler przedstawił podstawowe wyniki tego problemu w postaci liczby nieparzystych wierzchołków na grafie, które lemat o uzgadnianiu ogranicza do liczby parzystej. Jeśli ta liczba wynosi zero, istnieje trasa Eulera, a jeśli wynosi dwa, istnieje ścieżka Eulera. W przeciwnym razie problemu nie da się rozwiązać. W przypadku Siedmiu Mostów Królewca graf reprezentujący problem ma cztery nieparzyste wierzchołki i nie ma ani ścieżki Eulera, ani trasy Eulera. Niemożliwe było zatem zwiedzenie wszystkich siedmiu mostów w Królewcu bez powtórzenia jednego mostu.

W algorytmie Christofidesa-Serdyukova do aproksymacji problemu komiwojażera geometryczne implikacje formuły sumy stopni odgrywają istotną rolę, umożliwiając algorytmowi łączenie wierzchołków parami w celu skonstruowania wykresu, na którym trasa Eulera tworzy przybliżoną trasę TSP .

Wyliczanie kombinatoryczne

Można wykazać, że kilka struktur kombinatorycznych jest parzystych, odnosząc je do nieparzystych wierzchołków na odpowiednim „grafie wymiany”.

Na przykład, jak $w$ CAB Smith , każdym grafie sześciennym $musi$ istnieć parzysta liczba cykli Hamiltona przez dowolną ; są to cykle, które przechodzą przez każdy wierzchołek dokładnie raz. Thomason (1978) użył dowodu opartego na lemacie uzgadniania, aby rozszerzyć ten wynik na grafy, w których wszystkie wierzchołki mają nieparzysty stopień. Thomason definiuje wykres wymiany , H. $\ displaystyle H}$$są$$.$ relacji jeden do jednego ze ścieżkami Hamiltona $zaczynając$ od przechodząc przez $displaystyle$ ścieżki i są zdefiniowane jako połączone krawędzią w $H}$ , jeśli można uzyskać $displaystyle p_ {1}} 2}}$${\ displaystyle p_ {2}} p$ dodając nową krawędź na końcu i $}$ kolejną krawędź ze środka ${1}$ \ displaystyle p_ Ta operacja jest odwracalna, tworząc $.$ symetryczną , więc jest wykresem nieskierowanym Jeśli ścieżka ${$ się na wierzchołku $displaystyle$ to wierzchołek odpowiadający $p}$ w $\ displaystyle H}$ ma stopień równy liczbie sposobów, na jakie można wydłużyć o krawędź, która nie łączy się z powrotem; $displaystyle p}$${$ ; to znaczy stopień tego wierzchołka w $($ albo $w) -1}$ (liczba parzysta), jeśli nie tworzy się ${\ displaystyle p}$ cyklu $deg$ lub _ $(w) -2}$$uv}$ (liczba nieparzysta), jeśli jest częścią cyklu Hamiltona przez $Displaystyle$ . Ponieważ ma parzystą liczbę nieparzystych wierzchołków, musi mieć parzystą liczbę cykli Hamiltona przez $u$$displaystyle$$uv$ .

Inne aplikacje

Lemat dotyczący uzgadniania (lub formuła sumy stopni) jest również używany w dowodach kilku innych wyników w matematyce. Należą do nich:

Kolorowanie Spernera trójkątnego trójkąta, cieniowane w celu podkreślenia trzech małych trójkątów, które mają wszystkie trzy kolory wierzchołków

• Lemat Spernera mówi, że jeśli duży trójkąt jest podzielony na mniejsze trójkąty stykające się krawędziami, a wierzchołki są oznaczone trzema kolorami, tak że wzdłuż każdej krawędzi dużego trójkąta używane są tylko dwa kolory, to co najmniej jeden z mniejszych trójkątów ma wierzchołki wszystkich trzech kolorów; ma zastosowania w twierdzeniach o punkcie stałym , algorytmach wyszukiwania pierwiastków i dzieleniu sprawiedliwym . Jednym z dowodów tego lematu jest graf wymiany, którego wierzchołkami są trójkąty (zarówno małe, jak i duże) i którego krawędzie łączą pary trójkątów, które mają dwa wierzchołki o określonych dwóch kolorach. Duży trójkąt z konieczności ma nieparzysty stopień na tym wykresie wymiany, podobnie jak mały trójkąt ze wszystkimi trzema kolorami, ale nie inne małe trójkąty. Zgodnie z lematem dotyczącym uzgadniania musi istnieć nieparzysta liczba małych trójkątów ze wszystkimi trzema kolorami, a zatem musi istnieć co najmniej jeden taki trójkąt.

Problem wspinaczki górskiej

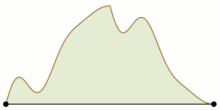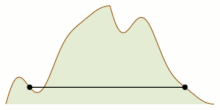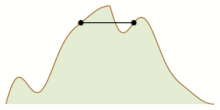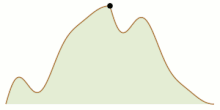
• Problem wspinaczki górskiej polega na tym, że dla wystarczająco dobrze zachowanych funkcji na jednostkowym przedziale , z równymi wartościami na końcach tego przedziału, możliwe jest skoordynowanie ruchu dwóch punktów, zaczynając od przeciwległych końców tego przedziału, tak aby spotykają się gdzieś pośrodku, pozostając w punktach o równej wartości przez cały ruch. Jednym z dowodów na to jest przybliżenie funkcji przez fragmentaryczną funkcję liniową z tymi samymi skrajnymi punktami, parametryzację położenia dwóch ruchomych punktów za pomocą współrzędnych pojedynczego punktu w kwadracie jednostkowym i pokazując, że dostępne pozycje dla dwóch punktów tworzą skończony wykres osadzony w tym kwadracie, z tylko pozycją początkową i jej odwróceniem jako nieparzystymi wierzchołkami. Zgodnie z lematem o uzgadnianiu te dwie pozycje należą do tego samego połączonego elementu grafu, a ścieżka z jednej do drugiej koniecznie przechodzi przez żądany punkt spotkania.
• Hipoteza rekonstrukcji dotyczy problemu jednoznacznego określenia struktury grafu z multizbioru podgrafów utworzonego przez usunięcie z niego pojedynczego wierzchołka. Biorąc pod uwagę te informacje, wzór na sumę stopni można wykorzystać do odzyskania liczby krawędzi w danym grafie i stopni każdego wierzchołka. Na tej podstawie można określić, czy dany graf jest grafem regularnym , a jeśli tak, określić go jednoznacznie na podstawie dowolnego podgrafu z usuniętymi wierzchołkami, dodając nowego sąsiada dla wszystkich wierzchołków podgrafu o zbyt niskim stopniu. Dlatego wszystkie grafy regularne można zrekonstruować.
• Gra Hex jest rozgrywana przez dwóch graczy, którzy umieszczają elementy swojego koloru na kafelku planszy w kształcie równoległoboku za pomocą sześciokątów dopóki jeden gracz nie będzie miał połączonej ścieżki sąsiednich elementów z jednej strony planszy na drugą. To nigdy nie może zakończyć się remisem: zanim plansza zostanie całkowicie wypełniona pionkami, jeden z graczy utworzy zwycięską ścieżkę. Jednym z dowodów na to jest wykres z wypełnionej planszy, z wierzchołkami w rogach sześciokątów i krawędziami po bokach sześciokątów, które oddzielają kolory dwóch graczy. Ten wykres ma cztery nieparzyste wierzchołki w rogach planszy, a nawet wierzchołki w innych miejscach, więc musi zawierać ścieżkę łączącą dwa rogi, która koniecznie ma zwycięską ścieżkę dla jednego gracza po jednej ze swoich stron.

Dowód

$sumy$$}$ wykorzystuje technikę podwójnego liczenia : liczy liczbę par incydentów, gdzie jest ${\ Displaystyle$ wierzchołkiem $displaystyle v}$ jest jednym z jego punktów końcowych na dwa różne sposoby. Wierzchołek należy do par ${\ Displaystyle \ deg (v)$$v$ gdzie ${\ Displaystyle \ deg (v)}$$)$ stopień to liczba krawędzi z nim związanych. Dlatego liczba par incydentów jest sumą stopni. Jednak każda krawędź na wykresie należy do dokładnie dwóch par incydentów, po jednej dla każdego z jego punktów końcowych; dlatego liczba par incydentów wynosi ${\ Displaystyle 2 | E |}$ . Ponieważ te dwie formuły liczą ten sam zestaw obiektów, muszą mieć równe wartości. Ten sam dowód można zinterpretować jako sumowanie wpisów macierzy częstości wykresu na dwa sposoby: wierszami, aby uzyskać sumę stopni, i kolumnami, aby uzyskać podwójną liczbę krawędzi.

W przypadku wykresów lemat dotyczący uzgadniania następuje jako następstwo wzoru na sumę stopni. W sumie liczb całkowitych na parzystość sumy nie mają wpływu parzyste wyrazy sumy; ogólna suma jest parzysta, gdy występuje parzysta liczba wyrazów nieparzystych, a nieparzysta, gdy występuje nieparzysta liczba wyrazów. Ponieważ jedna strona formuły sumy stopni to liczba parzysta ${\ Displaystyle 2 | E |}$ suma po drugiej stronie musi mieć parzystą liczbę wyrazów nieparzystych; to znaczy musi istnieć parzysta liczba wierzchołków nieparzystego stopnia.

Alternatywnie, możliwe jest użycie indukcji matematycznej , aby udowodnić wzór na sumę stopni lub bezpośrednio udowodnić, że liczba wierzchołków nieparzystych stopni jest parzysta, usuwając po jednej krawędzi z danego wykresu i stosując analizę przypadków na stopniach jego punktów końcowych, aby określić wpływ tego usunięcia na parzystość liczby wierzchołków nieparzystego stopnia.

W specjalnych klasach grafów

Graf Clebscha , regularny stopnia piątego, ma parzystą liczbę wierzchołków (16) i liczbę krawędzi (40), która jest wielokrotnością pięciu.

Rombowy dwunastościan jest dwuregularny z sześcioma wierzchołkami stopnia czwartego i ośmioma wierzchołkami stopnia trzeciego; 6 × 4 = 8 × 3 = 24 , jego liczba krawędzi.

Regularne wykresy

Formuła $wierzchołkami$$wykres$ , że $-$ regularny z ma Ponieważ liczba krawędzi musi być liczbą całkowitą, wynika z tego, że gdy $nieparzysta,$ liczba wierzchołków musi być parzysta. Dodatkowo, dla nieparzystych wartości liczba \ $displaystyle$ krawędzi musi być podzielna przez $r}$ .

Grafy dwudzielne i dwuregularne

Graf dwudzielny ma wierzchołki podzielone na dwa podzbiory, przy czym każda krawędź ma jeden punkt końcowy w każdym podzbiorze. Z tego samego argumentu podwójnego liczenia wynika, że ​​w każdym podzbiorze suma stopni jest równa liczbie krawędzi na wykresie. W szczególności oba podzbiory mają równe sumy stopni. Dla grafów dwuregularnych z podziałem wierzchołków na podzbiory i ${\$$displaystyle V_ {2}}$ z każdym wierzchołkiem w podzbiorze mającym $}}$ { stopień ${\ displaystyle r_ {i}}$ musi być tak, że ${\ Displaystyle | V_ {1} | r_ {1} = | V_ {2} | r_ {2}}$ ; oba są równe liczbie krawędzi.

Nieskończone wykresy

Graf nieskończony z tylko jednym nieparzystym wierzchołkiem

Lemat o uzgadnianiu nie ma zastosowania w swojej zwykłej postaci do grafów nieskończonych, nawet jeśli mają one tylko skończoną liczbę wierzchołków nieparzystych stopni. Na przykład nieskończony wykres ścieżkowy z jednym punktem końcowym ma tylko jeden wierzchołek nieparzystego stopnia, zamiast parzystej liczby takich wierzchołków. Możliwe jest jednak sformułowanie wersji lematu o uścisku dłoni przy użyciu pojęcia końca , klasa równoważności półnieskończonych ścieżek („promieni”) uznająca dwa promienie za równoważne, gdy istnieje trzeci promień, który wykorzystuje nieskończenie wiele wierzchołków z każdego z nich. Stopień końca to maksymalna liczba promieni rozłącznych krawędzi, które zawiera, a koniec jest nieparzysty, jeśli jego stopień jest skończony i nieparzysty. Mówiąc bardziej ogólnie, możliwe jest zdefiniowanie końca jako nieparzystego lub parzystego, niezależnie od tego, czy ma nieskończony stopień, w grafach, dla których wszystkie wierzchołki mają skończony stopień. Wtedy na takich grafach suma nieparzystych wierzchołków i nieparzystych końców jest albo parzysta, albo nieskończona.

Podgrafy

Zgodnie z twierdzeniem Gallai wierzchołki dowolnego wykresu można rozłożyć jako ${\ Displaystyle V = V_ {e} \ puchar V_ {o}}$ gdzie $)}$${\ Displaystyle G (V_ {}}$$ma$ wszystkie stopnie parzyste i wszystkie stopnie ${\ displaystyle | V_ {o}|}$ nawet przez lemat dotyczący uścisku dłoni. Udowodnił to Yair Caro w 1994 roku ${\ displaystyle | V_ {o} |/| V|> 1/ {\ sqrt {n}}},$ aw 2021 r. przedruk Ferbera Asafa i Michaela Krivelevicha wykazał, że ${\ Displaystyle | V_ {o} |/| V|> 1/10000}$ .

Złożoność obliczeniowa

Główny artykuł: PPA (złożoność)

W związku z metodą grafów wymiany służącą do udowodnienia istnienia struktur kombinatorycznych, interesujące jest pytanie, jak skutecznie można znaleźć te struktury. Załóżmy na przykład, że jako dane wejściowe podano cykl Hamiltona w grafie sześciennym; z twierdzenia Smitha wynika, że ​​istnieje drugi cykl. Jak szybko można znaleźć ten drugi cykl? Papadimitriou (1994) badał złożoność obliczeniową pytań takich jak ten lub bardziej ogólnie znajdowania drugiego wierzchołka nieparzystego stopnia, gdy dany jest pojedynczy nieparzysty wierzchołek w dużym niejawnie zdefiniowanym grafie . Określił klasa złożoności PPA do enkapsulacji problemów takich jak ten; blisko spokrewniona klasa zdefiniowana na grafach skierowanych, PPAD , przyciągnęła znaczną uwagę w algorytmicznej teorii gier, ponieważ obliczenie równowagi Nasha jest obliczeniowo równoważne najtrudniejszym problemom w tej klasie.

Problemy obliczeniowe, które okazały się kompletne dla klasy złożoności PPA, obejmują zadania obliczeniowe związane z lematem Spernera i sprawiedliwym podziałem zasobów zgodnie z twierdzeniem Hobby'ego-Rice'a .