Metoda elementów skończonych
| Równania różniczkowe |
|---|

|
| Zakres |
| Klasyfikacja |
| Rozwiązanie |
| Ludzie |
Metoda elementów skończonych ( MES ) jest popularną metodą numerycznego rozwiązywania równań różniczkowych pojawiających się w modelowaniu inżynierskim i matematycznym . Typowe obszary problemowe zainteresowań obejmują tradycyjne dziedziny analizy strukturalnej , wymiany ciepła , przepływu płynów , transportu masy i potencjału elektromagnetycznego .
MES to ogólna metoda numeryczna służąca do rozwiązywania równań różniczkowych cząstkowych w dwóch lub trzech zmiennych przestrzennych (tj. niektórych problemów brzegowych ). Aby rozwiązać problem, MES dzieli duży system na mniejsze, prostsze części, które nazywane są elementami skończonymi . Osiąga się to poprzez określoną dyskretyzację przestrzeni w wymiarach przestrzennych, która jest realizowana przez konstrukcję siatki obiektu : dziedziny numerycznej dla rozwiązania, która ma skończoną liczbę punktów. Sformułowanie problemu wartości brzegowych metodą elementów skończonych daje ostatecznie układ równań algebraicznych . Metoda przybliża nieznaną funkcję w dziedzinie. Proste równania, które modelują te elementy skończone, są następnie łączone w większy układ równań, który modeluje cały problem. MES następnie przybliża rozwiązanie poprzez minimalizację powiązanej funkcji błędu za pomocą rachunku wariacyjnego .
Badanie lub analizowanie zjawiska za pomocą MES jest często określane jako analiza elementów skończonych ( MES ).
Podstawowe koncepcje
Podział całej domeny na prostsze części ma kilka zalet:
- Dokładne odwzorowanie złożonej geometrii
- Uwzględnienie odmiennych właściwości materiałów
- Łatwe przedstawienie całego rozwiązania
- Uchwycenie efektów lokalnych.
Typowe opracowanie metody obejmuje:
- podzielenie dziedziny problemu na zbiór subdomen, przy czym każda subdomena jest reprezentowana przez zestaw równań elementów do pierwotnego problemu
- systematyczne ponowne łączenie wszystkich zestawów równań elementów w globalny układ równań do ostatecznych obliczeń.
Globalny układ równań ma znane techniki rozwiązywania i można go obliczyć na podstawie początkowych wartości pierwotnego problemu, aby uzyskać odpowiedź numeryczną.
W pierwszym kroku powyżej równania elementów są prostymi równaniami, które lokalnie przybliżają oryginalne równania zespolone, które mają być badane, przy czym oryginalne równania są często równaniami różniczkowymi cząstkowymi (PDE). Aby wyjaśnić aproksymację w tym procesie, powszechnie wprowadza się metodę elementów skończonych jako szczególny przypadek metody Galerkina . Proces, w języku matematycznym, polega na skonstruowaniu całki iloczynu wewnętrznego funkcji resztkowej i wagowej oraz ustawieniu całki na zero. Mówiąc prościej, jest to procedura, która minimalizuje błąd aproksymacji poprzez dopasowanie funkcji próbnych do PDE. Reszta to błąd spowodowany przez funkcje próbne, a funkcje wagowe to wielomianowe funkcje aproksymacyjne, które rzutują resztę. Proces eliminuje wszystkie pochodne przestrzenne z PDE, przybliżając w ten sposób lokalnie PDE
- zestaw równań algebraicznych dla problemów stanu ustalonego ,
- zestaw równań różniczkowych zwyczajnych dla problemów przejściowych .
Te zestawy równań są równaniami elementów. Są liniowe , jeśli podstawowy PDE jest liniowy i odwrotnie. Układy równań algebraicznych, które pojawiają się w problemach stanu ustalonego , są rozwiązywane przy użyciu metod numerycznej algebry liniowej , podczas gdy układy równań różniczkowych zwyczajnych , które pojawiają się w problemach przejściowych, są rozwiązywane przez całkowanie numeryczne przy użyciu standardowych technik, takich jak metoda Eulera lub metoda Runge-Kutty .
W powyższym kroku (2) globalny układ równań jest generowany z równań elementu poprzez transformację współrzędnych z węzłów lokalnych subdomen do węzłów globalnych domeny. Ta transformacja przestrzenna obejmuje odpowiednie dostosowania orientacji zastosowane w odniesieniu do układu współrzędnych odniesienia . Proces ten jest często przeprowadzany przez oprogramowanie FEM przy użyciu współrzędnych generowanych z subdomen.
Praktyczne zastosowanie MES jest znane jako analiza elementów skończonych (MES). MES stosowany w inżynierii jest narzędziem obliczeniowym do wykonywania analiz inżynierskich . Obejmuje wykorzystanie generowania siatek do dzielenia złożonego problemu na małe elementy, a także wykorzystanie oprogramowania zakodowanego za pomocą algorytmu MES. Przy stosowaniu MES złożonym problemem jest zwykle układ fizyczny z fizyką leżącą u podstaw , taką jak równanie belki Eulera-Bernoulliego , równanie ciepła lub równania Naviera-Stokesa wyrażone w równaniach PDE lub równaniach całkowych , podczas gdy podzielone małe elementy złożone problemy reprezentują różne obszary w systemie fizycznym.
MES może być używany do analizowania problemów w skomplikowanych dziedzinach (takich jak samochody i rurociągi naftowe), gdy dziedzina się zmienia (jak podczas reakcji ciała stałego z ruchomą granicą), gdy pożądana precyzja zmienia się w całej dziedzinie lub gdy rozwiązanie brakuje gładkości. Symulacje MES zapewniają cenne zasoby, ponieważ eliminują wiele przypadków tworzenia i testowania twardych prototypów w różnych sytuacjach o wysokiej wierności. [ potrzebne źródło ] Na przykład, w symulacji zderzenia czołowego możliwe jest zwiększenie dokładności przewidywania w "ważnych" obszarach, takich jak przód samochodu i zmniejszenie go w jego tylnej części (w ten sposób zmniejszając koszt symulacji). Innym przykładem może być numeryczna prognoza pogody , gdzie ważniejsze jest posiadanie dokładnych prognoz dotyczących rozwoju wysoce nieliniowych zjawisk (takich jak tropikalne cyklony w atmosferze lub wiry w oceanie) niż stosunkowo spokojne obszary.
Jasną, szczegółową i praktyczną prezentację tego podejścia można znaleźć w książce Metoda elementów skończonych dla inżynierów .
Historia
Chociaż trudno jest podać datę wynalezienia metody elementów skończonych, metoda ta wywodzi się z potrzeby rozwiązywania złożonych problemów sprężystości i analizy strukturalnej w inżynierii lądowej i lotniczej . Jego rozwój można prześledzić do prac A. Hrennikoffa i R. Couranta na początku lat 40. XX wieku. Innym pionierem był Ioannis Argyris . W ZSRR wprowadzenie praktycznego zastosowania metody wiąże się zazwyczaj z nazwiskiem Leonarda Oganesyana. Została również niezależnie odkryta ponownie w Chinach przez Feng Kanga w późnych latach pięćdziesiątych i wczesnych sześćdziesiątych XX wieku, w oparciu o obliczenia konstrukcji zapór, gdzie nazwano ją metodą różnic skończonych opartą na zasadzie wariacji . Chociaż podejścia stosowane przez tych pionierów są różne, mają jedną podstawową cechę: dyskretyzację siatki domeny ciągłej na zestaw dyskretnych subdomen, zwykle nazywanych elementami.
Praca Hrennikoffa dyskretyzuje domenę za pomocą analogii sieciowej , podczas gdy podejście Couranta dzieli domenę na skończone trójkątne podobszary, aby rozwiązać eliptyczne równania różniczkowe cząstkowe drugiego rzędu , które wynikają z problemu skręcania cylindra . Wkład Couranta był ewolucyjny, opierając się na dużej liczbie wcześniejszych wyników dla PDE opracowanych przez Rayleigha , Ritza i Galerkina .
Metoda elementów skończonych uzyskała swój prawdziwy rozpęd w latach 60 . _ _ _ i inni na Swansea University , Philippe G. Ciarlet na University of Paris 6 i Richard Gallagher ze współpracownikami na Cornell University . Dalszego rozmachu nadały w tych latach dostępne programy elementów skończonych typu open source. NASA sponsorowała oryginalną wersję NASTRAN , a UC Berkeley szeroko udostępnił program elementów skończonych SAP IV. W Norwegii towarzystwo klasyfikacyjne statków Det Norske Veritas (obecnie DNV GL ) opracowało Sesam w 1969 roku do użytku w analizie statków. Rygorystyczne matematyczne podstawy metody elementów skończonych zostały dostarczone w 1973 roku wraz z publikacją Stranga i Fixa . Od tego czasu metoda została uogólniona do modelowania numerycznego układów fizycznych w wielu różnych dyscyplinach inżynierskich , np. elektromagnetyzmie , wymianie ciepła i dynamice płynów .
Dyskusja techniczna
Struktura metod elementów skończonych
Metoda elementów skończonych charakteryzuje się sformułowaniem wariacyjnym , strategią dyskretyzacji, jednym lub większą liczbą algorytmów rozwiązania oraz procedurami przetwarzania końcowego.
Przykładami formuły wariacyjnej są metoda Galerkina , nieciągła metoda Galerkina, metody mieszane itp.
Pod pojęciem strategii dyskretyzacji rozumie się jasno określony zestaw procedur obejmujących (a) tworzenie siatek elementów skończonych, (b) definiowanie funkcji bazowych na elementach odniesienia (zwanych także funkcjami kształtu) oraz (c) mapowanie odniesienia elementy na elementy siatki. Przykładami strategii dyskretyzacji są wersja h, wersja p , wersja hp , x-MES , analiza izogeometryczna itp. Każda strategia dyskretyzacji ma pewne zalety i wady. Rozsądnym kryterium wyboru strategii dyskretyzacji jest osiągnięcie niemal optymalnej wydajności dla najszerszego zestawu modeli matematycznych w określonej klasie modeli.
Różne algorytmy rozwiązań numerycznych można podzielić na dwie szerokie kategorie; solwery bezpośrednie i iteracyjne. Algorytmy te mają na celu wykorzystanie rzadkości macierzy, które zależą od wyborów formułowania wariacyjnego i strategii dyskretyzacji.
Procedury postprocessingu są przeznaczone do ekstrakcji interesujących nas danych z rozwiązania metodą elementów skończonych. Aby spełnić wymagania weryfikacji rozwiązania, postprocesory muszą zapewnić a posteriori w odniesieniu do ilości będących przedmiotem zainteresowania. Kiedy błędy aproksymacji są większe niż to, co jest uważane za akceptowalne, dyskretyzacja musi zostać zmieniona albo przez zautomatyzowany proces adaptacyjny, albo przez działanie analityka. Istnieje kilka bardzo wydajnych postprocesorów, które umożliwiają realizację superkonwergencji .
Przykładowe problemy P1 i P2
Poniższe dwa problemy ilustrują metodę elementów skończonych.
P1 jest problemem jednowymiarowym
gdzie , funkcją a drugą pochodną u szacunek dla .
P2 jest problemem dwuwymiarowym ( problem Dirichleta )
gdzie połączonym otwartym obszarem na , której granica . gładka rozmaitość lub wielokąt ) i u drugie pochodne w odniesieniu do x } odpowiednio.
Problem P1 można rozwiązać bezpośrednio, obliczając funkcje pierwotne . Jednak ta metoda rozwiązywania problemu z wartościami granicznymi (BVP) działa tylko wtedy, gdy istnieje jeden wymiar przestrzenny i nie uogólnia się na problemy o wyższych wymiarach lub problemy, takie jak . Z tego powodu opracujemy metodę elementów skończonych dla P1 i nakreślimy jej uogólnienie na P2.
Nasze wyjaśnienie będzie przebiegać w dwóch krokach, które odzwierciedlają dwa podstawowe kroki, które należy wykonać, aby rozwiązać problem wartości brzegowych (BVP) za pomocą MES.
- W pierwszym kroku należy przeformułować oryginalne BVP w jego słabej formie. Ten krok zwykle nie wymaga żadnych obliczeń. Transformacja odbywa się ręcznie na papierze.
- Drugim krokiem jest dyskretyzacja, w której słaba postać jest dyskretyzowana w przestrzeni o skończonych wymiarach.
Po tym drugim kroku mamy konkretne formuły dla dużego, ale skończonego wymiaru problemu liniowego, którego rozwiązanie w przybliżeniu rozwiąże pierwotny BVP. Ten problem skończonych wymiarów jest następnie realizowany na komputerze .
Słaby preparat
Pierwszym krokiem jest przekształcenie P1 i P2 w ich równoważne słabe preparaty .
Słaba forma P1
Jeśli , to dla dowolnej funkcji gładkiej , która spełnia warunki brzegowe przemieszczenia, tj. w i mamy
|
|
|
() |
I odwrotnie, jeśli spełnia (1) dla każdej gładkiej funkcji \ to można pokazać, że to . Dowód jest łatwiejszy dla dwukrotnie różniczkowalnej ( twierdzenie o wartości średniej ), ale można go również udowodnić w sensie dystrybucji .
Definiujemy nowego operatora lub mapę , używając całkowania przez części po prawej stronie (1):
-
()
gdzie przyjęliśmy założenie, że .
Słaba forma P2
Jeśli całkujemy przez części, używając postaci tożsamości Greena , widzimy, że jeśli , to możemy zdefiniować dla dowolnego wg
gdzie gradient i oznacza skalarny w dwuwymiarowej Jeszcze raz można przekształcić w iloczyn wewnętrzny na odpowiedniej przestrzeni { , które są zerowe na . Założyliśmy przestrzenie _ _ Można również wykazać istnienie i niepowtarzalność rozwiązania.
Dowodowy zarys istnienia i niepowtarzalności rozwiązania
Możemy luźno myśleć o , które są H w i (patrz spacje Sobolewa ). Takie funkcje są (słabo) raz różniczkowalne i okazuje się, że symetryczna definiuje następnie iloczyn wewnętrzny , który zamienia się w w przestrzeń Hilberta (szczegółowy dowód jest nietrywialny). Z drugiej strony lewa strona jest również wewnętrzną produkt, tym razem w przestrzeni Lp . Zastosowanie twierdzenia Riesza o reprezentacji dla przestrzeni Hilberta pokazuje że istnieje unikalne (2), a zatem P1. To rozwiązanie jest a tylko członkiem ale eliptycznej gładkie .
Dyskretyzacja
P1 i P2 są gotowe do dyskretyzacji, co prowadzi do wspólnego podproblemu (3). Podstawową ideą jest zastąpienie nieskończenie wymiarowego problemu liniowego:
- Znajdź takie, że
z wersją o skończonych wymiarach:
-
Znajdź takie, że()
gdzie jest wymiarową podprzestrzenią H } Istnieje wiele możliwych wyborów możliwości prowadzi do metody spektralnej ). Jednak w przypadku metody elementów skończonych przyjmujemy, to przestrzeń fragmentarycznych funkcji wielomianowych.
Do problemu P1
Bierzemy interwał , wybieramy x z i definiujemy przez:
definiujemy i } Zauważ, że funkcje w różniczkowalne zgodnie z elementarną definicją rachunku różniczkowego. , jeśli wtedy zdefiniowana w żadnym miejscu , . Jednak pochodna istnieje przy każdej innej wartości użyć tej pochodnej do całkowania przez części .
Do problemu P2
Potrzebujemy być zbiorem funkcji . Na rysunku po prawej zilustrowaliśmy triangulację 15-bocznego obszaru wielokąta w (poniżej) oraz funkcję liniową (powyżej, w kolorze) tego wielokąta, który jest liniowy na każdy trójkąt triangulacji; przestrzeń z funkcji liniowych na każdym trójkącie wybranej triangulacji
Można mieć nadzieję, że w miarę jak leżąca pod spodem trójkątna siatka staje się coraz drobniejsza, rozwiązanie problemu dyskretnego (3) będzie w pewnym sensie zbieżne z rozwiązaniem pierwotnego problemu z wartościami brzegowymi P2. tę gęstość siatki, triangulacja jest indeksowana przez parametr o wartości rzeczywistej, który przyjmuje się za bardzo mały Ten parametr będzie związany z rozmiarem największego lub średniego trójkąta w triangulacji. Gdy udoskonalamy triangulację, przestrzeń fragmentarycznych funkcji liniowych musi się z Z tego powodu w literaturze często czyta się zamiast Ponieważ nie przeprowadzamy takiej analizy, nie będziemy używać tej notacji.
Wybór podstawy
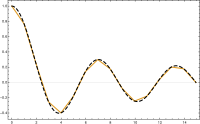
Aby zakończyć dyskretyzację musimy podstawę . W przypadku jednowymiarowym dla każdego punktu kontrolnego funkcję liniową wartość wynosi w i zero w każdym , tj.
dla ; podstawą jest przesunięta i przeskalowana funkcja namiotu . przypadku dwuwymiarowym ponownie wierzchołek obszaru . Funkcja jest unikalną funkcją , której wartość wynosi 1 {\ Displaystyle 1} w i zero .
W zależności od autora, słowo „element” w „metodzie elementów skończonych” odnosi się albo do trójkątów w dziedzinie, odcinkowo liniowej funkcji bazowej, albo do obu. Na przykład autor zainteresowany zakrzywionymi domenami może zastąpić trójkąty zakrzywionymi prymitywami, a zatem może opisać elementy jako krzywoliniowe. Z drugiej strony, niektórzy autorzy zastępują „odcinkowo liniowy” przez „odcinkowo kwadratowy” lub nawet „odcinkowo wielomian”. Autor mógłby wtedy powiedzieć „element wyższego rzędu” zamiast „wielomian wyższego stopnia”. Metoda elementów skończonych nie jest ograniczona do trójkątów (lub czworościanów w 3-d lub simpleksów wyższego rzędu w przestrzeniach wielowymiarowych), ale może być zdefiniowana na czworobocznych poddomenach (sześciany, graniastosłupy lub piramidy w 3-d itd.) . Kształty wyższego rzędu (elementy krzywoliniowe) można definiować za pomocą kształtów wielomianowych, a nawet nie wielomianowych (np. elipsa lub okrąg).
Przykładami metod wykorzystujących wielomianowe funkcje bazowe wyższego stopnia są hp-FEM i spektralny MES .
Bardziej zaawansowane implementacje (adaptacyjne metody elementów skończonych) wykorzystują metodę oceny jakości wyników (opartą na teorii szacowania błędów) i modyfikują siatkę podczas rozwiązywania, dążąc do uzyskania przybliżonego rozwiązania w pewnych granicach od dokładnego rozwiązania problemu continuum . Adaptacyjność siatki może wykorzystywać różne techniki, z których najpopularniejsze to:
- ruchome węzły (r-adaptacyjność)
- uszlachetniające (i nierafinowane) elementy (h-adaptacyjność)
- zmiana kolejności funkcji bazowych (p-adaptacyjność)
- kombinacje powyższych ( hp-adaptivity ).
Małe wsparcie podstawy

Podstawową zaletą tego wyboru podstawy jest to, że produkty wewnętrzne
I
będzie równa zero dla prawie wszystkich . (Macierz zawierająca w lokalizacji znana jako \ macierz W przypadku jednowymiarowym wsparciem jest przedział [ . Stąd całki i są identycznie zerowe, gdy .
Podobnie w przypadku planarnym, jeśli i nie mają wspólnej krawędzi triangulacji, to całki
I
oba są zerowe.
Macierzowa postać problemu
Jeśli napiszemy i następnie problem (3), biorąc dla , staje się
-
dla
()
Jeśli oznaczymy przez kolumnowe i jeśli _
I
być macierzami, których wpisy są
I
wtedy możemy przeformułować (4) jako
|
|
|
() |
Nie jest konieczne zakładanie . Dla funkcji ogólnej , problem (3) z dla staje się faktycznie prostsze, ponieważ nie jest używana żadna macierz,
|
|
|
() |
gdzie i dla .
Jak omówiliśmy wcześniej, większość wpisów ponieważ bazowe . Musimy więc teraz rozwiązać układ liniowy w nieznanym, wpisów macierzy , które musimy odwrócić, wynosi zero
Takie macierze są znane jako rzadkie macierze i istnieją skuteczne rozwiązania takich problemów (znacznie bardziej wydajne niż faktyczne macierzy). Ponadto jest i dodatnio określony, więc technika taka jak gradient sprzężony metoda jest preferowana. W przypadku problemów, które nie są zbyt duże, rzadkie dekompozycje LU i dekompozycje Cholesky'ego nadal dobrze działają. Na przykład MATLAB-a (który używa rzadkiego LU, rzadkiego Cholesky'ego i innych metod faktoryzacji) może być wystarczający dla siatek ze stu tysiącami wierzchołków.
Macierz nazywana macierzą sztywności , podczas gdy macierz macierzą mas .
Ogólna postać metody elementów skończonych
Ogólnie rzecz biorąc, metoda elementów skończonych charakteryzuje się następującym procesem.
- Wybiera się siatkę dla . W poprzednim zabiegu siatka składała się z trójkątów, ale można też użyć kwadratów lub krzywoliniowych wielokątów.
- Następnie wybiera się funkcje bazowe. W naszej dyskusji używaliśmy odcinkowo liniowych funkcji bazowych, ale często stosuje się również odcinkowo wielomianowe funkcje bazowe.
Osobną kwestią jest gładkość funkcji bazowych. W przypadku eliptycznych problemów brzegowych drugiego rzędu wystarczająca jest funkcja bazowa wielomianu częściowego, która jest jedynie ciągła (tj. pochodne są nieciągłe). W przypadku równań różniczkowych cząstkowych wyższego rzędu należy użyć gładszych funkcji bazowych. czwartego rzędu, takiego jak , .
rozważenia jest stosunek przestrzeni o skończonych wymiarach wymiarowego odpowiednika w powyższych przykładach Metoda elementu zgodnego to taka, w której przestrzeń przestrzeni elementu dla problemu ciągłego. Powyższy przykład jest taką metodą. Jeśli ten warunek nie jest spełniony, otrzymujemy metodę elementów niezgodnych, której przykładem jest przestrzeń odcinkowo liniowych funkcji nad siatką, które są ciągłe w każdym punkcie środkowym krawędzi. wzdłuż krawędzi, ta przestrzeń o skończonych wymiarach nie jest podprzestrzenią pierwotnej .
Zazwyczaj jeden ma algorytm pobierania danej siatki i jej podziału. Jeśli główną metodą zwiększania precyzji jest podział siatki, istnieje metoda h ( h jest zwykle średnicą największego elementu w siatce). W ten sposób, jeśli wykaże się, że błąd z siatką ograniczony powyżej przez i wtedy ma się porządek do metoda. wypukła), metoda fragmentarycznego wielomianu rzędu błąd .
Jeśli zamiast zmniejszać h , zwiększa się stopień wielomianów używanych w funkcji bazowej, mamy metodę p . Jeśli połączymy te dwa rodzaje udoskonalania, otrzymamy hp ( hp-FEM ). W hp-FEM stopnie wielomianu mogą różnić się w zależności od elementu. Metody wysokiego rzędu z dużym jednorodnym p nazywane są metodami spektralnymi elementów skończonych ( SFEM ). Nie należy ich mylić z metodami spektralnymi .
W przypadku wektorowych równań różniczkowych cząstkowych funkcje bazowe mogą przyjmować wartości w .
Różne typy metod elementów skończonych
AEM
Metoda Elementów Stosowanych lub AEM łączy w sobie cechy zarówno metody MES, jak i metody elementów dyskretnych lub (DEM).
A-FEM
Metoda rozszerzonych elementów skończonych została wprowadzona przez Yang i Lui, których celem było modelowanie słabych i silnych nieciągłości bez potrzeby stosowania dodatkowych DoF, jak podano w PuM.
Uogólniona metoda elementów skończonych
Uogólniona metoda elementów skończonych (GFEM) wykorzystuje lokalne przestrzenie składające się z funkcji, niekoniecznie wielomianów, które odzwierciedlają dostępne informacje o nieznanym rozwiązaniu, a tym samym zapewniają dobre lokalne przybliżenie. Następnie podział jedności , aby „związać” te przestrzenie razem, tworząc przybliżoną podprzestrzeń. Skuteczność GFEM została wykazana w przypadku zastosowania do problemów z domenami o skomplikowanych granicach, problemów z mikroskalami i problemów z warstwami granicznymi.
Mieszana metoda elementów skończonych
Mieszana metoda elementów skończonych jest rodzajem metody elementów skończonych, w której dodatkowe zmienne niezależne są wprowadzane jako zmienne węzłowe podczas dyskretyzacji problemu z równaniem różniczkowym cząstkowym.
Zmienna – wielomian
HP -FEM łączy w sposób adaptacyjny elementy o zmiennym rozmiarze h i stopniu wielomianu p , aby osiągnąć wyjątkowo szybkie, wykładnicze tempo zbieżności.
hpk-MES
HPk-MES łączy adaptacyjnie elementy o zmiennym rozmiarze h , stopniu wielomianu lokalnych przybliżeń p i globalnej różniczkowalności lokalnych przybliżeń (k-1) , aby osiągnąć najlepsze współczynniki zbieżności.
XFEM
Rozszerzona metoda elementów skończonych (XFEM) jest techniką numeryczną opartą na uogólnionej metodzie elementów skończonych (GFEM) i metodzie podziału jedności (PUM). Rozszerza klasyczną metodę elementów skończonych o wzbogacenie przestrzeni rozwiązań o rozwiązania równań różniczkowych z funkcjami nieciągłymi. Rozszerzone metody elementów skończonych wzbogacają przestrzeń aproksymacji tak, że może ona w naturalny sposób odtworzyć trudną cechę związaną z interesującym nas problemem: nieciągłość, osobliwość, warstwę graniczną itp. Wykazano, że dla niektórych problemów takie osadzenie cechy problemu w przestrzeń aproksymacji może znacznie poprawić współczynniki zbieżności i dokładność. Co więcej, rozwiązywanie problemów z nieciągłościami za pomocą XFEM eliminuje potrzebę tworzenia siatki i ponownego tworzenia siatki powierzchni nieciągłości, zmniejszając w ten sposób koszty obliczeniowe i błędy projekcji związane z konwencjonalnymi metodami elementów skończonych, kosztem ograniczenia nieciągłości do krawędzi siatki.
Kilka kodów badawczych implementuje tę technikę w różnym stopniu: 1. GetFEM++ 2. xfem++ 3. openxfem++
XFEM został również zaimplementowany w kodach takich jak Altair Radios, ASTER, Morfeo i Abaqus. Jest coraz częściej przyjmowany przez inne komercyjne oprogramowanie elementów skończonych, z kilkoma dostępnymi wtyczkami i faktycznymi implementacjami rdzenia (ANSYS, SAMCEF, OOFELIE itp.).
Metoda skalowanych brzegowych elementów skończonych (SBFEM)
Wprowadzenie metody skalowanych brzegowych elementów skończonych (SBFEM) pochodzi od Song and Wolf (1997). SBFEM był jednym z najbardziej dochodowych wkładów w dziedzinie analizy numerycznej problemów mechaniki pękania. Jest to półanalityczna metoda fundamentalno-bezrozwiązania, która łączy w sobie zalety formuł i procedur elementów skończonych oraz dyskretyzacji elementów brzegowych. Jednak w przeciwieństwie do metody elementów brzegowych nie jest wymagane żadne fundamentalne rozwiązanie różniczkowe.
S-FEM
S-FEM, Smoothed Finite Element Methods, to szczególna klasa algorytmów symulacji numerycznej do symulacji zjawisk fizycznych. Został opracowany przez połączenie metod bezsiatkowych z metodą elementów skończonych.
Metoda elementów widmowych
Metody elementów widmowych łączą w sobie elastyczność geometryczną elementów skończonych i wysoką dokładność metod widmowych. Metody spektralne to przybliżone rozwiązania równań cząstkowych postaci słabej, które są oparte na interpolantach Lagrange'a wysokiego rzędu i są używane tylko z pewnymi regułami kwadraturowymi.
Metody bez siatki
Nieciągłe metody Galerkina
Analiza granic elementów skończonych
Metoda rozciągniętej siatki
iteracja Loubignaca
Iteracja Loubignaca jest metodą iteracyjną w metodach elementów skończonych.
Metoda elementów skończonych plastyczności kryształów (CPFEM)
Metoda elementów skończonych plastyczności kryształów (CPFEM) to zaawansowane narzędzie numeryczne opracowane przez Franza Rotersa. Metale można uznać za agregaty krystaliczne i zachowują się anizotropowo pod wpływem odkształcenia, na przykład nieprawidłowej lokalizacji naprężeń i odkształceń. CPFEM w oparciu o poślizg (szybkość odkształcenia ścinającego) może obliczyć dyslokację, orientację kryształów i inne informacje o teksturze, aby uwzględnić anizotropię kryształu podczas rutyny. Obecnie stosuje się ją w badaniach numerycznych deformacji materiałów, chropowatości powierzchni, pęknięć itp.
Metoda elementu wirtualnego (VEM)
Metoda elementu wirtualnego (VEM), wprowadzona przez Beirão da Veiga i in. (2013) jako rozszerzenie mimetycznych różnic skończonych (MFD), jest uogólnieniem standardowej metody elementów skończonych dla dowolnych geometrii elementów. Pozwala to na dopuszczenie ogólnych wielokątów (lub wielościanów w 3D), które są bardzo nieregularne i nie mają kształtu wypukłego. Nazwa virtual wywodzi się z faktu, że znajomość lokalnej podstawy funkcji kształtu nie jest wymagana i w rzeczywistości nigdy nie jest jawnie obliczana.
Powiązanie z metodą dyskretyzacji gradientowej
Niektóre typy metod elementów skończonych (zgodne, niezgodne, mieszane metody elementów skończonych) są szczególnymi przypadkami metody dyskretyzacji gradientowej (GDM). Stąd właściwości konwergencji GDM, które są ustalone dla szeregu problemów (liniowe i nieliniowe problemy eliptyczne, liniowe, nieliniowe i zdegenerowane problemy paraboliczne), zachowują się również dla tych konkretnych MES.
Porównanie z metodą różnic skończonych
Metoda różnic skończonych (FDM) jest alternatywnym sposobem aproksymacji rozwiązań PDE. Różnice między FEM i FDM to:
- Najbardziej atrakcyjną cechą FEM jest jego zdolność do stosunkowo łatwego radzenia sobie ze skomplikowanymi geometriami (i granicami). Podczas gdy FDM w swojej podstawowej formie ogranicza się do obsługi kształtów prostokątnych i ich prostych zmian, obsługa geometrii w MES jest teoretycznie prosta.
- FDM nie jest zwykle używany do nieregularnych geometrii CAD, ale częściej do modeli prostokątnych lub blokowych.
- FEM generalnie pozwala na bardziej elastyczną adaptację siatki niż FDM.
- Najbardziej atrakcyjną cechą różnic skończonych jest to, że jest bardzo łatwa do wdrożenia.
- Istnieje kilka sposobów, w jakie można uznać FDM za szczególny przypadek podejścia MES. Np. MES pierwszego rzędu jest identyczny z FDM dla równania Poissona , jeśli problem jest dyskretyzowany przez regularną prostokątną siatkę z każdym prostokątem podzielonym na dwa trójkąty.
- Istnieją powody, aby uznać matematyczne podstawy aproksymacji elementów skończonych za bardziej solidne, na przykład dlatego, że jakość aproksymacji między punktami siatki jest słaba w FDM.
- Jakość przybliżenia MES jest często wyższa niż w odpowiednim podejściu FDM, ale jest to bardzo zależne od problemu i można podać kilka przykładów przeciwnych.
Ogólnie rzecz biorąc, MES jest metodą z wyboru we wszystkich typach analiz w mechanice strukturalnej (tj. rozwiązywaniu odkształceń i naprężeń w ciałach stałych lub dynamice konstrukcji), podczas gdy obliczeniowa dynamika płynów (CFD) zwykle wykorzystuje FDM lub inne metody, takie jak metoda skończonych objętości ( FVM). Problemy CFD zwykle wymagają dyskretyzacji problemu na dużą liczbę komórek / punktów siatki (miliony i więcej), dlatego koszt rozwiązania sprzyja prostszemu przybliżeniu niższego rzędu w każdej komórce. Jest to szczególnie prawdziwe w przypadku problemów z „przepływem zewnętrznym”, takich jak przepływ powietrza wokół samochodu lub samolotu lub symulacja pogody.
Aplikacja
Różnorodne specjalizacje w ramach dyscypliny inżynierii mechanicznej (takie jak przemysł lotniczy, biomechaniczny i motoryzacyjny) powszechnie wykorzystują zintegrowane MES w projektowaniu i rozwoju swoich produktów. Kilka nowoczesnych pakietów MES zawiera określone komponenty, takie jak termiczne, elektromagnetyczne, płynne i strukturalne środowiska pracy. W symulacji strukturalnej FEM ogromnie pomaga w tworzeniu wizualizacji sztywności i wytrzymałości, a także w minimalizowaniu masy, materiałów i kosztów.
MES umożliwia szczegółową wizualizację miejsc zginania lub skręcania konstrukcji oraz wskazuje rozkład naprężeń i przemieszczeń. Oprogramowanie FEM zapewnia szeroki zakres opcji symulacji do kontrolowania złożoności zarówno modelowania, jak i analizy systemu. Podobnie, wymagany poziom wymaganej dokładności i związane z nim wymagania dotyczące czasu obliczeniowego mogą być zarządzane jednocześnie w celu obsługi większości aplikacji inżynierskich. MES umożliwia konstruowanie, udoskonalanie i optymalizację całych projektów przed ich wyprodukowaniem. Siatka jest integralną częścią modelu i musi być dokładnie kontrolowana, aby uzyskać najlepsze rezultaty. Ogólnie rzecz biorąc, im większa liczba elementów w siatce, tym dokładniejsze rozwiązanie dyskretyzowanego problemu. Istnieje jednak wartość, przy której wyniki są zbieżne, a dalsze udoskonalanie siatki nie zwiększa dokładności.
To potężne narzędzie do projektowania znacznie poprawiło zarówno standard projektów inżynierskich, jak i metodologię procesu projektowania w wielu zastosowaniach przemysłowych. Wprowadzenie FEM znacznie skróciło czas potrzebny do przeniesienia produktów od koncepcji do linii produkcyjnej. Testowanie i rozwój zostały przyspieszone przede wszystkim dzięki udoskonalonym projektom wstępnych prototypów z wykorzystaniem MES. Podsumowując, zalety MES obejmują zwiększoną dokładność, ulepszony projekt i lepszy wgląd w krytyczne parametry projektowe, wirtualne prototypowanie, mniej prototypów sprzętowych, szybszy i tańszy cykl projektowania, zwiększoną produktywność i zwiększone przychody.
W latach 90. zaproponowano MES do wykorzystania w modelowaniu stochastycznym do numerycznego rozwiązywania modeli prawdopodobieństwa, a później do oceny niezawodności.
Zobacz też
- Zastosowana metoda elementów
- Metoda elementów brzegowych
- Lemat Céa
- Eksperyment komputerowy
- Bezpośrednia metoda sztywności
- Optymalizacja układu nieciągłości
- Metoda elementów dyskretnych
- Metoda różnic skończonych
- Maszyna elementów skończonych
- Metoda elementów skończonych w mechanice budowli
- Metoda objętości skończonej
- Metoda objętości skończonych dla przepływu nieustalonego
- Metoda elementów nieskończonych
- Przedziałowy element skończony
- Analiza izogeometryczna
- Kratowe metody Boltzmanna
- Lista pakietów oprogramowania elementów skończonych
- Metody bez siatki
- Ruchomy automat komórkowy
- Multidyscyplinarna optymalizacja projektu
- Multifizyka
- Test płatkowy
- Metoda Rayleigha-Ritza
- Mapowanie przestrzeni
- CIĄG 7
- Teselacja (grafika komputerowa)
- Osłabiona słaba forma
Dalsza lektura
- G. Allaire i A. Craig: Analiza numeryczna i optymalizacja: wprowadzenie do modelowania matematycznego i symulacji numerycznej .
- KJ Bathe: Metody numeryczne w analizie elementów skończonych , Prentice-Hall (1976).
- Thomas JR Hughes: Metoda elementów skończonych: liniowa statyczna i dynamiczna analiza elementów skończonych, Prentice-Hall (1987).
- J. Chaskalovic: Metody elementów skończonych dla nauk inżynierskich , Springer Verlag, (2008).
- Endre Süli : metody elementów skończonych dla równań różniczkowych cząstkowych .
- OC Zienkiewicz, RL Taylor, JZ Zhu: Metoda elementów skończonych: podstawy i podstawy , Butterworth-Heinemann (2005).
- N. Ottosen, H. Petersson: Wprowadzenie do metody elementów skończonych, Prentice-Hall (1992).
- Zohdi, TI (2018) Elementarz skończony dla początkujących - wersja rozszerzona zawierająca przykładowe testy i projekty. Wydanie drugie https://link.springer.com/book/10.1007/978-3-319-70428-9
















































![{\displaystyle V=\{v:[0,1]\rightarrow \mathbb {R} \;:v{\mbox{ is continuous, }}v|_{[x_{k},x_{k+1}]}{\mbox{ is linear for }}k=0,\dots ,n{\mbox{, and }}v(0)=v(1)=0\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d72f354ee5b50866296ad9e758f442f6a32d4b32)









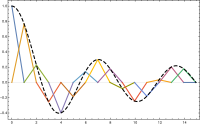




![{\displaystyle v_{k}(x)={\begin{cases}{x-x_{k-1} \over x_{k}\,-x_{k-1}}&{\mbox{ if }}x\in [x_{k-1},x_{k}],\\{x_{k+1}\,-x \over x_{k+1}\,-x_{k}}&{\mbox{ if }}x\in [x_{k},x_{k+1}],\\0&{\mbox{ otherwise}},\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d8df33dbf412ea446944402c80c7cab51ecd7e)










![[x_{k-1},x_{k+1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9ab905e7068db95aeddfd9f0fa55af0e0363843)




































