Analiza strukturalna

Ten artykuł jest o badaniach strukturalnych w inżynierii. Aby zapoznać się z zastosowaniami nauk społecznych, zobacz Strukturalizm . W przypadku innych zastosowań zobacz Struktura (ujednoznacznienie) .

Analiza strukturalna jest gałęzią mechaniki brył , która wykorzystuje uproszczone modele brył, takich jak pręty, belki i skorupy, do podejmowania decyzji inżynierskich. Jego głównym celem jest określenie wpływu obciążeń na konstrukcje fizyczne i ich elementy . W przeciwieństwie do teorii sprężystości modele stosowane w analizie konstrukcji to często równania różniczkowe w jednej zmiennej przestrzennej. Konstrukcje podlegające tego typu analizie obejmują wszystko, co musi wytrzymać obciążenia, takie jak budynki, mosty, samoloty i statki. Analiza strukturalna wykorzystuje idee mechaniki stosowanej , materiałoznawstwa i matematyki stosowanej do obliczania odkształceń konstrukcji , sił wewnętrznych , naprężeń , reakcji podporowych, prędkości, przyspieszeń i stabilności . Wyniki analizy służą weryfikacji przydatności konstrukcji do użytkowania, często z pominięciem badań fizycznych . Analiza strukturalna jest zatem kluczową częścią projektowanie inżynierskie konstrukcji .

Konstrukcje i obciążenia

W kontekście analizy strukturalnej struktura odnosi się do korpusu lub systemu połączonych części używanych do podtrzymywania obciążenia. Ważne przykłady związane z inżynierią lądową obejmują budynki, mosty i wieże; aw innych gałęziach inżynierii ważne są ramy statków i samolotów, zbiorniki, zbiorniki ciśnieniowe, systemy mechaniczne i elektryczne konstrukcje wsporcze. Aby zaprojektować konstrukcję, inżynier musi wziąć pod uwagę jej bezpieczeństwo, estetykę i użyteczność, biorąc pod uwagę ograniczenia ekonomiczne i środowiskowe. Inne gałęzie inżynierii pracują nad szeroką gamą konstrukcji innych niż budowlane .

Klasyfikacja konstrukcji

System konstrukcyjny to połączenie elementów konstrukcyjnych i ich materiałów. Ważne jest, aby inżynier budowlany był w stanie sklasyfikować konstrukcję według jej formy lub funkcji, rozpoznając różne elementy składające się na tę konstrukcję. Elementami konstrukcyjnymi przewodzącymi siły systemowe przez materiały są nie tylko korbowód, kratownica, belka czy słup, ale także kabel, łuk, wnęka lub kanał, a nawet kątownik, struktura powierzchniowa lub ramkę.

Masa

Główny artykuł: Obciążenie strukturalne

Po zdefiniowaniu wymagań wymiarowych dla konstrukcji konieczne staje się określenie obciążeń, jakie konstrukcja musi wytrzymać. Projekt konstrukcyjny zaczyna się zatem od określenia obciążeń działających na konstrukcję. Obciążenie projektowe konstrukcji jest często określane w przepisach budowlanych . Istnieją dwa rodzaje przepisów: ogólne przepisy budowlane i przepisy projektowe, inżynierowie muszą spełnić wszystkie wymagania przepisów, aby konstrukcja pozostała niezawodna.

Istnieją dwa rodzaje obciążeń, które inżynieria konstrukcji musi napotkać w projekcie. Pierwszym rodzajem obciążeń są obciążenia stałe, które składają się z ciężarów różnych elementów konstrukcyjnych oraz ciężarów wszelkich obiektów trwale przymocowanych do konstrukcji. Na przykład kolumny, belki, dźwigary, płyta stropowa, pokrycia dachowe, ściany, okna, instalacja wodno-kanalizacyjna, osprzęt elektryczny i inne różne elementy mocujące. Drugi rodzaj obciążeń to obciążenia użytkowe, które różnią się wielkością i lokalizacją. Istnieje wiele różnych rodzajów obciążeń użytkowych, takich jak obciążenia budynków, obciążenia mostów autostradowych, obciążenia mostów kolejowych, obciążenia udarowe, obciążenia wiatrem, obciążenia śniegiem, obciążenia trzęsieniami ziemi i inne obciążenia naturalne.

Metody analityczne

Aby przeprowadzić dokładną analizę, inżynier budowlany musi określić takie informacje, jak obciążenia konstrukcyjne , geometria , warunki podparcia i właściwości materiałów. Wyniki takiej analizy zazwyczaj obejmują reakcje podporowe, naprężenia i przemieszczenia . Informacje te są następnie porównywane z kryteriami wskazującymi na warunki awarii. Zaawansowana analiza strukturalna może badać reakcję dynamiczną , stabilność i zachowanie nieliniowe . Istnieją trzy podejścia do analizy: tzw mechaniki materiałów (znane również jako wytrzymałość materiałów), podejście teorii sprężystości (która jest w rzeczywistości szczególnym przypadkiem bardziej ogólnej dziedziny mechaniki ośrodków ciągłych ) oraz element skończony zbliżać się. Pierwsze dwa wykorzystują sformułowania analityczne, które stosują głównie proste liniowe modele sprężyste, prowadzące do rozwiązań w postaci zamkniętej i często można je rozwiązać ręcznie. Podejście elementów skończonych jest w rzeczywistości metodą numeryczną rozwiązywania równań różniczkowych generowanych przez teorie mechaniki, takie jak teoria sprężystości i wytrzymałość materiałów. Jednak metoda elementów skończonych zależy w dużej mierze od mocy obliczeniowej komputerów i ma większe zastosowanie do struktur o dowolnej wielkości i złożoności.

Niezależnie od podejścia, sformułowanie opiera się na tych samych trzech podstawowych relacjach: równowagi , konstytutywnej i kompatybilności . Rozwiązania są przybliżone, gdy którakolwiek z tych relacji jest spełniona tylko w przybliżeniu lub tylko w przybliżeniu rzeczywistości.

Ograniczenia

Każda metoda ma godne uwagi ograniczenia. Metoda mechaniki materiałów ogranicza się do bardzo prostych elementów konstrukcyjnych w stosunkowo prostych warunkach obciążenia. Dozwolone elementy konstrukcyjne i warunki obciążenia są jednak wystarczające do rozwiązania wielu użytecznych problemów inżynierskich. Teoria sprężystości zasadniczo pozwala na rozwiązywanie elementów konstrukcyjnych o ogólnej geometrii w ogólnych warunkach obciążenia. Rozwiązanie analityczne ogranicza się jednak do stosunkowo prostych przypadków. Rozwiązanie zagadnień sprężystości wymaga również rozwiązania układu równań różniczkowych cząstkowych, co jest znacznie bardziej wymagające matematycznie niż rozwiązanie zagadnień mechaniki materiałów, które wymagają co najwyżej rozwiązania równania różniczkowego zwyczajnego. Metoda elementów skończonych jest chyba najbardziej restrykcyjna i jednocześnie najbardziej użyteczna. Ta metoda sama w sobie opiera się na innych teoriach strukturalnych (takich jak pozostałe dwie omówione tutaj) w celu rozwiązania równań. Jednak ogólnie umożliwia rozwiązywanie tych równań, nawet przy bardzo złożonej geometrii i warunkach obciążenia, z zastrzeżeniem, że zawsze występuje jakiś błąd numeryczny. Skuteczne i niezawodne stosowanie tej metody wymaga solidnego zrozumienia jej ograniczeń.

Metody wytrzymałości materiałów (metody klasyczne)

Najprostsza z trzech omówionych tutaj metod, metoda mechaniki materiałów, jest dostępna dla prostych elementów konstrukcyjnych poddanych określonym obciążeniom, takich jak pręty obciążone osiowo, belki graniastosłupowe w stanie czystego zginania oraz okrągłe wały poddane skręcaniu. Rozwiązania można w pewnych warunkach nałożyć, stosując zasadę superpozycji , aby przeanalizować pręt poddawany obciążeniom kombinowanym. Istnieją rozwiązania dla specjalnych przypadków dla typowych konstrukcji, takich jak cienkościenne zbiorniki ciśnieniowe.

Do analizy całych systemów podejście to można zastosować w połączeniu ze statyką, dając początek metodzie przekrojów i metodzie połączeń do analizy kratownic , metodzie rozkładu momentów dla małych ram sztywnych oraz metodzie ram portalowych i wspornikowych dla dużych ram sztywnych . Poza rozkładem momentów, który wszedł do użytku w latach trzydziestych XX wieku, metody te rozwinęły się w obecnej postaci w drugiej połowie XIX wieku. Są nadal używane do małych konstrukcji i do wstępnego projektowania dużych konstrukcji.

Rozwiązania oparte są na liniowej izotropowej nieskończenie małej sprężystości i teorii wiązki Eulera-Bernoulliego. Innymi słowy, zawierają założenia (między innymi), że badane materiały są sprężyste, że naprężenie jest związane liniowo z odkształceniem, że materiał (ale nie konstrukcja) zachowuje się identycznie niezależnie od kierunku przyłożonego obciążenia, że ​​wszystkie odkształcenia są małe, a belki są długie w stosunku do ich głębokości. Jak w przypadku każdego upraszczającego założenia w inżynierii, im bardziej model odbiega od rzeczywistości, tym mniej użyteczny (i bardziej niebezpieczny) jest wynik.

Przykład

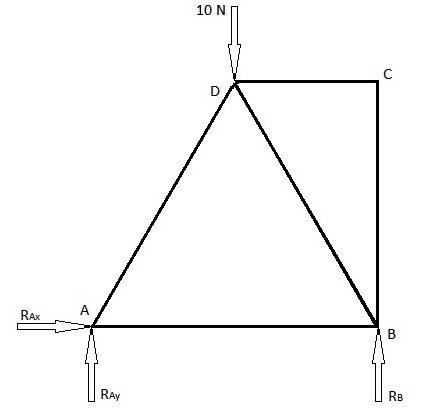
Istnieją 2 powszechnie stosowane metody znajdowania sił elementu kratownicy, a mianowicie metoda połączeń i metoda przekrojów. Poniżej znajduje się przykład, który został rozwiązany przy użyciu obu tych metod. Pierwszy diagram poniżej to przedstawiony problem, dla którego należy znaleźć siły elementu kratownicy. Drugi wykres jest wykresem obciążenia i zawiera siły reakcji z połączeń.

Ponieważ w punkcie A znajduje się połączenie sworzniowe, będzie ono miało 2 siły reakcji. Jeden w kierunku x, a drugi w kierunku y. W punkcie B znajduje się przegub rolkowy, a więc tylko 1 siła reakcji w kierunku y. Zakładając, że siły te są skierowane w odpowiednich kierunkach dodatnich (jeśli nie są w kierunkach dodatnich, wartość będzie ujemna).

Ponieważ układ znajduje się w równowadze statycznej, suma sił działających w dowolnym kierunku wynosi zero, a suma momentów względem dowolnego punktu jest równa zeru. Dlatego można obliczyć wielkość i kierunek sił reakcji.

${\ Displaystyle \ suma M_ {A} = 0 = -10 * 1 + 2 * R_ {B} \ Strzałka w prawo R_ {B} =$

${\ Displaystyle \ suma F_ {y} = 0 = R_ {Ay} + R_ {B} -10 \ Strzałka w prawo R_ {Ay} = 5}$

${\ Displaystyle \ suma F_ {x} = 0 = R_ {Ax}}$

Metoda stawów

Ten typ metody wykorzystuje równowagę sił w kierunkach x i y na każdym ze złączy w konstrukcji kratownicy.

w A,

${y} = 0 = R_ {Ay} + F_{AD}\sin(60)=5+F_{AD}{\frac {\sqrt {3}}{2}}\strzałka w prawo F_{AD}=-{\frac {10}{\sqrt {3} }}}$

${\ Displaystyle \ suma F_ {x} = 0 = R_ {Ax} + F_ {AD} \ cos(60)+F_{AB}=0-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_{AB}\strzałka w prawo F_{AB}={\ frac {5}{\sqrt {3}}}}$

w D,

${\ Displaystyle \ suma F_ {y} = 0 = -10-F_ {AD} \ sin (60) -F_ {BD} \ sin (60) = -10- \ lewo (- {\ Frac {10} {\ sqrt {3}}}\right){\frac {\sqrt {3}}{2}}-F_{BD}{\frac {\sqrt {3}}{2}}\Strzałka w prawo F_{BD}=- {\ Frac {10} {\ sqrt {3}}}}$

${\ Displaystyle \ suma F_ {x} = 0 = - F_ {AD} \ cos (60) + F_ {BD} \ cos (60) + F_ {CD} = - { \frac {10}{\sqrt {3}}}{\frac {1}{2}}+{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_ {CD}\strzałka w prawo F_{CD}=0}$

w C,

${\ Displaystyle \ suma F_ {y} = 0 = - F_ {BC} \ Strzałka w prawo F_ {BC} = 0}$

Chociaż siły w każdym z elementów kratownicy zostały znalezione, dobrą praktyką jest weryfikacja wyników poprzez uzupełnienie pozostałych bilansów sił.

$\ Displaystyle \ suma F_ {x} = - F_ {CD} = - 0 = 0 \ strzałka w prawo zweryfikowana}$

w B,

${\ Displaystyle \ suma F_ {y}$

$\ Displaystyle \ suma F_ {x} = - F_ {AB} - F_{BD}\cos(60)={\frac {5}{\sqrt {3}}}-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}= 0\strzałka w prawo zweryfikowana}$

Metoda sekcji

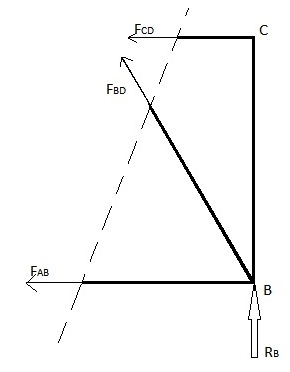
Metodę tę można zastosować, gdy trzeba znaleźć siły elementu kratownicy tylko dla kilku prętów. Metoda ta polega na wprowadzeniu pojedynczej linii prostej przecinającej pręt, którego siłę należy obliczyć. Jednak ta metoda ma ograniczenia polegające na tym, że linia cięcia może przechodzić przez maksymalnie tylko 3 elementy konstrukcji kratownicy. To ograniczenie wynika z faktu, że ta metoda wykorzystuje bilanse sił w kierunku x i y oraz bilans momentów, co daje maksymalnie 3 równania, aby znaleźć maksymalnie 3 nieznane siły elementu kratownicy, przez które wykonywane jest to cięcie. Znajdź siły FAB, FBD i FCD w powyższym przykładzie

Metoda 1: Zignoruj ​​prawą stronę

${\ Displaystyle \ suma M_ {D} = 0 = -5 * 1 + {\ sqrt {3}} * F_ {AB }\strzałka w prawo F_{AB}={\frac {5}{\sqrt {3}}}}$

${\ Displaystyle \ suma F_ {y} = 0 = R_ {Ay} -F_ {BD} \ sin (60) -10 = 5-F_ {BD} \frac {\sqrt {3}}{2}}-10\strzałka w prawo F_{BD}=-{\frac {10}{\sqrt {3}}}}$

$\ Displaystyle \ suma F_ {x} = 0 = F_ {AB} + F_ {BD} \ cos (60) + F_ {CD} = {\ Frac {5} {\ sqrt {3}}}-{\frac {10}{\sqrt {3}}}{\frac {1}{2}}+F_{CD}\Strzałka w prawo F_{CD}=0}$

Metoda 2: Zignoruj ​​lewą stronę

$\ Displaystyle \ suma M_ {B} = 0 = {\ sqrt {3}} * F_ {CD} \ strzałka w prawo F_ {CD} = 0}$

${\ Displaystyle \ suma F_ {y} = 0 = F_ {BD} \ sin (60) + R_ {B} = F_ {BD} {\ Frac {\ sqrt {3}} {2}} + 5 \ Strzałka w prawo F_ {BD} = - {\ Frac {10}{\sqrt {3}}}}$

${\ Displaystyle \ suma F_ {x} = 0 = - F_ {AB} -F_ {BD} \ cos (60) -F_ {CD} = - F_ {AB} - \ lewo (- {\ Frac {10} \sqrt {3}}}\right){\frac {1}{2}}-0\strzałka w prawo F_{AB}={\frac {5}{\sqrt {3}}}}$

Siły elementów kratownicy w pozostałych prętach można znaleźć, stosując powyższą metodę z przekrojem przechodzącym przez pozostałe pręty.

Metody sprężystości

Metody sprężystości są ogólnie dostępne dla elastycznej bryły o dowolnym kształcie. Można modelować poszczególne elementy, takie jak belki, słupy, wały, płyty i powłoki. Rozwiązania wyprowadza się z równań sprężystości liniowej . Równania sprężystości to układ 15 równań różniczkowych cząstkowych. Ze względu na charakter stosowanej matematyki rozwiązania analityczne można tworzyć tylko dla stosunkowo prostych geometrii. W przypadku złożonych geometrii konieczna jest numeryczna metoda rozwiązania, taka jak metoda elementów skończonych.

Metody wykorzystujące przybliżenie numeryczne

Powszechną praktyką jest stosowanie przybliżonych rozwiązań równań różniczkowych jako podstawy analizy strukturalnej. Zwykle odbywa się to za pomocą technik aproksymacji numerycznej. Najczęściej stosowaną aproksymacją numeryczną w analizie strukturalnej jest Metoda Elementów Skończonych .

Metoda elementów skończonych przybliża konstrukcję jako zespół elementów lub komponentów z różnymi formami połączeń między nimi, z których każdy element ma powiązaną sztywność. Tak więc system ciągły, taki jak płyta lub powłoka, jest modelowany jako system dyskretny ze skończoną liczbą elementów połączonych ze sobą w skończonej liczbie węzłów, a ogólna sztywność jest wynikiem dodania sztywności różnych elementów. Zachowanie się poszczególnych elementów charakteryzuje relacja sztywności (lub elastyczności) elementu. Połączenie różnych sztywności w główną macierz sztywności, która reprezentuje całą konstrukcję, prowadzi do relacji sztywności lub elastyczności systemu. Aby ustalić sztywność (lub elastyczność) konkretnego elementu, możemy użyć mechaniki materiałów dla prostych jednowymiarowych elementów prętowych oraz podejście sprężyste dla bardziej złożonych elementów dwu- i trójwymiarowych. Rozwój analityczny i obliczeniowy najlepiej przeprowadza się za pomocą algebry macierzowej , rozwiązując równania różniczkowe cząstkowe .

Wczesne zastosowania metod macierzowych zastosowano do konstrukcji przegubowych z elementami kratownicowymi, belkowymi i słupowymi; późniejsze i bardziej zaawansowane metody macierzowe, zwane „ analizą elementów skończonych ”, modelują całą konstrukcję za pomocą elementów jedno-, dwu- i trójwymiarowych i mogą być stosowane do układów przegubowych razem z układami ciągłymi, takimi jak zbiornik ciśnieniowy , płyty , skorupy i bryły trójwymiarowe. Komercyjne oprogramowanie komputerowe do analizy strukturalnej zwykle wykorzystuje macierzową analizę elementów skończonych, którą można dalej podzielić na dwa główne podejścia: metodę przemieszczenia lub sztywności oraz metoda siły lub elastyczności . Metoda sztywności jest zdecydowanie najbardziej popularna ze względu na łatwość wykonania, jak również recepturę dla zaawansowanych zastosowań. Technologia elementów skończonych jest obecnie wystarczająco zaawansowana, aby obsłużyć prawie każdy system, o ile dostępna jest wystarczająca moc obliczeniowa. Jego zastosowanie obejmuje między innymi analizę liniową i nieliniową, interakcje ciał stałych i płynów, materiały izotropowe, ortotropowe lub anizotropowe oraz efekty zewnętrzne, które są czynnikami statycznymi, dynamicznymi i środowiskowymi. Nie oznacza to jednak, że obliczone rozwiązanie będzie automatycznie niezawodne, ponieważ wiele zależy od modelu i wiarygodności wprowadzonych danych.

Oś czasu

• 1452-1519 Leonardo da Vinci wniósł wiele wkładu
• 1638: Galileo Galilei opublikował książkę „ Dwie nowe nauki ”, w której zbadał niepowodzenie prostych struktur
• 1660: Prawo Hooke'a autorstwa Roberta Hooke'a
• 1687: Isaac Newton opublikował „ Philosophiae Naturalis Principia Mathematica ”, która zawiera prawa dynamiki Newtona
• 1750: Równanie belki Eulera – Bernoulliego
• 1700-1782: Daniel Bernoulli wprowadził zasadę pracy wirtualnej
• 1707–1783: Leonhard Euler opracował teorię wyboczenia kolumn
• 1826: Claude-Louis Navier opublikował traktat o elastycznych zachowaniach konstrukcji
• 1873: Carlo Alberto Castigliano przedstawił swoją rozprawę „ Intorno ai sistemi elastici ”, która zawiera jego twierdzenie o obliczaniu przemieszczenia jako częściowej pochodnej energii odkształcenia. Twierdzenie to obejmuje metodę „najmniejszej pracy” jako przypadek szczególny
• 1878-1972 Stephen Timoshenko, ojciec współczesnej mechaniki stosowanej , w tym teorii wiązki Timoshenko – Ehrenfest
• 1936: Publikacja Hardy'ego Crossa dotycząca metody rozkładu momentu, która została później uznana za formę metody relaksacji mającej zastosowanie do problemu przepływu w sieci rurociągów
• 1941: Alexander Hrennikoff przedłożył doktorat. praca magisterska na MIT na temat dyskretyzacji płaskich problemów sprężystości za pomocą sieci kratowej
• 1942: R. Courant podzielił domenę na skończone podregiony
• 1956: artykuł J. Turnera, RW Clougha, HC Martina i LJ Toppa na temat „Sztywności i ugięcia złożonych struktur” wprowadza nazwę „metoda elementów skończonych” i jest powszechnie uznawany za pierwsze kompleksowe podejście do tej metody w jej obecnej postaci znane dzisiaj

Zobacz też

• Projekt stanu granicznego
• Teoria inżynierii budowlanej
• Integralność strukturalna i awaria
• Analiza naprężenia i odkształcenia
• Kryterium plastyczności von Misesa
• Probabilistyczna ocena struktur
• Testy strukturalne