hp-MES



hp-FEM to ogólna wersja metody elementów skończonych (MES), numerycznej metody rozwiązywania równań różniczkowych cząstkowych opartej na przybliżeniach częściowych wielomianów , która wykorzystuje elementy o zmiennej wielkości (h) i stopniu wielomianu (p) . Początki hp-MES sięgają pionierskich prac Barny A. Szabó i Ivo Babuški, którzy odkryli, że metoda elementów skończonych zbiega się wykładniczo szybko gdy siatka jest udokładniana za pomocą odpowiedniej kombinacji h-uszczegółnień (podział elementów na mniejsze) i p-uszczegółowień (zwiększenie stopnia ich wielomianu). Zbieżność wykładnicza sprawia, że ​​metoda ta jest bardzo atrakcyjna w porównaniu z większością innych metod elementów skończonych, które zbiegają się tylko z szybkością algebraiczną. Wykładnicza zbieżność hp-FEM została nie tylko przewidziana teoretycznie, ale także zaobserwowana przez wielu niezależnych badaczy.

Różnice w stosunku do standardowego MES

HP-FEM różni się od standardowego (najniższego rzędu) MES pod wieloma względami.

  • Wybór funkcji kształtu wyższego rzędu [ potrzebny przykład ] : Wielomiany wyższego stopnia w elementach można generować przy użyciu różnych zestawów funkcji kształtu. Wybór takiego zestawu może znacząco wpłynąć na uwarunkowanie macierzy sztywności, a co za tym idzie na cały proces rozwiązania. Problem ten został po raz pierwszy udokumentowany przez Babuską i in.
  • Automatyczna adaptacja HP : W hp-FEM element można udoskonalić HP na wiele różnych sposobów, takich jak: Zwiększenie stopnia wielomianu bez dzielenia go w przestrzeni lub geometryczny podział elementu, gdzie można zastosować różne stopnie wielomianu do podelementy. Liczba kandydatów do udoskonalenia elementów łatwo dochodzi do 100 w dwóch wymiarach i 1000 w trzech wymiarach. Jedna liczba wskazująca rozmiar błędu w elemencie nie wystarczy, aby kierować automatyczną adaptacją hp (w przeciwieństwie do adaptacyjności w standardowym MES). Inne techniki, takie jak rozwiązania referencyjne lub kwestie analityczne należy zastosować, aby uzyskać więcej informacji o kształcie błędu w każdym elemencie.
  • Stosunek czasu składania i czasu procesora rozwiązania : W standardowym MES macierz sztywności jest zwykle montowana szybko, ale jest dość duża. Zazwyczaj rozwiązanie problemu dyskretnego pochłania największą część całkowitego czasu obliczeń. Natomiast macierze sztywności w hp-MES są zwykle dużo mniejsze, ale (dla tego samego rozmiaru macierzy) ich montaż zajmuje więcej czasu niż w standardowym MES. Wynika to głównie z kosztu obliczeniowego kwadratury numerycznej, która musi mieć wyższą precyzję, a zatem musi być wyższego rzędu, w porównaniu ze standardową MES, aby skorzystać z szybszego tempa zbieżności.
  • Wyzwania analityczne : HP-FEM jest ogólnie uważany za trudniejszy do zrozumienia z analitycznego punktu widzenia niż standardowy MES. [ według kogo? ] Dotyczy to wielu technik, takich jak dyskretne zasady maksimum (DMP) dla problemów eliptycznych. Wyniki te stwierdzają, że zwykle przy pewnych ograniczających założeniach dotyczących siatki, aproksymacja MES fragmentarycznie wielomianowa jest zgodna z analogicznymi zasadami maksymalnymi, jak podstawowe eliptyczne PDE. Takie wyniki są bardzo ważne, ponieważ gwarantują, że przybliżenie pozostanie fizycznie dopuszczalne, nie pozostawiając możliwości obliczenia ujemnej gęstości, ujemnego stężenia, czy ujemnej temperatury bezwzględnej. DMP są dość dobrze znane dla MES najniższego rzędu, ale całkowicie nieznane dla hp-FEM w dwóch lub więcej wymiarach. Niedawno sformułowano pierwsze DMP w jednym wymiarze przestrzennym.
  • Wyzwania programistyczne : Zaimplementowanie solwera hp-FEM jest znacznie trudniejsze niż w przypadku standardowego kodu FEM. Liczne problemy, które należy przezwyciężyć, obejmują (ale nie ograniczają się do): formuły kwadraturowe wyższego rzędu, funkcje kształtu wyższego rzędu, informacje o łączności i orientacji dotyczące funkcji kształtu w domenie odniesienia z funkcjami bazowymi w domenie fizycznej itp.

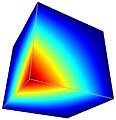
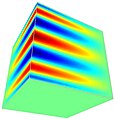
Problem Fichery

Problem Fichery (zwany także problemem narożnika Fichery) jest standardowym problemem wzorcowym dla adaptacyjnych kodów MES. Można go użyć do pokazania dramatycznej różnicy w wydajności standardowego FEM i hp-FEM. Geometria problemu to sześcian z brakującym narożnikiem. Dokładne rozwiązanie ma pojedynczy gradient (analogia nieskończonego naprężenia) w środku. Znajomość rozwiązania dokładnego umożliwia dokładne obliczenie błędu aproksymacji, a tym samym porównanie różnych metod numerycznych. Dla ilustracji problem został rozwiązany przy użyciu trzech różnych wersji adaptacyjnego MES: z elementami liniowymi, elementami kwadratowymi i hp-MES.

  • Fichera problem: singular gradient.

    Problem Fichery: pojedynczy gradient.

  • Fichera problem: convergence comparison.

    Problem Fichery: porównanie zbieżności.

Wykresy zbieżności przedstawiają błąd aproksymacji jako funkcję liczby stopni swobody (DOF). DOF odnosi się do nieznanych parametrów, które są potrzebne do zdefiniowania przybliżenia, a liczba DOF jest równa rozmiarowi macierzy sztywności. Czytelnik może zobaczyć na wykresach, że zbieżność hp-MES jest znacznie szybsza niż zbieżność obu pozostałych metod. Różnica w wydajności jest na tyle duża, że ​​liniowy MES może w ogóle nie być zbieżny (w rozsądnym czasie), a kwadratowy MES wymagałby setek tysięcy, a może milionów DOF, aby osiągnąć dokładność, jaką osiągnął hp-FEM przy około 17 000 DOF. Główną zaletą hp-FEM jest uzyskiwanie bardzo dokładnych wyników przy stosunkowo niewielkiej liczbie stopni swobody.

Wydajność hp-MES

Gładkie funkcje można aproksymować znacznie wydajniej przy użyciu dużych elementów wyższego rzędu niż małych fragmentarycznie liniowych. Ilustruje to poniższy rysunek, na którym jednowymiarowe równanie Poissona z zerowymi warunkami brzegowymi Dirichleta jest rozwiązywane na dwóch różnych siatkach. Dokładnym rozwiązaniem jest funkcja sinus.

  • Po lewej: siatka składająca się z dwóch elementów liniowych.
  • Po prawej: siatka składająca się z jednego elementu kwadratowego.

Piecewise-linear approximation. Quadratic approximation.

Podczas gdy liczba niewiadomych jest taka sama w obu przypadkach (1 DOF), błędy w odpowiedniej normie wynoszą odpowiednio 0,68 i 0,20. Oznacza to, że przybliżenie kwadratowe było mniej więcej 3,5 razy bardziej wydajne niż przybliżenie fragmentarycznie liniowe. Gdy pójdziemy o krok dalej i porównamy (a) cztery elementy liniowe z (b) jednym elementem kwarcowym (p=4), to oba problemy dyskretne będą miały trzy DOF, ale przybliżenie kwarcowe będzie około 40-krotnie bardziej wydajne.

Wręcz przeciwnie, małe elementy niskiego rzędu mogą znacznie lepiej uchwycić cechy małej skali, takie jak osobliwości, niż duże elementy wysokiego rzędu. hp-FEM opiera się na optymalnym połączeniu tych dwóch podejść, co prowadzi do konwergencji wykładniczej. Należy zauważyć, że ta zbieżność wykładnicza jest wyrażona jako oś błędu w stosunku do stopni swobody. W przypadku rzeczywistych aplikacji zwykle bierzemy pod uwagę czas obliczeniowy potrzebny do osiągnięcia tego samego poziomu dokładności. W przypadku tego wskaźnika wydajności udoskonalanie h i hp może zapewnić podobne wyniki, np. patrz ostateczna liczba na (Link do archiwum internetowego). Jak tylko trudniej będzie zaprogramować i zrównoleglić hp-FEM w porównaniu z h-FEM, doskonałość konwergencji udoskonalania hp może stać się niepraktyczna.

Adaptacyjność HP

Niektóre strony FEM opisują adaptacyjność hp jako kombinację adaptacyjności h (rozszczepienie elementów w przestrzeni przy zachowaniu stałego stopnia wielomianu) i adaptacyjności p (tylko zwiększenie ich stopnia wielomianu) [ potrzebne źródło ] . Nie jest to do końca dokładne, ponieważ przystosowanie hp znacznie różni się od przystosowania h i p, ponieważ udoskonalanie hp elementu można wykonać na wiele różnych sposobów. Oprócz prerafinacji element można podzielić w przestrzeni (jak w przypadku adaptacji h), ale istnieje wiele kombinacji stopni wielomianu na elementach podrzędnych. Jest to zilustrowane na rysunku po prawej stronie. Na przykład, jeśli element trójkątny lub czworoboczny jest podzielony na cztery podelementy, w których stopnie wielomianu mogą różnić się co najwyżej o dwa, to daje to 3 ^ 4 = 81 kandydatów do udoskonalenia (nie biorąc pod uwagę kandydatów wielomianowo anizotropowych). Analogicznie, podzielenie sześcianu na osiem podelementów i zmiana ich stopni wielomianu o co najwyżej dwa daje 3^8 = 6561 kandydatów do uściślenia. Standardowe oszacowania błędów FEM zapewniające jedną stałą liczbę na element nie wystarczą, aby kierować automatyczną adaptacją HP.

Funkcje kształtu wyższego rzędu

W standardowym MES pracuje się tylko z funkcjami kształtu związanymi z wierzchołkami siatki (tzw. funkcjami wierzchołków ). W przeciwieństwie do tego, podczas korzystania z hp-FEM, dodatkowo uwzględnia się funkcje krawędziowe (związane z krawędziami elementów), funkcje ścian (odpowiadające powierzchniom elementów – tylko 3D) i funkcje bąbelkowe (wielomiany wyższego rzędu, które znikają na granicach elementów). Poniższe obrazy pokazują te funkcje (ograniczone do jednego elementu):

  • Vertex function.

    Funkcja wierzchołka.

  • Edge function.

    Funkcja krawędzi.

  • Face function.

    Funkcja twarzy.

  • Bubble function.

    Funkcja bąbelków.

Uwaga: wszystkie te funkcje są zdefiniowane w całym wnętrzu elementu.

Otwarte kody hp-FEM

  • Deal.II : Deal.II to bezpłatna biblioteka typu open source do rozwiązywania równań różniczkowych cząstkowych przy użyciu metody elementów skończonych.
  • Koncepcje : biblioteka C/C++ hp-FEM/DGFEM/BEM dla równań eliptycznych opracowana w SAM, ETH Zurich (Szwajcaria) oraz w grupie K. Schmidta w TU Berlin (Niemcy).
  • 2dhp90, 3dhp90: Kody Fortran dla problemów eliptycznych i równania Maxwella opracowane przez L. Demkowicza z ICES, UT Austin.
  • PHAML: równoległy, hierarchiczny, adaptacyjny projekt wielopoziomowy. Oprogramowanie elementów skończonych opracowane w National Institute for Standards and Technology w USA do numerycznego rozwiązywania dwuwymiarowych eliptycznych równań różniczkowych cząstkowych na komputerach równoległych z pamięcią rozproszoną i komputerach wielordzeniowych przy użyciu technik adaptacyjnego udoskonalania siatki i rozwiązań wielosiatkowych.
  • Projekt Hermes : biblioteka C/C++/Python do szybkiego prototypowania adaptacyjnych solwerów HP-FEM z przestrzenią i przestrzenią dla szerokiej gamy systemów PDE i wielofizycznych systemów PDE, opracowana przez grupę hp-FEM z University of Nevada, Reno ( USA), Instytutem Termomechaniki w Pradze (Republika Czeska) oraz Uniwersytetem Zachodnioczeskim w Pilznie (Republika Czeska) – z oprogramowaniem inżynierskim Agros2D zbudowanym na bazie biblioteki Hermes.
  • PHG : PHG to zestaw narzędzi do tworzenia równoległych adaptacyjnych programów elementów skończonych. Nadaje się do h-, p- i hp-fem. PHG jest obecnie aktywnie rozwijany w State Key Laboratory of Scientific and Engineering Computing, Institute of Computational Mathematics and Scientific/Engineering Computing Chińskiej Akademii Nauk (LSEC, CAS, Chiny). PHG zajmuje się zgodnymi siatkami czworościennymi i wykorzystuje bisekcję do adaptacyjnego lokalnego udoskonalania siatki i MPI do przekazywania wiadomości. PHG ma projekt zorientowany obiektowo, który ukrywa szczegóły równoległości i zapewnia wspólne operacje na siatkach i funkcjach elementów skończonych w abstrakcyjny sposób, pozwalając użytkownikom skoncentrować się na swoich algorytmach numerycznych.
  • MoFEM to kod analizy elementów skończonych dostosowany do rozwiązywania problemów multifizycznych z dowolnymi poziomami aproksymacji, różnymi poziomami wyrafinowania siatki i zoptymalizowany pod kątem obliczeń o wysokiej wydajności. Został zaprojektowany, aby móc zarządzać złożonością związaną z heterogenicznym porządkiem przybliżeń dla przestrzeni L2, H1, H-div i H-curl
  • Sparselizard to wielofizyczna, dostosowana do HP, przyjazna dla użytkownika biblioteka elementów skończonych C++ typu open source, obecnie opracowywana na Uniwersytecie w Tampere w Finlandii. Łączy w sobie czworościany 3D i trójkąty/czworokąty 2D, konforemne, adaptacyjne udoskonalanie siatki z hierarchicznymi przestrzeniami funkcyjnymi H1 i H-curl dowolnego porządku dla ogólnego statycznego i przejściowego hp-FEM.

Komercyjne oprogramowanie hp-FEM

  • StressCheck to narzędzie do analizy elementów skończonych z możliwościami hp zorientowanymi na szczegółową analizę strukturalną.
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Hp-FEM&oldid=1111744256 ”