Pierścienie boromejskie

Pierścienie boromejskie
L6a4
Skrzyżowanie nr.	6
Objętość hiperboliczna	7.327724753
kij nr.	9
Notacja Conwaya	.1
Notacja A – B	6 3 2
Thistlethwaite	L6a4
Inne
naprzemienne , hiperboliczne

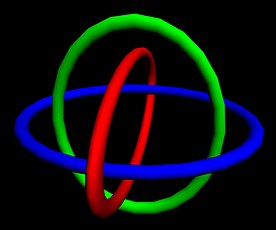
W matematyce pierścienie boromejskie to trzy proste zamknięte krzywe w trójwymiarowej przestrzeni, które są połączone topologicznie i nie można ich od siebie oddzielić, ale które rozpadają się na dwie niepowiązane i niepowiązane pętle, gdy którakolwiek z trzech zostanie przecięta lub usunięta. Najczęściej pierścienie te są rysowane jako trzy koła na płaszczyźnie, na wzór diagramu Venna , naprzemiennie przecinające się nad i pod sobą w punktach, w których się przecinają. Mówi się, że inne trójki krzywych tworzą pierścienie boromejskie, o ile są topologicznie równoważne krzywym przedstawionym na tym rysunku.

Pierścienie boromejskie zostały nazwane na cześć włoskiego rodu Boromeuszów , który używał okrągłego kształtu tych pierścieni jako elementu swojego herbu , ale projekty oparte na pierścieniach boromeńskich były używane w wielu kulturach, w tym przez Normanów i w Japonii . Były używane w symbolice chrześcijańskiej jako znak Trójcy Świętej , a we współczesnym handlu jako logo piwa Ballantine , nadając im alternatywną nazwę pierścieni Ballantine . Fizyczne przypadki pierścieni boromeuszowych zostały utworzone z połączonego DNA lub innych cząsteczek i mają analogi w stanie Efimowa i jądrach boromeuszowych , z których oba mają trzy składniki związane ze sobą, chociaż żadne dwa z nich nie są związane.

Geometrycznie pierścienie boromejskie mogą być realizowane przez połączone elipsy lub (przy użyciu wierzchołków dwudziestościanu foremnego ) przez połączone złote prostokąty . Niemożliwe jest ich zrealizowanie za pomocą okręgów w przestrzeni trójwymiarowej, ale przypuszczano, że można je zrealizować za pomocą kopii dowolnej nieokrągłej prostej zamkniętej krzywej w przestrzeni. W teorii węzłów można udowodnić, że pierścienie boromejskie są połączone, licząc ich n -kolory Foxa . Jako łącza są to brunnowskie , naprzemienne , algebraiczne i hiperboliczne . W topologii arytmetycznej pewne trójki liczb pierwszych mają właściwości łączące analogiczne do pierścieni boromejskich.

Definicja i notacja

W publikacjach matematycznych, które definiują pierścienie boromejskie, często stosuje się diagram połączeń , rysunek krzywych w płaszczyźnie z zaznaczonymi skrzyżowaniami, aby wskazać, która krzywa lub część krzywej przechodzi powyżej lub poniżej na każdym skrzyżowaniu. Taki rysunek można przekształcić w układ krzywych w przestrzeni trójwymiarowej, osadzając płaszczyznę w przestrzeni i deformując narysowane na niej krzywe powyżej lub poniżej osadzonej płaszczyzny na każdym skrzyżowaniu, jak pokazano na schemacie. Powszechnie używany diagram pierścieni boromejskich składa się z trzech równych okręgów wyśrodkowanych w punktach trójkąta równobocznego , wystarczająco blisko siebie, aby ich wnętrza miały wspólne przecięcie (tak jak na diagramie Venna lub trzech okręgach używanych do zdefiniowania trójkąta Reuleaux ). Jego skrzyżowania naprzemiennie znajdują się powyżej i poniżej, gdy są rozpatrywane w kolejności wokół każdego okręgu; innym równoważnym sposobem opisania relacji nad-pod między trzema okręgami jest to, że każdy okrąg przechodzi nad drugim okręgiem na obu ich skrzyżowaniach i pod trzecim okręgiem na obu ich skrzyżowaniach. Mówi się, że dwa ogniwa są równoważne, jeśli zachodzi ciągła deformacja przestrzeni ( izotop otoczenia ) przenosząca się jedno na drugie, a pierścienie Borromeusza mogą odnosić się do dowolnego ogniwa, które jest w tym sensie równoważne ze standardowym diagramem dla tego połączenia.

W The Knot Atlas pierścienie boromejskie są oznaczone kodem „L6a4”; oznaczenie oznacza, że ​​jest to połączenie z sześcioma skrzyżowaniami i naprzemiennym schematem, czwarte z pięciu naprzemiennych połączeń z 6 skrzyżowaniami zidentyfikowanych przez Morwena Thistlethwaite'a na liście wszystkich głównych połączeń z maksymalnie 13 skrzyżowaniami. W tabelach węzłów i linków w książce Dale'a Rolfsena Knots and Links z 1976 roku , rozszerzającej ^.
_{wcześniejsze} zestawienia Alexandra i Briggsa z lat 20 trzy 6-przecinające się 3-składnikowe ogniwa do wyświetlenia. Notacja Conwaya dla pierścieni boromejskich „.1” to skrócony opis standardowego schematu połączeń dla tego łącza.

Historia i symbolika

Valknut na kamieniu Stora Hammars I

Pierścienie boromejskie jako symbol chrześcijańskiej Trójcy , zaadaptowane z rękopisu z XIII wieku

Trzy połączone (ale nie boromejskie) trójkąty we wzorze przedstawionym w świątyni Marundeeswarar

Nazwa „pierścienie boromejskie” pochodzi od użycia tych pierścieni, w postaci trzech połączonych kół, w herbie arystokratycznej rodziny Boromeuszów z północnych Włoch . Samo ogniwo jest znacznie starsze i pojawiło się w postaci valknuta , trzech połączonych trójkątów równobocznych o równoległych bokach, na nordyckich kamieniach wizerunkowych datowanych na VII wiek. Sanktuarium Ōmiwa w Japonii jest również ozdobione motywem pierścieni Borromei w ich konwencjonalnej okrągłej formie. Kamienny filar w VI-wiecznej świątyni Marundeeswarar w Indiach przedstawia trzy równoboczne trójkąty obrócone względem siebie, tworząc regularny enneagram ; podobnie jak pierścienie boromejskie, te trzy trójkąty są połączone, a nie połączone parami, ale ten wzór krzyżowania opisuje inne połączenie niż pierścienie boromejskie.

Powierzchnia Seiferta pierścieni boromejskich

Pierścienie boromejskie były używane w różnych kontekstach, aby wskazać siłę w jedności. W szczególności niektórzy wykorzystali ten projekt jako symbol Trójcy . XIII-wieczny francuski rękopis przedstawiający pierścienie boromejskie oznaczone jako jedność w trójcy zaginął w pożarze w latach czterdziestych XX wieku, ale został odtworzony w książce Adolphe Napoléon Didron z 1843 roku . Didron i inni spekulowali, że opis Trójcy jako trzech równych kręgów w pieśni 33 Raju Dantego był inspirowany podobnymi obrazami, chociaż Dante nie szczegółowo opisuje geometryczny układ tych kręgów. Psychoanalityk Jacques Lacan znalazł inspirację w pierścieniach boromejskich jako modelu dla swojej topologii ludzkiej podmiotowości, przy czym każdy pierścień reprezentuje fundamentalny lacanowski składnik rzeczywistości („rzeczywisty”, „wyimaginowany” i „symboliczny”).

Pierścienie były używane jako logo piwa Ballantine i nadal są używane przez piwo marki Ballantine, obecnie dystrybuowane przez obecnego właściciela marki, firmę Pabst Brewing Company . Z tego powodu czasami nazywano je „pierścieniami Ballantine”.

Pierwszym dziełem z zakresu teorii węzłów , które zawierało pierścienie boromejskie, był katalog węzłów i ogniw opracowany w 1876 roku przez Petera Taita . W matematyce rekreacyjnej pierścienie boromejskie zostały spopularyzowane przez Martina Gardnera , który opisał powierzchnie Seiferta dla pierścieni boromejskich we wrześniu 1961 r. w swojej kolumnie " Mathematical Games " w Scientific American . W 2006 roku Międzynarodowa Unia Matematyczna zdecydowała na 25. Międzynarodowym Kongresie Matematyków w Madrycie w Hiszpanii o użyciu nowego logo opartego na pierścieniach Boromeusza.

Pierścienie częściowe i wielokrotne

W średniowiecznej i renesansowej Europie wiele znaków wizualnych składa się z trzech elementów przeplatających się ze sobą w taki sam sposób, w jaki pierścienie boromejskie są pokazane przeplatane (w ich konwencjonalnym dwuwymiarowym przedstawieniu), ale z pojedynczymi elementami, które nie są zamkniętymi pętlami. Przykładami takich symboli są kamienne rogi Snoldelewa i półksiężyce Diany z Poitiers .

Niektóre łącza oparte na teorii węzłów zawierają wiele konfiguracji pierścieni boromejskich; jedno pięciopętlowe ogniwo tego typu jest używane jako symbol w dyskordianizmie , na podstawie przedstawienia w Principia Discordia .

Właściwości matematyczne

Powiązanie

połączeń algebraicznych dla pierścieni Boromeusza. Pionowa kropkowana czarna linia środkowa to sfera Conwaya dzieląca diagram na 2 sploty .

W teorii węzłów pierścienie boromejskie są prostym przykładem ogniwa brunnowskiego , ogniwa, którego nie można rozdzielić, ale które rozpada się na osobne, niezawiązane pętle, gdy tylko którykolwiek z jego elementów zostanie usunięty. Istnieje nieskończenie wiele ogniw Brunna i nieskończenie wiele trójkrzywych ogniw Brunna, z których najprostsze są pierścienie boromejskie.

Istnieje wiele sposobów sprawdzenia, czy pierścienie boromejskie są ze sobą powiązane. Jednym z nich jest użycie Fox n -colorings , kolorowania łuków diagramu połączeń z liczbami całkowitymi modulo n , tak aby przy każdym skrzyżowaniu dwa kolory na skrzyżowaniu miały taką samą średnią (modulo n ) jak kolor łuku przecinającego się, i tak, aby używane były co najmniej dwa kolory. Liczba kolorowań spełniających te warunki jest niezmiennikiem węzła , niezależnym od schematu wybranego dla ogniwa. Trywialne łącze z trzema składnikami ma $kolorystykę$ , otrzymaną ze standardowego diagramu poprzez wybranie koloru niezależnie dla każdego składnika i odrzucenie kolorowań, które używają tylko $displaystyle n }$ jeden kolor. Z drugiej strony, dla standardowego schematu pierścieni boromejskich, te same pary łuków spotykają się w dwóch przecięciach, zmuszając przecinające się nad nimi łuki, aby miały ten sam kolor, z czego wynika, że ​​jedyne kolory, które spełniają warunki krzyżowania naruszają warunek użycia więcej niż jednego koloru. Ponieważ trywialne ogniwo ma wiele ważnych kolorów, a pierścienie boromejskie nie mają żadnego, nie mogą być równoważne.

Pierścienie boromejskie są naprzemiennymi ogniwami , ponieważ ich konwencjonalny schemat połączeń ma skrzyżowania, które naprzemiennie przechodzą nad i pod każdą krzywą, w kolejności wzdłuż krzywej. Są również ogniwem algebraicznym , ogniwem, które można rozłożyć za pomocą sfer Conwaya na 2 sploty . Są najprostszym naprzemiennym wiązaniem algebraicznym, które nie ma diagramu, który jest jednocześnie naprzemienny i algebraiczny. przypuszczeń Taita wynika , że ​​liczba skrzyżowań pierścieni boromańskich (najmniejsza liczba skrzyżowań na jakimkolwiek z ich diagramów połączeń) wynosi 6, czyli liczba skrzyżowań na ich naprzemiennym diagramie.

Kształt pierścienia

Realizacja pierścieni boromejskich za pomocą elips

Trzy połączone złote prostokąty w regularnym dwudziestościanie

Pierścienie boromejskie są zwykle rysowane z ich pierścieniami wystającymi na okręgi na płaszczyźnie rysunku, ale trójwymiarowe okrągłe pierścienie boromejskie są obiektem niemożliwym : nie jest możliwe utworzenie pierścieni boromeuszowych z okręgów w przestrzeni trójwymiarowej. Mówiąc bardziej ogólnie, Michael H. Freedman i Richard Skora ( 1987 ) udowodnili, używając czterowymiarowej geometrii hiperbolicznej , że żadne ogniwo Brunniana nie może być dokładnie okrągłe. W przypadku trzech pierścieni w ich konwencjonalnym układzie boromeuszowym można to zobaczyć, biorąc pod uwagę schemat połączeń . Jeśli założymy, że dwa z okręgów stykają się w swoich dwóch punktach przecięcia, to leżą one albo w płaszczyźnie, albo w kuli. W obu przypadkach trzeci okrąg musi przejść przez tę płaszczyznę lub kulę cztery razy, nie leżąc w niej, co jest niemożliwe. Inny argument za niemożnością realizacji kołowych, autorstwa Helge Tverberga , wykorzystuje geometrię odwrotną do przekształcenia dowolnych trzech okręgów, tak aby jeden z nich stał się linią, co ułatwia argumentację, że pozostałe dwa koła nie łączą się z nim, tworząc pierścienie boromejskie .

Jednak pierścienie boromejskie można zrealizować za pomocą elips. Można przyjąć, że mają one dowolnie małą ekscentryczność : bez względu na to, jak blisko kołowego może być ich kształt, o ile nie są idealnie okrągłe, mogą tworzyć ogniwa boromejskie, jeśli są odpowiednio ustawione. Urzeczywistnienie pierścieni boromejskich za pomocą trzech wzajemnie prostopadłych złotych prostokątów można znaleźć w dwudziestościanie foremnym , łącząc trzy przeciwległe pary jego krawędzi. Każde trzy niepowiązane wielokąty w przestrzeni euklidesowej można połączyć, po odpowiedniej transformacji skalowania, w celu utworzenia pierścieni boromeuszowych. Jeśli wszystkie trzy wielokąty są płaskie, skalowanie nie jest potrzebne. W szczególności, ponieważ pierścienie boromejskie mogą być zrealizowane przez trzy trójkąty, minimalną możliwą liczbę boków dla każdej z jego pętli, liczba drążków pierścieni boromańskich wynosi dziewięć.

Nierozwiązany problem z matematyki :

Czy istnieją trzy krzywe bez węzłów, a nie wszystkie okręgi, które nie mogą tworzyć pierścieni Boromeusza?

(więcej nierozwiązanych problemów z matematyki)

Mówiąc bardziej ogólnie, Matthew Cook przypuszczał , że dowolne trzy proste, zamknięte krzywe bez węzłów w przestrzeni, a nie wszystkie koła, można połączyć bez skalowania, aby utworzyć pierścienie boromejskie. Po tym, jak Jason Cantarella zasugerował możliwy kontrprzykład, Hugh Nelson Howards osłabił hipotezę, aby zastosować ją do dowolnych trzech płaskich krzywych, z których nie wszystkie są okręgami. Z drugiej strony, chociaż istnieje nieskończenie wiele ogniw Brunna z trzema ogniwami, pierścienie boromejskie są jedynymi, które można utworzyć z trzech wypukłych krzywych.

Długość liny

Logo Międzynarodowej Unii Matematycznej

W teorii węzłów długość liny węzła lub ogniwa jest najkrótszą długością elastycznej liny (o promieniu jeden), która może ją zrealizować. Matematycznie taką realizację można opisać gładką krzywą, której rurowe sąsiedztwo o promieniu jednego promienia unika samoprzecięć. Minimalna długość liny pierścieni boromejskich nie została udowodniona, ale najmniejsza osiągnięta wartość jest realizowana przez trzy kopie płaskiej krzywej z dwoma płatami. Chociaż przypomina wcześniejszego kandydata na minimalną długość liny, zbudowanego z czterech okrągłych łuków o promieniu dwóch, jest nieco zmodyfikowany w stosunku do tego kształtu i składa się z 42 gładkich kawałków zdefiniowanych przez całki eliptyczne , co czyni go krótszym o ułamek procenta niż realizacja fragmentarycznie-kolista. To właśnie ta realizacja, przypuszczalnie mająca na celu zminimalizowanie długości liny, została wykorzystana w Międzynarodowej Unii Matematycznej . Jego długość wynosi ${\ Displaystyle \ około 58,006}$ , podczas gdy najlepiej sprawdzona dolna granica długości to ${\ Displaystyle 12 \ pi \ około 37,699}$ .

W przypadku dyskretnego analogu długości liny, najkrótszej reprezentacji wykorzystującej tylko krawędzie siatki całkowitej , minimalna długość pierścieni Borromeusza wynosi dokładnie ${\ displaystyle 36}$ . Jest to długość reprezentacji za pomocą trzech $dwudziestościan$ prostokątów wpisanych w Jessena w taki sam sposób, jaki reprezentacja za pomocą złotych prostokątów jest wpisana w dwudziestościan foremny

Geometria hiperboliczna

Dopełnienie pierścieni boromejskich, hiperboliczna rozmaitość utworzona z dwóch idealnych ośmiościanów, wielokrotnie widziana na tym widoku . Pierścienie są nieskończenie daleko, w wierzchołkach ośmiościanu.

Pierścienie boromejskie są ogniwem hiperbolicznym : przestrzeń otaczająca pierścienie boromejskie (ich dopełnienie łącznika ) dopuszcza pełną hiperboliczną metrykę skończonej objętości. Chociaż hiperboliczne łącza są obecnie uważane za obfite, pierścienie boromejskie były jednym z najwcześniejszych przykładów, które zostały udowodnione jako hiperboliczne w latach 70 .

Rozmaitości hiperboliczne można rozłożyć kanonicznie na sklejenia wielościanów hiperbolicznych (rozkład Epsteina-Pennera), a dla dopełnienia boromejskiego rozkład ten składa się z dwóch idealnych ośmiościanów foremnych . Objętość dopełnienia boromejskiego wynosi ${\ Displaystyle \ Lambda}$$pi / 4) = 8G \ około 7,32772 \ kropki}$ \ gdzie Λ Funkcja $katalońską$ i jest stałą . Dopełnienie pierścieni Borromeusza jest uniwersalne w tym sensie, że każda zamknięta 3- rozmaitość jest rozgałęzionym pokryciem tej przestrzeni.

Teoria liczb

W topologii arytmetycznej istnieje analogia między węzłami a liczbami pierwszymi , w której bierze się pod uwagę powiązania między liczbami pierwszymi. Trójka liczb pierwszych (13, 61, 937) jest połączona modulo 2 (symbol Rédei to -1), ale jest niepołączona parami modulo 2 ( wszystkie symbole Legendre'a to 1). Dlatego te liczby pierwsze zostały nazwane „właściwymi potrójnymi boromejskimi modulo 2” lub „mod 2 boromejskimi liczbami pierwszymi”.

Realizacje fizyczne

Węzeł pięści małpy jest zasadniczo trójwymiarową reprezentacją pierścieni boromejskich, chociaż w większości przypadków składa się z trzech warstw. Rzeźbiarz John Robinson stworzył dzieła sztuki z trzema trójkątami równobocznymi wykonanymi z blachy , połączonymi w pierścienie boromejskie i przypominającymi trójwymiarową wersję valknuta. Powszechny projekt składanego drewnianego statywu składa się z trzech części wyrzeźbionych z jednego kawałka drewna, przy czym każdy element składa się z dwóch kawałków drewna, nóg i górnej części statywu, połączonych dwoma segmentami drewna otaczającymi wydłużony środkowy dziura w kawałku. Kolejny z trzech elementów przechodzi przez każdy z tych otworów, łącząc trzy elementy razem we wzór pierścieni boromejskich. Trójnogi tej formy opisywano jako pochodzące z rękodzieła indyjskiego lub afrykańskiego.

W chemii molekularne pierścienie boromejskie są molekularnymi odpowiednikami pierścieni boromejskich, które są mechanicznie połączonymi architekturami molekularnymi . W 1997 roku biologowi Chengde Mao i współpracownikom z New York University udało się skonstruować zestaw pierścieni z DNA . W 2003 roku chemik Fraser Stoddart i współpracownicy z UCLA wykorzystali chemię koordynacyjną do skonstruowania zestawu pierścieni w jednym kroku z 18 składników. Borromejskie struktury pierścieniowe zostały użyte do opisania klastrów metali szlachetnych osłoniętych warstwą powierzchniową ligandów tiolanowych. Biblioteka sieci boromejskich została zsyntetyzowana według projektu Giuseppe Resnati i współpracowników poprzez samoorganizację napędzaną wiązaniami halogenowymi . Aby uzyskać dostęp do molekularnego pierścienia boromejskiego składającego się z trzech nierównych cykli, Jay S. Siegel i współpracownicy zaproponowali syntezę krok po kroku.

W fizyce kwantowo-mechaniczny analog pierścieni Borromeusza nazywany jest stanem halo lub stanem Efimowa i składa się z trzech związanych cząstek, które nie są związane parami. Istnienie takich stanów zostało przewidziane przez fizyka Witalija Efimowa w 1970 r. i potwierdzone licznymi eksperymentami rozpoczętymi w 2006 r. Zjawisko to jest ściśle związane z jądrem boromejskim , stabilnym jądrem atomowym składającym się z trzech grup cząstek, które byłyby niestabilne w parach . Inny analog pierścieni Borromeusza w kwantowej teorii informacji obejmuje splątanie trzech kubitów w stanie Greenbergera – Horne – Zeilingera .

• 

  Węzeł pięści małpy

• 

  Molekularne pierścienie boromejskie

Linki zewnętrzne

• Lamb, Evelyn (30 września 2016), „Kilka moich ulubionych przestrzeni: pierścienie boromejskie” , Roots of Unity , Scientific American
• Borromean Olympic Rings ( Brady Haran , 2012), Borromean ribbons ( Tadashi Tokieda , 2016) oraz Neon Knots and Borromean Beer Rings ( Clifford Stoll , 2018), Numberphile
• Pierścienie Borromejskie , Międzynarodowa Unia Matematyczna