Link Brunniański

To czteroskładnikowe ogniwo jest ogniwem brunniańskim.

W teorii węzłów , gałęzi topologii , łącze brunnowskie jest nietrywialnym łączem , które staje się zbiorem trywialnych niepowiązanych okręgów, jeśli usunie się dowolny element. Innymi słowy, przecięcie dowolnej pętli zwalnia wszystkie pozostałe pętle (tak, że żadne dwie pętle nie mogą być bezpośrednio połączone ).

Imię Brunnian pochodzi od Hermanna Brunna . Artykuł Brunna z 1892 r. Über Verkettung zawierał przykłady takich linków.

Przykłady

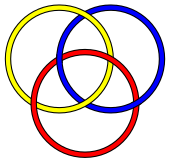
Pierścienie boromejskie to najprostsze ogniwo brunńskie.
Sześcioskładnikowy „gumowy” łącznik Brunnian. Ta sama konstrukcja prowadzi do powiązań brunnowskich z dowolną liczbą elementów.

Najbardziej znanym i najprostszym możliwym łącznikiem brunniańskim są pierścienie boromejskie , połączenie trzech węzłów . Jednak dla każdej liczby trzy lub wyższej istnieje nieskończona liczba powiązań z właściwością Brunniana zawierającą tę liczbę pętli. Oto kilka stosunkowo prostych trójskładnikowych ogniw brunńskich, które nie są tym samym, co pierścienie boromejskie:

  • 12-crossing link.

    12-przekraczający link.

  • 18-crossing link.

    18-skrzyżowanie linku.

  • 24-crossing link.

    24-przekraczający link.

Najprostszym ogniwem brunniańskim, innym niż 6-skrzyżowane pierścienie boromejskie, jest przypuszczalnie 10-skrzyżowane ogniwo L10a140 .

Przykładem n -składnikowego łącza Brunnian jest „gumka” Brunnian Links, w której każdy składnik jest zapętlony wokół następnego jako aba −1 b −1 , przy czym ostatni zapętla się wokół pierwszego, tworząc okrąg.

Nieokrągłość

Niemożliwe jest, aby brunnowskie ogniwo zostało zbudowane z geometrycznych kręgów. Nieco bardziej ogólnie, jeśli połączenie ma tę właściwość, że każdy komponent jest okręgiem i żadne dwa komponenty nie są połączone, to jest trywialne. Dowód, autorstwa Michaela Freedmana i Richarda Skory, osadza trójwymiarową przestrzeń zawierającą łącznik jako granicę modelu kuli Poincarégo czterowymiarowej przestrzeni hiperbolicznej i uwzględnia hiperboliczne wypukłe kadłuby okręgów. Są to dwuwymiarowe podprzestrzenie przestrzeni hiperbolicznej, a ich wzory przecięć odzwierciedlają łączenie parami okręgów: jeśli dwa okręgi są połączone, to ich kadłuby mają punkt przecięcia, ale przy założeniu, że pary okręgów są niepołączone, kadłuby są rozłączne. Biorąc przekroje poprzeczne kuli Poincarégo za pomocą koncentrycznych trójwymiarowych sfer, przecięcie każdej kuli z kadłubami kół jest ponownie ogniwem utworzonym z kół, a ta rodzina przekrojów zapewnia ciągły ruch wszystkich kręgi, które zmniejszają każdy z nich do punktu, nie przecinając żadnego z pozostałych.

Klasyfikacja

Linki brunniańskie zostały sklasyfikowane jako homotopia linków przez Johna Milnora w ( Milnor 1954 ), a niezmienniki, które wprowadził, są teraz nazywane niezmiennikami Milnora.

( n + 1) - składowe łącze Brunniańskie można traktować jako element grupy połączeń - która w tym przypadku (ale nie ogólnie) jest podstawową grupą dopełnienia łącza - n - składowego odłączania, ponieważ przez Brunnianness usunięcie ostatniego linku odłącza pozostałe. Grupa połączeń n -komponentowego rozłączenia jest wolną grupą na n generatorach, F n , ponieważ grupa połączeń pojedynczego połączenia jest grupą węzłów unknot , czyli liczbami całkowitymi, a grupą połączeń niepołączonego związku jest wolny produkt grup linków komponentów.

Nie każdy element grupy łączy daje łącze brunńskie, ponieważ usunięcie dowolnego innego składnika musi również rozłączyć pozostałe n elementów. Milnor wykazał, że elementy grupowe, które odpowiadają powiązaniom Brunna, są powiązane ze stopniowaną algebrą Liego dolnego centralnego szeregu grupy swobodnej, co można interpretować jako „relacje” w wolnej algebrze Liego .

Produkty marki Massey

Główny artykuł: produkt Massey

Powiązania Brunniana można zrozumieć w topologii algebraicznej za pomocą produktów Masseya : produkt Masseya jest produktem n -krotnym, który jest zdefiniowany tylko wtedy, gdy wszystkie ( n - 1)-krotne produkty jego terminów znikają. Odpowiada to właściwości Brunniana polegającej na tym, że wszystkie ( n - 1)-składnikowe łącza podrzędne są rozłączone, ale ogólne łącze n- składnikowe jest połączone nietrywialnie.

Warkocze brunńskie

Zobacz też: Zamknięty warkocz
Standardowym warkoczem jest Brunnian: jeśli usunie się czarne pasmo, niebieskie pasmo jest zawsze na wierzchu czerwonego pasma, a zatem nie są one splecione wokół siebie; podobnie do usuwania innych pasm.

Warkocz brunński to warkocz, który staje się trywialny po usunięciu jednego z jego sznurków. Warkocze brunńskie tworzą podgrupę grupy warkoczy . Warkocze brunńskie na 2- sferze , które nie są brunńskie na 2- kręgu , dają początek nietrywialnym elementom w grupach homotopii 2-sfery. Na przykład „standardowy” warkocz odpowiadający pierścieniom boromejskim daje początek włóknieniu Hopfa S 3 → S 2 , a jego iteracje (jak w codziennym splataniu) są również Brunniańskie.

Przykłady z życia wzięte

Bransoletka z tęczowego krosna przedstawiająca łańcuchy Brunian

Wiele łamigłówek do rozplątywania i niektóre łamigłówki mechaniczne to warianty Brunnian Links, których celem jest uwolnienie pojedynczego elementu tylko częściowo połączonego z resztą, a tym samym demontaż konstrukcji.

Łańcuchy Brunnian są również używane do tworzenia przedmiotów do noszenia i dekoracji z elastycznych pasków za pomocą urządzeń takich jak Rainbow Loom lub Wonder Loom .

  1. ^ Bar-Natan, Dror (2010-08-16). „ Może wszyscy Brunnianie ”, [Myślodsiewnia akademicka] .
  2. ^ Linki brunniańskie „Rubberband”
  3. Bibliografia _ _ Skora, Richard (1987), „Dziwne działania grup na kulach”, Journal of Differential Geometry , 25 : 75–98, doi : 10.4310/jdg/1214440725 ; patrz w szczególności Lemat 3.2, s. 89

Dalsza lektura

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Brunnian_link&oldid=1138585146 ”