Grupa warkoczy

Zwykły warkocz na pięciu pasmach. Każda $się$ dwóch kolejnych elementów .

W matematyce grupa warkoczy na n niciach (oznaczona ), znana również jako grupa warkoczy Artina , to grupa, której elementami są klasy równoważności n - warkoczy (np. W izotopie otoczenia ) , B n $\ displaystyle B_ {n$ i którego grupową operacją jest składanie warkoczy (patrz § Wstęp ). Przykładowe zastosowania grup warkoczy obejmują teorię węzłów , gdzie każdy węzeł może być przedstawiony jako zamknięcie pewnych warkoczy (wynik znany jako twierdzenie Aleksandra ); w fizyce matematycznej , gdzie kanoniczna prezentacja grupy warkoczy przez Artina odpowiada równaniu Yanga-Baxtera (patrz § Podstawowe właściwości ); aw monodromii niezmienniki geometrii algebraicznej .

Wstęp

We wstępie niech n = 4 ; uogólnienie na inne wartości n będzie proste. Rozważmy dwa zestawy czterech przedmiotów leżące na stole, przy czym przedmioty w każdym zestawie są ułożone w linii pionowej i tak, że jeden zestaw znajduje się obok drugiego. (Na poniższych ilustracjach są to czarne kropki.) Za pomocą czterech nici każdy element pierwszego zestawu jest połączony z elementem drugiego zestawu, tak że powstaje zgodność jeden do jednego. Takie połączenie nazywamy warkoczem . Często niektóre pasma będą musiały przechodzić nad lub pod innymi, co ma kluczowe znaczenie: poniższe dwa połączenia to różne warkocze:

jest inny niż

ten sam warkocz uważa się dwa takie połączenia, które mogą wyglądać tak samo przez „ciągnięcie za pasma” :

jest taki sam jak

Wszystkie pasma muszą poruszać się od lewej do prawej; węzły takie jak poniższe nie są uważane za warkocze:

nie jest warkoczem

Można ułożyć dowolne dwa warkocze , rysując pierwszy obok drugiego, wskazując cztery elementy w środku i łącząc odpowiednie pasma:

złożony z

plony

Inny przykład:

złożony z

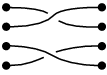
plony

Skład warkoczy σ i τ zapisujemy jako στ .

Zestaw wszystkich warkoczy na czterech pasmach jest oznaczony przez ${\ displaystyle B_ {4}}$ . Powyższa kompozycja warkoczy to rzeczywiście grupowe . Elementem tożsamości jest warkocz składający się z czterech równoległych poziomych pasm, a odwrotność warkocza składa się z tego warkocza, który „cofnie” wszystko, co zrobił pierwszy warkocz, co uzyskuje się przez odwrócenie diagramu takiego jak ten powyżej w poprzek pionowej linii przechodzącej przez jego środek. (Pierwsze dwa przykładowe warkocze powyżej są odwrotnościami).

Aplikacje

Teoria oplotu została ostatnio zastosowana w mechanice płynów , w szczególności w dziedzinie chaotycznego mieszania w przepływach płynów. Splatanie (2 + 1)-wymiarowych trajektorii czasoprzestrzennych utworzonych przez ruch fizycznych prętów, okresowych orbit lub „prętów-widm” oraz prawie niezmiennych zbiorów zostało wykorzystane do oszacowania topologicznej entropii kilku zaprojektowanych i naturalnie występujących układów płynów , poprzez zastosowanie klasyfikacji Nielsena – Thurstona .

Innym obszarem intensywnych badań obejmujących grupy warkoczy i związane z nimi koncepcje topologiczne w kontekście fizyki kwantowej jest teoria i (domniemana) eksperymentalna implementacja tak zwanych anyonów . Mogą one równie dobrze stać się podstawą obliczeń kwantowych z korekcją błędów , dlatego ich abstrakcyjne badanie ma obecnie fundamentalne znaczenie w informacji kwantowej .

Leczenie formalne

Główny artykuł: Przestrzeń konfiguracyjna (matematyka) § Połączenie z grupami plecionek

Aby postawić powyższą nieformalną dyskusję o grupach oplotów na solidnym gruncie, należy użyć koncepcji homotopii topologii algebraicznej , definiując grupy warkoczy jako podstawowe grupy przestrzeni konfiguracyjnej . Alternatywnie, można zdefiniować grupę warkoczy czysto algebraicznie za pomocą relacji warkoczy, pamiętając o obrazach tylko po to, by kierować intuicją.

, $} displaystyle X}$ zredukować grupę warkoczy w sensie Artina do grupy podstawowej, rozważymy połączoną rozmaitość o wymiarze co najmniej 2. $n$ symetryczny kopii $displaystyle$$n}$ iloraz , $iloczyn$ kartezjański przez działanie permutacji $symetrycznej$ na $X$ \ $displaystyle$ } nici operujących na indeksach współrzędnych. Oznacza to, że uporządkowana $krotka$ się na tej samej orbicie , co każda inna, która jest jej ponownie uporządkowaną wersją.

Ścieżka w $krotnie$ jest abstrakcyjnym sposobem omawiania punktów $displaystyle$$X}$ , uważanych za nieuporządkowaną krotkę, niezależnie śledzącą $displaystyle n}$ out ciągów ${\ displaystyle n}$ . Ponieważ $symetrycznego$ wymagać, aby struny nigdy nie przechodziły przez siebie, konieczne jest, abyśmy przeszli do podprzestrzeni $iloczynu$ orbit o różnych punktów . Oznacza $zdefiniowane$${\ Displaystyle 1 \ równoważnik i <j \ równoważnik n}$ usuwamy $podprzestrzenie$ warunki . Jest $jest$$w$ grupie symetrycznej, a ilorazem grupy symetrycznej niewykluczonych . Zgodnie z warunkiem wymiaru zostanie połączony ${\ displaystyle Y} .$

$zdefiniowane$ definicję, możemy nazwać grupę warkoczy ze $( dla dowolnego$$)$ . podstawową grupą punktu bazowego - jest to dobrze aż do izomorfizmu). Przypadek, w którym $euklidesowa$ jest oryginalnym przypadkiem Artina. W niektórych przypadkach można wykazać, że wyższe $grupy$ są trywialne .

Zamknięte warkocze

Zobacz też: warkocz brunński

Gdy X jest płaszczyzną, plecionka może być zamknięta , tj. odpowiednie końce mogą być połączone parami, tworząc łącznik , tj. możliwie splecione połączenie możliwie zawiązanych pętli w trzech wymiarach. Liczba elementów łącza może wynosić od 1 do n , w zależności od permutacji nici określonej przez łącze. Twierdzenie JW Alexandra pokazuje, że każde ogniwo można otrzymać w ten sposób jako "zamknięcie" warkocza. Porównaj z linkami łańcuchowymi .

Różne sploty mogą dać początek temu samemu ogniwu, tak jak różne diagramy skrzyżowań mogą dać początek temu samemu węzłowi . W 1935 roku Andrey Markov Jr. opisał dwa ruchy na diagramach warkoczy, które dają równoważność w odpowiednich zamkniętych warkoczach. Wersja twierdzenia Markowa z jednym ruchem została opublikowana w 1997 roku.

Vaughan Jones pierwotnie zdefiniował swój wielomian jako niezmiennik warkocza, a następnie wykazał, że zależy on tylko od klasy zamkniętego warkocza.

Twierdzenie Markowa podaje warunki konieczne i wystarczające, w których zamknięcia dwóch warkoczy są równoważnymi ogniwami.

Indeks warkocza

„Indeks warkocza” to najmniejsza liczba ciągów potrzebnych do utworzenia zamkniętej reprezentacji warkocza łącza. Jest równa najmniejszej liczbie okręgów Seiferta w dowolnym rzucie węzła.

Historia

Grupy warkoczy zostały wyraźnie wprowadzone przez Emila Artina w 1925 r., Chociaż (jak zauważył Wilhelm Magnus w 1974 r.) Były one już ukryte w pracy Adolfa Hurwitza na temat monodromii z 1891 r.

Grupy warkoczy można opisać za pomocą jawnych prezentacji , jak pokazał Emil Artin w 1947 r. Grupy warkoczy są również rozumiane przez głębszą interpretację matematyczną: jako podstawowa grupa pewnych przestrzeni konfiguracyjnych .

Jak mówi Magnus, Hurwitz przedstawił interpretację grupy warkoczy jako podstawowej grupy przestrzeni konfiguracyjnej (por. Teoria warkoczy ), interpretację, która została utracona z pola widzenia, dopóki nie została ponownie odkryta przez Ralpha Foxa i Lee Neuwirtha w 1962 roku.

Podstawowe właściwości

Generatory i relacje

Rozważ następujące trzy warkocze:

${\ Displaystyle \ sigma _ {1}}$	${\ Displaystyle \ sigma _ {2}}$	${\ Displaystyle \ sigma _ {3}}$

Każdy warkocz w $odwrotności$ zapisać jako kompozycję wielu tych warkoczy i ich Innymi słowy, te trzy warkocze generują grupę ${\ displaystyle B_ {4}}$ . Aby to zobaczyć, dowolny warkocz jest skanowany od lewej do prawej w poszukiwaniu skrzyżowań; $\ sigma _ {i} ^ {- 1}}$ napotka się pasm $Displaystyle$ ja $i + 1}$ lub $}$$}$ jest zapisywana, w zależności od tego, czy nić $}$ się pod, czy nad nicią . ja $\ displaystyle i+1$ . Po dotarciu do prawego końca warkocz został zapisany jako iloczyn $​​{\ displaystyle \ sigma}$ i ich odwrotności.

Jest jasne, że

(i) ${\ Displaystyle \ sigma _ {1} \ sigma _ {3} = \ sigma _ {3} \ sigma _ {1}$ }

podczas gdy następujące dwie relacje nie są tak oczywiste:

(iia) ${\ Displaystyle \ sigma _ {1} \ sigma _ {2} \ sigma _ {1} = \ sigma _ {2} \ sigma _ {1} \ sigma _ {2}}$ ,

(iib) ${\ Displaystyle \ sigma _ {2} \ sigma _ {3} \ sigma _ {2} = \ sigma _ { 3}\sigma _{2}\sigma _{3}}$

(najlepiej te zależności można docenić rysując warkocz na kartce papieru). Można wykazać, że wszystkie inne relacje między warkoczami , $i już$${\ Displaystyle \ sigma _ {2}}$ σ 1 ${1}}$ wynikają z tych relacji i aksjomatów grupowych.

Uogólniając ten przykład na $,$ grupę ${\ displaystyle n}$ abstrakcyjnie zdefiniować za pomocą następującej prezentacji :

${\ Displaystyle B_ { n}=\left\langle \sigma _{1},\ldots ,\sigma _{n-1}\mid \sigma _{i}\sigma _{i+1}\sigma _{i}=\sigma _{i+1}\sigma _{i}\sigma _{i+1},\sigma _{i}\sigma _{j}=\sigma _{j}\sigma _{i}\right\rangle ,}$

$aw$$geq$ relacji, relacji, . Ta prezentacja prowadzi do uogólnień grup plecionek zwanych grupami Artina . Relacje sześcienne, znane jako relacje warkocza , odgrywają ważną rolę w teorii równań Yanga-Baxtera .

Dalsze właściwości

• Grupa warkoczy ${$ trywialna , jest nieskończoną grupą cykliczną i $} 3}}$$\$$Displaystyle$ jest izomorficzna z grupą węzłów węzła koniczyny - w szczególności jest to nieskończona grupa nieabelowa .
• Grupa warkoczy n $się$$1$ jako podgrupa w grupie warkoczy $Displaystyle$ dodając dodatkowe pasmo, które nie przecina żadnego z pierwszych n pasm. Rosnący związek grup warkoczy ze wszystkimi $}$ nieskończona warkoczy ${\ displaystyle B _ {\ infty$ .
• Wszystkie $nieskończony$ nietożsamościowe porządek ; tj $jest$ od skręcania .
• Istnieje niezmienny z $nazwany$ porządek liniowy porządkiem Dehornoya .
• Dla ${\ Displaystyle n \ geq 3}$ , ${\ Displaystyle B_ {n}}$ zawiera podgrupę izomorficzną z grupą swobodną na dwóch generatorach.
• Istnieje homomorfizm zdefiniowany ${\ Displaystyle B_ {n} \ do \ mathbb {Z}}$ zdefiniowany przez σ _ja ↦ 1 . Na przykład warkocz σ ₂ σ ₃ σ ₁ ⁻¹ σ ₂ σ ₃ jest odwzorowany na 1 + 1 − 1 + 1 + 1 = 3 . Ta mapa odpowiada abelianizacji grupy warkoczy. Ponieważ σ _ja ^k ↦ k , to σ _ja ^k jest tożsamością wtedy i tylko wtedy, gdy ${\ displaystyle k = 0}$ . Dowodzi to, że generatory mają nieskończony porządek.

Interakcje

Związek z grupą symetryczną i grupą czystego warkocza

Zapominając, jak pasma skręcają się i krzyżują, każdy warkocz na n pasmach określa permutację na n elementach. To przypisanie jest na i zgodne ze złożeniem, a zatem staje się suriekcyjnym homomorfizmem grupowym B _n → S _n z grupy warkoczowej do grupy symetrycznej . Obraz warkocza σ _i ∈ B _n jest transpozycją s _i = ( i , i +1) ∈ S _n . Te transpozycje generują grupę symetryczną, spełniają relacje grup warkoczyków i mają rząd 2. To przekształca prezentację grupy warkoczyków Artina w prezentację grupy symetrycznej Coxetera:

${\ Displaystyle S_ {n} = \ lewo \ langle s_ {1}, \ ldots, s_ {n-1} | s_ {i} s_ {i + 1} s_ {i} = s_ {i + 1} s_ { i}s_{i+1},s_{i}s_{j}=s_{j}s_{i}{\text{ dla }}|ij|\geq 2,s_{i}^{2}=1 \right\rangle .}$

Jądrem homomorfizmu B _n → S _n jest podgrupa B _n zwana czystą grupą warkoczową na n niciach i oznaczona jako P _n . Można to postrzegać jako podstawową grupę przestrzeni różnych n -krotek płaszczyzny euklidesowej. W czystym warkoczu początek i koniec każdego pasma znajdują się w tej samej pozycji. Czyste grupy warkoczy pasują do krótkiej dokładnej sekwencji

${\ Displaystyle 1 \ do F_ {n-1} \ do P_ {n} \ do P_ {n-1} \ do 1.}$

Ta sekwencja dzieli się i dlatego czyste grupy warkoczy są realizowane jako iterowane półbezpośrednie produkty wolnych grup.

Relacja między B ₃ a grupą modułową

$jest$ centralnym rozszerzeniem grupy modułowej

Grupa oplotów $}$ uniwersalnym centralnym rozszerzeniem grupy modułowej ${\ Displaystyle \ operatorname {PSL} (2, \ mathbb {Z}$ z te siedzą jako kraty wewnątrz (topologicznej) uniwersalnej grupy pokrywającej

${\ Displaystyle {\ overline {\ operatorname {SL} (2, \ mathbb {R}}}} \ do \ operatorname {PSL} (2, \mathbb {R} )}$ .

$\ Displaystyle Z (B_ {3}$ a zatem grupa modułowa jest izomorficzna z ilorazową modulo jej centrum , Z ${$ i równoważnie do grupy automorfizmów wewnętrznych B ${\ Displaystyle B_ {3}$ }

Oto konstrukcja tego izomorfizmu . Definiować

${\ Displaystyle a = \ sigma _ {1} \ sigma _ {2} \ sigma _ {1} \ quad b = \ sigma _ {1} \ sigma_{2}}$ .

Z relacji plecionek wynika, że ​​za $\ displaystyle a ^ {2} = b ^ {3}}$ . Oznaczając ten ostatni produkt jako $,$ to sprawdzić na podstawie relacji oplotu

${\ Displaystyle \ sigma _ {1} c \ sigma _ {1} ^ {- 1} = \ sigma _ {2} c \ sigma _ { 2}^{-1}=c}$

$Displaystyle$ sugeruje, że znajduje się w centrum $B_ {3}}$ . Niech $do$$oznacza$ podgrupę generowaną przez c C _można przyjąć , jest normalna podgrupa ponieważ i ilorazową 3 / _{_} _ _ _ _ _ . Twierdzimy, B ₃ / C ≅ PSL(2, Z ) ; temu izomorfizmowi można nadać wyraźną postać. Współzbiory σ ₁ C i σ ₂ C odwzorowują się na

${\ Displaystyle \ sigma _ {1} C \ mapsto R = {\ rozpocząć {bmatrix} 1 i 1 \\ 0 i 1 \ end{bmatrix}}\qquad \sigma _{2}C\mapsto L^{-1}={\begin{bmatrix}1&0\\-1&1\end{bmatrix}}}$

gdzie L i R to standardowe ruchy w lewo iw prawo na drzewie Sterna – Brocota ; dobrze wiadomo, że ruchy te generują grupę modułową.

Alternatywnie, jedną wspólną prezentacją dla grupy modułowej jest

${\ Displaystyle \ langle v, p \, | \, v ^ {2} = p ^ {3} = 1 \ rangle}$

Gdzie

${\ Displaystyle v = {\ rozpocząć {bmatrix} 0 i 1 \\ - 1 i 0 \ koniec {bmatrix}}, \ qquad p = {\ rozpocząć {bmatrix} 0 i 1 \\ - 1 i 1 \ koniec {bmatrix}}.}$

Odwzorowanie a na v i b na p daje suriekcyjny homomorfizm grupy B ₃ → PSL(2, Z ) .

Środek B ₃ jest równy C , co jest konsekwencją faktu, że c jest w środku, grupa modułowa ma trywialne centrum, a powyższy suriekcyjny homomorfizm ma jądro C .

Stosunek do grupy klas odwzorowania i klasyfikacja warkoczy

grupa oplotów Bn _grupą jest izomorficzna z klas mapowania przebitego dysku z n przebiciami . Najłatwiej jest to zwizualizować, wyobrażając sobie każde nakłucie jako połączone sznurkiem z granicą dysku; każdy homomorfizm odwzorowania, który permutuje dwa przebicia, może być wtedy postrzegany jako homotopia strun, to znaczy splot tych strun.

Dzięki tej interpretacji grup klas mapowania warkoczy, każdy warkocz można sklasyfikować jako okresowy, redukowalny lub pseudo-Anosowa .

Połączenie z teorią węzłów

Jeśli podany jest warkocz i łączy się pierwszą pozycję po lewej stronie z pierwszą po prawej za pomocą nowego sznurka, drugą pozycję po lewej stronie z drugą pozycją po prawej itd. (bez tworzenia warkoczy w nowych ciągach ), uzyskuje się link , a czasem węzeł . Twierdzenie Aleksandra w teorii warkoczy mówi, że odwrotność jest również prawdziwa: każdy węzeł i każde ogniwo powstaje w ten sposób z co najmniej jednego warkocza; taki warkocz można uzyskać przecinając linkę. Ponieważ warkocze można konkretnie podać jako słowa w generatorach σ _i , jest to często preferowana metoda wprowadzania węzłów do programów komputerowych.

Aspekty obliczeniowe

Problem słowny dla relacji warkoczowych jest skutecznie rozwiązywalny i istnieje postać normalna dla elementów B _n pod względem generatorów σ ₁ , ..., σ _{n −1} . (W gruncie rzeczy obliczanie postaci normalnej warkocza jest algebraicznym odpowiednikiem „ciągnięcia nici”, jak pokazano na naszym drugim zestawie obrazów powyżej). System algebry komputerowej GAP może przeprowadzać obliczenia w B _n , jeśli elementy są podane jeśli chodzi o te generatory. Istnieje również pakiet o nazwie CHEVIE dla GAP3 ze specjalną obsługą grup plecionek. Problem słowny jest również skutecznie rozwiązywany za pomocą reprezentacji Lawrence'a-Krammera .

Oprócz problemu tekstowego istnieje kilka znanych trudnych problemów obliczeniowych, które mogłyby implementować grupy warkoczy, zasugerowano zastosowania w kryptografii .

działania

Analogicznie do działania grupy symetrycznej przez permutacje, w różnych układach matematycznych istnieje naturalne działanie grupy warkoczowej na n -krotkach obiektów lub na n -krotnym iloczynie tensorowym , które obejmuje pewne „skręty”. Rozważmy dowolną grupę G i niech X będzie zbiorem wszystkich n -krotek elementów G , których iloczynem jest element identyczności G . Wtedy B _n działa na X w następujący sposób:

${\ Displaystyle \ sigma _ {i} \ lewo (x_ {1}, \ ldots, x_ {i-1}, x_ {i}, x_ {i + 1}, \ ldots, x_ {n} \ prawej) = \left(x_{1},\ldots,x_{i-1},x_{i+1},x_{i+1}^{-1}x_{i}x_{i+1},x_{i +2},\ldkropki,x_{n}\prawo).}$

W ten sposób elementy xi _i xi _{+1 zamieniają x} xi _się miejscami, a ponadto jest przekręcane przez wewnętrzny automorfizm odpowiadający x _{i +1} — zapewnia to, że iloczyn składników pozostaje elementem identyczności. Można sprawdzić, czy warkoczowe relacje grupowe są spełnione i ten wzór rzeczywiście definiuje działanie grupowe B _n na X . Jako inny przykład, pleciona kategoria monoidalna jest kategorią monoidalną z działaniem grupowym oplotu. Takie struktury odgrywają ważną rolę we współczesnej fizyce matematycznej i prowadzą do niezmienników węzłów kwantowych .

Reprezentacje

Elementy grupy plecionek Bn _. można bardziej konkretnie przedstawić za pomocą macierzy Jedną z klasycznych takich reprezentacji jest reprezentacja Burau , w której wpisy macierzy są pojedynczymi zmiennymi wielomianami Laurenta . Od dawna zastanawiano się, czy reprezentacja Burau jest wierna , ale odpowiedź okazała się negatywna dla n ≥ 5 . Mówiąc bardziej ogólnie, głównym otwartym problemem było to, czy grupy warkoczy były liniowe . W 1990 roku Ruth Lawrence opisała rodzinę bardziej ogólnych „reprezentacji Lawrence'a” w zależności od kilku parametrów. W 1996 roku Chetan Nayak i Frank Wilczek stwierdzili, że analogicznie do rzutowych reprezentacji SO(3) , rzutowe reprezentacje grupy plecionek mają fizyczne znaczenie dla niektórych kwazicząstek w ułamkowym kwantowym efekcie hali . Około 2001 roku Stephen Bigelow i Daan Krammer niezależnie udowodnili, że wszystkie grupy plecionek są liniowe. $w$ wykorzystano reprezentację wymiaru Lawrence'a - Krammera zmiennych i $tych$ zmiennych, grupę plecionek zrealizować jako podgrupę ogólnej grupy liniowej liczbami zespolonymi .

Nieskończenie generowane grupy warkoczy

Istnieje wiele sposobów uogólnienia tego pojęcia na nieskończoną liczbę wątków. Najprostszym sposobem jest przyjęcie bezpośredniej granicy grup warkoczy, gdzie dołączone mapy wysyłają n ${\ Displaystyle n-1}$$\ Displaystyle f \ okrężnica B_ {n} \ do B_ {n + 1}}$ generatory ${\ displaystyle B_ {n}}$ do pierwszego ${\ displaystyle n-1}$ generatory ${\ displaystyle B_ {n + 1}}$ (tj. , poprzez dołączenie trywialnego pasma). Jednak ta grupa nie dopuszcza żadnej metryzowalnej topologii, pozostając jednocześnie ciągłą.

Paul Fabel wykazał, że istnieją dwie topologie , które można nałożyć na wynikową grupę, z których każda daje inną grupę. Pierwsza jest bardzo oswojoną grupą i jest izomorficzna z grupą klas mapowania nieskończenie przebijanego dysku — dyskretnym zestawem przebić ograniczających się do granicy dysku .

O drugiej grupie można myśleć tak samo, jak o skończonych grupach warkoczy. Umieść pasmo w każdym z punktów $warkoczy -$ zdefiniowany jako zbiór ścieżek ${\ Displaystyle (0,1/n, 0)}$ do punktów ${\ Displaystyle (0,1/n, 1)}$ tak, że funkcja daje permutację na punktach końcowych - jest izomorficzny z tą dziką grupą. Interesującym faktem jest to, że grupa czystych warkoczy w tej grupie jest izomorficzna zarówno z odwrotną granicą skończonych grup czystych warkoczy, jak iz podstawową grupą sześcianu Hilberta minus zestaw P n $Displaystyle P_ {n}}$

${\ Displaystyle \ {(x_ {i}) _ {i \ in \ mathbb {N}} \ mid x_ {i} = x_ {j} {\ tekst {dla niektórych}} i \ neq j \}.}$

Kohomologia

Zobacz też: Przestrzeń konfiguracyjna (matematyka) § Połączenie z grupami plecionek

Kohomologia grupy jest zdefiniowana jako kohomologia odpowiedniej przestrzeni klasyfikacyjnej Eilenberga-MacLane'a , która jest kompleksem CW jednoznacznie $\ Displaystyle K (G, 1)}$ przez ${$${\ Displaystyle G}$ aż do homotopii. Przestrzeń klasyfikująca dla grupy warkoczy ${\ displaystyle \ mathbb {R}$$n$$konfiguracyjną$ tą nieuporządkowaną ^{przestrzenią} , czyli zbiorem $displaystyle n}$ } różne nieuporządkowane punkty na płaszczyźnie:

$\ mathbb {R} ^ {2}) = \ {\ {u_ {1},...,u_{n}\}:u_{i}\in \mathbb {R} ^{2},u_{i}\neq u_{j}{\text{ for }}i\ neq j\}}$ .

Więc z definicji

${\ Displaystyle H ^ {*} (B_ {n}) = H ^ {*} (K (B_ {n}, 1)) = H ^ {*} (\ nazwa operatora {UConf} _ {n} (\ mathbb {R} ^{2})).}$

Obliczenia współczynników w $)$ Fuks (1970

Podobnie, przestrzeń klasyfikująca dla grupy czystych warkoczy $)}$ { $}$$_ {n} (\ mathbb {R}$ , n- ^ta uporządkowana przestrzeń konfiguracyjna R $\ Displaystyle \ mathbb {R} ^ {2}}$ . W 1968 roku Vladimir Arnold wykazał, że kohomologia całkowa grupy czystych plecionek $wygenerowanej$ algebry zewnętrznej przez zbiór klas pierwszego stopnia ${\ Displaystyle \ omega _ {ij} \; \; 1 \ równoważnik i <j \ równoważnik n}$ , z zastrzeżeniem relacji

${\ Displaystyle \ omega _ {k, \ ell} \ omega _ {\ ell, m} +\omega _{\ell ,m}\omega _{m,k}+\omega _{m,k}\omega _{k,\ell }=0.}$

Zobacz też

• Grupa Artin-Tits
• Kategoria pleciony monoid
• Pleciona przestrzeń wektorowa
• Spleciona algebra Hopfa
• Zmień oprogramowanie do dzwonienia — w jaki sposób oprogramowanie wykorzystuje teorię warkocza do modelowania wzorców dzwonienia
• Teoria węzłów
• Kryptografia nieprzemienna

Dalsza lektura

• Birmańska, Joanna ; Brendle, Tara E. (26 lutego 2005), Warkocze: ankieta , arXiv : math.GT/0409205 . W Menasco i Thistlethwaite 2005
•    Carlucci, Lorenzo; Dehornoy, Patrick ; Weiermann, Andreas (2011), „Wyniki nieudowodnienia z udziałem warkoczy”, Proceedings of the London Mathematical Society , 3, 102 (1): 159–192, arXiv : 0711,3785 , doi : 10,1112/plms/pdq016 , MR 2747726 , S2CID 1646748 7
• Chernavskii, AV (2001) [1994], "Teoria warkocza" , Encyklopedia matematyki , EMS Press
•     DeLigne, Pierre (1972), „Les ImmeUbles des grupes de Tresses Généralisés”, Inventiones Mathematicae , 17 (4): 273–302, Bibcode : 1972inmat..17..273d , doi : 10.1007/BF01406236 , Issn 0020-9910 , MR 0422673 , S2CID 123680847
•   Lis, Ralph ; Neuwirth, Lee (1962), „Grupy warkoczy”, Mathematica Scandinavica , 10 : 119–126, doi : 10,7146/math.scand.a-10518 , MR 0150755
•   Kassel, chrześcijanin; Turaev, Vladimir (2008), Braid Groups , Springer, ISBN 978-0-387-33841-5
•   Menasko, Wilhelm ; Thistlethwaite, Morwen , wyd. (2005), Podręcznik teorii węzłów , Elsevier, ISBN 978-0-444-51452-3

Linki zewnętrzne

• „Grupa warkocza” . Planeta Matematyka .
• Biblioteka obliczeniowa CRyptography and Groups z Centrum Kryptografii Algebraicznej Uniwersytetu Stevensa
• Macauley, M. Wykład 1.3: Grupy w nauce, sztuce i matematyce . Wizualna teoria grup . Uniwersytet Clemsona.
• Bigelow, Stefan . „Eksploracja apletu Java B5” .
• Strona Lipmaa, Helger, Cryptography and Braid Groups , zarchiwizowana z oryginału w dniu 3 sierpnia 2009 r.
• Dalvit, Ester (2015). Warkocze — film .
• Scherich, Nancy. Reprezentacje grup plecionek . Zatańcz swój doktorat . dalej rozwinięty w Za matematyką „Dance Your PhD”, część 1: Grupy warkoczyków.