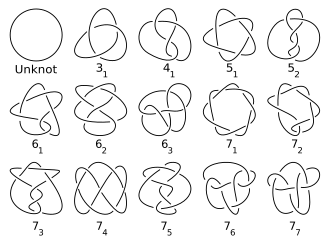
Teoria węzłów

Przykłady różnych węzłów, w tym węzeł trywialny (u góry po lewej) i węzeł koniczyny (poniżej)

Schemat węzła węzła koniczyny, najprostszego nietrywialnego węzła

W matematycznej dziedzinie topologii teoria węzłów jest nauką o węzłach matematycznych . Chociaż inspirowany węzłami , które pojawiają się w życiu codziennym, takimi jak sznurowadła i liny, węzeł matematyczny różni się tym, że końce są połączone, więc nie można go cofnąć, a najprostszym węzłem jest pierścień (lub „nierozwiązany”) . W języku matematycznym węzeł jest osadzeniem koła w trójwymiarowej przestrzeni euklidesowej , ${3}}$ ^ . Dwa węzły matematyczne są $,$ jeśli jeden można przekształcić w drugi poprzez odkształcenie samego siebie (znanego jako izotop otoczenia ) te przekształcenia odpowiadają manipulacjom zawiązanym sznurkiem, które nie obejmują przecinania go ani przepuszczania go przez siebie.

Węzły można opisywać na różne sposoby. Używając różnych metod opisu, może istnieć więcej niż jeden opis tego samego węzła. Na przykład powszechną metodą opisywania węzła jest diagram planarny zwany diagramem węzłów, w którym dowolny węzeł można narysować na wiele różnych sposobów. Dlatego fundamentalnym problemem w teorii węzłów jest ustalenie, kiedy dwa opisy reprezentują ten sam węzeł.

Istnieje kompletne algorytmiczne rozwiązanie tego problemu, którego złożoność jest nieznana . W praktyce węzły są często rozróżniane za pomocą niezmiennika węzła , „ilości”, która jest taka sama, gdy jest obliczana na podstawie różnych opisów węzła. Do ważnych niezmienników należą wielomiany węzłów , grupy węzłów i niezmienniki hiperboliczne.

Pierwotną motywacją twórców teorii węzłów było stworzenie tablicy węzłów i ogniw , czyli węzłów kilku splątanych ze sobą elementów. Od początków teorii węzłów w XIX wieku zestawiono ponad sześć miliardów węzłów i połączeń .

Aby uzyskać więcej informacji, matematycy uogólnili koncepcję węzła na kilka sposobów. Węzły można rozpatrywać w innych przestrzeniach trójwymiarowych i można używać obiektów innych niż koła; patrz węzeł (matematyka) . Na przykład węzeł o wyższych wymiarach jest n -wymiarową kulą osadzoną w ( n +2)-wymiarowej przestrzeni euklidesowej.

Historia

Osobny artykuł: Historia teorii węzłów

Skomplikowany celtycki splot w 1200-letniej Księdze z Kells

Archeolodzy odkryli, że wiązanie węzłów sięga czasów prehistorycznych. Oprócz zastosowań, takich jak zapisywanie informacji i wiązanie przedmiotów, węzły interesują ludzi ze względu na ich estetykę i duchową symbolikę. Węzły pojawiają się w różnych formach chińskiej grafiki pochodzącej z kilku wieków pne (patrz chińskie wiązanie ). Niekończący się węzeł pojawia się w buddyzmie tybetańskim , podczas gdy pierścienie boromejskie wielokrotnie pojawiały się w różnych kulturach, często reprezentując siłę w jedności. Celtycki _ mnisi, którzy stworzyli Księgę z Kells, ozdobili całe strony zawiłymi celtyckimi splotami .

Pierwszy tabulator węzłów, Peter Guthrie Tait

Matematyczna teoria węzłów została po raz pierwszy opracowana w 1771 roku przez Alexandre-Théophile'a Vandermonde'a, który wyraźnie zauważył znaczenie cech topologicznych przy omawianiu właściwości węzłów związanych z geometrią położenia. Matematyczne badania węzłów rozpoczęły się w XIX wieku od Carla Friedricha Gaussa , który zdefiniował całkę łączącą ( Silver 2006 ). XIX wieku teoria Lorda Kelvina, że ​​atomy są węzłami w eterze, doprowadziła Petera Guthriego Taita do stworzenie pierwszych tabel węzłów dla pełnej klasyfikacji. Tait w 1885 roku opublikował tabelę węzłów z maksymalnie dziesięcioma skrzyżowaniami i coś, co stało się znane jako przypuszczenia Taita . Ten zapis zmotywował wczesnych teoretyków węzłów, ale ostatecznie teoria węzłów stała się częścią wyłaniającego się tematu topologii .

Ci topologowie z początku XX wieku — Max Dehn , JW Alexander i inni — badali węzły z punktu widzenia grupy węzłów i niezmienników z teorii homologii , takich jak wielomian Aleksandra . Byłoby to główne podejście do teorii węzłów, dopóki seria przełomów nie zmieniła tematu.

Pod koniec lat 70. William Thurston wprowadził geometrię hiperboliczną do badania węzłów za pomocą twierdzenia o hiperbolizie . Wykazano, że wiele węzłów to węzły hiperboliczne , co umożliwiło wykorzystanie geometrii do zdefiniowania nowych, potężnych niezmienników węzłów . Odkrycie wielomianu Jonesa przez Vaughana Jonesa w 1984 r. ( Sossinsky 2002 , s. 71–89) i późniejsze wkłady Edwarda Wittena , Maxima Kontsevicha i inni ujawnili głębokie powiązania między teorią węzłów a metodami matematycznymi w mechanice statystycznej i kwantowej teorii pola . Od tego czasu wynaleziono mnóstwo niezmienników węzłów, wykorzystując wyrafinowane narzędzia, takie jak grupy kwantowe i homologia Floera .

W ostatnich kilkudziesięciu latach XX wieku naukowcy zainteresowali się badaniem fizycznych węzłów w celu zrozumienia zjawiska wiązania w DNA i innych polimerach. Teorię węzłów można wykorzystać do określenia, czy cząsteczka jest chiralna (ma „ręczność”), czy nie ( Simon 1986 ). Sploty , sznurki, których oba końce są unieruchomione, były skutecznie wykorzystywane do badania działania topoizomerazy na DNA ( Flapan 2000 ). Teoria węzłów może mieć kluczowe znaczenie w konstrukcji komputerów kwantowych, poprzez model topologiczne obliczenia kwantowe ( Collins 2006 ).

Równoważność węzłów

Po lewej węzeł i odpowiadający mu węzeł. Trudniej może być określić, czy złożone węzły, takie jak ten po prawej, są równoważne z nierozwiązanymi.

Węzeł tworzy się rozpoczynając od jednowymiarowego odcinka linii, owijając go arbitralnie wokół siebie, a następnie łącząc ze sobą dwa wolne końce, tworząc zamkniętą pętlę ( Adams 2004 ) ( Sossinsky 2002 ). Po prostu możemy powiedzieć, że węzeł $Krzywa$ „prostą krzywą zamkniętą” (patrz ) - to znaczy: „prawie” iniekcyjną i ciągłą funkcją ${\ Displaystyle K \ okrężnica [0,1] \ do \ mathbb {R} ^ {3}}$ , przy czym jedynym „niewtryskowym” jest ${\ Displaystyle K (0) = K (1)}$ . Topolodzy uważają, że węzły i inne sploty, takie jak ogniwa i sploty, są równoważne, jeśli węzeł można przesuwać płynnie, bez przecinania się, tak aby zbiegł się z innym węzłem.

Idea równoważności węzłów polega na precyzyjnym zdefiniowaniu, kiedy dwa węzły należy uznać za takie same, nawet jeśli są rozmieszczone w przestrzeni w zupełnie inny sposób. Formalna $_ mathbb {R} ^{3}\to \mathbb {R} ^{3}}$ mówi $,$ istnieje zachowujący z ${\ Displaystyle h (K_ {1}) = K_ {2}}$ .

$_ {R} ^{3}\rightarrow \mathbb {R} ^{3}\ \mathrm {for} \ 0\leq t\leq 1\}} przestrzeni na siebie tak, że ostatni z nich niesie$ oznacza pierwszy węzeł na drugi węzeł. (Szczegółowo: dwa węzły i K. $\ Displaystyle K_ {1}}$${\ Displaystyle K_ {2}}$ są równoważne , jeśli istnieje ciągłe odwzorowanie $}$${\ Displaystyle H: \ mathbb {R} ^ {3} \ razy [0,1 ] \$$∈$ {3} takie, że a) dla każdego $x \ in \mathbb {R} ^{3}}$ do ${\ Displaystyle H (x, t) \ in \ mathbb {R} ^ {3}}$ jest homeomorfizmem ${\ Displaystyle \ mathbb {R} ^ {3}} na R 3 {\ Displaystyle \ mathbb {R} ^$ {3} samo; b) ${\ Displaystyle H (x, 0) = x}$ dla wszystkich ${\ Displaystyle x \ in \ mathbb {R} ^ {3}}$ ; oraz c) ${\ Displaystyle H (K_ {1}, 1) = K_ {2}}$ . $.$ funkcja jest znana jako izotop otoczenia )

Te dwa pojęcia równoważności węzłów dokładnie zgadzają się co do tego, które węzły są równoważne: dwa węzły, które są równoważne zgodnie z definicją homeomorfizmu zachowującego orientację, są również równoważne zgodnie z definicją izotopii otoczenia, ponieważ wszelkie homeomorfizmy zachowujące orientację R 3 {\ displaystyle ${ R} ^{3}}$ do samego siebie jest końcowym etapem izotopii otoczenia, zaczynając od tożsamości. I odwrotnie, równoważne dwa węzły zgodnie z definicją izotopii otoczenia są również równoważne zgodnie z definicją homeomorfizmu zachowującego orientację, ponieważ t $\ displaystyle t = 1}$ (końcowy) etap izotopu otoczenia musi być homeomorfizmem zachowującym orientację, przenoszącym jeden węzeł do drugiego.

Podstawowym problemem teorii węzłów, problemem rozpoznawania , jest określenie równoważności dwóch węzłów. Istnieją algorytmy , które rozwiązują ten problem, a pierwszy podał Wolfgang Haken pod koniec lat 60. ( Hass 1998 ). Niemniej jednak algorytmy te mogą być niezwykle czasochłonne, a głównym problemem w teorii jest zrozumienie, jak trudny jest ten problem ( Hass 1998 ). Szczególnie interesujący jest szczególny przypadek rozpoznawania nierozwiązanych węzłów , zwany problemem nierozwiązywanych węzłów ( Hoste 2005). ). W lutym 2021 Marc Lackenby ogłosił nowy algorytm rozpoznawania węzłów, który działa w czasie quasi-wielomianowym .

Schematy węzłów

Przydatnym sposobem wizualizacji węzłów i manipulowania nimi jest rzutowanie węzła na płaszczyznę — pomyśl o węźle rzucającym cień na ścianę. Niewielka zmiana kierunku rzutowania zapewni, że będzie to jeden do jednego, z wyjątkiem podwójnych punktów, zwanych skrzyżowaniami , gdzie „cień” węzła krzyżuje się raz poprzecznie ( Rolfsen 1976 ). Na każdym skrzyżowaniu, aby móc odtworzyć oryginalny węzeł, należy odróżnić splot górny od splotu dolnego. Często robi się to robiąc przerwę w nitce biegnącej pod spodem. Otrzymany diagram jest zanurzoną krzywą płaską z dodatkowymi danymi, które pasmo jest nad, a które pod na każdym skrzyżowaniu. (Diagramy te nazywane są diagramami węzłów , gdy przedstawiają węzeł , i diagramami połączeń , gdy przedstawiają połączenie .) Analogicznie, powierzchnie węzłów w przestrzeni 4 można odnieść do powierzchni zanurzonych w przestrzeni 3.

Diagram zredukowany to diagram węzłów, w którym nie ma skrzyżowań redukowalnych (również skrzyżowań zerowych lub usuwalnych ) lub w którym usunięto wszystkie redukowalne skrzyżowania. Rzut płatkowy to rodzaj występu, w którym zamiast tworzyć podwójne punkty, wszystkie pasma węzła spotykają się w jednym punkcie przecięcia, połączonym z nim pętlami tworzącymi niezagnieżdżone „płatki”.

ruchy Reidemeistera

Główny artykuł: ruch Reidemeistera

W 1927 roku, pracując z tą schematyczną formą węzłów, JW Alexander i Garland Baird Briggs oraz niezależnie Kurt Reidemeister wykazali, że dwa diagramy węzłów należące do tego samego węzła mogą być powiązane sekwencją trzech rodzajów ruchów na diagramie, pokazanym poniżej . Operacje te, zwane teraz ruchami Reidemeistera , to:

1. Skręć i odkręć w dowolnym kierunku.
2. Przesuń jedno pasmo całkowicie nad drugim.
3. Przesuń pasmo całkowicie nad lub pod skrzyżowaniem.

ruchy Reidemeistera

typ I	Typ II
Typ III

Dowód na to, że diagramy równoważnych węzłów są połączone ruchami Reidemeistera, opiera się na analizie tego, co dzieje się w projekcji planarnej ruchu przechodzącego od jednego węzła do drugiego. Ruch można ustawić tak, aby prawie przez cały czas projekcja była diagramem węzłów, z wyjątkiem skończonej liczby przypadków, gdy ma miejsce „zdarzenie” lub „katastrofa”, na przykład gdy więcej niż dwie nici przecinają się w punkcie lub wiele nici stać się styczną w punkcie Dokładna inspekcja pokaże, że skomplikowane zdarzenia można wyeliminować, pozostawiając tylko najprostsze zdarzenia: (1) „załamanie” tworzące się lub prostowane; (2) dwie nici stają się styczne w punkcie i przechodzą przez nie; oraz (3) trzy pasma przecinające się w jednym punkcie. To są właśnie ruchy Reidemeistera ( Sossiński 2002 , rozdz. 3) ( Lickorish 1997 , rozdz. 1).

Niezmienniki węzłów

Wydruk 3D przedstawiający dopełnienie ósemki autorstwa François Guéritaud, Saula Schleimera i Henry'ego Segermana

Główny artykuł: niezmiennik węzła

Niezmiennikiem węzła jest „ilość”, która jest taka sama dla równoważnych węzłów ( Adams 2004 ) ( Lickorish 1997 ) ( Rolfsen 1976 ). Na przykład, jeśli niezmiennik jest obliczany na podstawie diagramu węzłów, powinien dawać tę samą wartość dla dwóch diagramów węzłów reprezentujących równoważne węzły. Niezmiennik może przyjąć tę samą wartość na dwóch różnych węzłach, więc sam może nie być w stanie rozróżnić wszystkich węzłów. Elementarnym niezmiennikiem jest trójkolorowość .

„Klasyczne” niezmienniki węzłów obejmują grupę węzłów , która jest podstawową grupą dopełnienia węzła , oraz wielomian Aleksandra , który można obliczyć z niezmiennika Aleksandra, modułu zbudowanego z nieskończonego cyklicznego pokrycia dopełnienia węzła ( Lickorish 1997 ) ( Rolfsen 1976 ). Pod koniec XX wieku niezmienniki, takie jak wielomiany węzłów „kwantowych”, niezmienniki Vassilieva i odkryto niezmienniki hiperboliczne. Te wyżej wymienione niezmienniki to tylko wierzchołek góry lodowej współczesnej teorii węzłów.

Wielomiany węzłów

Główny artykuł: wielomian węzłów

Wielomian węzła jest niezmiennikiem węzła , który jest wielomianem . Dobrze znane przykłady obejmują Jonesa i Alexandra . Wariant wielomianu Aleksandra, wielomian Alexandra-Conwaya , jest wielomianem w zmiennej z ze współczynnikami całkowitymi ( Lickorish 1997 ).

Wielomian Alexandra-Conwaya jest w rzeczywistości zdefiniowany w kategoriach powiązań , które składają się z jednego lub więcej splątanych ze sobą węzłów. Koncepcje wyjaśnione powyżej dla węzłów, np. diagramy i ruchy Reidemeistera, dotyczą również połączeń.

Rozważmy zorientowany diagram połączeń, tj. taki, w którym każdy element łącza ma preferowany kierunek wskazany strzałką. Dla danego skrzyżowania diagramu niech będą zorientowanymi diagramami połączeń wynikającymi ze zmiany diagramu, jak pokazano na rysunku: ${\ Displaystyle L_ {+}, L_ {-}, L_ {0}}$

Oryginalny diagram może być albo $,$$wybranego$ konfiguracji . Następnie wielomian Alexandra – Conwaya jest definiowany rekurencyjnie zgodnie z regułami: do ( $\ displaystyle C (z)$

• ${\ Displaystyle C (O) = 1}$ (gdzie dowolnym schematem węzła ) O $\ Displaystyle O}$
• ${\ Displaystyle C (L_ {+}) = C (L_ {-}) + zC (L_ {0}).}$

Drugą zasadą jest to, co jest często określane jako relacja motków . Aby sprawdzić, czy te reguły dają niezmiennik zorientowanego łącza, należy ustalić, że wielomian nie zmienia się pod wpływem trzech ruchów Reidemeistera. W ten sposób można zdefiniować wiele ważnych wielomianów węzłów.

Poniżej znajduje się przykład typowego obliczenia z wykorzystaniem relacji pasm. Oblicza wielomian Alexandra-Conwaya węzła koniczyny . Żółte plamy wskazują, gdzie stosowana jest zależność.

do ( ) = do ( ) + z do ( )

daje unknot i link Hopf . Zastosowanie relacji do łącza Hopfa tam, gdzie wskazano,

do ( ) = do ( ) + z do ( )

daje połączenie deformowalne do jednego z 0 przecięciami (w rzeczywistości jest to rozłączenie dwóch komponentów) i węzła. Odłączenie wymaga trochę podstępu:

do ( ) = do ( ) + z do ( )

co implikuje, że C (rozłączenie dwóch składowych) = 0, ponieważ pierwsze dwa wielomiany są z węzła, a zatem są równe.

Połączenie tego wszystkiego pokaże:

${\ Displaystyle C (\ operatorname {koniczyna}) = 1 + z (0 + z) = 1 + z ^ {2 }}$

Ponieważ wielomian Alexandra-Conwaya jest niezmiennikiem węzła, pokazuje to, że koniczyna nie jest równoważna z nierozwiązanym. Tak więc koniczynka jest naprawdę „zawiązana”.

• 

  Lewy węzeł koniczyny.

• 

  Węzeł koniczyny prawoskrętnej.

W rzeczywistości istnieją dwa sęki koniczyny, zwane prawostronnymi i lewoskrętnymi koniczynami, które są swoimi lustrzanymi odbiciami (weź schemat trójliści podany powyżej i zmień każde skrzyżowanie w drugą stronę, aby uzyskać lustrzane odbicie). Nie są one sobie równoważne, co oznacza, że ​​nie są amfichiralne. Zostało to pokazane przez Maxa Dehna , przed wynalezieniem wielomianów węzłowych, przy użyciu metod teorii grup ( Dehn 1914 ). Ale wielomian Alexandra-Conwaya dla każdego rodzaju koniczyny będzie taki sam, co można zobaczyć, przechodząc przez powyższe obliczenia z lustrzanym odbiciem. Jones _ wielomian może w rzeczywistości rozróżnić lewoskrętne i prawoskrętne sęki koniczyny ( Lickorish 1997 ).

Niezmienniki hiperboliczne

William Thurston udowodnił, że wiele węzłów to węzły hiperboliczne , co oznacza, że ​​dopełnienie węzła (tj. zbiór punktów przestrzeni 3 poza węzłem) dopuszcza strukturę geometryczną, w szczególności geometrię hiperboliczną . Struktura hiperboliczna zależy tylko od węzła, więc każda wielkość obliczona na podstawie struktury hiperbolicznej jest niezmiennikiem węzła ( Adams 2004 ).

Pierścienie boromejskie są łącznikiem z właściwością, że usunięcie jednego pierścienia rozłącza pozostałe.

Widok wierzchołka SnapPea : pierścienie boromejskie uzupełniają się z perspektywy mieszkańca mieszkającego w pobliżu czerwonego komponentu.

Geometria pozwala nam wizualizować, jak wygląda wnętrze węzła lub dopełnienia ogniwa, wyobrażając sobie promienie światła przemieszczające się wzdłuż geodezji geometrii . Przykładem jest rysunek dopełnienia pierścieni boromejskich . Mieszkaniec tego dopełnienia linku ogląda przestrzeń z okolic czerwonego komponentu. Kule na zdjęciu to rzuty horoballa okolice łącza. Pogrubiając ogniwo w standardowy sposób uzyskuje się horoballowe sąsiedztwa elementów ogniwa. Mimo że granica sąsiedztwa jest torusem, patrząc od wewnątrz dopełnienia łącza, wygląda jak kula. Każdy element łącza przedstawia nieskończenie wiele kul (jednego koloru), ponieważ istnieje nieskończenie wiele promieni świetlnych od obserwatora do elementu łącza. Podstawowy równoległobok (pokazany na rysunku) układa się pionowo i poziomo i pokazuje, jak rozciągać wzór sfer w nieskończoność.

Ten wzór, wzór horoball, sam w sobie jest użytecznym niezmiennikiem. Inne niezmienniki hiperboliczne obejmują kształt podstawowego równoległoboku, długość najkrótszej geodezyjnej i objętość. Nowoczesne metody tworzenia tabel węzłów i połączeń skutecznie wykorzystywały te niezmienniki. Szybkie komputery i sprytne metody uzyskiwania tych niezmienników sprawiają, że obliczenie tych niezmienników jest w praktyce prostym zadaniem ( Adams, Hildebrand & Weeks 1991 ).

Wyższe wymiary

Węzeł w trzech wymiarach można rozwiązać, umieszczając go w przestrzeni czterowymiarowej. Odbywa się to poprzez zmianę skrzyżowań. Załóżmy, że jedno pasmo znajduje się za drugim, patrząc z wybranego punktu. Podnieś go do czwartego wymiaru, aby nie było przeszkód (przednie pasmo nie ma tam żadnego elementu); następnie przesuń go do przodu i upuść z powrotem, teraz z przodu. Analogią dla samolotu byłoby podniesienie sznurka z powierzchni lub usunięcie kropki z wnętrza koła.

W rzeczywistości, w czterech wymiarach, każda nie przecinająca się zamknięta pętla jednowymiarowego łańcucha jest równoważna niepunktowi. Najpierw „pchnij” pętlę w trójwymiarową podprzestrzeń, co zawsze jest możliwe, choć techniczne do wyjaśnienia.

Przestrzeń czterowymiarowa występuje jednak w klasycznej teorii węzłów, a ważnym tematem jest badanie węzłów plasterkowych i węzłów wstążkowych . Znany otwarty problem polega na pytaniu, czy każdy węzeł plastra jest również wstążką.

Wiązanie sfer o wyższym wymiarze

$za$ jednowymiarową kulę, następnym uogólnieniem jest rozważenie dwuwymiarowej kuli ${\ Displaystyle \ mathbb {R} ^ {4}}$ ) osadzonej w 4-wymiarowej przestrzeni euklidesowej ( ). Takie osadzenie jest zawiązane, jeśli nie ma homeomorfizmu ${\ Displaystyle \ mathbb {R} ^ {4}}$ na siebie, przenosząc osadzoną 2-sferę do standardowego „okrągłego” osadzania 2-sfery. Sęki zawieszone i sęki przędzone to dwie typowe rodziny takich sęków 2-sferycznych.

Technika matematyczna zwana „położeniem ogólnym” implikuje, że dla danej n -sfery w m -wymiarowej przestrzeni euklidesowej, jeśli m jest wystarczająco duże (w zależności od n ), sfera powinna być nierozwiązana. Ogólnie rzecz biorąc, odcinkowo-liniowe n -sfery tworzą węzły tylko w ( n + 2)-wymiarowej przestrzeni ( Zeeman 1963 ), chociaż nie jest to już wymagane w przypadku kul z płynnymi węzłami. W rzeczywistości są gładko zawiązane ${\ Displaystyle (4k-1)}$ - kule w 6 k -wymiarowej przestrzeni; np. w ( $)$ ) ( Levine 1965 jest gładko zawiązana 3-kula . Zatem współwymiar gładkiego węzła może być dowolnie duży, gdy nie ustala się wymiaru zawiązanej kuli; jednak k $osadzona$ w k ${\ Displaystyle 2n-3k-3> 0}$ jest nierozwiązany. Pojęcie węzła ma dalsze uogólnienia w matematyce, patrz: Knot (matematyka) , izotopowa klasyfikacja osadzeń .

$Każdy$ węzeł w n -sferze jest ogniwem zbioru ${n +1}}$ rzeczywistego z izolowaną osobliwością w ( Akbulut i King 1981 ).

n -węzeł to pojedynczy osadzony w $}$$mathbb {R} ^ {m}$ { \ displaystyle N -łącze $się$ z k -kopii w , $jest$ k liczbą . _ m $2}$ a $_$$zbadane$ dobrze _

Dodawanie węzłów

Główny artykuł: suma węzłów

Dodanie dwóch węzłów

Dwa węzły można dodać, przecinając oba węzły i łącząc pary końcówek. Operacja nazywana jest sumą węzłów lub czasami połączoną sumą lub złożeniem dwóch węzłów. Można to formalnie zdefiniować w następujący sposób ( Adams 2004 ): rozważ płaską projekcję każdego węzła i załóż, że te projekcje są rozłączne. Znajdź prostokąt w płaszczyźnie, w której jedna para przeciwległych boków jest łukami wzdłuż każdego węzła, podczas gdy reszta prostokąta jest rozłączna z węzłami. Utwórz nowy węzeł, usuwając pierwszą parę przeciwległych boków i łącząc drugą parę przeciwległych boków. Wynikowy węzeł jest sumą oryginalnych węzłów. W zależności od tego, jak to zostanie zrobione, mogą powstać dwa różne węzły (ale nie więcej). Ta niejednoznaczność sumy może zostać wyeliminowana w odniesieniu do węzłów jako zorientowane , tj. posiadające preferowany kierunek przemieszczania się wzdłuż węzła i wymagające, aby łuki węzłów w sumie były zorientowane zgodnie z zorientowaną granicą prostokąta.

Suma węzłów zorientowanych węzłów jest przemienna i asocjacyjna . Węzeł jest liczbą pierwszą , jeśli jest nietrywialny i nie może być zapisany jako suma węzłów dwóch nietrywialnych węzłów. Węzeł, który można zapisać jako taką sumę, jest złożony . Istnieje rozkład liczb pierwszych dla węzłów, analogiczny do pierwszych i złożonych ( Schubert 1949 ). W przypadku węzłów zorientowanych ten rozkład jest również wyjątkowy. Można również dodawać sęki o wyższych wymiarach, ale istnieją pewne różnice. Chociaż nie możesz utworzyć węzła w trzech wymiarach, dodając dwa nietrywialne węzły, możesz to zrobić w wyższych wymiarach, przynajmniej jeśli weźmie się pod uwagę gładkie sęki w kowymiarze co najmniej 3.

Tabulowanie węzłów

Zobacz także: Lista głównych węzłów i tabela węzłów

Tabela głównych węzłów do siedmiu skrzyżowań. Węzły są oznaczone notacją Alexandra-Briggsa

Tradycyjnie sęki były katalogowane pod względem liczby skrzyżowań . Tabele węzłów na ogół zawierają tylko główne sęki i tylko jeden wpis dla węzła i jego lustrzanego odbicia (nawet jeśli są różne) ( Hoste, Thistlethwaite & Weeks 1998 ). Liczba nietrywialnych węzłów o danej liczbie skrzyżowań gwałtownie wzrasta, co utrudnia obliczenia w postaci tabelarycznej ( Hoste 2005 , s. 20). Wysiłki tabelaryczne doprowadziły do ​​wyliczenia ponad 6 miliardów węzłów i połączeń ( Hoste 2005 , P. 28). Ciąg liczby węzłów pierwszych danego numeru skrzyżowania, aż do numeru skrzyżowania 16, wynosi 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46 972 , 253 293 , 1 388 705 ... (sekwencja A002863 w OEIS ). Chociaż znane są wykładnicze górne i dolne granice tego ciągu, nie zostało udowodnione, że ten ciąg jest ściśle rosnący ( Adams 2004 ).

Pierwsze tabele węzłów autorstwa Taita, Little'a i Kirkmana wykorzystywały diagramy węzłów, chociaż Tait również używał prekursora notacji Dowkera . Dla węzłów wymyślono różne notacje, które umożliwiają bardziej wydajną tabelaryzację ( Hoste 2005 ).

Wczesne tabele próbowały wymienić wszystkie węzły z co najwyżej 10 skrzyżowań i wszystkie naprzemienne węzły z 11 skrzyżowań ( Hoste, Thistlethwaite & Weeks 1998 ). Rozwój teorii węzłów dzięki Alexandrowi, Reidemeisterowi, Seifertowi i innym ułatwił zadanie weryfikacji, a tabele węzłów do 9 skrzyżowań włącznie zostały opublikowane przez Alexandra – Briggsa i Reidemeistera pod koniec lat dwudziestych XX wieku.

Pierwszej poważnej weryfikacji tej pracy dokonał w latach 60. John Horton Conway , który nie tylko opracował nową notację, ale także wielomian Alexandra-Conwaya ( Conway 1970 ) ( Doll & Hoste 1991 ). W ten sposób zweryfikowano listę węzłów maksymalnie 11 skrzyżowań oraz nową listę powiązań do 10 skrzyżowań. Conway znalazł szereg pominięć, ale tylko jedno powtórzenie w tabelach Tait-Little; jednak przegapił duplikaty zwane parą Perko , które zostały zauważone dopiero w 1974 roku przez Kennetha Perko ( Perko 1974 ). Ten słynny błąd rozpowszechnił się, gdy Dale Rolfsen dodał tabelę węzłów do swojego wpływowego tekstu, opartego na pracy Conwaya. Artykuł Conwaya z 1970 r. Na temat teorii węzłów zawiera również powielenie typograficzne na swojej stronie z 11 przecinającymi się węzłami bez zmiany i pomija 4 przykłady - 2 wymienione wcześniej w pracy magisterskiej D. Lombardero z Princeton z 1968 r. I 2 kolejne odkryte później przez Alaina Caudrona. [patrz Perko (1982), Primality of some knots, Topology Proceedings] Mniej znany jest duplikat w jego tablicy 10 skrzyżowań: 2.-2.-20.20 jest zwierciadłem 8*-20:-20. [Patrz Perko (2016), Historyczne punkty niecyklicznej teorii węzłów, J. Knot Theory Ramifications].

Pod koniec lat 90. Hoste, Thistlethwaite i Weeks zestawiono wszystkie węzły w 16 skrzyżowaniach ( Hoste, Thistlethwaite i Weeks 1998 ). W 2003 r. Rankin, Flint i Schermann sporządzili zestawienie naprzemiennych węzłów w 22 skrzyżowaniach ( Hoste 2005 ). W 2020 roku Burton zestawił wszystkie główne węzły z maksymalnie 19 skrzyżowaniami ( Burton 2020 ).

Notacja Alexandra-Briggsa

Jest to najbardziej tradycyjny zapis, ze względu na artykuł Jamesa W. Alexandra i Garlanda B. Briggsa z 1927 r., A później rozszerzony przez Dale'a Rolfsena w jego tabeli węzłów (patrz obrazek powyżej i Lista głównych węzłów ). Notacja po prostu organizuje węzły według ich numeru skrzyżowania. Numer skrzyżowania zapisuje się z indeksem dolnym, aby wskazać jego kolejność wśród wszystkich węzłów z tym numerem skrzyżowania. Ta kolejność jest dowolna i dlatego nie ma specjalnego znaczenia (chociaż w każdej liczbie skrzyżowań węzeł skrętu następuje po węźle torusa ). Linki są zapisywane przez numer skrzyżowania z indeksem górnym oznaczającym liczbę elementów i indeksem dolnym oznaczającym ich kolejność w połączeniach o tej samej liczbie elementów i skrzyżowań. Tak więc węzeł koniczyny jest zapisany jako 3 ₁ , a połączenie Hopfa to 2
² ₁ . Nazwy Alexandra – Briggsa z zakresu od 10 ₁₆₂ do 10 ₁₆₆ są niejednoznaczne ze względu na odkrycie pary Perko u Charlesa Newtona Little'a oryginalne i późniejsze tabele węzłów oraz różnice w podejściu do korygowania tego błędu w tabelach węzłów i innych publikacjach powstałych po tym punkcie.

Notacja Dowkera-Thistlethwaite'a

Główny artykuł: notacja Dowkera-Thistlethwaite'a

Diagram węzłów ze skrzyżowaniami oznaczonymi dla sekwencji Dowkera

Notacja Dowkera-Thistlethwaite'a , zwana także notacją lub kodem Dowkera, dla węzła jest skończoną sekwencją parzystych liczb całkowitych. Liczby są generowane przez podążanie za węzłem i oznaczanie skrzyżowań kolejnymi liczbami całkowitymi. Ponieważ każde skrzyżowanie jest odwiedzane dwukrotnie, tworzy to parzyste liczby całkowite z nieparzystymi liczbami całkowitymi. Odpowiedni znak jest podany w celu wskazania nad i pod skrzyżowaniem. Na przykład na tym rysunku diagram węzłów ma skrzyżowania oznaczone parami (1,6) (3,−12) (5,2) (7,8) (9,−4) i (11,−10). Notacja Dowkera-Thistlethwaite'a dla tego oznaczenia to sekwencja: 6, -12, 2, 8, -4, -10. Diagram węzłów ma więcej niż jedną możliwą notację Dowkera, a podczas rekonstrukcji węzła z notacji Dowkera-Thistlethwaite'a istnieje dobrze zrozumiała niejednoznaczność.

Notacja Conwaya

Główny artykuł: notacja Conwaya (teoria węzłów)

Notacja Conwaya dla węzłów i połączeń, nazwana na cześć Johna Hortona Conwaya , jest oparta na teorii splotów ( Conway 1970 ). Zaletą tej notacji jest to, że odzwierciedla ona niektóre właściwości węzła lub ogniwa.

Notacja opisuje sposób konstruowania określonego diagramu łącza. Zacznij od podstawowego wielościanu , 4-wartościowego połączonego grafu planarnego bez obszarów dwukątnych . Taki wielościan jest oznaczony najpierw liczbą wierzchołków, a następnie liczbą gwiazdek, które określają pozycję wielościanu na liście wielościanów podstawowych. Na przykład 10** oznacza drugi wielościan z 10 wierzchołkami na liście Conwaya.

Każdy wierzchołek ma następnie podstawiony splot algebraiczny (każdy wierzchołek jest zorientowany, więc nie ma arbitralnego wyboru w podstawieniu). Każdy taki splot posiada oznaczenie składające się z cyfr oraz znaków + lub −.

Przykładem jest 1*2 −3 2. 1* oznacza jedyny podstawowy wielościan o 1 wierzchołku. 2 −3 2 to ciąg opisujący ułamek ciągły związany z wymierną plątaniną . Wstawia się ten splot w wierzchołku podstawowego wielościanu 1*.

Bardziej skomplikowanym przykładem jest 8*3.1.2 0.1.1.1.1.1 Tutaj znowu 8* odnosi się do podstawowego wielościanu z 8 wierzchołkami. Kropki oddzielają zapis dla każdej splotu.

Każdy link dopuszcza taki opis i jasne jest, że jest to bardzo zwarta notacja nawet dla bardzo dużej liczby skrzyżowań. Zwykle używane są dalsze skróty. Ostatni przykład jest zwykle zapisywany 8*3:2 0, gdzie jedynki są pomijane i zachowana jest liczba kropek z wyjątkiem kropek na końcu. W przypadku węzła algebraicznego, takiego jak w pierwszym przykładzie, często pomija się 1*.

Pionierski artykuł Conwaya na ten temat zawiera do 10-wierzchołkowych podstawowych wielościanów, których używa do zestawiania połączeń, które stały się standardem dla tych łączy. Aby uzyskać dalszą listę wielościanów o wyższych wierzchołkach, dostępne są niestandardowe opcje.

Kod Gaussa

Główny artykuł: kod Gaussa

Kod Gaussa , podobny do notacji Dowkera-Thistlethwaite'a, reprezentuje węzeł z sekwencją liczb całkowitych. Jednak zamiast każdego skrzyżowania są reprezentowane przez dwa różne numery, skrzyżowania są oznaczone tylko jednym numerem. Gdy skrzyżowanie jest skrzyżowaniem, wyświetlana jest liczba dodatnia. Na skrzyżowaniu, liczba ujemna. Na przykład węzeł koniczyny w kodzie Gaussa można podać jako: 1,−2,3,−1,2,−3

Kod Gaussa ma ograniczoną zdolność do identyfikowania węzłów. Ten problem jest częściowo rozwiązany przez rozszerzony kod Gaussa .

Zobacz też

• Geometria kontaktu # Legendarne podrozmaitości i węzły
• Węzły i wykresy
• Lista tematów teorii węzłów
• Węzeł molekularny
• Topologia kwantowa
• Teoria wstążki
• Krawat § Rodzaje węzłów
• Sztuczka z kablem do lampy

Źródła

•   Adams, Colin (2004), The Knot Book: elementarne wprowadzenie do matematycznej teorii węzłów , American Mathematical Society , ISBN 978-0-8218-3678-1
•    Adams, Colin; Crawford, Thomas; DeMeo, Benjamin; Landry, Michael; Lin, Alex Tong; Montee, MurphyKate; Park, Seojung; Venkatesh, Saraswati; Yhee, Farrah (2015), „Projekcje węzłów z pojedynczym wielokrotnym skrzyżowaniem”, Journal of Knot Theory and Its Ramifications , 24 (3): 1550011, 30, arXiv : 1208,5742 , doi : 10,1142/S021821651550011X , MR 3342136 , S2CID 119320887
•   Adams, Colin; Hildebrand, Marcin; Weeks, Jeffrey (1991), „Niezmienniki hiperboliczne węzłów i linków”, Transactions of the American Mathematical Society , 326 (1): 1–56, doi : 10.1090 / s0002-9947-1991-0994161-2 , JSTOR 2001854
•   Akbulut, Selman ; King, Henry C. (1981), „Wszystkie węzły są algebraiczne”, Comm. Matematyka Helv. , 56 (3): 339–351, doi : 10.1007/BF02566217 , S2CID 120218312
• Bar-Natan, Dror (1995), „O niezmiennikach węzła Wasiliewa”, Topologia , 34 (2): 423–472, doi : 10.1016 / 0040-9383 (95) 93237-2
• Burton, Benjamin A. (2020). „Następne 350 milionów węzłów” . 36. Międzynarodowe Sympozjum Geometrii Obliczeniowej (SoCG 2020) . Leibniz Int. proc. Poinformować. Tom. 164. Schloss Dagstuhl–Leibniz-Zentrum für Informatik. s. 25:1–25:17. doi : 10.4230/LIPIcs.SoCG.2020.25 .
•   Collins, Graham (kwiecień 2006), „Computing with Quantum Knots”, Scientific American , 294 (4): 56–63, Bibcode : 2006SciAm.294d..56C , doi : 10.1038/scientificamerican0406-56 , PMID 16596880
•   Dehn, Max (1914), "Die beiden Kleeblattschlingen", Mathematische Annalen , 75 (3): 402–413, doi : 10.1007/BF01563732 , S2CID 120452571
•   Conway, John H. (1970), „Wyliczenie węzłów i połączeń oraz niektóre z ich właściwości algebraicznych”, Computational Problems in Abstract Algebra , Pergamon, s. 329–358, doi : 10.1016 / B978-0-08-012975 -4.50034-5 , ISBN 978-0-08-012975-4
• Lalka, Helmut; Hoste, Jim (1991), „Tabela zorientowanych linków. Z dodatkiem mikrofiszy”, Math. Komp. , 57 (196): 747–761, Bibcode : 1991MaCom..57..747D , doi : 10.1090/S0025-5718-1991-1094946-4
•   Flapan, Erica (2000), Gdy topologia spotyka się z chemią: topologiczne spojrzenie na chiralność molekularną , Outlook, Cambridge University Press , ISBN 978-0-521-66254-3
•   Haefliger, André (1962), „Wiązane (4 k - 1) -kulki w przestrzeni 6 k ”, Annals of Mathematics , druga seria, 75 (3): 452–466, doi : 10,2307/1970208 , JSTOR 1970208
•   Hass, Joel (1998), „Algorytmy rozpoznawania węzłów i 3-rozmaitości” , Chaos, solitony i fraktale , 9 (4–5): 569–581, arXiv : math / 9712269 , Bibcode : 1998CSF ..... 9 ..569H , doi : 10.1016/S0960-0779(97)00109-4 , S2CID 7381505
•   Gospodarz, Jim; Thistlethwaite, Morwena ; Weeks, Jeffrey (1998), „Pierwsze 1 701 935 węzłów”, Math. Inteligencja , 20 (4): 33–48, doi : 10.1007/BF03025227 , S2CID 18027155
• Hoste, Jim (2005), „Wyliczanie i klasyfikacja węzłów i ogniw” , Handbook of Knot Theory (PDF) , Amsterdam: Elsevier
•   Levine, Jerome (1965), „Klasyfikacja węzłów różniczkowalnych” , Annals of Mathematics , druga seria, 1982 (1): 15–50, doi : 10,2307/1970561 , JSTOR 1970561
•   Kontsevich, Maxim (1993), „Niezmienniki węzłów Wasiliewa”, IM Gelfand Seminar, Adv. radziecka matematyka. , 2, Providence, RI: American Mathematical Society, 16 : 137–150, doi : 10.1090/advsov/016.2/04 , ISBN 9780821841174
•    Lickorish, WB Raymond (1997), Wprowadzenie do teorii węzłów , Graduate Texts in Mathematics, tom. 175, Springer-Verlag, doi : 10.1007/978-1-4612-0691-0 , ISBN 978-0-387-98254-0 , S2CID 122824389
•   Perko, Kenneth (1974), „O klasyfikacji węzłów”, Proceedings of the American Mathematical Society , 45 (2): 262–6, doi : 10,2307/2040074 , JSTOR 2040074
•    Rolfsen, Dale (1976), Węzły i linki , Seria wykładów z matematyki, tom. 7, Berkeley, Kalifornia : Publikuj albo zgiń, ISBN 978-0-914098-16-4 , MR 0515288
• Schubert, Horst (1949), „Die eindeutige Zerlegbarkeit eines Knotens in Primknoten”, Heidelberger Akad. Wiss. Matematyka-Nat. kl. (3): 57–104
• Silver, Dan (2006), „Dziwne początki teorii węzłów” (PDF) , American Scientist , tom. 94, nr. 2, s. 158–165, doi : 10.1511/2006.2.158
• Simon, Jonathan (1986), „Topologiczna chiralność pewnych cząsteczek”, Topology , 25 (2): 229–235, doi : 10.1016/0040-9383 (86) 90041-8
•   Sossinsky, Alexei (2002), Węzły, matematyka z niespodzianką , Harvard University Press, ISBN 978-0-674-00944-8
•   Turaev, Vladimir G. (1994), „Niezmienniki kwantowe węzłów i 3-rozmaitości” , De Gruyter Studies in Mathematics , Berlin: Walter de Gruyter & Co., 18 , arXiv : hep-th/9409028 , Bibcode : 1994hep.th ....9028T , ISBN 978-3-11-013704-0
• Weisstein, Eric W. (2013). „Schemat zredukowanych węzłów” . MathWorld . Wolframa . Źródło 8 maja 2013 r .
• Weisstein, Eric W. (2013a). „Redukowalne przejście” . MathWorld . Wolframa . Źródło 8 maja 2013 r .
•   Witten, Edward (1989), „Kwantowa teoria pola i wielomian Jonesa” , Comm. Matematyka fizyka , 121 (3): 351–399, Bibcode : 1989CMaPh.121..351W , doi : 10.1007/BF01217730 , S2CID 14951363
•   Zeeman, Erik C. (1963), „Rozplątywanie piłek kombinatorycznych”, Annals of Mathematics , druga seria, 78 (3): 501–526, doi : 10.2307/1970538 , JSTOR 1970538

Dalsza lektura

Podręczniki wprowadzające

Istnieje wiele wstępów do teorii węzłów. Klasycznym wprowadzeniem dla doktorantów lub zaawansowanych studentów jest ( Rolfsen 1976 ). Inne dobre teksty z bibliografii to ( Adams 2004 ) i ( Lickorish 1997 ). Adams jest nieformalny i dostępny w większości dla uczniów szkół średnich. Lickorish to rygorystyczne wprowadzenie dla absolwentów, obejmujące przyjemną mieszankę klasycznych i nowoczesnych tematów. ( Cromwell 2004 ) jest odpowiedni dla studentów, którzy znają topologię punktów; nie jest wymagana znajomość topologii algebraicznej.

•   Burde, Gerhard; Zieschang, Heiner (1985), Knots , De Gruyter Studies in Mathematics, tom. 5, Walter de Gruyter, ISBN 978-3-11-008675-1
•   Crowell, Richard H.; Lis, Ralph (1977). Wprowadzenie do teorii węzłów . ISBN 978-0-387-90272-2 .
•   Kauffman, Louis H. (1987), na węzłach , ISBN 978-0-691-08435-0
•   Kauffman, Louis H. (2013), Węzły i fizyka (wyd. 4), World Scientific, ISBN 978-981-4383-00-4
•   Cromwell, Peter R. (2004), Węzły i linki , Cambridge University Press, ISBN 978-0-521-54831-1

Ankiety

•   Menasco, William W.; Thistlethwaite, Morwen , wyd. (2005), Handbook of Knot Theory , Elsevier, ISBN 978-0-444-51452-3
  • Podręcznik Menasco i Thistlethwaite zawiera przegląd różnych tematów związanych z aktualnymi trendami badawczymi w sposób dostępny dla zaawansowanych studentów, ale interesujący dla profesjonalnych badaczy.
•   Livio, Mario (2009), „Rozdział 8: Nieuzasadniona skuteczność?” , Czy Bóg jest matematykiem? , Simon & Schuster, s. 203–218, ISBN 978-0-7432-9405-8

Linki zewnętrzne

• „Matematyka i węzły” To jest internetowa wersja wystawy przygotowanej dla Towarzystwa Królewskiego „PopMath RoadShow” w 1989 roku. Jego celem było wykorzystanie węzłów do zaprezentowania szerokiej publiczności metod matematycznych.

Historia

• Thomson, Sir William (1867), „O atomach wirowych” , Proceedings of the Royal Society of Edinburgh , VI : 94–105
•    Silliman, Robert H. (grudzień 1963), "William Thomson: Smoke Rings and XIX-Century Atomism", Isis , 54 (4): 461–474, doi : 10.1086/349764 , JSTOR 228151 , S2CID 144988108
• Film przedstawiający współczesne odtworzenie eksperymentu Taita z kółkiem dymnym
• Historia teorii węzłów (na stronie domowej Andrzeja Ranickiego )

Tabele węzłów i oprogramowanie

• KnotInfo : Tabela niezmienników węzłów i zasoby teorii węzłów
• The Knot Atlas — szczegółowe informacje o poszczególnych węzłach w tabelach węzłów
• KnotPlot — oprogramowanie do badania właściwości geometrycznych węzłów
• Knotscape — oprogramowanie do tworzenia obrazów węzłów
• Knoutilus — internetowa baza danych i generator obrazów węzłów
• KnotData.html — funkcja Wolfram Mathematica do badania węzłów
• Regina — oprogramowanie do topologii niskowymiarowej z natywną obsługą węzłów i połączeń. Tabele głównych węzłów z maksymalnie 19 skrzyżowaniami