Ruch Reidemeistera

ruchy Reidemeistera

typ I	Typ II	Typ III

Zmodyfikowany ruch Reidemeistera

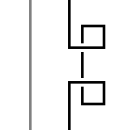
Typ I'

W matematycznym obszarze teorii węzłów ruch Reidemeistera to jeden z trzech ruchów lokalnych na diagramie połączeń . Kurt Reidemeister ( 1927 ) i niezależnie James Waddell Alexander i Garland Baird Briggs ( 1926 ) wykazali, że dwa diagramy węzłów należące do tego samego węzła, aż do płaskiej izotopii , mogą być powiązane sekwencją trzech ruchów Reidemeistera.

Każdy ruch działa na małym obszarze diagramu i jest jednym z trzech typów:

1. Skręć i odkręć w dowolnym kierunku.
2. Przesuń całkowicie jedną pętlę nad drugą.
3. Przesuń strunę całkowicie nad lub pod skrzyżowaniem.

Żadna inna część diagramu nie jest zaangażowana w obraz ruchu, a planarna izotopia może zniekształcić obraz. Numeracja rodzajów ruchów odpowiada liczbie zaangażowanych wątków, np. ruch typu II działa na dwóch pasmach diagramu.

Jednym z ważnych kontekstów, w których pojawiają się ruchy Reidemeistera, jest definiowanie niezmienników węzłów . Demonstrując właściwość diagramu węzłów, która nie zmienia się, gdy zastosujemy którykolwiek z ruchów Reidemeistera, definiujemy niezmiennik. W ten sposób można zdefiniować wiele ważnych niezmienników, w tym wielomian Jonesa .

Typ ruchu, którym się poruszam, jest jedynym ruchem, który wpływa na skręcanie diagramu. Ruch typu III jako jedyny nie zmienia numeru skrzyżowania diagramu.

W zastosowaniach takich jak rachunek Kirby'ego , w których pożądaną klasą równoważności diagramów węzłów nie jest węzeł, ale ramkowe połączenie , należy zastąpić ruch typu I ruchem „zmodyfikowanego typu I” (typ I') złożonym z dwóch typów I porusza się w przeciwnym kierunku. Ruch typu I nie wpływa ani na kadrowanie ogniwa, ani na skręcenie całego schematu węzła.

Trace (1983) wykazał, że dwa diagramy węzłów dla tego samego węzła są powiązane przy użyciu tylko ruchów typu II i III wtedy i tylko wtedy, gdy mają tę samą liczbę skrętów i zwojów . Ponadto połączone prace Östlund (2001) , Manturova (2004) i Hagge (2006) pokazuje, że dla każdego typu węzła istnieje para diagramów węzłów, tak że każda sekwencja ruchów Reidemeistera przechodzących jeden w drugi musi wykorzystywać wszystkie trzy rodzaje ruchów. Alexander Coward wykazał, że dla diagramów połączeń reprezentujących równoważne powiązania istnieje sekwencja ruchów uporządkowanych według typu: najpierw ruchy typu I, następnie ruchy typu II, typu III, a następnie typu II. Ruchy poprzedzające ruchy typu III zwiększają liczbę skrzyżowań, a te po nich zmniejszają liczbę skrzyżowań.

Coward i Lackenby (2014) udowodnili istnienie wykładniczej górnej granicy wieży (w zależności od liczby skrzyżowań) liczby ruchów Reidemeistera wymaganych do przejścia między dwoma diagramami tego samego łącza. W szczegółach niech $sumą$ przecinających się liczb z dwóch diagramów, wtedy górna granica to $\ Displaystyle 2 ^ {2 ^ {2 ^ {. ^ {. ^ {n}}}}}} gdzie$$displaystyle$ wysokość wieży s (z pojedynczym $n}$${\ Displaystyle 10 ^ {1 000 000 n}$ góry) jest

Lackenby (2015) udowodnił istnienie górnego ograniczenia wielomianu (w zależności od liczby skrzyżowań) liczby ruchów Reidemeistera wymaganych do zmiany diagramu węzła na standardowy węzeł. Szczegółowo, dla każdego takiego diagramu ze $skrzyżowaniami$ górna granica to ${\ Displaystyle (236c) ^ {11}$ .

Hayashi (2005) udowodnił, że istnieje również górna granica, zależna od liczby skrzyżowań, od liczby ruchów Reidemeistera wymaganych do podzielenia łącza .

• Media związane z ruchami Reidemeistera w Wikimedia Commons
•    Aleksander, James W.; Briggs, Garland B. (1926), „O typach krzywych wiązanych”, Annals of Mathematics , 28 (1/4): 562–586, doi : 10.2307/1968399 , JSTOR 1968399 , MR 1502807
•    Tchórz, Aleksander; Lackenby, Marc (2014), „Górna granica ruchów Reidemeistera” , American Journal of Mathematics , 136 (4): 1023–1066, arXiv : 1104,1882 , doi : 10,1353/ajm.2014.0027 , MR 3245186 , S2CID 55882290
•   Galatolo, Stefano (1999), „O problemie w efektywnej teorii węzłów” , Atti Accad. Naz. Lincei kl. nauka fis. Mata. Natura. Rozdzierać. Lincei (9) Mat. Aplikacja , 9 (4): 299–306, MR 1722788
•   Hagge, Tobias (2006), „Każdy ruch Reidemeistera jest potrzebny dla każdego rodzaju węzła”, Proc. Amer. Matematyka soc. , 134 (1): 295–301, doi : 10.1090/S0002-9939-05-07935-9 , MR 2170571
•    Hass, Joel ; Lagarias, Jeffrey C. (2001), „Liczba ruchów Reidemeistera potrzebnych do odwiązania” , Journal of the American Mathematical Society , 14 (2): 399–428, arXiv : math / 9807012 , doi : 10.1090 / S0894-0347- 01-00358-7 , MR 1815217 , S2CID 15654705
•    Hayashi, Chuichiro (2005), „Liczba ruchów Reidemeistera do podziału łącza”, Mathematische Annalen , 332 (2): 239–252, doi : 10,1007 / s00208-004-0599-x , MR 2178061 , S2CID 119728321
•    Lackenby, Marc (2015), „Górna granica wielomianu ruchów Reidemeistera”, Annals of Mathematics , Second Series, 182 (2): 491–564, arXiv : 1302,0180 , doi : 10,4007/annals.2015.182.2.3 , MR 3418524 , S2CID 119662237
•    Manturov, Vassily Olegovich (2004), teoria węzłów , Boca Raton, FL: Chapman & Hall / CRC, doi : 10.1201/9780203402849 , ISBN 0-415-31001-6 , MR 2068425
•    Östlund, Olof-Petter (2001), „Niezmienności diagramów i relacji między ruchami Reidemeister”, J. Knot Theory Teory Conseat , 10 (8): 1215–1227, Arxiv : Math/0005108 , doi : 10.1142/s0218216501001402 , MR 187126. , S2CID 119177881
•    Reidemeister, Kurt (1927), "Elementare Begründung der Knotentheorie", Abh. Matematyka Sem. Uniw. Hamburg , 5 (1): 24–32, doi : 10.1007/BF02952507 , MR 3069462 , S2CID 120149796
•    Trace, Bruce (1983), „O ruchach Reidemeistera klasycznego węzła”, Proceedings of the American Mathematical Society , 89 (4): 722–724, doi : 10.2307/2044613 , JSTOR 2044613 , MR 0719004