monodromia

Część urojona logarytmu zespolonego . Próba zdefiniowania logarytmu zespolonego na C \ {0} daje różne odpowiedzi wzdłuż różnych ścieżek. Prowadzi to do nieskończonej cyklicznej grupy monodromicznej i pokrycia C \ {0} przez helikoidę (przykład powierzchni Riemanna ).

W matematyce monodromia to nauka o tym, jak obiekty z analizy matematycznej , topologii algebraicznej , geometrii algebraicznej i geometrii różniczkowej zachowują się, gdy „obiegają” osobliwość . Jak sama nazwa wskazuje, podstawowe znaczenie monodromii pochodzi od „biegania pojedynczo”. Jest to ściśle związane z zakrywaniem map i ich degeneracją w rozgałęzienia ; aspektem powodującym zjawisko monodromii jest to, że pewne funkcje, które moglibyśmy chcieć zdefiniować, nie są jednowartościowe , gdy „biegamy” po ścieżce otaczającej osobliwość. Niepowodzenie monodromii można zmierzyć, definiując grupę monodromii : grupę transformacji działających na danych, które kodują to, co dzieje się, gdy „biegniemy” w jednym wymiarze. Brak monodromii jest czasami nazywany polidromią .

Definicja

Niech X będzie połączoną i lokalnie połączoną bazową przestrzenią topologiczną z punktem bazowym x i niech będzie pokryciem z włóknem ${\ Displaystyle F = p ^ {- 1} (x)}$${\ Displaystyle p: {\ tylda {X}} \ do X}$ . Dla pętli γ: [0, 1] → X opartej na x , oznacz windę $\ Displaystyle$ punktu , przez $}}$ . Na koniec oznaczamy przez $1)}$ końcowy $gamma$${\ Displaystyle {\ tylda {$ , co generalnie różni się od ${\ Displaystyle {\ tylda {x}}}$ . Istnieją twierdzenia, które stwierdzają, że ta konstrukcja daje dobrze zdefiniowane działanie grupowe grupy podstawowej π ₁ ( X , x ) na F , a stabilizatorem jest dokładnie ${\ Displaystyle p_ {*} \ lewo (\ pi _ {1} \ lewo ({\ tylda {X}}, {\ tylda {x}} \ prawej) \ Prawidłowy)}$${\ Displaystyle {\ tylda {x}}}$ , to znaczy element [γ] ustala punkt w F wtedy i tylko wtedy, gdy jest reprezentowany przez obraz pętli w ${\ Displaystyle {\ tylda {X}}}$ na podstawie ${\ displaystyle {\ tylda {x}}}$ . To działanie nazywa się działaniem monodromicznym i odpowiadający mu homomorfizm π ₁ ( X , x ) → Aut( H _* ( F _x )) do grupy automorfizmów na F jest monodromią algebraiczną . Obrazem tego homomorfizmu jest grupa monodromiczna . Istnieje inne odwzorowanie π ₁ ( X , x ) → Diff( F _x )/Is( F _x ) którego obraz nazywamy topologiczną grupą monodromiczną .

Przykład

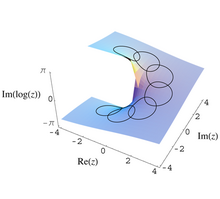
Idee te zostały po raz pierwszy wyrażone w złożonej analizie . W procesie kontynuacji analitycznej funkcja, która jest funkcją analityczną F ( z ) w pewnym otwartym podzbiorze E przebitej płaszczyzny zespolonej ℂ \ {0} , może być kontynuowana z powrotem do E , ale z innymi wartościami. Na przykład weź

${\ Displaystyle {\ rozpocząć {wyrównane} F (z) & = \ log (z) \\ E & = \ { z\in \mathbb {C} \mid \operatorname {Re} (z)>0\}\end{wyrównane}}}$

następnie analityczna kontynuacja w kierunku przeciwnym do ruchu wskazówek zegara wokół koła

${\ displaystyle | z| = 1}$

spowoduje powrót, nie do F ( z ), ale

${\ Displaystyle F (z) + 2 \ pi ja}$

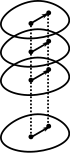
W tym przypadku grupa monodromii jest nieskończenie cykliczna , a przestrzeń pokrycia jest uniwersalnym pokryciem przebitej płaszczyzny zespolonej. Tę osłonę można zwizualizować jako helikoidę (zgodnie z definicją w artykule o helikoidzie) ograniczoną do ρ > 0 . Mapa nakrywająca jest rzutem pionowym, w pewnym sensie załamującym spiralę w oczywisty sposób, aby uzyskać przebitą płaszczyznę.

Równania różniczkowe w dziedzinie zespolonej

Jednym z ważnych zastosowań są równania różniczkowe , w których pojedyncze rozwiązanie może dać dalsze liniowo niezależne rozwiązania poprzez kontynuację analityczną . Liniowe równania różniczkowe zdefiniowane w otwartym, spójnym zbiorze S na płaszczyźnie zespolonej mają grupę monodromiczną, która (dokładniej) jest liniową reprezentacją podstawowej grupy S , podsumowującą wszystkie analityczne kontynuacje okrągłych pętli w S . Odwrotny problem konstrukcji równania (z regularnymi osobliwościami ), biorąc pod uwagę reprezentację, nazywa się problemem Riemanna – Hilberta .

Dla regularnego (w szczególności fuchsowskiego) układu liniowego jako generatory grupy monodromii wybiera się zwykle operatory Mj _. odpowiadające pętlom, z których każdy omija tylko jeden z biegunów układu w kierunku przeciwnym do ruchu wskazówek zegara Jeśli indeksy j są dobrane w taki sposób, że rosną od 1 do p + 1, gdy omija się punkt bazowy zgodnie z ruchem wskazówek zegara, to jedyną relacją między generatorami jest równość ${\ Displaystyle M_ {1} \ cdots M_ {p + 1} = \ operatorname {identyfikator}}$ . Problem Deligne’a-Simpsona jest następującym problemem realizacyjnym: Dla jakich krotek klas koniugacji w GL( n , C ) istnieją nieredukowalne krotki macierzy M _j z tych klas spełniające powyższą zależność? Problem został sformułowany przez Pierre'a Deligne'a i Carlosa Simpsona jako pierwszy uzyskał wyniki w kierunku jego rozwiązania. Addytywna wersja problemu dotyczącego pozostałości systemów Fuchsa została sformułowana i zbadana przez Vladimira Kostova. Problem ten był rozważany przez innych autorów również dla grup macierzowych innych niż GL( n , C ).

Aspekty topologiczne i geometryczne

W przypadku mapy pokrywającej patrzymy na to jako na szczególny przypadek fibracji i używamy właściwości podnoszenia homotopii , aby „podążać” ścieżkami w przestrzeni bazowej X ( dla uproszczenia zakładamy, że jest to połączone ścieżkami ), gdy są one podnoszone do pokrywy C . Jeśli wykonamy pętlę opartą na x w X , którą podniesiemy, aby rozpocząć w punkcie c powyżej x , zakończymy ponownie w pewnym c* powyżej x ; całkiem możliwe, że C ≠ c* , a aby to zakodować, rozważa się działanie grupy podstawowej π ₁ ( X , x ) jako grupy permutacyjnej na zbiorze wszystkich c , w tym kontekście jako grupy monodromicznej .

W geometrii różniczkowej analogiczną rolę pełni transport równoległy . W wiązce głównej B nad gładkim kolektorem M połączenie umożliwia „ poziomy ” ruch włókien powyżej m w M do sąsiednich. Efekt zastosowany do pętli opartych na m polega na zdefiniowaniu grupy holonomii translacji włókna w m ; jeśli grupą strukturalną B jest G , jest to podgrupa G który mierzy odchylenie B od pakietu produktów M × G .

Grupoidy monodromiczne i foliacje

Ścieżka w podstawie ma ścieżki w całej przestrzeni, które ją podnoszą. Pchanie wzdłuż tych ścieżek daje działanie monodromiczne z podstawowego groupoidu.

Analogicznie do grupoidy podstawowej można zrezygnować z wyboru punktu bazowego i zdefiniować grupoidę monodromiczną. Rozważamy tutaj (klasy homotopii) wyciągów ścieżek w przestrzeni podstawowej X rozwłóknienia ${\ Displaystyle p: {\ tylda {X}} \ do X}$ . Wynik ma strukturę groupoidy nad przestrzenią bazową X . Zaletą jest to, że możemy odrzucić warunek łączności X .

$Rozważ$ więcej, konstrukcję można również uogólnić na foliowanie : pojedynczą foliację M Następnie dla każdej ścieżki w liściu $.$ rozważyć jej indukowany dyfeomorfizm na lokalnych przekrojach poprzecznych przez punkty końcowe W prostym połączonym wykresie ten dyfeomorfizm staje się wyjątkowy, a zwłaszcza kanoniczny między różnymi przekrojami poprzecznymi, jeśli przejdziemy do zarodka dyfeomorfizmu wokół punktów końcowych. W ten sposób staje się również niezależny od ścieżki (między ustalonymi punktami końcowymi) w prosto połączonym wykresie, a zatem jest niezmienny w warunkach homotopii.

Definicja za pomocą teorii Galois

Niech F ( x ) oznacza ciało funkcji wymiernych w zmiennej x nad ciałem F , które jest ciałem ułamków pierścienia wielomianu F [ x ]. Element y = f ( x ) z F ( x ) określa skończone rozszerzenie pola [ F ( x ) : F ( y )].

To rozszerzenie generalnie nie jest Galois, ale ma zamknięcie Galois L ( f ). Powiązana grupa Galois rozszerzenia [ L ( f ) : F ( y )] nazywana jest grupą monodromiczną f .

W przypadku F = C teoria powierzchni Riemanna wchodzi i pozwala na interpretację geometryczną podaną powyżej. W przypadku, gdy rozszerzenie [ C ( x ) : C ( y )] jest już Galois, powiązana grupa monodromii jest czasami nazywana grupą transformacji talii .

Ma to związek z teorią pokrywania przestrzeni Galois, prowadzącą do twierdzenia o istnieniu Riemanna .

Zobacz też

• Grupa warkoczy
• Twierdzenie o monodromii
• Grupa klas mapowania (przebitego dysku)

Notatki

• VI Danilov (2001) [1994], „Monodromia” , Encyklopedia matematyki , EMS Press
• „Group-groupoids i monodromy groupoids”, O. Mucuk, B. Kılıçarslan, T. ¸Sahan, N. Alemdar, Topology and its Applications 158 (2011) 2034–2042 doi : 10.1016 / j.topol.2011.06.048
• R. Brown Topologia i grupoidy (2006).
• PJ Higgins, „Kategorie i grupoidy”, van Nostrand (1971) TAC Przedruk
• H. Żołądek, "Grupa Monodromy", Birkhäuser Basel 2006; doi: 10.1007/3-7643-7536-1