Octacube (rzeźba)
Octacube to duża rzeźba ze stali nierdzewnej wystawiona na wydziale matematyki Uniwersytetu Stanowego Pensylwanii w State College w Pensylwanii . Rzeźba przedstawia obiekt matematyczny zwany 24-komorową lub „ośmiosześcianem”. Ponieważ prawdziwy 24-komorowy jest czterowymiarowy , grafika jest w rzeczywistości projekcją do trójwymiarowego świata.
Octacube ma bardzo wysoką wewnętrzną symetrię , która pasuje do cech chemii ( symetria molekularna ) i fizyki ( kwantowa teoria pola ).
Rzeźba została zaprojektowana przez Adriana Ocneanu, profesora matematyki na Pennsylvania State University . Uniwersytecki warsztat maszynowy spędził ponad rok na wykonywaniu skomplikowanych prac metalowych. Octacube został ufundowany przez absolwentkę ku pamięci jej męża, Kermita Andersona, który zginął w atakach z 11 września .
Grafika
Metalowy szkielet Octacube mierzy około 1,8 metra we wszystkich trzech wymiarach. Jest to złożony układ niepomalowanych, trójkątnych kołnierzy. Podstawą jest granitowy blok o wysokości 3 stóp (0,91 metra) z pewnymi grawerunkami.
Grafika została zaprojektowana przez Adriana Ocneanu, profesora matematyki z Penn State. Dostarczył specyfikacje dla 96 trójkątnych elementów rzeźby ze stali nierdzewnej i ich montażu. Produkcja została wykonana przez warsztat mechaniczny Penn State, kierowany przez Jerry'ego Andersona. Prace trwały ponad rok, obejmując gięcie i spawanie oraz cięcie. Omawiając budowę, Ocneanu powiedział:
Bardzo trudno jest sprawić, by 12 stalowych arkuszy spotkało się idealnie — i odpowiednio — w każdym z 23 wierzchołków, bez śladu spawania. Ludzie, którzy go zbudowali, to naprawdę światowej klasy eksperci i perfekcjoniści – artyści ze stali.
Ze względu na odblaskowy metal pod różnymi kątami, wygląd jest przyjemnie dziwny. W niektórych przypadkach lustrzane powierzchnie tworzą iluzję przezroczystości, ukazując odbicia z nieoczekiwanych stron konstrukcji. Twórca rzeźby, matematyk, skomentował:
Kiedy zobaczyłem prawdziwą rzeźbę, przeżyłem niezły szok. Nigdy nie wyobrażałem sobie gry światła na powierzchniach. Istnieją subtelne efekty optyczne, które można wyczuć, ale nie można ich dokładnie określić.
- Widoki Octacube pod różnymi kątami
Interpretacja
Regularne kształty
Bryły platońskie to trójwymiarowe kształty o szczególnej, wysokiej symetrii . Są kolejnym krokiem w wymiarze w porównaniu z dwuwymiarowymi wielokątami foremnymi (kwadraty, trójkąty równoboczne itp.). Pięć brył platońskich to czworościan (4 ściany), sześcian (6 ścian), ośmiościan (8 ścian), dwunastościan (12 ścian) i dwudziestościan (20 twarzy). Znane były już od czasów starożytnych Greków i cenione ze względu na ich walory estetyczne i filozoficzne, a nawet mistyczne znaczenie. (Zobacz także Timajos , dialog Platona ).
| Bryły platońskie | ||||

|

|

|

|

|
| Czworościan | Sześcian | Oktaedr | Dwunastościan | dwudziestościan |
W wyższych wymiarach odpowiednikami brył platońskich są regularne polytopy . Kształty te zostały po raz pierwszy opisane w połowie XIX wieku przez szwajcarskiego matematyka Ludwiga Schläfliego . W czterech wymiarach jest ich sześć : pentachoron ( 5-komorowy ), tesserakt ( 8-komorowy ), heksadekachoron ( 16-komorowy ), oktasześcian ( 24-komorowy ), hecatonicosachoron ( 120-komorowy ) i heksacosichoron ( 600-ogniwowy ).
24 komórki składają się z 24 ośmiościanów połączonych w 4-wymiarowej przestrzeni. Figura wierzchołka 24 komórek (trójwymiarowy kształt utworzony po odcięciu narożnika 4-D) jest sześcianem. Pomimo swojej sugestywnej nazwy, ośmiościan nie jest czterowymiarowym analogiem ani ośmiościanu, ani sześcianu. W rzeczywistości jest to jedyny z sześciu regularnych polytopów 4-D, któremu brakuje odpowiedniej bryły platońskiej.
| Próby zobrazowania 24-ogniwowego | ||
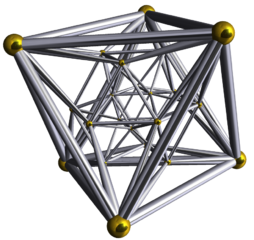
|

|
|
| diagram Schlegla | Obrót w 4 wymiarach | |
projekcje

Ocneanu wyjaśnia koncepcyjne wyzwanie związane z pracą w czwartym wymiarze: „Chociaż matematycy mogą abstrakcyjnie pracować z czwartym wymiarem, dodając czwartą współrzędną do trzech, których używamy do opisania punktu w przestrzeni, czwarty wymiar przestrzenny jest trudny do wizualizacji”.
Chociaż niemożliwe jest zobaczenie lub wykonanie obiektów 4-wymiarowych, możliwe jest odwzorowanie ich w niższych wymiarach, aby uzyskać ich wrażenie. Analogią do przekształcenia 4-D 24-komórkowej w jej trójwymiarową rzeźbę jest rzut kartograficzny , w którym powierzchnia trójwymiarowej Ziemi (lub kuli ziemskiej) jest zredukowana do płaskiej płaszczyzny dwuwymiarowej (przenośna mapa). Odbywa się to albo za pomocą światła „rzucającego cień” z globu na mapę, albo za pomocą matematycznej transformacji. Istnieje wiele różnych rodzajów odwzorowań map: znany prostokątny Mercator (używany do nawigacji), okrągły gnomon (pierwsza wynaleziona projekcja) i kilka innych. Wszystkie mają swoje ograniczenia, ponieważ przedstawiają niektóre cechy w zniekształcony sposób – „nie można spłaszczyć skórki pomarańczy bez jej uszkodzenia” – ale są użyteczną pomocą wizualną i wygodnymi odniesieniami.
W ten sam sposób, w jaki zewnętrzna część Ziemi jest powłoką 2D (wygiętą do trzeciego wymiaru), zewnętrzna część 4-wymiarowego kształtu jest przestrzenią 3D (ale złożoną przez hiperprzestrzeń, czwarty wymiar). Jednakże, podobnie jak powierzchnia kuli ziemskiej nie może być zmapowana na płaszczyźnie bez pewnych zniekształceń, tak samo nie można odwzorować zewnętrznego kształtu 3D 24-komorowego hiper-kształtu 4-D. Na obrazie po prawej 24 komórki są wyświetlane w przestrzeni jako obiekt trójwymiarowy (a następnie obraz jest jego dwuwymiarowym renderowaniem, z perspektywą ułatwiającą oko ) . Niektóre z przekłamań:
- Zakrzywione linie krawędzi: są proste w czterech wymiarach, ale rzutowanie na niższy wymiar sprawia, że wydają się zakrzywione (podobne efekty występują podczas mapowania Ziemi).
- Konieczne jest użycie półprzezroczystych powierzchni ze względu na złożoność obiektu, dzięki czemu widać wiele „pudełek” (ośmiościennych komórek).
- Wyraźnie widać tylko 23 komórki. 24. komórka to „zewnętrzne wnętrze”, cała zewnętrzna przestrzeń wokół obiektu widziana w trzech wymiarach.
Aby zmapować 24 komórki, Ocneanu używa pokrewnej projekcji, którą nazywa promieniową projekcją stereograficzną w oknie . Podobnie jak w przypadku projekcji stereograficznej, w przestrzeni trójwymiarowej pokazane są zakrzywione linie. Zamiast stosowania półprzezroczystych powierzchni, w powierzchniach komórek wycina się „okna”, aby można było zobaczyć komórki wewnętrzne. Ponadto fizycznie obecne są tylko 23 wierzchołki. 24. wierzchołek „występuje w nieskończoności” z powodu rzutu; widać 8 nóg i ramion rzeźby rozchodzących się na zewnątrz od środka trójwymiarowej rzeźby.
Symetria

Rzeźba Octacube ma bardzo wysoką symetrię. Konstrukcja ze stali nierdzewnej ma taką samą symetrię jak sześcian lub ośmiościan. Dzieło sztuki można zwizualizować jako odnoszące się do sześcianu: ramiona i nogi konstrukcji rozciągają się do rogów. Wyobrażenie sobie ośmiościanu jest trudniejsze; polega na myśleniu o ścianach wizualizowanego sześcianu tworzących rogi ośmiościanu. Sześcian i ośmiościan mają tę samą wielkość i typ symetrii: symetrię ośmiościenną , zwaną w notacji matematycznej O h (rząd 48). Niektóre, ale nie wszystkie, elementy symetrii są
- 3 różne czterokrotne osie obrotu (po jednej przez każdą parę przeciwległych ścian wizualizowanego sześcianu): góra/dół, do wewnątrz/na zewnątrz i lewo/prawo, jak widać na fotografii
- 4 różne potrójne osie obrotu (jedna przechodząca przez każdą parę przeciwległych rogów sześcianu [wzdłuż każdej z przeciwstawnych par rąk/nog])
- 6 różnych podwójnych osi obrotu (jedna przechodząca przez środek każdej przeciwległej krawędzi wizualizowanego sześcianu)
- 9 lustrzanych płaszczyzn, które przecinają wizualizowany sześcian
- 3, które przycinają górę/dół, lewo/prawo i przód/tył. Te lustra reprezentują jego odbijającą subsymetrię dwuścienną D 2h , rząd 8 (symetria podrzędna dowolnego obiektu o symetrii oktaedrycznej)
- 6, które idą wzdłuż przekątnych przeciwległych ścian wizualizowanego sześcianu (idą one wzdłuż podwójnych zestawów par ręka-noga). Te zwierciadła reprezentują jego odblaskową subsymetrię czworościenną T d , rząd 24 (symetria podrzędna dowolnego obiektu o symetrii oktaedrycznej).
Wykorzystując punkty środkowego pomieszczenia, rzeźba przedstawia systemy korzeniowe typu D4, B4=C4 i F4, czyli wszystkie 4d inne niż A4. Może wizualizować projekcję D4 do B3 i D4 do G2.
Aluzje naukowe
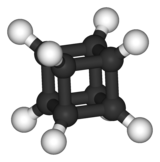
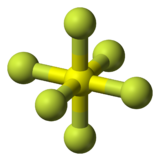
Wiele cząsteczek ma taką samą symetrię jak rzeźba Octacube . Jednym z przykładów jest cząsteczka organiczna, kuban (C 8 H 8 ). Ramiona i nogi rzeźby są podobne do wystających na zewnątrz atomów wodoru. Sześciofluorek siarki (lub dowolna cząsteczka o dokładnej ośmiościennej geometrii cząsteczkowej ) również ma tę samą symetrię, chociaż podobieństwo nie jest tak podobne.
|
|
| kubański | Sześciofluorek siarki |
Octacube pokazuje również podobieństwa do pojęć z fizyki teoretycznej . Twórca Ocneanu bada matematyczne aspekty kwantowej teorii pola (QFT). Temat ten został opisany przez medalu Fieldsa , Eda Wittena , jako najtrudniejszy obszar w fizyce. Częścią pracy Ocneanu jest budowanie teoretycznych, a nawet fizycznych modeli cech symetrii w QFT. Ocneanu cytuje związek wewnętrznej i zewnętrznej połowy struktury jako analogiczny do związku cząstek o spinie 1/2 (np. elektronów ) i cząstki o spinie 1 (np. fotony ).
Memoriał
Octacube został zamówiony i sfinansowany przez Jill Anderson, absolwentkę matematyki PSU z 1965 roku, ku pamięci jej męża, Kermita, innego absolwenta matematyki z 1965 roku, który zginął w atakach terrorystycznych z 11 września . Podsumowując memoriał, Anderson powiedział:
Mam nadzieję, że rzeźba zachęci studentów, wykładowców, administratorów, absolwentów i przyjaciół do refleksji i docenienia wspaniałego świata matematyki. Mam również nadzieję, że wszyscy, którzy oglądają rzeźbę, zaczną dostrzegać otrzeźwiający fakt, że każdy jest narażony na to, że przydarzy mu się coś strasznego, i że wszyscy musimy nauczyć się żyć dzień po dniu, wykorzystując jak najlepiej to, co zostało dane nas. Byłoby wspaniale, gdyby każdy, kto ogląda Octacube, odszedł z poczuciem, że życzliwość dla innych to dobry sposób na życie.
Anderson ufundował również stypendium matematyczne w imieniu Kermita, w tym samym czasie projekt rzeźby posuwał się naprzód.
Przyjęcie
Pełniejsze wyjaśnienie rzeźby, w tym sposób jej powstania, sposób finansowania jej budowy oraz jej rolę w matematyce i fizyce , zostało udostępnione przez Penn State. Ponadto Ocneanu przedstawił swój własny komentarz.
Zobacz też
Artyści:
- Salvador Dalí , malarz aluzji do czwartego wymiaru
- David Smith , rzeźbiarz abstrakcyjnej, geometrycznej stali nierdzewnej
- Tony Smith , inny twórca dużych abstrakcyjnych rzeźb geometrycznych
Matematyka:
- Teoria grup , dyscyplina matematyczna, która historycznie obejmowała wiele badań nad symetrią
- Algebra operatorów i teoria reprezentacji , obszary badań matematycznych Ocneanu
Notatki
Cytaty
Linki zewnętrzne
- Film z Penn State o Octacube
- Użytkownik stworzył film przedstawiający wyobrażanie sobie czterowymiarowego obiektu (ale tesseraktu). Zwróć uwagę na omówienie prognoz po ~22 minutach i omówienie komórek w modelu po ~35 minutach.





