Teodor z Cyreny

Ten artykuł dotyczy Teodora, matematyka z Cyreny. Dla ateisty również z Cyreny, patrz Teodor ateista .

Teodor z Cyreny ( grecki : Θεόδωρος ὁ Κυρηναῖος ) był starożytnym greckim matematykiem żyjącym w V wieku pne. Jedyne relacje z pierwszej ręki o nim, które przetrwały, znajdują się w trzech dialogach Platona: Teajtecie , Sofiście i Mężu stanu . W poprzednim dialogu stawia twierdzenie matematyczne znane obecnie jako Spirala Teodora .

Życie

Niewiele wiadomo o biografii Teodora poza tym, co można wywnioskować z dialogów Platona. Urodził się w północnoafrykańskiej kolonii Cyreny i najwyraźniej nauczał zarówno tam, jak iw Atenach. Narzeka na starość w Theaetetus , którego dramatyczna data 399 pne sugeruje, że jego okres rozkwitu przypadł na połowę V wieku. Tekst kojarzy go również z sofistą Protagorasem , z którym, jak twierdzi, studiował przed przejściem do geometrii. Wątpliwa tradycja powtarzana wśród starożytnych biografów, takich jak Diogenes Laertius, utrzymywała, że ​​Platon studiował później u niego w Cyrena , Libia. Według Plutarcha, który sam był kapłanem świątyni w Delfach, ten wybitny matematyk Teodor, wraz z Alcybiadesem i wieloma innymi towarzyszami Sokratesa (z których wielu byłoby związanych z trzydziestoma tyranami), został oskarżony o rozdawanie tajemnic na sympozjum .

Praca w matematyce

Dzieło Teodora jest znane dzięki jedynemu twierdzeniu, które jest dostarczane w kontekście literackim Teajteta i na przemian argumentowano, że jest historycznie dokładne lub fikcyjne. W tekście jego uczeń Teajtet przypisuje mu twierdzenie, że pierwiastki kwadratowe liczb niekwadratowych do 17 są niewymierne:

Tutaj Teodor rysował dla nas kilka figur ilustrujących pierwiastki, pokazując, że kwadraty zawierające trzy stopy kwadratowe i pięć stóp kwadratowych nie są współmierne w długości z jednostką stopy, więc wybierając każdy po kolei aż do kwadratu zawierającego siedemnaście stóp kwadratowych i na tym się zatrzymał.

Kwadrat zawierający dwie jednostki kwadratowe nie jest wymieniony, być może dlatego, że niewspółmierność jego boku z jednostką była już znana.) Metoda dowodu Teodora nie jest znana. Nie wiadomo nawet, czy w cytowanym fragmencie „aż do” (μέχρι) oznacza, że ​​obejmuje siedemnaście. Jeśli wykluczono siedemnaście, dowód Teodora mógł polegać jedynie na rozważeniu, czy liczby są parzyste, czy nieparzyste. Rzeczywiście, Hardy, Wright i Knorr sugerują dowody, które ostatecznie opierają się na następującym twierdzeniu: Jeśli ${\ Displaystyle x ^ {2} = ny ^ {2}}$ jest rozpuszczalny w liczbach całkowitych , a $n$ nieparzysty, to $8$ być przystający do 1 modulo (ponieważ i można założyć, że są nieparzyste, więc $}$$displaystyle n$ ich kwadraty są przystające do 1 modulo 8.

To, że nie można udowodnić irracjonalności pierwiastka kwadratowego z 17 przez rozważania ograniczone do arytmetyki parzystych i nieparzystych, zostało pokazane w jednym systemie arytmetyki parzystych i nieparzystych w i, ale jest to problem otwarty w silniejszym naturalny system aksjomatów dla arytmetyki parzystych i nieparzystych

Możliwość zasugerowana wcześniej przez Zeuthena polega na tym, że Teodor zastosował tak zwany algorytm euklidesowy , sformułowany w Twierdzeniu X.2 Elementów jako test na niewspółmierność. Współcześnie twierdzenie mówi, że liczba rzeczywista z nieskończonym ciągłym rozwinięciem ułamka jest niewymierna. Irracjonalne pierwiastki kwadratowe mają okresowe rozwinięcia . Okres pierwiastka kwadratowego z 19 ma długość 6, która jest większa niż okres pierwiastka kwadratowego z dowolnej mniejszej liczby. Okres √17 ma długość jeden (tak samo jak √18; ale irracjonalność √18 wynika z tego z √ 2).

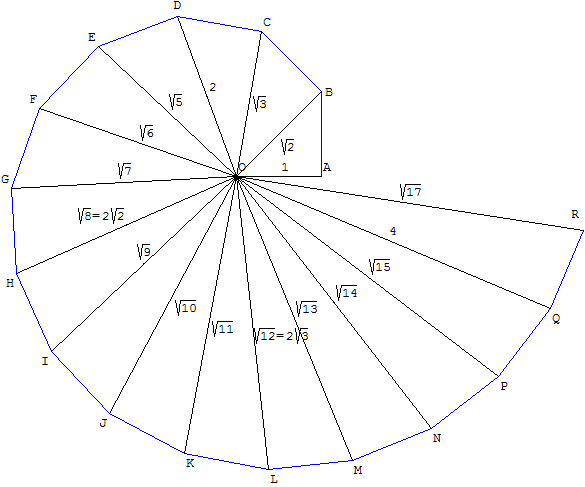
Tak zwana Spirala Teodora składa się z przylegających do siebie trójkątów prostokątnych o przeciwprostokątnych długościach równych √2, √3, √4, …, √17; dodatkowe trójkąty powodują nakładanie się diagramu. Philip J. Davis interpolował wierzchołki spirali, aby uzyskać ciągłą krzywą. Omówił historię prób ustalenia metody Teodora w swojej książce Spirals: From Theodorus to Chaos i czyni krótkie odniesienia do tej sprawy w swojej fikcyjnej serii Thomasa Graya .

Spirala Teodora

To, że Theaetetus ustanowił bardziej ogólną teorię liczb niewymiernych, zgodnie z którą pierwiastki kwadratowe liczb innych niż kwadratowe są niewymierne, sugeruje tytułowy dialog platoński, a także komentarz i scholia do Elementów .

Zobacz też

• Chronologia starożytnych greckich matematyków
• Lista mówców w dialogach Platona
• Kwadratowy irracjonalny
• Wilbura Knorra

Dalsza lektura

• Choike, James R. (1980). „Dowody irracjonalności Teodora”. Dwuletni College Mathematics Journal .
• Gow, James (1884). Krótka historia matematyki greckiej . Uniwersytecki Dom wydawniczy. P. 85 .