algebra geometryczna

Aby zapoznać się z ogólną strukturą algebraiczną, zobacz algebrę Clifforda . W przypadku innych zastosowań zobacz Algebra geometryczna (ujednoznacznienie) .

Nie mylić z geometrią algebraiczną .

W matematyce algebra geometryczna (znana również jako prawdziwa algebra Clifforda ) jest rozszerzeniem algebry elementarnej do pracy z obiektami geometrycznymi, takimi jak wektory . Algebra geometryczna jest zbudowana z dwóch podstawowych operacji, dodawania i iloczynu geometrycznego. Mnożenie wektorów skutkuje obiektami o wyższych wymiarach, zwanymi multiwektorami . W porównaniu z innymi formalizmami do manipulowania obiektami geometrycznymi, algebra geometryczna jest godna uwagi ze względu na wspieranie dzielenia wektorów i dodawania obiektów o różnych wymiarach.

Iloczyn geometryczny został po raz pierwszy krótko wspomniany przez Hermanna Grassmanna , który był głównie zainteresowany rozwojem blisko spokrewnionej algebry zewnętrznej . W 1878 roku William Kingdon Clifford znacznie rozszerzył prace Grassmanna, tworząc na jego cześć to, co obecnie zwykle nazywa się algebrami Clifforda (chociaż sam Clifford nazwał je „algebrami geometrycznymi”). Clifford zdefiniował algebrę Clifforda i jej iloczyn jako unifikację algebry Grassmanna i algebry kwaternionów Hamiltona . Dodanie duala iloczynu zewnętrznego Grassmanna („spotkanie”) pozwala na użycie algebry Grassmanna – Cayleya , a konforemna wersja tej ostatniej wraz z konforemną algebrą Clifforda daje konforemną algebrę geometryczną (CGA) zapewniającą ramy dla klasycznych geometrii . W praktyce te i kilka operacji pochodnych pozwalają na zgodność elementów, podprzestrzeni i operacji algebry z interpretacjami geometrycznymi. Przez kilka dziesięcioleci algebry geometryczne były nieco ignorowane, znacznie przyćmione przez rachunek wektorowy następnie nowo opracowany w celu opisania elektromagnetyzmu. Termin „algebra geometryczna” został ponownie spopularyzowany w latach 60. XX wieku przez Hestenesa , który opowiadał się za jego znaczeniem dla fizyki relatywistycznej.

Skalary i wektory mają swoją zwykłą interpretację i tworzą odrębne podprzestrzenie algebry geometrycznej. Dwuwektory zapewniają bardziej naturalną reprezentację wielkości pseudowektorów w algebrze wektorowej , takich jak zorientowany obszar, zorientowany kąt obrotu, moment obrotowy, moment pędu i pole elektromagnetyczne. Trójwektor reprezentować zorientowaną objętość i tak dalej. Element zwany ostrzem może służyć do reprezentowania podprzestrzeni i rzutów ortogonalnych ${\ displaystyle V}$ na tę podprzestrzeń. Obroty i odbicia są reprezentowane jako elementy. W przeciwieństwie do algebry wektorowej, algebra geometryczna naturalnie przyjmuje dowolną liczbę wymiarów i dowolną formę kwadratową, na przykład w teorii względności .

Przykłady algebr geometrycznych stosowanych w fizyce obejmują algebrę czasoprzestrzeni (i mniej powszechną algebra przestrzeni fizycznej ) oraz konforemną algebrę geometryczną . Rachunek geometryczny , rozszerzenie GA, które obejmuje różniczkowanie i całkowanie , może być wykorzystywane do formułowania innych teorii, takich jak analiza zespolona i geometria różniczkowa , np. przy użyciu algebry Clifforda zamiast form różniczkowych . Algebra geometryczna była propagowana, w szczególności przez David Hestenes i Chris Doran jako preferowane ramy matematyczne dla fizyki . Zwolennicy twierdzą, że zapewnia on zwięzłe i intuicyjne opisy w wielu dziedzinach, w tym klasycznej i kwantowej , teorii elektromagnetycznej i teorii względności . GA znalazła również zastosowanie jako narzędzie obliczeniowe w grafice komputerowej i robotyce .

Definicja i notacja

Istnieje wiele różnych sposobów definiowania algebry geometrycznej. Oryginalne podejście Hestenesa było aksjomatyczne, „pełne geometrycznego znaczenia” i równoważne z uniwersalną algebrą Clifforda. $skończenie$ wymiarową przestrzeń kwadratową nad polem o symetrycznej postaci dwuliniowej ( $iloczyn$ wewnętrzny , np euklidesowa lub lorentzowska ) $:V\razy V\do F}$${\ displaystyle$ , algebra geometryczna dla tej przestrzeni kwadratowej to algebra Clifforda ${\ Displaystyle \ operatorname {Cl} (V, g)}$ . $Jak zwykle w tej$ , w pozostałej części tego artykułu będzie tylko rzeczywisty przypadek Notacja ${\ Displaystyle {\ mathcal {G}} (p, q)}$ (odpowiednio ${\ Displaystyle {\ mathcal {G}} (p, q, r)} )$ będzie użyte do oznaczenia algebry geometrycznej, dla której $forma$ ma sygnaturę ${\ Displaystyle (p, q)}$ (odpowiednio ${\ Displaystyle (p, q, r)}$ ).

Podstawowy iloczyn algebry nazywany jest iloczynem geometrycznym , a iloczyn zawartej algebry zewnętrznej nazywany jest iloczynem zewnętrznym (często nazywany iloczynem klinowym , rzadziej iloczynem zewnętrznym ). Standardowo oznacza się je odpowiednio przez zestawienie (tj. pomijanie jakiegokolwiek wyraźnego symbolu mnożenia) i symbol ${\ displaystyle \ klin}$ . Powyższa definicja algebry geometrycznej jest abstrakcyjna, więc podsumowujemy właściwości iloczynu geometrycznego za pomocą następującego zestawu aksjomatów. Iloczyn geometryczny ma następujące właściwości, ponieważ ${\ Displaystyle A, B, C \ in {\ mathcal {G}} (p, q)$ :

• ${\ Displaystyle AB \ w {\ mathcal {G}} (p, q)}$ ( zamknięcie )
• $Displaystyle 1A = A1 = A}$$\$ , gdzie elementem tożsamości (istnienie elementu tożsamości )
• $\ Displaystyle A (BC) = (AB) C}$ ( asocjatywność )
• ${\ Displaystyle A (B + C) = AB + AC}$ i ${\ Displaystyle (B + C) A = BA +CA}$ ( rozdzielność )
• $a ^ {2} = g (a, a) 1$$a}$ , gdzie jest dowolnym elementem algebry $\ Displaystyle$ { .

Produkt zewnętrzny ma te same właściwości, z wyjątkiem tego, że ostatnia właściwość powyżej jest zastąpiona przez ${\ displaystyle a \ klin a = 0}$ dla ${\ displaystyle a \ in V}$ .

$,$ że w ostatniej powyższej właściwości liczba rzeczywista być nieujemna $,$ określona Ważną właściwością iloczynu geometrycznego jest istnienie elementów posiadających multiplikatywną odwrotność. $Displaystyle$ wektora , jeśli istnieje i jest równy $a ^ {2} \ neq 0},$ to $}$${\ Displaystyle g (a, a) ^ {- 1} a}$ . Niezerowy element algebry niekoniecznie ma multiplikatywną odwrotność. Na przykład, jeśli jest wektorem w taki sposób, że $,$$u ^ {2} = 1}$$\textstyle {\frac {1}{2}}(1+u)}$$Displaystyle$ element ${\$ jest zarówno nietrywialne idempotentny element i niezerowy dzielnik zera , a zatem nie ma odwrotności.

Zwykle identyfikuje się i ${\ displaystyle$$V} z$${\ Displaystyle \ mathbb {R} \ do {\ mathcal {G}} (p, q)}$ obrazami pod naturalnymi osadami i ${\ Displaystyle V \ do {\ mathcal {G}} (p, q)}$ . W tym artykule zakłada się tę identyfikację. W całym tekście terminy skalar i wektor odnoszą się odpowiednio do elementów i ( $.$ ich obrazów pod tym $osadzeniem$

Produkt geometryczny

Główne artykuły: Symetryczna postać dwuliniowa i algebra zewnętrzna

Biorąc pod uwagę dwa wektory i ${ \ displaystyle$$\ displaystyle ab}$$}$ , jeśli iloczyn geometryczny jest antyprzemienny; za są prostopadłe (u góry), ponieważ za $\ Displaystyle a \ cdot b = 0}$ , jeśli jest przemienne; są równoległe (na dole), ponieważ ${\ Displaystyle a \ klin b = 0}$ .

Orientacja zdefiniowana przez uporządkowany zestaw wektorów.

Odwrócona orientacja odpowiada zanegowaniu zewnętrznego produktu.

Geometryczna interpretacja stopni $-$ w rzeczywistej algebrze zewnętrznej dla $($ ze znakiem), skierowany odcinek linii lub wektor), $} displaystyle 2}$$\ displaystyle$ (zorientowany element płaszczyzny), ${\ displaystyle 3}$ (zorientowana objętość). Zewnętrzny iloczyn wektorów można zwizualizować jako dowolny -wymiarowy kształt (np. $displaystyle$$n}$${\ Displaystyle n}$ - równoległobok , ${\ Displaystyle n}$ - elipsoida ); z wielkością ( hiperobjętość ) i orientacją określoną przez jego $-wymiarową$ granicę i po której

Dla wektorów ${\ displaystyle$ b $b}$ możemy zapisać iloczyn geometryczny dowolnych dwóch wektorów $\ displaystyle a} i$ sumę iloczynu symetrycznego i iloczynu antysymetrycznego za { ${\ displaystyle b$ :

${\ Displaystyle ab = {\ Frac {1} {2}} (ab + ba) + {\ Frac {1} 2}} (ab-ba)}$

W ten sposób możemy zdefiniować iloczyn wewnętrzny wektorów jako

${\ Displaystyle a \ cdot b: = g (a, b)}$

tak, że iloczyn symetryczny można zapisać jako

${\ Displaystyle {\ Frac {1} {2}} (ab + ba) = { \frac {1}{2}}\left((a+b)^{2}-a^{2}-b^{2}\right)=a\cdot b}$

$zdeterminowany$ odwrotnie, jest całkowicie przez algebrę. Część antysymetryczna jest iloczynem zewnętrznym dwóch wektorów, iloczynem zawartej algebry zewnętrznej :

${\ Displaystyle a \ klin b: = {\ Frac {1} {2}} (ab-ba) = - (b \ klin a)}$

Następnie przez proste dodanie:

${\ Displaystyle ab = a \ cdot b + a \ klin b}$ niezgeneralizowana lub wektorowa postać iloczynu geometrycznego.

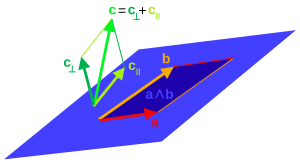
Iloczyny wewnętrzne i zewnętrzne są powiązane ze znanymi pojęciami ze standardowej algebry wektorów. Geometrycznie i są równoległe , jeśli ich iloczyn geometryczny jest równy ich iloczynowi wewnętrznemu, podczas gdy i $prostopadłe za$ { \ $displaystyle$$}$ b $\ displaystyle b}$ jeśli ich iloczyn geometryczny jest równy ich iloczynowi zewnętrznemu. W algebrze geometrycznej, dla której kwadrat dowolnego niezerowego wektora jest dodatni, iloczyn wewnętrzny dwóch wektorów można utożsamiać z iloczynem skalarnym standardowej algebry wektorów. Iloczyn zewnętrzny dwóch wektorów można utożsamić z obszarem ze znakiem otoczonym równoległobokiem , którego boki są wektorami. Iloczyn krzyżowy dwóch wektorów w $.$ o postaci kwadratowej dodatnio określonej jest ściśle powiązany z ich iloczynem zewnętrznym

Większość interesujących nas algebr geometrycznych ma niezdegenerowaną formę kwadratową. Jeśli forma kwadratowa jest całkowicie zdegenerowana , iloczyn wewnętrzny dowolnych dwóch wektorów wynosi zawsze zero, a algebra geometryczna jest wtedy po prostu algebrą zewnętrzną. O ile nie zaznaczono inaczej, w tym artykule omówimy tylko niezdegenerowane algebry geometryczne.

Produkt zewnętrzny jest naturalnie rozszerzony jako asocjacyjny dwuliniowy operator binarny między dowolnymi dwoma elementami algebry, spełniający tożsamości

${\ Displaystyle {\ rozpocząć {wyrównane} 1 \ klin a_ {i} & = a_ {i} \ klin 1 = a_ {i} \\ a_ {1} \ klin a_ {2} \ klin \ cdots \ klin a_ { r}&={\frac {1}{r!}}\sum _{\sigma \in {\mathfrak {S}}_{r}}\operatorname {sgn} (\sigma )a_{\sigma (1 )}a_{\sigma (2)}\cdots a_{\sigma (r)},\end{wyrównane}}}$

$}$ indeksów, przy czym znak permutacji i są wektorami ${\ Displaystyle \ operatorname {sgn} (\ sigma)$ nie ogólnych elementów algebry). Ponieważ każdy element algebry można wyrazić jako sumę iloczynów tej postaci, definiuje to iloczyn zewnętrzny dla każdej pary elementów algebry. Z definicji wynika, że ​​iloczyn zewnętrzny tworzy algebrę przemienną .

Ostrza, stopnie i podstawa kanoniczna

Multiwektor, który jest iloczynem zewnętrznym liniowo niezależnych wektorów, nazywany jest ostrzem i mówi się, że $displaystyle$ stopień $r}$ . Multiwektor, który jest sumą ostrzy stopnia, $displaystyle$ jest (jednorodnym) multiwektorem stopnia $r}$ . Z aksjomatów, z domknięciem, każdy multiwektor algebry geometrycznej jest sumą ostrzy.

${$ zestaw liniowo niezależnych wektorów $} \}}$ obejmujących ${\ displaystyle r}$ -wymiarowa podprzestrzeń przestrzeni wektorowej. Dzięki nim możemy zdefiniować rzeczywistą macierz symetryczną (w taki sam sposób jak macierz Gramiana )

${\ Displaystyle [\ mathbf {A}] _ {ij} = a_ {i} \ cdot a_ {j}}$

Zgodnie z twierdzeniem spektralnym $mathbf$ przez $ortogonalną można przeprowadzić$ diagonalną macierz diagonalną przez macierz ortogonalną ${A}}$

${\ Displaystyle \ suma _ {k, l} [\ mathbf {O}] _ {ik} [\ mathbf {A}] _ {kl} [\ mathbf {O} ^ {\ operatorname {T}}] _ { lj}=\suma _{k,l}[\mathbf {O}]_{ik}[\mathbf {O}]_{jl}[\mathbf {A}]_{kl}=[\mathbf {D } ]_{ij}}$

$Zdefiniuj$ nowy zestaw wektorów, macierz :

${j} [\ mathbf {O}] _ {ij} a_ {j}}$

Ponieważ transformacje ortogonalne zachowują iloczyny wewnętrzne, wynika z tego, że ${j} = [\ mathbf {D}] _ {ij}}$ e_ ${\ Displaystyle \ {e_ {1}, \ ldots, e_ {r} \}}$ są prostopadłe. Innymi słowy, iloczyn geometryczny dwóch różnych wektorów $\ neq e_ {j}}$ jest całkowicie określony przez ich produkt zewnętrzny lub bardziej ogólnie

${\ Displaystyle {\ rozpocząć {tablica} {rl} e_ {1} e_ {2} \ cdots e_ {r} i = e_ {1} \klin e_{2}\klin \cdots \klin e_{r}\\&=\left(\sum _{j}[\mathbf {O}]_{1j}a_{j}\right)\klin \ left(\sum _{j}[\mathbf {O}]_{2j}a_{j}\right)\klin \cdots \wedge \left(\sum _{j}[\mathbf {O}]_{ rj}a_{j}\right)\\&=(\det \mathbf {O} )a_{1}\klin a_{2}\klin \cdots \klin a_{r}\end{tablica}}}$

Dlatego każde ostrze klasy $iloczyn$ zapisać jako $wektorów$ . Mówiąc bardziej ogólnie, jeśli dozwolona jest zdegenerowana algebra geometryczna, wówczas macierz ortogonalna jest zastępowana macierzą blokową , która jest ortogonalna w niezdegenerowanym bloku, a macierz diagonalna ma wpisy o wartości zerowej wzdłuż zdegenerowanych wymiarów. Jeśli nowe wektory niezdegenerowanej podprzestrzeni zostaną znormalizowane zgodnie z

${\ Displaystyle {\ kapelusz {e}} _ {i} = {\ Frac {1} {\ sqrt {| e_ {i} \ cdot e_ {i}|}}} e_ {i},}$

wtedy te znormalizowane wektory muszą być kwadratowe do ${\ displaystyle + 1}$ lub ${\ displaystyle -1}$ . Zgodnie z $s$ bezwładności Sylwestra całkowita liczba s i całkowita liczba wzdłuż przekątnej macierzy $jest$ Co za tym idzie, całkowita liczba tych wektorów, które są kwadratowe do $displaystyle + 1},$$\$ oraz całkowita liczba p {\ ${\ displaystyle q}$ ten kwadrat do ${\ displaystyle -1}$ jest niezmienny. (Całkowita liczba wektorów bazowych, które są kwadratowe do zera, jest również niezmienna i może być różna od zera, jeśli dozwolony jest przypadek zdegenerowany). Oznaczamy tę algebrę $\ Displaystyle {\ mathcal {G}} (p, q)}$ . Na $_$ trójwymiarowej , _ ${\ Displaystyle {\ mathcal {G}} (1,3)}$ relatywistyczna czasoprzestrzeń i ${\ Displaystyle {\ mathcal {G}} (4,1)}$ konforemna algebra geometryczna trzech -wymiarowa przestrzeń.

Zbiór wszystkich możliwych iloczynów ortogonalnych $wektorów$ bazowych z indeksami w porządku rosnącym, w tym jako $iloczyn$ pusty, stanowi podstawę całej algebry geometrycznej (odpowiednik PBW . Na przykład poniższe jest podstawą algebry geometrycznej: ${\ Displaystyle {\ mathcal {G}} (3,0)$ }

${\ Displaystyle \ {1, e_ {1}, e_ {2} ,e_{3},e_{1}e_{2},e_{2}e_{3},e_{3}e_{1},e_{1}e_{2}e_{3}\}}$

Podstawa utworzona w ten sposób nazywana jest $kanoniczną$ podstawą algebry geometrycznej, a każda inna podstawa ortogonalna dla inną podstawę kanoniczną. Każda podstawa kanoniczna składa się z ${\ displaystyle 2 ^ {n}}$ . Każdy multiwektor algebry geometrycznej można wyrazić jako liniową kombinację kanonicznych elementów bazowych. Jeśli kanoniczne elementy bazowe to ${\ Displaystyle \ {B_ {i} \ mid i \ in S \}}$ z ${\ displaystyle S}$ będąc zbiorem indeksów, to iloczyn geometryczny dowolnych dwóch multiwektorów wynosi

${\ Displaystyle \ lewo (\ suma _ {i} \ alfa _ {i} B_ {i} \ prawej) \ lewo (\ suma _ {j} \ beta _ {j} B_ {j} \ prawej) = \ suma _{i,j}\alfa _{i}\beta _{j}B_{i}B_{j}.}$

Terminologia „ $celu$ opisania multiwektorów zawierających elementy tylko jednego stopnia. W przestrzeni o wyższych wymiarach niektóre takie multiwektory nie są ostrzami (nie można ich uwzględnić w iloczynie zewnętrznym wektorów ${\ displaystyle k}$ ). Na przykład ${\ Displaystyle e_ {1} \ klin e_ {2} + e_ {3} \ klin e_ {4}}$ w ${\ Displaystyle {\ mathcal {G}} (4,0)}$ nie może być uwzględniony; zazwyczaj jednak takie elementy algebry nie poddają się interpretacji geometrycznej jako obiekty, chociaż mogą reprezentować wielkości geometryczne, takie jak obroty. Tylko $Displaystyle 0,1 (n-1)}$${$$\$ i wektory są zawsze ostrzami w .

Projekcja stopnia

Korzystając z podstawy ortogonalnej, można ustanowić stopniowaną strukturę przestrzeni wektorowej . Elementy algebry geometrycznej, które są skalarnymi wielokrotnościami $1},$$displaystyle$ są ostrzami stopni i nazywane są skalarami . Multiwektory, które mieszczą się w przedziale od ${\ Displaystyle \ {e_ {1}, \ ldots, e_ {n} \}}$ są ostrzami klasy ${\ displaystyle 1}$ i są zwykłymi wektory. Multiwektory w rozpiętości $\ Displaystyle \ {e_ {i} e_ {j} \ mid 1 \ równoważnik i <j \ równoważnik n \}}$ są klasy ${\ Displaystyle 2}$ ostrza i są dwuwektorami. Ta terminologia jest kontynuowana do ostatniej klasy ${\ displaystyle n}$ . Alternatywnie, ostrza klasy- ${\ displaystyle n}$ nazywane są pseudoskalarami , klasa- ${\ displaystyle (n-1)}$ ostrza pseudowektory itp. Wiele elementów algebry nie jest ocenianych według tego schematu, ponieważ są one sumami elementów o różnym stopniu. O takich pierwiastkach mówi się, że są mieszane . Klasyfikacja multiwektorów jest niezależna od pierwotnie wybranej podstawy.

Jest to stopniowanie jako przestrzeń wektorowa, ale nie jako algebra. Ponieważ iloczyn ostrza $}$ ostrza jest zawarty w rozpiętości od ostrzy $r + s$$\$$displaystyle$ geometryczny algebra jest filtrowaną algebrą .

Multiwektor można rozłożyć za pomocą $}$$\displaystyle A}$$stopni$ , $wyprowadza$ A $displaystyle$ . W rezultacie:

${\ Displaystyle A = \ suma _ {r = 0} ^ {n} \ langle A \ rangle _ {r}}$

Na przykład iloczyn geometryczny dwóch wektorów za ${\ Displaystyle ab = a \ cdot b + a \ klin b = \ langle ab$ ponieważ ${\ Displaystyle \ langle ab \ rangle _ {0} = a \ cdot b}$ i ${\ Displaystyle \ langle ab \ rangle _ {2} = a \ klin b}$ i ${\ Displaystyle \ langle ab \ rangle _ {i} = 0}$ dla ${\ Displaystyle i}$ inny niż $i$ 2 {\ $2}$ .

Rozkład multiwektora $\ displaystyle A}$ również podzielić na składowe, które są parzyste i nieparzyste: ZA {

${\ Displaystyle A ^ {+} = \ langle A \ rangle _ {0} + \ langle A \ rangle _ {2} + \ langle A \ rangle _ {4} + \ cdots}$

${\ Displaystyle A ^ {-} = \ langle A \ rangle _ {1} + \ langle A\rangle _{3}+\langle A\rangle _{5}+\cdots }$

$Jest$ to wynikiem zapomnienia struktury z - stopniowanej $wektorowej$ do - przestrzeni . Produkt geometryczny respektuje tę grubszą gradację. Tak więc, oprócz tego, że jest - stopniowaną przestrzenią wektorową , algebra geometryczna jest - $Displaystyle \ operatorname {Z} _ {2}}$$-$ stopniowaną algebrą lub superalgebra .

Ograniczając się do części parzystej, iloczyn dwóch parzystych elementów jest również parzysty. Oznacza to, że parzyste multiwektory definiują parzystą podalgebrę . Parzysta podalgebra $-wymiarowej$ algebry geometrycznej jest izomorficzna (bez zachowania filtracji lub stopniowania) z pełną algebrą geometryczną o wymiarach $)} .$ Przykłady obejmują ${\ Displaystyle {\ mathcal {G}} ^ {+} (2,0) \ cong {\ mathcal {G}} (0,1)}$ i ${ \ Displaystyle {\ mathcal {G}} ^ {+} (1,3) \ cong {\ mathcal {G}} (3,0)}$ .

Reprezentacja podprzestrzeni

Algebra geometryczna reprezentuje podprzestrzenie jako ostrza, więc współistnieją w tej samej algebrze z wektorami z $V}$$displaystyle$ . ZA ${\ displaystyle k}$ -wymiarowa podprzestrzeń z ${$$\ displaystyle V}$ jest reprezentowana przez ortogonalną podstawę $},b_{2},\ldots,b_{k}\}}$${\ Displaystyle \ {b_ {$ i używając iloczynu geometrycznego do utworzenia ostrza ${\ Displaystyle D = b_ {1} b_ {2} \ cdots b_ {k}}$ . Istnieje wiele ostrzy reprezentujących ${\ displaystyle W}$ ; wszystkie reprezentujące są $wielokrotnościami$$_$ Ostrza te można podzielić na dwa zestawy: dodatnie wielokrotności i ujemne wielokrotności $D$$}$ . Mówi się $że$ dodatnie wielokrotności $mają$ tę samą orientację co , a ujemne wielokrotności orientacji .

Ostrza są ważne, ponieważ operacje geometryczne, takie jak projekcje, obroty i odbicia, zależą od faktoryzacji za pośrednictwem produktu zewnętrznego, który zapewnia (ograniczona klasa) -ostrzy, $\ displaystyle n$ (uogólniona klasa) stopnia- $} displaystyle n}$ multiwektory nie, gdy ${\ displaystyle n \ geq 4}$ .

Pseudoskalary jednostkowe

Pseudoskalary jednostek to ostrza, które odgrywają ważną rolę w GA. Jednostką pseudoskalarną dla niezdegenerowanej podprzestrzeni z $jest ostrze$${\ displaystyle V}$ które jest iloczynem członków podstawy ortonormalnej dla ${\ displaystyle W}$ . Można pokazać $są$ oba $pseudoskalarami$ jednostkowymi $,$ to ${\ Displaystyle I = \ pm I'}$${\ Displaystyle I ^ {2} = \ pm 1}$ ja . Jeśli ktoś nie wybierze podstawy ortonormalnej dla $.$ to osadzanie Plückera daje wektor w algebrze zewnętrznej, ale tylko do skalowania $\ alpha \ neq 0}$ izomorfizmu przestrzeni wektorowej między algebrą geometryczną a algebrą zewnętrzną, daje to klasę równoważności dla wszystkich $displaystyle$ . Ortonormalność eliminuje tę niejednoznaczność, z wyjątkiem powyższych znaków.

utworzona jest algebra geometryczna $Displaystyle$ znanym dodatnio określonym iloczynem wewnętrznym na $\ mathbb {R} ^ {n$ . Biorąc pod uwagę $,$ (dwuwymiarową podprzestrzeń) można znaleźć podstawę ortonormalną $\ Displaystyle \ {b_ {1}, b_ {2}\}}$ rozciągających się na płaszczyźnie, a tym samym znaleźć jednostkę pseudoskalarną ${\ Displaystyle I = b_ {1} b_ {2}}$ reprezentujący tę płaszczyznę. Iloczyn geometryczny dowolnych dwóch wektorów w rozpiętości i ${\ Displaystyle b_ {2}$${\ alfa _ {0} + \ alfa _ {1} I \ mid \ alfa _ {i} \ in \ mathbb {R} \}} , czyli jest to$$leży$ w ${\ Displaystyle$ suma wektora za { $\ displaystyle 0}$ i ${\ Displaystyle 2}$ -wektor.

Z właściwości iloczynu geometrycznego ${\ Displaystyle I ^ {2} = b_ {1} b_ {2} b_ {1}b_{2}=-b_{1}b_{2}b_{2}b_{1}=-1}$ . Podobieństwo do jednostki urojonej nie jest przypadkowe: podprzestrzeń ${\ Displaystyle \ {\ alfa _ {0} + \ alfa _ {1} ja \ środkowy \ alfa _ {i} \ w \ mathbb {R} \}} jest R {\ Displaystyle \ mathbb {$ R $}$ - algebra izomorficzna z liczbami zespolonymi . W ten sposób kopia liczb zespolonych jest osadzona w algebrze geometrycznej dla każdej dwuwymiarowej podprzestrzeni, $której$ forma kwadratowa jest określona.

Czasami możliwe jest zidentyfikowanie obecności jednostki urojonej w równaniu fizycznym. Takie jednostki wynikają z jednej z wielu wielkości w algebrze rzeczywistej, które są kwadratowe do $,$ mają znaczenie geometryczne ze względu na właściwości algebry i interakcje jej różnych podprzestrzeni

W ${\ Displaystyle {\ mathcal {G}} (3,0)}$ występuje kolejny znany przypadek. Biorąc pod uwagę podstawę kanoniczną składającą się z wektorów ortonormalnych $\ displaystyle e_ {i$$}$ wszystkich $}$ mi ja {

${\ Displaystyle \ {e_ {3} e_ {2}, e_ {1} e_ {3}, e_ {2} e_ {1} \}.}$

Oznaczając te $jot$ chwilowo odbiegając od naszej konwencji wielkich liter), podprzestrzeń generowaną przez $i} ,$ i $- ja$ { $\ displaystyle$$displaystyle j} i$ - wektory to dokładnie ${\ Displaystyle \ {\ alfa _ {0} + i \ alfa _ {1} + J \ alfa _ {2} + k \ alfa _ {3} \ środkowy \ alfa _ {i} \ w \ mathbb {R} \}}$ . Ten zestaw jest postrzegany jako parzysta podalgebra $}$ a ponadto jest izomorficzny jako -algebra ${\ Displaystyle {\ mathcal {G}} (3,0)$ do kwaternionów , innego ważnego systemu algebraicznego.

Rozszerzenia produktów wewnętrznych i zewnętrznych

Powszechną praktyką jest rozszerzanie iloczynu zewnętrznego na wektory na całą algebrę. Można tego dokonać za pomocą wspomnianego powyżej projekcji stopnia :

${\ Displaystyle C \ klin D: = \ suma _ {r, s} \ langle \ langle C \ rangle _ {r} \langle D\rangle _{s}\rangle _{r+s}}$ ( produkt zewnętrzny )

To uogólnienie jest zgodne z powyższą definicją dotyczącą antysymetryzacji. Innym uogólnieniem związanym z iloczynem zewnętrznym jest iloczyn komutatora:

${\ Displaystyle C \ razy D: = {\ tfrac {1} {2}} (CD-DC)}$ ( iloczyn komutatora )

Produkt regresywny (zwykle określany jako „spotkanie”) jest dualny produktu zewnętrznego (lub „łączenia” w tym kontekście). Podwójna specyfikacja elementów pozwala, dla ostrzy i $displaystyle$$B}$ , na przecięcie (lub spotkanie), w którym dualność ma być wzięta w stosunku do ostrza o najmniejszym stopniu, zawierającego zarówno ${\ displaystyle A$ i ( $łączenie$ )

${\ Displaystyle C \ vee D: = ((CI ^ {- 1}) \ klin (DI ^ {- 1})) I}$

z $pseudoskalarną$ algebry. Produkt regresywny, podobnie jak produkt zewnętrzny, jest asocjacyjny.

Iloczyn wewnętrzny na wektorach można również uogólnić, ale na więcej niż jeden nierównoważny sposób. Artykuł ( Dorst 2002 ) zawiera pełne omówienie kilku różnych iloczynów wewnętrznych opracowanych dla algebr geometrycznych i ich wzajemnych powiązań, z których zaczerpnięto notację. Wielu autorów używa tego samego symbolu, co dla iloczynu wewnętrznego wektorów dla wybranego przez siebie rozszerzenia (np. Hestenes i Perwass). Nie pojawił się żaden spójny zapis.

Wśród tych kilku różnych uogólnień iloczynu wewnętrznego na wektorach są:

${\ Displaystyle C \; \ rfloor \; D: = \ suma _ {r, s} \ langle \ langle C \ rangle _{r}\langle D\rangle _{s}\rangle _{sr}}$ ( lewe skrócenie )

${\ Displaystyle C \; \ lfloor \; D: = \ suma _ {r, s} \ langle \ langle C \ rangle _ {r} \ langle D \ rangle _ {s} \ rangle _ {rs} }$ ( skurcz prawy )

${\ Displaystyle C * D: = \ suma _ {r, s} \ langle \ langle C \ rangle _ { r}\langle D\rangle _{s}\rangle _{0}}$ ( iloczyn skalarny )

${\ Displaystyle C \ punktor D: = \ suma _ {r, s} \ langle \ langle C \ rangle _ {r} \ langle D \ rangle _ {s} \ rangle _ {| sr |}} („$ ( produkt tłuszczowy) kropka)

Dorst (2002) argumentuje za stosowaniem skróceń zamiast iloczynu wewnętrznego Hestenesa; są algebraicznie bardziej regularne i mają czystsze interpretacje geometryczne. Wiele tożsamości zawierających skróty jest ważnych bez ograniczeń ich danych wejściowych. Na przykład,

${\ Displaystyle C \; \ rfloor \; D = (C \ klin (DI ^ {-1})) ja}$

${\ Displaystyle C \; \ lfloor \; D = ja ((I ^ {- 1} C) \ klin D)}$

${\ Displaystyle (A \ klin B) * C = A * (B \; \ rfloor \; C)} do ∗$

$Displaystyle C * (B \ klin ZA) = (C \; \ lfloor \; B) * A}$

${\ Displaystyle A \; \ rfloor \; (B \; \ rfloor \;$

${\ Displaystyle (A \; \ rfloor \; B) \; \ lfloor \; C = A \; \ rfloor \; (B \; \ lfloor \; C).}$

$z$${\ Displaystyle aB = a \; \ rfloor \; B + a \ klin B}$ przedłużenia iloczynu wewnętrznego na wektorach obejmują do dla dowolnego wektora $displaystyle$ multiwektora $a}$ i że P. ${\ Displaystyle {\ mathcal {P}} _ {b} (a) = (a \ cdot b ^ {-1}) b}$ jest do ${\ Displaystyle {\ mathcal {P}} _ {B} (A) = (A \; \ rfloor \; B ^ {- 1}) \; \ rfloor \; B}$ dla dowolnego ostrza ${\ displaystyle B}$ i dowolny multiwektor $z$ niewielką modyfikacją w celu uwzględnienia wartości $.$ podanej poniżej )

Podwójna podstawa

Niech ${\ Displaystyle \ {e_ {1}, \ ldots, e_ {n} \}}$ będzie podstawą ${\ Displaystyle V}$ , tj. zbiorem ${\ displaystyle n }$${\ displaystyle V$ niezależne wektory, które obejmują -wymiarową przestrzeń wektorową $}$ . Podstawa podwójna ${\ Displaystyle \ {e_ {1}, \ ldots, e_ {n} \}}$ to zbiór elementów podwójnej przestrzeni wektorowej ${\ Displaystyle V ^ {*}}$ , który tworzy system biotogonalny na tej podstawie, będąc w ten sposób elementami oznaczonymi jako satysfakcjonujące ${\ Displaystyle \ {e ^ {1}, \ ldots, e ^ {n} \}}$

${\ Displaystyle e ^ {i} \ cdot e_ {j} = \ delta ^ {i} {} _ {j},}$

gdzie jest $deltą$ . _

$,$ niezdegenerowaną formę kwadratową na , zostaje naturalnie utożsamiana z ${\ displaystyle V}$ a podwójna podstawa może być uważana za elementy $}$$}$$\ displaystyle$ , ale generalnie nie są tym samym zestawem, co oryginalna baza.

$niech$ uwagę dalej GA ,

${\ Displaystyle I = e_ {1} \ klin \ cdots \ klin e_ {n}}$

${\ Displaystyle \ {e_ {1}, \ ldots, e_ {$ niekoniecznie jest kwadratem do kwadratu ) utworzonym z podstawy ${$ . Wektory o podwójnej podstawie można skonstruować jako

${\ Displaystyle e ^ {i} = (-1) ^ {i-1} (e_ {1}\klin \cdots \klin {\check {e}}_{i}\klin \cdots \klin e_{n})I^{-1},}$

gdzie ${\ displaystyle {\ check {e}} _ {i}}$ oznacza, że $bazowy$ jest pomijany w produkcie.

Podwójna podstawa jest również znana jako podstawa wzajemna lub rama wzajemna.

Głównym zastosowaniem podwójnej podstawy jest rozdzielanie wektorów na składowe. Biorąc pod uwagę wektor , składniki skalarne można zdefiniować jako za $i}}$$\ displaystyle a ^$

${\ Displaystyle a ^ {i} = a \ cdot e ^ {i} \,}$

pod względem których $jako$ rozdzielić na składowe wektorowe

${\ Displaystyle a = \ suma _ {i} a ^ {i} e_ {i} \ .}$

Możemy również zdefiniować $komponenty$

${\ Displaystyle a_ {i} = a \ cdot e_ {i} \,}$

pod względem których $wektorowe$ pod względem podwójnej podstawy as

${\ Displaystyle a = \ suma _ {i} a_ {i} e ^ {i} \ .}$

Podwójna podstawa, jak zdefiniowano powyżej, dla podprzestrzeni wektorowej algebry geometrycznej może zostać rozszerzona na całą algebrę. Dla zwięzłości użyjemy jednej dużej litery do przedstawienia uporządkowanego zestawu indeksów wektorowych. Czyli pisanie

${\ Displaystyle J = (j_ {1}, \ kropki, j_ {n}) \,}$

gdzie ${\ Displaystyle j_ {1}<j_ {2}<\ kropki <j_ {n}}$ możemy zapisać ostrze bazowe jako

${\ Displaystyle e_ {J} = e_ {j_ {1}} \ klin e_ {j_ {2}} \ klin \ cdots \ klin e_ {j_ {n}} \ .}$

Odpowiednie ostrze wzajemne ma indeksy w odwrotnej kolejności:

${\ Displaystyle e ^ {J} = e ^ {j_ {n}} \ klin \ cdots \ klin e ^ {j_ {2}} \ klin e ^ {j_ {1}} \ .}$

Podobnie jak w powyższym przypadku z wektorami, można to pokazać

${\ Displaystyle e ^ {J} * e_ {K} = \ delta _ {K} ^ {J} \,$

gdzie jest iloczynem skalarnym. ${\ displaystyle *}$

Mając $jako$ , możemy teraz zdefiniować komponenty skalarne

${\ Displaystyle A ^ {J} = A * e ^ {J} \,}$

pod względem którego $jako$ podzielić na ostrza składowe

${\ Displaystyle A = \ suma _ {J} A ^ {J} e_ {J} \ .}$

Możemy alternatywnie zdefiniować komponenty skalarne jako. ${\ displaystyle A_ {J}}$

${\ Displaystyle A_ {J} = A * e_ {J} \,}$

pod względem którego $jako$ podzielić na ostrza składowe

${\ Displaystyle A = \ suma _ {J} A_ {J} e ^ {J} \ .}$

Funkcje liniowe

Chociaż wersor jest łatwiejszy w obsłudze, ponieważ można go bezpośrednio przedstawić w algebrze jako multiwektor, wersory są podgrupą funkcji liniowych na multiwektorach, których nadal można używać w razie potrzeby. Algebra geometryczna $przestrzeni$$elementów$ obejmuje . Jeśli multiwektor jest reprezentowany przez rzeczywistą macierz kolumnową ${\ Displaystyle 2 ^ {n} \ razy 1}$$wyrazić$ podstawy algebry, to wszystkie liniowe przekształcenia multiwektora można przez rzeczywistą macierz Jednak taka ogólna transformacja liniowa umożliwia dowolne wymiany między stopniami, takie jak „obrót” skalara w wektor, który nie ma oczywistej interpretacji geometrycznej.

Interesująca jest ogólna transformacja liniowa z wektorów na wektory. Z naturalnym ograniczeniem zachowania indukowanej algebry zewnętrznej, morfizm zewnętrzny transformacji liniowej jest unikalnym rozszerzeniem wersora. Jeśli jest funkcją liniową, która odwzorowuje wektory na wektory, to jej morfizm zewnętrzny jest funkcją zgodną z regułą ${\ displaystyle f}$

${\ Displaystyle {\ podkreślenie {\ mathsf {f}}} (a_ {1}\klin a_{2}\klin \cdots \klin a_{r})=f(a_{1})\klin f(a_{2})\klin \cdots \klin f(a_{r}) }$

dla ostrza, rozciągnięty na całą algebrę poprzez liniowość.

Geometrie modelowania

Chociaż wiele uwagi poświęcono CGA, należy zauważyć, że GA nie jest tylko jedną algebrą, ale należy do rodziny algebr o tej samej zasadniczej strukturze.

Wektorowy model przestrzeni

Główny artykuł: Porównanie algebry wektorów i algebry geometrycznej

${\ Displaystyle {\ mathcal {G}} (3,0)}$ można uznać za rozszerzenie lub uzupełnienie algebry wektorów .

Parzysta podalgebra z jest izomorficzna z liczbami zespolonymi , co można zobaczyć zapisując wektor pod względem jego ${\ Displaystyle {\ mathcal {G}} (2,0$$)$ składniki w bazie ortonormalnej i pozostawione pomnożenie przez wektor bazowy ${\ displaystyle e_ {1}$ }

$Z = e_ {1} P = e_ {1} (xe_ {1} }+ye_{2})=x(1)+y(e_{1}e_{2}),}$

gdzie identyfikujemy ${\ Displaystyle i \ mapsto e_ {1} e_ {2}}$ od

${\ Displaystyle (e_ {1} e_ {2}) ^ {2} = e_ { 1}e_{2}e_{1}e_{2}=-e_{1}e_{1}e_{2}e_{2}=-1.}$

Podobnie $parzysta$$podalgebra$ podstawą izomorficzne z czwartorzędami , co można zobaczyć identyfikując ${\ Displaystyle i \ mapsto -e_ {2}e_ {3}}$ , ${\ Displaystyle j \ mapsto -e_ {3}e_ {1}}$ i ${\ styl wyświetlania k\mapsto -e_{1}e_{2}}$ .

Każda algebra asocjacyjna ma reprezentację macierzową; zastąpienie trzech kartezjańskich wektorów bazowych macierzami Pauliego daje reprezentację : ${\ Displaystyle {\ mathcal {G}} (3,0)$ }

${\ Displaystyle {\ rozpocząć {wyrównane} e_ {1} = \ sigma _ {1} = \ sigma _ {x} & = {\ rozpocząć {pmatrix} 0 i 1 \\ 1 & 0 \ koniec {pmatrix}} \\ e_ {2 }=\sigma _{2}=\sigma _{y}&={\begin{pmatrix}0&-i\\i&0\end{pmatrix}}\\e_{3}=\sigma _{3}=\ sigma _{z}&={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}\,.\end{wyrównane}}}$

Kropkowanie „ wektora Pauliego ” ( diada ):

$b$${3}}$ z dowolnymi wektorami $)$ za :

${\ Displaystyle \ sigma = \ sigma _ {1} e_ {1} + \ sigma _ {2} e_ {2} + \ sigma _ {3}$

${\ Displaystyle (\ sigma \ cdot a) (\ sigma \ cdot b) = a \ cdot b + a \ klin b} ($ Równoważnie, przez kontrolę, $\ Displaystyle a\cdot b+i\sigma \cdot (a\times b)}$ )

Model czasoprzestrzenny

W fizyce głównymi zastosowaniami są algebra geometryczna $rzadziej$ 1 , zwana algebrą czasoprzestrzenną lub ${\ Displaystyle {\ mathcal {G}} (3,0)}$ zinterpretował algebrę przestrzeni fizycznej (APS).

STA punkty czasoprzestrzeni są reprezentowane po prostu $czasoprzestrzeni -wymiarowej$ wektory, w APS punkty tego reprezentowane przez trójwymiarowy wektor (przestrzeń) plus jednowymiarowy skalar (czas).

W algebrze czasoprzestrzeni tensor pola elektromagnetycznego ma dwuwektorową reprezentację ${\ Displaystyle {F} = ({E} + ic {B}) \ gamma _ {0}}$ . Tutaj ja $\ Displaystyle i = \ gamma _ {0} \ gamma _ {1} \ gamma _ {2} \ gamma _ {3}}$ to jednostka pseudoskalarna (lub cztery wymiarowy element objętości), $a$ wektorem jednostkowym w kierunku czasu, $displaystyle$$}$ i są klasycznymi wektorami pola elektrycznego i magnetycznego (ze składową czasu zerowego). Używając czterech prądów $się$ równania Maxwella stają wtedy

Sformułowanie	Równania jednorodne	Równania niejednorodne
Pola	${\ Displaystyle DF = \ mu _ {0} J}$
	${\ Displaystyle D \ klin F = 0}$	${\ Displaystyle D ~ \ rfloor ~ F = \ mu _ {0} J}$
Potencjały (dowolny wskaźnik)	${\ Displaystyle F = D \ klin A}$	${\ Displaystyle D ~ \ rfloor ~ (D \ klin A) = \ mu _ {0} J}$
Potencjały (miernik Lorenza)	${\ Displaystyle F = DA}$ ${\ Displaystyle D ~ \ rfloor ~ A = 0}$	${\ Displaystyle D ^ {2} A = \ mu _ {0} J}$

W rachunku geometrycznym zestawienie wektorów, takie jak w $wskazuje$ iloczyn geometryczny i można je rozłożyć na części jako $D ~ \ rfloor ~ F + D\klin F}$ . Tutaj $.$$płaskiej$ w dowolnej czasoprzestrzeni i redukuje się do czasoprzestrzeni gdzie ${\ Displaystyle \ bigtriangledown}$ odgrywa rolę w czasoprzestrzeni Minkowskiego, która jest równoznaczna z rolą $w$ przestrzeni euklidesowej $Displaystyle$$}$ i jest powiązana z d'Alembertianem przez ${\ Displaystyle \ Box = \ bigtriangledown ^ {2}}$ . Rzeczywiście, biorąc pod uwagę obserwatora reprezentowanego przez wskazujący na przyszłość wektor podobny do czasu, mamy ${\ displaystyle \ gamma _ {0}}$

${\ Displaystyle \ gamma _ {0} \ cdot \ bigtriangledown = {\ Frac {1} {c}} {\ Frac {\ częściowy} {\ częściowy t}}}$

${\ Displaystyle \ gamma _ {0} \ klin \ bigtriangledown = \ nabla}$

Wzmocnienia w $co$ lorentzowskiej przestrzeni metrycznej mają to samo wyrażenie, $.$ w przestrzeni euklidesowej, gdzie jest dwuwektorem generowanym przez czas i związane z tym kierunki , podczas gdy w przypadku euklidesowym jest to dwuwektor generowany przez dwa kierunki przestrzenne, wzmacniający „analogię” do niemal identyczności.

Macierze Diraca są reprezentacją $używanymi$ pokazującą równoważność z

Model jednorodny

Rzutowa algebra geometryczna (PGA), znana również jako model jednorodny, zapewnia kompletną algebrę zawierającą reprezentacje wszystkich izometrii euklidesowych i podprzestrzeni liniowych, na których działają. W tym modelu pojedynczy zdegenerowany wymiar jest dodawany do n zwykłych wymiarów przestrzeni w celu utworzenia algebry ${\ Displaystyle {\ mathcal {G}} (n, 0,1)$ } Kompleksowe traktowanie ${\ Displaystyle {\ mathcal {G}} (3,0,1)}$ w szczególności podaje Lengyel . W trójwymiarowej PGA wektory odpowiadają punktom, dwuwektory odpowiadają liniom, a trójwektory odpowiadają płaszczyznom. Właściwe izometrie euklidesowe, które zawsze są ruchami śrub w przestrzeni 3D, są reprezentowane przez silniki składające się z ośmiu składowych parzystych, a niewłaściwe izometrie euklidesowe, które zawierają odbicie, są reprezentowane przez flektory składające się z ośmiu składowych nieparzystych. Algebra motoryczna jest poprawnym uogólnieniem podwójnych kwaternionów na pełny zbiór obiektów występujących w PGA.

Główną koncepcją w PGA jest symetria, która powstaje poprzez odwrócenie wektorów bazowych, które są obecne i nieobecne w każdym z komponentów obiektu. Powoduje to nie tylko fundamentalną dwoistość obiektów geometrycznych algebry, ale także operacje na tych obiektach. Każdy iloczyn w algebrze (iloczyn klina, iloczyn wewnętrzny, iloczyn geometryczny, iloczyn wewnętrzny) ma pasujący „antyprodukt”, który wykonuje tę samą operację na liczbach podwójnych swoich operandów. Włączenie obu rodzajów produktów jest niezbędne do ukończenia algebry. Operacje łączenia i łączenia między różnymi geometriami są wykonywane odpowiednio przez iloczyn klina i jego podwójny produkt przeciwklinowy. Iloczyn wewnętrzny i jego podwójny dają dwie różne normy, zwane normą masową i normą wagową, które wytwarzają odpowiednio wielkości skalarne i antyskalarne. Izometrie euklidesowe są wykonywane przez geometryczny antyprodukt.

Wszystkie obiekty w rzutowej algebrze geometrycznej są jednorodne, w tym wielkości, które byłyby po prostu skalarami w ustawieniach nierzutowych. Mnożenie dowolnego punktu, linii, płaszczyzny, silnika lub flektora przez niezerowy skalar nie ma wpływu na jego znaczenie. Obiekt jest rzutowany na przestrzeń 3D w procesie zwanym unityzacją , który sprawia, że ​​zbiorczy rozmiar komponentów rozciągających się do zdegenerowanej jedności wymiarowej. Konkretne pomiary odległości powstają jako jednorodne wielkości określone przez normę geometryczną, która jest sumą normy objętościowej i normy wagowej. Kiedy norma geometryczna jest ujednolicona, jej składnik skalarny reprezentuje rzeczywistą odległość.

Model konformalny

Główny artykuł: Konforemna algebra geometryczna

Pracując w GA, przestrzeń euklidesowa $sol$ wraz z konforemnym punktem w nieskończoności) jest rzutowo osadzona w CGA $displaystyle {\ mathcal {G}}(4,1)}$ poprzez identyfikację punktów euklidesowych z podprzestrzeniami 1D w stożku zerowym 4D podprzestrzeni wektora 5D CGA. Pozwala to na wykonywanie wszystkich przekształceń konforemnych jako obrotów i odbić i jest kowariantne , rozszerzając relacje padania geometrii rzutowej na okręgi i sfery.

W szczególności dodajemy ortogonalne wektory bazowe $displaystyle e_ {-}$ mi $}$ takie, że ${\ displaystyle e_ {+} ^ {2} = +1 }$ i ${\ Displaystyle e_ {-} ^ {2} = -1}$ do podstawy przestrzeni wektorowej, która generuje ${\ Displaystyle {\ mathcal {G}} (3, 0)}$ i zidentyfikować wektory zerowe

${\ Displaystyle n_ {\ infty} = e_ {-} + e_ {+}}$ jako punkt konformalny w nieskończoności (patrz Kompaktowanie ) i

${\ Displaystyle n _ {\ text {o}} = {\ tfrac {1}{2}} (e_ {-} -e_ {+})}$ jako punkt pochodzenia, dając

${\ Displaystyle n _ {\ infty} \ cdot n _ {\ tekst {o}} = -1}$ .

Ta procedura ma pewne podobieństwa do procedury pracy ze współrzędnymi jednorodnymi w geometrii rzutowej iw tym przypadku umożliwia modelowanie transformacji euklidesowych jako ortogonalnych transformacji podzbioru $} ^ {3}}$${\ Displaystyle \ mathbf {R} ^ {4,1}}$ .

Szybko zmieniający się i płynny obszar GA, CGA, jest również badany pod kątem zastosowań w fizyce relatywistycznej.

Modele transformacji projekcyjnej

Obecnie bada się dwóch potencjalnych kandydatów jako podstawę geometrii afinicznej ${\mathcal {R}}(4,4)}$$4$ R $\$ , który obejmuje reprezentacje ścinania i niejednorodnego skalowania, a także powierzchnie czworokątne i przekroje stożkowe .

Nowy model badawczy, Quadric Conformal Geometric Algebra (QCGA) $jest$ kwadratowym Chodzi o to, aby reprezentować obiekty w niskowymiarowych podprzestrzeniach algebry. QCGA jest w stanie konstruować kwadratowe powierzchnie przy użyciu punktów kontrolnych lub niejawnych równań. Co więcej, QCGA może obliczyć przecięcie powierzchni kwadratu, jak również wektory stycznej i normalnej powierzchni w punkcie leżącym na powierzchni kwadratu.

Interpretacja geometryczna

Projekcja i odrzucenie

W przestrzeni 3D dwuwektor definiuje podprzestrzeń płaszczyzny 2D ( $jasnoniebieska , rozciąga się$ ) $3D$ wektor w przestrzeni można rozłożyć na jego rzut $płaszczyzny$$odrzucenie$ i jego tej

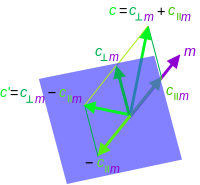
Dla dowolnego wektora $wektora$ odwracalnego ${\ displaystyle m}$ za

${\ Displaystyle a = amm ^ {- 1} = (a \ cdot m + a \ klin m)m^{-1}=a_{\|m}+a_{\perp m},}$

gdzie rzut na (lub część równoległą) jest za $displaystyle$ \ $a$

${\ Displaystyle a_ {\| m} = (a \ cdot m) m ^ {- 1}}$

a odrzucenie z $\$ lub części ortogonalnej) jest za { $displaystyle a$

${\ Displaystyle a_ {\ sprawca m} = aa_ {\| m} = (a \ klin m) m ^ {-1}.}$

Używając koncepcji $}$ jako reprezentującej podprzestrzeń i $każdy$ multiwektor ostatecznie wyrażany za pomocą wektorów, uogólnia to projekcję ogólnego multiwektora na za k $\$ displaystyle dowolny odwracalny ${\ displaystyle k}$ -blade ${\ displaystyle B}$ jak

${\ Displaystyle {\ mathcal {P}} _ {B} (A) = (A \; \ rfloor \; B ^ {-1}) \ ;\rpodłoga \;B,}$

z odrzuceniem zdefiniowanym jako

${\ Displaystyle {\ mathcal {P}} _ {B} ^ {\ sprawca} (A) = A- {\ mathcal {P}} _ {B} (A).}$

Projekcja i odrzucenie uogólniają się na ostrza zerowe ${$$}$${$ \ B ^ produkt. Wynik projekcji pokrywa się w obu przypadkach dla niezerowych ostrzy. Dla zerowych ostrzy ${\ displaystyle B}$ , należy zastosować definicję rzutu podaną tutaj, przy czym pierwszy skurcz, a nie drugi, jest na pseudoodwrotności, ponieważ tylko wtedy wynik jest koniecznie w podprzestrzeni reprezentowanej przez B {\ displaystyle $}$ . Projekcja uogólnia poprzez liniowość do ogólnych multiwektorów ${\ displaystyle A}$ . Projekcja nie jest liniowa w $B}$$displaystyle$ i nie uogólnia na obiekty które nie są ostrzami.

Odbicie

Proste odbicia w hiperpłaszczyźnie są łatwo wyrażane w algebrze poprzez koniugację z pojedynczym wektorem. Służą one do generowania grupy ogólnych odbić i obrotów .

Odbicie wektora $displaystyle$ wektora $m}$ . $m}$ tylko składnik równoległy do $displaystyle$ .

Odbicie $'}$ wzdłuż wektora lub równoważnie w hiperpłaszczyźnie prostopadłej do $displaystyle m}$$\$$jest$ samym, co zanegowanie składowej do ′ { displaystyle wektora równoległego do ${\ displaystyle m}$ . Rezultatem refleksji będzie

${\ Displaystyle c '= {-c_ {\|m} + c_ {\ perp m}} = {- (c \ cdot m) m ^ {-1} + (c \ klin m) m ^ {-1} }={(-m\cdot cm\klin c)m^{-1}}=-mcm^{-1}}$

Nie jest to najbardziej ogólna operacja, którą można uznać za odbicie, gdy wymiar ${\ displaystyle n \ geq 4}$ . Ogólne odbicie można wyrazić jako złożenie dowolnej nieparzystej liczby odbić jednoosiowych. $a' }$ można zapisać ogólne odbicie wektora za $\ displaystyle$

${\ Displaystyle a \ mapsto a' = -MaM ^ {- 1},}$

Gdzie

${\ Displaystyle M = pq \ cdots r}$ i ${\ Displaystyle M ^ {-1} = (pq \ cdots r) ^ {-1} = r ^ {-1} \ cdots q ^ {-1} p ^ {-1}.}$

Jeśli zdefiniujemy odbicie wzdłuż niezerowego wektora iloczynu $}$ jako odbicie każdego wektora w produkcie wzdłuż tego samego wektora, otrzymamy dla dowolnego iloczynu nieparzystej liczby wektorów, że m {\ displaystyle m przykład,

${\ Displaystyle (abc) '= a'b'c' = (-mama ^ {-1}) (-mbm ^ {-1}) (- mcm^{-1})=-ma(m^{-1}m)b(m^{-1}m)cm^{-1}=-mabcm^{-1}\,}$

a dla iloczynu parzystej liczby wektorów to

${\ Displaystyle (abcd) '= a'b'c'd' = (-mam ^ {-1}) (-mbm ^ {-1}) (-mcm ^ {-1}) (-mdm ^ {- 1})=mabcdm^{-1}.}$

można zapisać odbicie ogólnego multiwektora $displaystyle$ użyciu dowolnego odbicia versor $M}$

${\ Displaystyle A \ mapsto M \ alfa (A) M ^ {- 1},}$

gdzie jest automorfizmem odbicia przez początek przestrzeni wektorowej ( $rozciągnięty$$przez$ na

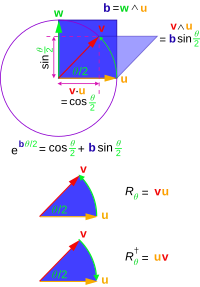
Rotacje

Wirnik, który obraca wektory w płaszczyźnie, obraca wektory o kąt $,$ czyli $}$$theta} x {\ tylda {R}} _ {\ theta$$\ displaystyle \ theta}$ to obrót o kąt ${$ . Kąt między i ${$$\ displaystyle v}$ wynosi $theta / 2}$ . $Podobne$ interpretacje obowiązują dla $multiwektora$ zamiast .

Jeśli mamy iloczyn wektorów ${\ Displaystyle R = a_ {1} a_ {2} \ cdots a_ {r}},$ oznaczamy odwrotność jako

${\ Displaystyle {\ tylda {R}} = a_ {r} \ cdots a_ {2} a_ {1}.}$

Jako przykład załóżmy, że otrzymujemy ${\ displaystyle R = ab}$

${\ Displaystyle R {\ tylda {R}} = Abba = ab ^ {2} a = a ^ {2} b ^ {2} = ba ^ {2} b = baab = {\ tylda {R}} R. }$

Skalowanie ${\ Displaystyle R}$ tak, że ${\ Displaystyle R {\ tylda {R}} = 1}$ wtedy

${\ Displaystyle (Rv {\ tylda {R}}) ^ {2} = Rv ^ {2} {\ tylda {R }}=v^{2}R{\tylda {R}}=v^{2}}$

więc ${\ tylda {R}}}$$niezmienioną$ pozostawia długość . To też możemy pokazać

${\ Displaystyle (Rv_ {1} {\ tylda {R}}) \ cdot (Rv_ {2} {\ tylda {R} })=v_{1}\cdot v_{2}}$

więc transformacja zachowuje zarówno długość $.$ Dlatego można go zidentyfikować jako obrót lub odbicie obrotowe; ${\ displaystyle R}$ nazywany jest wirnikiem , jeśli jest to właściwy obrót (jak to jest, jeśli można go wyrazić jako iloczyn parzystej liczby wektorów) i jest przykładem tego, co jest znane w GA jako versor .

$na$$obracania$ multiwektora który w płaszczyźnie iz orientacją określoną przez $displaystyle$ b {\ $}$ .

Wirniki są uogólnieniem kwaternionów na przestrzenie wymiarowe ${\ displaystyle n}$ .

Versor

ZA ${\ displaystyle k}$ -versor to multiwektor, który można wyrazić jako iloczyn geometryczny $wektorów$ . Czwartorzędy jednostkowe (pierwotnie nazywane przez Hamiltona wersorami) można identyfikować z wirnikami w przestrzeni 3D w podobny sposób, jak rzeczywiste wirniki 2D obejmują liczby zespolone; szczegóły w Dorst.

Niektórzy autorzy używają terminu „produkt versor” w odniesieniu do często występującego przypadku, gdy operand jest „wkładany” między operatorami. Przykładami takich kanapek są opisy obrotów i odbić, w tym ich morfizmy zewnętrzne. Te morfizmy zewnętrzne mają szczególnie prostą postać algebraiczną. W szczególności mapowanie wektorów postaci

${\ Displaystyle V \ do V: a \ mapsto RaR ^ {- 1}}$ rozciąga się na morfizm zewnętrzny ${\ Displaystyle {\ mathcal {G}} (V) \ do {\ mathcal {G}} (V): A \ mapsto RAR ^ {-1}.}$

Ponieważ zarówno operatory, jak i operandy są wersorami, istnieje możliwość alternatywnych przykładów, takich jak obracanie wirnika lub odbijanie spinora, zawsze pod warunkiem, że takim operacjom można przypisać pewne znaczenie geometryczne lub fizyczne.

Z twierdzenia Cartana – Dieudonnégo wynika, że ​​każdą izometrię można przedstawić jako odbicia w hiperpłaszczyznach, a ponieważ złożone odbicia zapewniają obroty, to mamy, że przekształcenia ortogonalne są wersorami.

${\ mathcal {G}} (p, q)$ kategoriach grupowych, dla prawdziwego, niezdegenerowanego, po zidentyfikowaniu grupy ${\ Displaystyle$ jako grupa wszystkich odwracalnych elementów , Lundholm podaje dowód, że „grupa $versor$${\ Displaystyle \ {v_ {1} v_ {2} \ cdots v_ {k} \ w G: v_ {i} \ w V ^ {\ razy} \}} (zbiór odwracalnych wersorów) jest$ równy Grupa Lipschitza $Clifforda$ aka grupa , chociaż Lundholm potępia to użycie).

Podgrupy Γ

Lundholm definiuje podgrupy ${\ displaystyle \ operatorname {Pin}}$ , ${\ displaystyle \ operatorname {Spin}}$ i ${\ displaystyle \ operatorname {Spin} ^ {+}}$ , generowane przez wektory jednostkowe oraz w w przypadku ${\ displaystyle$ i $\ operatorname {Spin} ^ {+}}$ może występować tylko parzysta liczba takich czynników wektorowych.

Podgrupa	Definicja	Opis
${\ displaystyle \ nazwa operatora {pin}}$	${\ Displaystyle X \ w \ Gamma: X {\ tylda {X}} = \ pm 1}$	wersety jednostek
${\ displaystyle \ nazwa operatora {spinować}}$	${\ Displaystyle {\ nazwa operatora {Pin}} \ cap {\ mathcal {G}} ^ {+}}$	nawet wersory jednostek
${\ Displaystyle \ nazwa operatora {spin} ^ {+}}$	${\ Displaystyle X \ w \ nazwa operatora {Spin}: X {\ tylda {X}} = 1}$	wirniki

Spinory definiuje się jako elementy parzystej podalgebry rzeczywistego GA; analizę podejścia GA do spinorów podają Francis i Kosowsky.

Przykłady i zastosowania

Hiperobjętość równoległoboku rozpiętego przez wektory

Dla wektorów obejmujących równoległobok mamy ${\ displaystyle a}$ i ${\ displaystyle b}$

${\ Displaystyle a \ klin b = ((a \ klin b) b ^ {- 1}) b = a_ {\ perp b} B}$

w wyniku czego $iloczyn „wysokości” i „podstawy$ równoległoboku, czyli jego pola

dowolnej $-wymiarowy$ wektorów obejmujących równoległobok ; iloczyn zewnętrzny wektorów ${\ Displaystyle a_ {1}, a_ {2}, \ ldots, a_ {n}}$ , czyli ${\ Displaystyle \ textstyle \ bigwedge _ {i = 1} ^ {n} a_ {i}}$ ma wielkość równą objętości ${\ displaystyle n}$ -równoległość. Wektor $.$ niekoniecznie ma kształt równoległoboku - jest to wygodna wizualizacja Może mieć dowolny kształt, chociaż objętość jest równa równoległościanowi.

Przecięcie prostej i płaszczyzny

Prosta L wyznaczona przez punkty T i P (których szukamy) oraz płaszczyzna wyznaczona przez dwuwektor B zawierający punkty P i Q.

Możemy zdefiniować linię parametrycznie przez ${\ Displaystyle p = t + \ alpha \ v}$ gdzie ${\ displaystyle p}$ i ${\ displaystyle t}$ są wektorami pozycji dla punktów P i T i ${\ displaystyle v}$ jest wektorem kierunku linii.

Następnie

${\ Displaystyle B \ klin (pq) = 0}$ i ${\ Displaystyle B \ klin (t + \ alfa vq) = 0}$

Więc

${\ Displaystyle \ alfa = {\ Frac {B \ klin (qt)} {B \ klin v}}}$

I

${\ Displaystyle p = t + \ lewo ({\ Frac {B \ klin (qt)} {B \ klin v}} \ prawo) v.}$

Systemy obrotowe

Matematyczny opis sił obrotowych, takich jak moment obrotowy i moment pędu , często wykorzystuje iloczyn krzyżowy rachunku wektorowego w trzech wymiarach z konwencją orientacji (ręczności).

Produkt krzyżowy w stosunku do produktu zewnętrznego. Na czerwono zaznaczono jednostkowy wektor normalny i „równoległy” dwuwektor jednostkowy.

Iloczyn krzyżowy można rozpatrywać w kategoriach iloczynu zewnętrznego, co pozwala na bardziej naturalną geometryczną interpretację iloczynu krzyżowego jako dwuwektora przy użyciu podwójnej zależności

${\ Displaystyle a \ razy b = -I (a \ klin b).}$

Na przykład moment obrotowy jest ogólnie definiowany jako wielkość składowej siły prostopadłej pomnożonej przez odległość lub pracę na kąt jednostkowy.

$, że kołowa ścieżka$$i$ dowolnej płaszczyźnie zawierająca wektory ortonormalne sparametryzowana .

${\ Displaystyle \ mathbf {r} = r ({\ kapelusz {u} }\cos \theta +{\hat {v}}\sin \theta )=r{\hat {u}}(\cos \theta +{\hat {u}}{\hat {v}}\sin \ teta )}$

Wyznaczając dwuwektor jednostkowy tej płaszczyzny jako liczbę urojoną

${\ Displaystyle {i} = {\ kapelusz {u}}} {\ kapelusz {v}} = {\ kapelusz {u}} \ klin {\ kapelusz {v}} }$

${\ Displaystyle i ^ {2} = -1}$

ten wektor ścieżki można wygodnie zapisać w złożonej postaci wykładniczej

$\ Displaystyle \ mathbf {r} = r {\ kapelusz {u}} e ^ {i \ teta}}$

a pochodna po kącie wynosi

${\ Displaystyle {\ Frac {d \ mathbf {r}} {d \ teta}} = r {\ kapelusz {u}} tj ^ {i \ teta} = \ mathbf {r} i.}$

Tak więc moment obrotowy, szybkość zmiany pracy $displaystyle$ spowodowana siłą, wynosi $F}$

${\ Displaystyle \ tau = {\ Frac {dW} {d \ teta}} = F \ cdot {\ Frac {dr} {d \ teta}} = F \ cdot (\ mathbf {r} i).}$

$w$ opisu iloczynu krzyżowego momentu obrotowego opis algebry geometrycznej nie wprowadza wektora wektor, który nie istnieje w dwóch wymiarach i który nie jest unikalny w więcej niż trzech wymiarach. Dwuwektor jednostkowy opisuje płaszczyznę i orientację obrotu, a zwrot obrotu jest względny względem kąta między wektorami ${\ Displaystyle {\ hat {u}}}$ i ${\ displaystyle {\ hat { v}}}$ .

Rachunek geometryczny

Główny artykuł: rachunek geometryczny

Rachunek geometryczny rozszerza formalizm o różniczkowanie i całkowanie, w tym geometrię różniczkową i formy różniczkowe .

Zasadniczo pochodna wektora jest zdefiniowana tak, że wersja GA twierdzenia Greena jest prawdziwa,

${\ Displaystyle \ int _ {A} dA \, \ nabla f = \ oint _ {\ częściowe A} dx \, f$

i wtedy można pisać

${\ Displaystyle \ nabla f = \ nabla \ cdot f + \ nabla \ klin f}$

jako iloczyn geometryczny, skutecznie uogólniając twierdzenie Stokesa (w tym jego wersję różniczkową).

W ${\ displaystyle 1D}$ , gdy jest $displaystyle$ z punktami końcowymi $a}$ , wtedy za {\ i ${\ displaystyle b}$

${\ Displaystyle \ int _ {A} dA \, \ nabla f = \ oint _ {\ częściowe A} dx \, f$

zmniejsza się do

${\ Displaystyle \ int _ {a} ^ {b} dx \ \$

lub fundamentalne twierdzenie rachunku całkowego.

Opracowano również koncepcję rozmaitości wektorowej i teorię integracji geometrycznej (która uogólnia formy różniczkowe).

Historia

Przed XX wiekiem

Chociaż związek geometrii z algebrą datuje się co najmniej od Elementów Euklidesa w III wieku pne ( zob . systematyczny sposób opisu geometrycznych właściwości i przekształceń przestrzeni. W tym roku Hermann Grassmann wprowadził ideę algebry geometrycznej w pełnej ogólności jako pewnego rachunku różniczkowego (analogicznego do rachunku zdań ), który zakodował wszystkie informacje geometryczne o przestrzeni. System algebraiczny Grassmanna można zastosować do wielu różnych rodzajów przestrzeni, z których głównymi są przestrzeń euklidesowa , przestrzeń afiniczna i przestrzeń rzutowa . Podążając za Grassmannem, w 1878 roku William Kingdon Clifford zbadał system algebraiczny Grassmanna obok kwaternionów Williama Rowana Hamiltona w ( Clifford 1878 ) . Z jego punktu widzenia kwaterniony opisywały pewne przekształcenia (które nazwał wirnikami ), podczas gdy algebra Grassmanna opisywała pewne właściwości (lub Streckena , takie jak długość, powierzchnia i objętość). Jego wkład polegał na zdefiniowaniu nowego iloczynu - iloczynu geometrycznego - na istniejącej algebrze Grassmanna, która realizowała kwaterniony jako żyjące w tej algebrze. Następnie Rudolf Lipschitz w 1886 roku uogólnił interpretację kwaternionów Clifforda i zastosował je do geometrii obrotów w ${\ displaystyle n}$ . Później te zmiany skłoniły innych matematyków XX wieku do sformalizowania i zbadania właściwości algebry Clifforda.

Niemniej jednak inny rewolucyjny rozwój XIX wieku całkowicie przyćmiłby algebry geometryczne: analizę wektorową , opracowaną niezależnie przez Josiaha Willarda Gibbsa i Olivera Heaviside'a . Analiza wektorowa była motywowana badaniami Jamesa Clerka Maxwella nad elektromagnetyzmem , a konkretnie potrzebą wygodnego wyrażania i manipulowania pewnymi równaniami różniczkowymi . Analiza wektorowa miała pewien intuicyjny urok w porównaniu z rygorami nowych algebr. Zarówno fizycy, jak i matematycy chętnie przyjęli go jako swój wybrany zestaw narzędzi geometrycznych, szczególnie po wpływowym podręczniku Vector Analysis z 1901 roku autorstwa Edwina Bidwella Wilsona , po wykładach Gibbsa.

Bardziej szczegółowo, istnieją trzy podejścia do algebry geometrycznej: analiza kwaternionów , zainicjowana przez Hamiltona w 1843 r. I zgeometryzowana jako wirniki przez Clifforda w 1878 r.; algebra geometryczna, zainicjowana przez Grassmanna w 1844 r.; oraz analiza wektorowa, rozwinięta z analizy czwartorzędowej pod koniec XIX wieku przez Gibbsa i Heaviside'a. Dziedzictwo analizy kwaternionów w analizie wektorowej można dostrzec w użyciu do wskazania wektorów bazowych ${\ Displaystyle \ mathbf {R} ^ {3}}$$,$${\ displaystyle j}$ k $k}$ \ : uważa się to za czysto wyimaginowane czwartorzędy. Z perspektywy algebry geometrycznej parzysta podalgebra algebry czasoprzestrzeni jest izomorficzna z GA trójwymiarowej przestrzeni euklidesowej, a kwaterniony są izomorficzne z parzystą podalgebrą GA trójwymiarowej przestrzeni euklidesowej, co łączy trzy podejścia.

XX wieku i współczesność

Postęp w badaniu algebr Clifforda po cichu postępował w XX wieku, choć w dużej mierze dzięki pracom algebraistów abstrakcyjnych , takich jak Élie Cartan , Hermann Weyl i Claude Chevalley . Geometryczne geometrycznych doczekało się wielu odrodzeń w XX wieku. W matematyce, Geometric Algebra Emila Artina omawia algebrę związaną z każdą z wielu geometrii, w tym geometrię afiniczną , geometrię rzutową , geometria symplektyczna i geometria ortogonalna . W fizyce algebry geometryczne odrodziły się jako „nowy” sposób uprawiania mechaniki klasycznej i elektromagnetyzmu, wraz z bardziej zaawansowanymi tematami, takimi jak mechanika kwantowa i teoria cechowania. David Hestenes ponownie zinterpretował macierze Pauliego i Diraca jako wektory odpowiednio w zwykłej przestrzeni i czasoprzestrzeni i był głównym współczesnym orędownikiem stosowania algebry geometrycznej.

W grafice komputerowej i robotyce odrodziły się algebry geometryczne, aby skutecznie przedstawiać obroty i inne przekształcenia. Na temat zastosowań GA w robotyce ( teoria śrub , kinematyka i dynamika z wykorzystaniem wersorów), wizji komputerowej, sterowaniu i obliczeniach neuronowych (uczenie się geometryczne) patrz Bayro (2010).

Zobacz też

• Porównanie algebry wektorów i algebry geometrycznej
• algebry Clifforda
• Algebra Grassmanna-Cayleya
• Algebra czasoprzestrzenna
• Spinor
• Kwaternion
• Algebra przestrzeni fizycznej
• Uniwersalna algebra geometryczna

Referencje i dalsze czytanie

Ułożone chronologicznie

•   Grassmann, Hermann (1844), Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert , Leipzig: O. Wigan re , OCLC 20521674
•    Artin, Emil (1988) [1957], algebra geometryczna , Wiley Classics Library, Wiley, doi : 10.1002/9781118164518 , ISBN 978-0-471-60839-4 , MR 1009557
•    Hestenes, David (1966), Algebra czasoprzestrzenna , Gordon and Breach, ISBN 978-0-677-01390-9 , OCLC 996371
•   Wheeler, JA; Misner, C.; Thorne, KS (1973), Grawitacja , WH Freeman, ISBN 978-0-7167-0344-0
•   Bourbaki, Nicolas (1980), „Rozdział 9 „Algèbres de Clifford” ”, Elementy matematyki. Algebre , Hermann, ISBN 9782225655166
•   Hestenes, Dawid ; Sobczyk, Garret (1984), Clifford Algebra to Geometric Calculus, a Unified Language for Mathematics and Physics , Springer Netherlands, ISBN 9789027716736
•   Hestenes, David (1986), JSR Chisholm; AK Commons (red.), „A Unified Language for Mathematics and Physics”, Algebry Clifforda i ich zastosowania w fizyce matematycznej , seria NATO ASI (seria C), Springer, 183 : 1–23, doi : 10.1007 / 978-94- 009-4728-3_1 , ISBN 978-94-009-4728-3
•   Doran, Chris JL (1994), Geometric Algebra and its Application to Mathematical Physics (praca doktorska), University of Cambridge , doi : 10.17863/CAM.16148 , hdl : 1810/251691 , OCLC 53604228
•   Baylis, MY, wyd. (2011) [1996], Clifford (geometryczna) algebra z zastosowaniami w fizyce, matematyce i inżynierii , Birkhäuser , ISBN 9781461241058
•   Aragonia, G.; Aragonia, JL; Rodríguez, MA (1997), „Algebry Clifforda i algebra geometryczna”, Postępy w stosowanych algebrach Clifforda , 7 (2): 91–102, doi : 10.1007 / BF03041220 , S2CID 120860757
•   Hestenes, David (1999), Nowe podstawy mechaniki klasycznej (wyd. 2), Springer Verlag, ISBN 978-0-7923-5302-7
•   Lasenby, Joan; Lasenby, Anthony N.; Doran, Chris JL (2000), „A Unified Mathematical Language for Physics and Engineering in the 21st Century” (PDF) , Philosophical Transactions of the Royal Society A , 358 (1765): 21–39, Bibcode : 2000RSPTA.358 .. .21L , doi : 10.1098/rsta.2000.0517 , S2CID 91884543 , zarchiwizowane (PDF) od oryginału w dniu 19.03.2015
•   Baylis, WE (2002), Elektrodynamika: nowoczesne podejście geometryczne (wyd. 2), Birkäuser , ISBN 978-0-8176-4025-5
•   Dorst, Leo (2002), „Wewnętrzne iloczyny algebry geometrycznej”, w Dorst, L .; Doran, C.; Lasenby, J. (red.), Zastosowania algebry geometrycznej w informatyce i inżynierii , Birkhäuser , s. 35–46, doi : 10.1007/978-1-4612-0089-5_2 , ISBN 978-1-4612-0089- 5
•   Doran, Chris JL ; Lasenby, Anthony N. (2003), Geometric Algebra for Physicists (PDF) , Cambridge University Press, ISBN 978-0-521-71595-9 , zarchiwizowane (PDF) od oryginału w dniu 2009-01-06
•   Hestenes, David (2003), „Oersted Medal Wykład 2002: Reformowanie matematycznego języka fizyki” (PDF) , Am. J. Fiz. . _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
• Hildenbrand, Dietmar; Fontijne, Daniel; Perwass, chrześcijanin; Dorst, Leo (2004), „Algebra geometryczna i jej zastosowanie w grafice komputerowej” (PDF) , Proceedings of Eurographics 2004 , doi : 10.2312/egt.20041032 , zarchiwizowane (PDF) z oryginału w dniu 06.09.2015
•   Bain, J. (2006), „Strukturalizm czasoprzestrzenny: §5 Rozmaitości a algebra geometryczna”, w: Dennis Dieks (red.), Ontologia czasoprzestrzeni , Elsevier, s. 54 i następne , ISBN 978-0-444-52768-4
•    Dorst, Leo; Fontijne, Daniel; Mann, Stephen (2007), Algebra geometryczna dla informatyki: obiektowe podejście do geometrii , Elsevier, ISBN 978-0-12-369465-2 , OCLC 132691969
•   Penrose, Roger (2007), Droga do rzeczywistości , zabytkowe książki, ISBN 978-0-679-77631-4
•   Franciszek, Mateusz R.; Kosowsky, Arthur (2008), „Budowa spinorów w algebrze geometrycznej”, Annals of Physics , 317 (2): 383–409, arXiv : math-ph / 0403040v2 , Bibcode : 2005AnPhy.317..383F , doi : 10,1016 /j.aop.2004.11.008 , S2CID 119632876
•   Li, Hongbo (2008), Algebry niezmienne i wnioskowanie geometryczne , World Scientific, ISBN 9789812770110 . Rozdział 1 w formacie PDF
•   Vince, John A. (2008), Algebra geometryczna do grafiki komputerowej , Springer, ISBN 978-1-84628-996-5
• Lundholm, Douglas; Svensson, Lars (2009), „Algebra Clifforda, algebra geometryczna i zastosowania”, arXiv : 0907,5356v1 [ matematyka-ph ]
•   Perwass, Christian (2009), Algebra geometryczna z zastosowaniami w inżynierii , geometrii i informatyce, tom. 4, Springer Science & Business Media, Bibcode : 2009gaae.book.....P , doi : 10.1007/978-3-540-89068-3 , ISBN 978-3-540-89068-3
•   Bayro-Corrochano, Eduardo (2010), Geometric Computing for Wavelet Transforms, Robot Vision, Learning, Control and Action , Springer Verlag, ISBN 9781848829299
•   Bayro-Corrochano, E.; Scheuermann, Gerik, wyd. (2010), Geometric Algebra Computing in Engineering and Computer Science , Springer, ISBN 9781849961080 Wyciąg online pod adresem http://geocalc.clas.asu.edu/html/UAFCG.html # 5 New Tools for Computational Geometry and rejuvenation of Screw Theory
•   Goldman, Ron (2010), Przemyślenie czwartorzędów: teoria i obliczenia , Morgan & Claypool, część III. Ponowne przemyślenie kwaternionów i algebr Clifforda , ISBN 978-1-60845-420-4
•   Dorst, Leo.; Lasenby, Joan (2011), Przewodnik po algebrze geometrycznej w praktyce , Springer, ISBN 9780857298119
•    Macdonald, Alan (2011), Algebra liniowa i geometryczna , CreateSpace, ISBN 9781453854938 , OCLC 704377582
•   Snygg, John (2011), Nowe podejście do geometrii różniczkowej przy użyciu algebry geometrycznej Clifforda , Springer, ISBN 978-0-8176-8282-8
•    Hildenbrand, Dietmar (2013), „Podstawy obliczeń algebry geometrycznej”, Analiza numeryczna i matematyka stosowana Icnaam 2012: Międzynarodowa konferencja analizy numerycznej i matematyki stosowanej , materiały konferencyjne AIP, 1479 (1): 27–30, Bibcode : 2012AIPC.1479 ...27H , CiteSeerX 10.1.1.364.9400 , doi : 10.1063/1.4756054 , ISBN 978-3-642-31793-4
• Bromborsky, Alan (2014), Wprowadzenie do algebry geometrycznej i rachunku różniczkowego (PDF) , zarchiwizowane (PDF) z oryginału w dniu 15.10.2019
•   Klawitter, Daniel (2014), Algebry Clifforda: modelowanie geometryczne i geometrie łańcuchów z zastosowaniem w kinematyce , Springer, ISBN 9783658076184
•   Kanatani, Kenichi (2015), Zrozumienie algebry geometrycznej: Hamilton, Grassmann i Clifford dla wizji komputerowej i grafiki , CRC Press, ISBN 9781482259513
• Li, Hongbo; Huang, Lei; Shao, Changpeng; Dong, Lei (2015), „Trójwymiarowa geometria rzutowa z algebrą geometryczną”, arXiv : 1507,06634v1 [ math.MG ]
•   Hestenes, David (11 kwietnia 2016). „Geneza algebry geometrycznej: osobista retrospektywa”. Postępy w stosowanych algebrach Clifforda . 27 (1): 351–379. doi : 10.1007/s00006-016-0664-z . S2CID 124014198 .
•   Dorst, Leo (2016), Geometria rzutowa zorientowana na 3D przez wersety ${\ Displaystyle \ mathbf {R} ^ {3,3}}$ , Springer, ISBN 9783658076184
•   Vaz, Jayme; da Rocha, Roldão (2016), Wprowadzenie do algebr i spinorów Clifforda , ISBN 978-0-19-878292-6
•   Bayro-Corrochano, Eduardo (2018). Wizja komputerowa, grafika i neurokomputery . Zastosowania algebry geometrycznej . Tom. I. Springera. ISBN 978-3-319-74830-6 .
•   Lavor, Carlile; Xambó-Descamps, Sebastià; Zaplana, Isiah (2018). Zaproszenie z algebry geometrycznej do fizyki czasoprzestrzennej, robotyki i geometrii molekularnej . Skoczek. s. 1–. ISBN 978-3-319-90665-2 .

•   Josipović, Miroslav (22 listopada 2019). Mnożenie geometryczne wektorów: wprowadzenie do algebry geometrycznej w fizyce . Springer International Publishing; Birkhauser. P. 256. ISBN 978-3-030-01756-9 .

Linki zewnętrzne

• Przegląd algebry geometrycznej i rachunku geometrycznego Alan Macdonald , Luther College, Iowa.
• Liczby urojone nie są rzeczywiste – algebra geometryczna czasoprzestrzeni . Wprowadzenie (grupa Cambridge GA).
• Geometric Algebra 2015, Masters Course in Scientific Computing , dr Chris Doran (Cambridge).
• Matematyka dla programistów gier: 5 – Metody wielowektorowe . Kompleksowe wprowadzenie i materiały referencyjne dla programistów autorstwa Iana Bella .
• Szkoła letnia IMPA 2010 Fernandes Oliveira Intro i slajdy.
• University of Fukui ESM Hitzer i Japan GA.
• Grupa Google dla GA
• Elementarz do algebry geometrycznej Wprowadzenie do GA, Jaap Suter.
• Zasoby algebry geometrycznej , której kuratorem jest Pablo Bleyer.
• Stosowane algebry geometryczne w informatyce i inżynierii 2018 Early Proceedings
• GAME2020 Mini wydarzenie algebry geometrycznej
• AGACSE 2021 Filmy

Angielskie tłumaczenia wczesnych książek i artykułów

• G. Combebiac, „rachunek tri-quaternions” (rozprawa doktorska)
• M. Markic, „Transformanty: nowy pojazd matematyczny. Synteza tri-quaternions Combebiaca i układu geometrycznego Grassmanna. The calculus of quadri-quaternions”
• C. Burali-Forti, „Metoda Grassmanna w geometrii rzutowej” Zbiór trzech notatek na temat zastosowania algebry zewnętrznej do geometrii rzutowej
• C. Burali-Forti, „Wprowadzenie do geometrii różniczkowej metodą H. Grassmanna” Wczesna książka o zastosowaniu algebry Grassmanna
• H. Grassmann, „Mechanika według zasad teorii rozciągłości” Jedna z jego prac na temat zastosowań algebry zewnętrznej.

Grupy badawcze

• Rachunek geometryczny Międzynarodowy . Linki do grup badawczych, oprogramowania i konferencji na całym świecie.
• Grupa algebry geometrycznej Cambridge . Pełnotekstowe publikacje online i inne materiały.
• Grupa Uniwersytetu Amsterdamskiego
• Badania i rozwój rachunku geometrycznego (Arizona State University).
• Archiwum blogów i biuletynów GA-Net . Nowości dotyczące rozwoju algebry geometrycznej / algebry Clifforda.
• Algebra geometryczna dla systemów działań percepcyjnych . Geometric Cybernetics Group (CINVESTAV, Campus Guadalajara, Meksyk).