Geodezja

Geodezja to nauka zajmująca się mierzeniem i przedstawianiem w trójwymiarowym , zmieniającym się w czasie geometrii , grawitacji i orientacji przestrzennej Ziemi i innych ciał astronomicznych , takich jak planety lub układy okołoplanetarne , kiedy nazywa się to geodezją planetarną .

Zjawiska geodynamiczne , w tym ruchy skorupy ziemskiej , pływy i ruchy biegunów , można badać, projektując globalne i krajowe sieci kontrolne , stosując geodezję kosmiczną i techniki geodezji naziemnej oraz opierając się na układach odniesienia i układach współrzędnych . Stanowiska pracy to geodeta i geodeta .

Nowoczesny przyrząd do pomiarów geodezyjnych z wykorzystaniem satelitów

Historia

Osobny artykuł: Historia geodezji

starożytności przednaukowej , więc samo słowo geodezja pochodzi od starożytnego greckiego słowa γεωδαισία lub geodaisia ​​(dosłownie „podział Ziemi”).

Wczesne idee dotyczące kształtu Ziemi zakładały, że Ziemia jest płaska , a niebo jest fizyczną kopułą rozciągającą się nad nią. Dwa wczesne argumenty za kulistą Ziemią były takie, że zaćmienia Księżyca wydają się obserwatorowi jako okrągłe cienie, a Gwiazda Polarna wydaje się coraz niżej na niebie podróżnikowi udającemu się na południe.

Definicja

W świecie anglojęzycznym geodezja odnosi się do nauki o mierzeniu i przedstawianiu informacji geoprzestrzennych , podczas gdy geomatyka obejmuje praktyczne zastosowania geodezji w skali lokalnej i regionalnej, w tym pomiary geodezyjne .

Geodezja w świecie niemieckojęzycznym składa się z geodezji wyższej ( Erdmessung lub höhere Geodäsie ) - zajmującej się pomiarami Ziemi w skali globalnej oraz geodezji praktycznej lub inżynierskiej ( Ingenieurgeodäsie ), która obejmuje geodezję - pomiar części lub regionów Ziemi.

Przez długi czas geodezja była nauką zajmującą się mierzeniem i rozumieniem geometrycznego kształtu Ziemi, orientacji w przestrzeni i pola grawitacyjnego; jednakże nauka i operacje geodezyjne są również stosowane do innych ciał astronomicznych w naszym Układzie Słonecznym .

Kształt Ziemi jest w dużej mierze wynikiem obrotu , który powoduje jej wybrzuszenie równikowe , oraz współzawodnictwa procesów geologicznych, takich jak zderzenie płyt , a także wulkanizmu , któremu przeciwstawia się pole grawitacyjne Ziemi. Dotyczy to powierzchni stałej, powierzchni cieczy ( dynamiczna topografia powierzchni morza ) i atmosfery ziemskiej . Z tego powodu badanie pola grawitacyjnego Ziemi nazywa się geodezją fizyczną .

Geoida i elipsoida odniesienia

Główne artykuły: geoida i elipsoida odniesienia

Geoida , przybliżenie kształtu Ziemi ; pokazano tutaj z przesadą pionową (współczynnik skalowania pionowego 10000).

Elipsoida — matematyczne przedstawienie Ziemi . Podczas mapowania we współrzędnych geodezyjnych okrąg szerokości geograficznej tworzy ścięty stożek.

Równikowy ( a ), biegunowy ( b ) i średni promień Ziemi zgodnie z definicją w Światowym Systemie Geodezyjnym z 1984 r

Geoida zasadniczo jest figurą Ziemi wyabstrahowaną z jej cech topograficznych . Jest to wyidealizowana powierzchnia równowagi wody morskiej , średnia powierzchnia poziomu morza przy braku prądów i wahań ciśnienia powietrza , i kontynuowana pod masami kontynentalnymi. W przeciwieństwie do elipsoidy odniesienia geoida jest nieregularna i zbyt skomplikowana, aby służyć jako powierzchnia obliczeniowa do rozwiązywania problemów geometrycznych, takich jak pozycjonowanie punktów. Geometryczna separacja między geoidą a elipsoidą odniesienia nazywana jest geoidą undulacją i waha się globalnie w zakresie ±110 m w oparciu o elipsoidę GRS 80.

Elipsoida odniesienia, zwykle wybrana tak, aby miała ten sam rozmiar (objętość) co geoida, jest opisana przez jej półoś wielką (promień równikowy) a i spłaszczenie f . Wielkość f = a - b / a , gdzie b jest półosią małą (promieniem biegunowym), jest czysto geometryczna. Mechaniczna eliptyczność Ziemi (spłaszczenie dynamiczne, symbol J _{2 ) może być wyznaczona z dużą precyzją poprzez obserwację} perturbacji orbity satelity . Jego związek ze spłaszczeniem geometrycznym jest pośredni i zależy od wewnętrznego rozkładu gęstości lub, mówiąc najprościej, stopnia centralnej koncentracji masy.

Geodezyjny system odniesienia z 1980 r. ( GRS 80 ), przyjęty na XVII Zgromadzeniu Ogólnym Międzynarodowej Unii Geodezji i Geofizyki ( IUGG ), przewidywał półoś wielką o długości 6 378 137 m i spłaszczenie 1: 298,257. GRS 80 zasadniczo stanowi podstawę pozycjonowania geodezyjnego przez Globalny System Pozycjonowania (GPS) i dlatego jest szeroko stosowany również poza społecznością geodezyjną. Liczne systemy używane do mapowania i tworzenia wykresów stają się przestarzałe, ponieważ kraje coraz częściej przechodzą na globalne, geocentryczne systemy odniesienia wykorzystujące elipsoidę odniesienia GRS 80.

Geoida jest „możliwą do zrealizowania” powierzchnią, co oznacza, że ​​można ją konsekwentnie zlokalizować na Ziemi za pomocą odpowiednich prostych pomiarów z obiektów fizycznych, takich jak miernik pływów . Geoidę można zatem uznać za powierzchnię fizyczną („rzeczywistą”). Elipsoida odniesienia ma jednak wiele możliwych instancji i nie jest łatwa do zrealizowania, więc jest to powierzchnia abstrakcyjna. trzeciej podstawowej powierzchni geodezyjnej — powierzchni topograficznej Ziemi.

Układy współrzędnych w przestrzeni

Główny artykuł: system geodezyjny

Dalsze informacje: Światowy System Geodezyjny

Przesunięcie punktu odniesienia między NAD27 a NAD83 w metrach.

Najwygodniej lokalizacje punktów w przestrzeni trójwymiarowej opisują trzy współrzędne kartezjańskie lub prostokątne, X , Y i Z . Od czasu pojawienia się pozycjonowania satelitarnego takie układy współrzędnych są zazwyczaj geocentryczne , z osią Z wyrównaną do (konwencjonalnej lub chwilowej) osi obrotu Ziemi.

Przed erą geodezji satelitarnej układy współrzędnych powiązane z geodezyjnym układem odniesienia próbowały być geocentryczne , ale z pochodzeniem różniącym się od geocentrum o setki metrów z powodu regionalnych odchyleń w kierunku pionu ( pion). Te regionalne geodezyjne układy odniesienia, takie jak ED 50 (europejski układ odniesienia 1950) lub NAD 27 (północnoamerykański układ odniesienia 1927), mają skojarzone z nimi elipsoidy, które są regionalnie „najlepiej dopasowane” do geoid w ich obszarach ważności, minimalizując odchylenia pionowo nad tymi obszarami.

Tylko dlatego, że satelity GPS krążą wokół geocentrum, punkt ten w naturalny sposób staje się początkiem układu współrzędnych określonego przez satelitarne środki geodezyjne, ponieważ same pozycje satelitów w przestrzeni są obliczane w takim systemie.

Geocentryczne układy współrzędnych stosowane w geodezji można naturalnie podzielić na dwie klasy:

1. Bezwładnościowe układy odniesienia, w których osie współrzędnych zachowują swoją orientację względem gwiazd stałych lub równoważnie osi obrotu idealnych żyroskopów ; oś X wskazuje równonoc wiosenną
2. Współbieżne układy odniesienia (również ECEF lub „Earth Centered, Earth Fixed”), w których osie są „przymocowane” do stałego ciała Ziemi. Oś X leży na płaszczyźnie południka obserwatorium w Greenwich .

Transformacja współrzędnych między tymi dwoma systemami z dobrym przybliżeniem jest opisana przez (pozorny) czas gwiazdowy , który odpowiada za zmiany w osiowym obrocie Ziemi ( zmiany długości dnia ). Dokładniejszy opis uwzględnia również ruch biegunowy jako zjawisko ściśle monitorowane przez geodetów.

Układy współrzędnych na płaszczyźnie

Główny artykuł: Pozycja pozioma

Siatka 2D dla współrzędnych eliptycznych

Archiwum monachijskie z płytami litograficznymi map Bawarii

W zastosowaniach geodezyjnych, takich jak geodezja i mapowanie , używane są dwa ogólne typy układów współrzędnych na płaszczyźnie:

1. Plano-biegunowy , z punktami na płaszczyźnie określonej przez ich odległość, s , od określonego punktu wzdłuż promienia mającego kierunek α od linii bazowej lub osi;
2. Prostokątny , z punktami określonymi przez odległości od dwóch wzajemnie prostopadłych osi, x i y . W przeciwieństwie do konwencji matematycznej, w praktyce geodezyjnej x wskazuje północ , a oś y wschód .

Można intuicyjnie użyć współrzędnych prostokątnych w płaszczyźnie dla swojej bieżącej lokalizacji, w którym to przypadku oś x będzie wskazywać lokalną północ. Bardziej formalnie, takie współrzędne można uzyskać ze współrzędnych 3D, stosując sztuczkę odwzorowania mapy . Niemożliwe jest odwzorowanie zakrzywionej powierzchni Ziemi na płaskiej powierzchni mapy bez deformacji. Najczęściej wybierany kompromis — zwany odwzorowaniem konforemnym — zachowuje kąty i stosunki długości, dzięki czemu małe okręgi są odwzorowywane jako małe okręgi, a małe kwadraty jako kwadraty.

Przykładem takiego odwzorowania jest UTM ( Universal Transverse Mercator ). Na płaszczyźnie mapy mamy prostokątne współrzędne x i y . W tym przypadku kierunek północny użyty jako odniesienie to mapy , a nie północ lokalna . Różnica między nimi nazywana jest zbieżnością południków .

Łatwo jest „przełożyć” między współrzędnymi biegunowymi i prostokątnymi w płaszczyźnie: niech, jak wyżej, kierunek i odległość będą odpowiednio α i s , wtedy mamy

${\ Displaystyle {\ rozpocząć {wyrównane} x & = s \ sałata \ alfa \\ y & = s \ sin \ alfa \ koniec {wyrównane}}}$

Transformacja odwrotna jest dana przez:

${\ Displaystyle {\ rozpocząć {wyrównane} s & = {\ sqrt {x ^ {2} + y ^ {2}}} \\\ alfa & = \ arctan {\ Frac {y} {x}}. \ koniec { wyrównany}}}$

Wysokości

Dalsze informacje: Pozycja pionowa i Odniesienie pionowe

Pomiar wysokości za pomocą wysokościomierza satelitarnego

wysokości punktów lub terenu są „ nad poziomem morza ” jako nieregularna, fizycznie zdefiniowana powierzchnia. Stosowane systemy wysokości to:

1. Wysokości ortometryczne
2. Wysokości dynamiczne
3. Wysokości geopotencjalne
4. Normalne wysokości

Każdy system ma swoje zalety i wady. Zarówno wysokość ortometryczna, jak i normalna są wyrażane w metrach nad poziomem morza, podczas gdy liczby geopotencjalne są miarami energii potencjalnej (jednostka: m ² s ⁻² ), a nie metrycznymi. Powierzchnią odniesienia jest geoida , powierzchnia ekwigeopotencjalna zbliżona do średniego poziomu morza, jak opisano powyżej. Dla wysokości normalnych powierzchnią odniesienia jest tzw. quasi-geoida , która ze względu na założenie gęstości w kontynuacji pod masami kontynentalnymi ma kilkumetrową odległość od geoidy.

Można powiązać te wysokości za pomocą koncepcji falowania geoidy z wysokościami elipsoidalnymi (znanymi również jako wysokości geodezyjne ), reprezentującymi wysokość punktu powyżej elipsoidy odniesienia . Satelitarne odbiorniki pozycjonowania zazwyczaj zapewniają wysokości elipsoidalne, chyba że są wyposażone w specjalne oprogramowanie do konwersji oparte na modelu geoidy.

Układy odniesienia geodezyjne

Główny artykuł: transformacja układu odniesienia

Ponieważ współrzędne i wysokości punktów geodezyjnych zawsze uzyskuje się w systemie, który sam został skonstruowany na podstawie obserwacji w świecie rzeczywistym, geodeci wprowadzili koncepcję „geodezyjnego układu odniesienia” (liczba mnoga punktów odniesienia): fizyczna (rzeczywista) realizacja współrzędnej system używany do opisu lokalizacji punktów. Ta realizacja wynika z wyboru (a więc konwencjonalnych) wartości współrzędnych dla jednego lub więcej punktów odniesienia. W przypadku danych wysokościowych wystarczy wybrać jeden punkt odniesienia — reper referencyjny, zazwyczaj pływomierz na brzegu. Tak więc mamy pionowe układy odniesienia, takie jak NAVD 88 (North American Vertical Datum 1988), NAP ( Normaal Amsterdams Peil ), układ Kronsztadu, układ Triestu i wiele innych.

Zarówno w matematyce, jak i geodezji układ współrzędnych jest „układem współrzędnych” zgodnie z terminologią ISO , podczas gdy International Earth Rotation and Reference Systems Service (IERS) używa terminu „układ odniesienia” na to samo. Kiedy współrzędne są realizowane poprzez wybór punktów odniesienia i ustalenie geodezyjnego odniesienia, ISO mówi o „systemie odniesienia za pomocą współrzędnych”, podczas gdy IERS używa do tego samego „układu odniesienia”. Termin ISO dla transformacji punktu odniesienia to ponownie „transformacja współrzędnych”.

Pozycjonowanie

Zobacz też: Sieć geodezyjna § Techniki pomiarowe

GPS Block IIA orbituje nad Ziemią

Wstępna akwizycja sygnału GPS w 2D

Geopozycjonowanie lub po prostu pozycjonowanie to określanie położenia określonego przez zestaw współrzędnych geodezyjnych punktu na lądzie, morzu lub w przestrzeni w układzie współrzędnych (pozycjonowanie punktowe) lub względem innego punktu (pozycjonowanie względne ). Położenie punktu w przestrzeni oblicza się na podstawie pomiarów łączących ziemskie lub pozaziemskie punkty o znanym położeniu („znane punkty”) z ziemskimi punktami o nieznanym położeniu („nieznane punkty”). Obliczenia mogą obejmować przekształcenia między astronomicznymi i ziemskimi układami współrzędnych lub między nimi. Znanymi punktami używanymi do pozycjonowania punktów mogą być GNSS lub punkty triangulacyjne sieci wyższego rzędu.

Tradycyjnie geodeci budowali hierarchię sieci, aby umożliwić pozycjonowanie punktów w kraju. Najwyżej w tej hierarchii znajdowały się sieci triangulacyjne, zagęszczone w sieci trawersów ( wielokątów ), w które wplecione są lokalne pomiary kartograficzne i geodezyjne, zwykle zbierane za pomocą taśmy mierniczej, graniastosłupa narożnego i biało-czerwonych tyczek.

Obecnie powszechnie stosowany jest GPS, z wyjątkiem pomiarów specjalistycznych (np. w inżynierii podziemnej lub inżynierii precyzyjnej). Sieci wyższego rzędu są mierzone za pomocą statycznego GPS , przy użyciu pomiaru różnicowego do określenia wektorów między punktami naziemnymi. Wektory te są następnie dostosowywane w tradycyjny sposób sieciowy. Globalny wielościan stale działających stacji GPS pod auspicjami IERS jest podstawą do zdefiniowania pojedynczego globalnego, geocentrycznego układu odniesienia, który służy jako odniesienie „zerowego rzędu” (globalne), do którego dołączane są pomiary krajowe.

Pozycjonowanie kinematyczne w czasie rzeczywistym (RTK GPS) jest często stosowane w mapowaniu geodezyjnym . W tej technice pomiarowej nieznane punkty mogą zostać szybko powiązane z pobliskimi znanymi punktami ziemskimi.

Jednym z celów pozycjonowania punktów jest zapewnienie znanych punktów do pomiarów mapowania, zwanych również kontrolą (poziomą i pionową). W kraju mogą istnieć tysiące takich geodezyjnie określonych punktów, zwykle udokumentowanych przez krajowe agencje kartograficzne. Geodeci zajmujący się nieruchomościami i ubezpieczeniami wykorzystają je do powiązania swoich lokalnych pomiarów.

Problemy geodezyjne

Główny artykuł: Geodezja na elipsoidzie § Rozwiązanie problemów bezpośrednich i odwrotnych

Znak kontroli geodezyjnej

nawigacyjne , program Apollo

W geodezji geometrycznej istnieją dwa główne problemy:

Pierwsze ( bezpośrednie lub do przodu ) zadanie geodezyjne

Mając podane współrzędne punktu oraz kierunek ( azymut ) i odległość do drugiego punktu, wyznacz współrzędne tego drugiego punktu.

Drugi ( odwrotny lub odwrotny ) problem geodezyjny

Mając współrzędne dwóch punktów, wyznacz azymut i długość linii (prostej, krzywej lub geodezyjnej ) łączącej te punkty.

Rozwiązania obu problemów w geometrii płaszczyzny sprowadzają się do prostej trygonometrii i są ważne dla małych obszarów na powierzchni Ziemi; na kuli rozwiązania stają się znacznie bardziej złożone, ponieważ na przykład w problemie odwrotnym azymuty różnią się między dwoma punktami końcowymi wzdłuż łuku łączącego wielkiego koła .

Ogólne rozwiązanie nazywa się geodezyjnym dla rozważanej powierzchni, a równania różniczkowe dla geodezyjnego są rozwiązywalne numerycznie. Na elipsoidzie obrotowej geodezję można wyrazić za pomocą całek eliptycznych, które są zwykle oceniane w kategoriach rozwinięcia szeregu — patrz na przykład wzory Vincenty'ego .

Koncepcje obserwacyjne

Pochylenie osiowe (lub nachylenie ), oś obrotu, płaszczyzna orbity , równik niebieski i ekliptyka . Ziemia jest pokazana widziana ze Słońca ; kierunek orbity jest przeciwny do ruchu wskazówek zegara (w lewo).

globalnej anomalii grawitacyjnej nad oceanami z GRACE NASA (Gravity Recovery And Climate Experiment)

Zgodnie z definicją geodezji (a także astronomii ), niektóre podstawowe pojęcia obserwacyjne, takie jak kąty i współrzędne, obejmują (najczęściej z punktu widzenia lokalnego obserwatora):

• Pion lub pion : (linia wzdłuż) kierunek lokalnej grawitacji.
• Zenit : (kierunek do) przecięcia wektora grawitacji skierowanego w górę w punkcie i sfery niebieskiej .
• Nadir : (kierunek do) punktu antypodalnego, w którym skierowany w dół wektor grawitacji przecina (przesłoniętą) sferę niebieską.
• Horyzont niebieski : płaszczyzna prostopadła do wektora grawitacji w punkcie.
• Azymut : kąt kierunkowy w płaszczyźnie horyzontu, zwykle liczony zgodnie z ruchem wskazówek zegara od północy (w geodezji i astronomii) lub południa (we Francji).
• Wysokość : wysokość kątowa obiektu nad horyzontem; alternatywnie: odległość zenitalna równa 90 stopni minus elewacja.
• Lokalne współrzędne topocentryczne : azymut (kąt kierunku w płaszczyźnie horyzontu), kąt elewacji (lub kąt zenitu), odległość.
• Północny biegun niebieski : przedłużenie chwilowej osi obrotu Ziemi ( precesyjnej i nutacyjnej ) rozciągającej się na północ w celu przecięcia sfery niebieskiej. (Podobnie dla południowego bieguna niebieskiego).
• Równik niebieski : (chwilowe) przecięcie płaszczyzny równikowej Ziemi ze sferą niebieską.
• Płaszczyzna południka : każda płaszczyzna prostopadła do równika niebieskiego i zawierająca bieguny niebieskie.
• Południk lokalny : płaszczyzna zawierająca kierunek do zenitu i bieguna niebieskiego.

Pomiary

Dalsze informacje: Geodezja satelitarna , Astronomia geodezyjna , Geodezja , Grawimetria i niwelacja

Wariacje w polu grawitacyjnym Księżyca , z NASA

Urządzenia do pomiaru grawitacji, wahadło (po lewej) i grawimetr absolutny (po prawej)

Grawimetr względny

Powierzchnia odniesienia (poziom) używana do określania różnic wysokości i systemów odniesienia wysokości jest znana jako średni poziom morza . Tradycyjna poziomica bezpośrednio daje takie (najbardziej użyteczne ze względów praktycznych) wysokości nad poziomem morza ; bardziej ekonomiczne wykorzystanie przyrządów GPS do wyznaczania wysokości wymaga dokładnej znajomości figury geoidy , ponieważ GPS podaje wysokości tylko powyżej elipsoidy odniesienia GRS80 . Wraz z poprawą wyznaczania geoidy można spodziewać się wzrostu wykorzystania GPS do wyznaczania wysokości.

Teodolit jest przyrządem służącym do pomiaru kątów poziomych i pionowych (względem lokalnego pionu) względem punktów docelowych . Ponadto tachymetr określa elektronicznie lub elektrooptycznie odległość do celu i jest wysoce zautomatyzowany, a nawet robotyczny w operacjach. Szeroko stosowana w tym samym celu jest metoda swobodnego pozycjonowania stacji.

Zwykle do lokalnych badań szczegółowych stosuje się tachymetry, chociaż staromodna technika prostokątna wykorzystująca pryzmat kątowy i taśmę stalową jest nadal niedrogą alternatywą. Jak wspomniano, istnieją również szybkie i stosunkowo dokładne kinematyczne techniki GPS w czasie rzeczywistym (RTK). Zebrane dane są znakowane i rejestrowane cyfrowo w celu wprowadzenia ich do Systemu Informacji Geograficznej (GIS).

Geodezyjne odbiorniki GNSS (najczęściej GPS ) generują bezpośrednio współrzędne 3D w układzie współrzędnych geocentrycznych . Jedną z takich ram jest WGS84 , a także ramy Międzynarodowej Służby Systemów Obrotu Ziemi i Odniesienia ( IERS ). Odbiorniki GNSS prawie całkowicie zastąpiły instrumenty naziemne w badaniach sieci bazowych na dużą skalę.

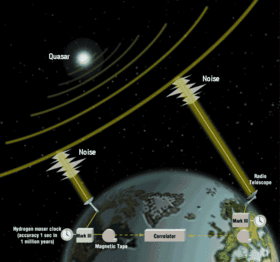
Do monitorowania nieregularności obrotu Ziemi i ruchów tektonicznych płyt oraz do badań geodezyjnych obejmujących całą planetę, metody interferometrii o bardzo długiej linii bazowej (VLBI) mierzące odległości do kwazarów , lunar laser range (LLR) mierzący odległości do pryzmatów na Księżycu i satelity stosuje się laserowy pomiar odległości (SLR) do pomiaru odległości do pryzmatów na sztucznych satelitach .

Grawitację mierzy się za pomocą grawimetrów , których są dwa rodzaje. Pierwsze to grawimetry absolutne , oparte na pomiarze przyspieszenia swobodnego spadku (np. odbijającego pryzmatu w rurze próżniowej ). Służą do ustalenia pionowej kontroli geoprzestrzennej lub w terenie. Po drugie, grawimetry względne są oparte na sprężynach i są bardziej powszechne. Stosowane są w pomiarach grawitacyjnych na dużych obszarach — w celu ustalenia kształtu geoidy na tych obszarach. Najdokładniejsze grawimetry względne nazywane są grawimetrami nadprzewodzącymi , które są czułe na jedną tysięczną jednej miliardowej grawimetru powierzchniowego. Na całym świecie używa się dwudziestu kilku grawimetrów nadprzewodzących do badania pływów, rotacji Ziemi , ładunków wewnętrznych , oceanicznych i atmosferycznych, jak również w weryfikacji newtonowskiej stałej grawitacji .

W przyszłości grawitacja i wysokość mogą stać się mierzalne przy użyciu szczególnej relatywistycznej koncepcji dylatacji czasu , mierzonej za pomocą zegarów optycznych .

Jednostki i miary na elipsoidzie

Dalsze informacje: Współrzędne geodezyjne

Definicja szerokości geograficznej (φ) i długości geograficznej (λ) na elipsoidzie obrotowej (lub kuli). Odległość między siatkami wynosi 10 stopni. Szerokość geograficzna jest definiowana jako kąt między normalną do elipsoidy a płaszczyzną równika.

Szerokość i długość geograficzna podawana jest w stopniach, minutach łuku i sekundach łuku. Są to kąty , a nie miary metryczne i opisują kierunek lokalnej normalnej do odniesienia elipsoidy obrotowej. Kierunek ten jest w przybliżeniu taki sam jak kierunek pionu, tj. lokalna grawitacja, która jest również normalna do powierzchni geoidy. Z tego powodu wyznaczanie pozycji astronomicznej – mierzenie kierunku pionu za pomocą środków astronomicznych – działa dość dobrze, gdy używa się również elipsoidalnego modelu kształtu Ziemi.

Jedna mila geograficzna, zdefiniowana jako jedna minuta łuku na równiku, równa się 1855,32571922 m. Jedna mila morska to jedna minuta szerokości geograficznej astronomicznej. Promień krzywizny elipsoidy zmienia się wraz z szerokością geograficzną i jest najdłuższy na biegunie, a najkrótszy na równiku, tak samo jak w przypadku mili morskiej.

w obecnych definicjach różni się o 200 ppm) . Ta sytuacja oznacza, że ​​jeden kilometr to mniej więcej (1/40 000) * 360 * 60 południkowych minut kątowych, czyli 0,54 mili morskiej. (Zauważ, że nie jest to dokładnie tak, ponieważ te dwie jednostki zostały zdefiniowane na różnych podstawach, więc międzynarodowa mila morska wynosi dokładnie 1852 m, co odpowiada zaokrągleniu 1000/0,54 m do czterech cyfr).

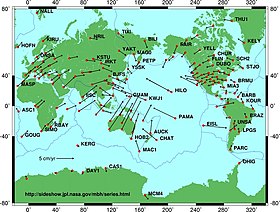
Zmiany czasowe

Zobacz także: Geoida § Zmiana czasowa

Globalny ruch tektoniczny płyt za pomocą GPS

Jak działa interferometria o bardzo długiej linii bazowej (VLBI).

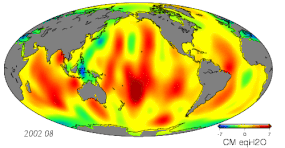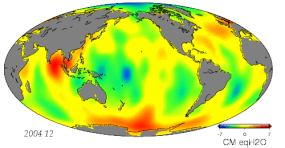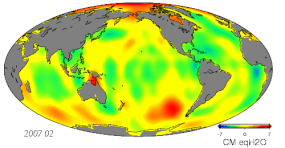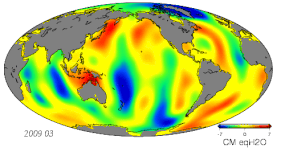
W geodezji stosuje się różne techniki do badania zmieniających się w czasie powierzchni, ciał masowych, pól fizycznych i układów dynamicznych. Punkty na powierzchni Ziemi zmieniają swoje położenie w wyniku różnych mechanizmów:

• Ruch płyt kontynentalnych, tektonika płyt
• Epizodyczny ruch pochodzenia tektonicznego, szczególnie w pobliżu linii uskoków
• Okresowe skutki spowodowane pływami i obciążeniem pływowym
• Polodowcowe wypiętrzenie terenu w wyniku dostosowania izostatycznego
• Wahania masy spowodowane zmianami hydrologicznymi, w tym atmosferą, kriosferą, hydrologią lądową i oceanami
• Sub-dzienny ruch biegunowy
• Zmienność długości dnia
• Zmiany środka masy Ziemi (geocentrum).
• Ruchy antropogeniczne, takie jak budowa zbiorników lub wydobycie ropy naftowej lub wody

Kierownik projektu NASA opowiada o swojej pracy w projekcie Space Geodesy Project, w tym przegląd jego czterech podstawowych technik: GPS, VLBI , LLR / SLR i DORIS .

Geodynamika to dyscyplina zajmująca się badaniem deformacji i ruchów skorupy ziemskiej oraz jej solidności jako całości. Często powyższa definicja obejmuje badanie nieregularnego obrotu Ziemi. Badania geodynamiczne wymagają ziemskich układów odniesienia realizowanych przez stacje należące do Global Geodetic Observing System (GGOS).

Techniki badania zjawisk geodynamicznych w skali globalnej obejmują:

• Pozycjonowanie satelitarne przez GPS , GLONASS , Galileo i BeiDou
• Interferometria o bardzo długiej linii bazowej (VLBI)
• Satelitarny zasięg laserowy (SLR) i księżycowy zasięg laserowy (LLR)
• DORIS
• Niwelacja dokładna regionalnie i lokalnie
• Precyzyjne tachymetry
• Monitorowanie zmian grawitacji za pomocą grawimetrii lądowej, powietrznej, morskiej i kosmicznej
• Wysokościomierz satelitarny oparty na obserwacjach mikrofalowych i laserowych do badania powierzchni oceanów, wzrostu poziomu mórz i monitorowania pokrywy lodowej
• Interferometryczny radar z syntetyczną aperturą (InSAR) wykorzystujący zdjęcia satelitarne.

Znani geodeci

Główny artykuł: Lista geodetów

Zobacz też: Znani geodeci

Zobacz też

Kategoria główna: Geodezja

• Nauka o systemach Ziemi - Naukowe badanie sfer Ziemi i ich naturalnych zintegrowanych systemów
• Lista geodetów – Znani geodeci
• Historia geofizyki
• Geodynamika – nauka o dynamice Ziemi
• Planetary science - Nauka o planetach i układach planetarnych

Podstawy

• Pojęcia i techniki we współczesnej geografii
• Geodezja na elipsoidzie
• Historia geodezji
• Geodezja fizyczna
• Obwód Ziemi
• Fizyka
• Nauki o Ziemi

Agencje rządowe

• Krajowa agencja kartograficzna
• Narodowe badanie geodezyjne Stanów Zjednoczonych
• Narodowa Agencja Wywiadu Geoprzestrzennego
• Badanie uzbrojenia
• Wybrzeża Stanów Zjednoczonych i badanie geodezyjne
• Służba Geologiczna Stanów Zjednoczonych

Organizacje międzynarodowe

• Międzynarodowa Unia Geodezji i Geofizyki (IUGG)
• Międzynarodowe Stowarzyszenie Geodezji (IAG)
• Międzynarodowa Federacja Geodetów (IFS)
• Międzynarodowa Organizacja Studentów Geodezji (IGSO)

Inny

• Zbiór danych parametrów geodezyjnych EPSG
• Łuk południka
• Geodezja

Dalsza lektura

• FR Helmert, Matematyczne i fizyczne teorie wyższej geodezji , część 1 , ACIC (St. Louis, 1964). To jest angielskie tłumaczenie Die mathematischen und physikalischen Theorieen der höheren Geodäsie , tom 1 (Teubner, Lipsk, 1880).
• FR Helmert, Matematyczne i fizyczne teorie wyższej geodezji , część 2 , ACIC (St. Louis, 1964). To jest angielskie tłumaczenie Die mathematischen und physikalischen Theorieen der höheren Geodäsie , tom 2 (Teubner, Lipsk, 1884).
• B. Hofmann-Wellenhof i H. Moritz, Physical Geodesy , Springer-Verlag Wien, 2005. (Ten tekst jest zaktualizowanym wydaniem klasyka z 1967 r. autorstwa WA Heiskanena i H. Moritza).
• W. Kaula, Theory of Satellite Geodesy: Applications of Satellites to Geodesy , Dover Publications, 2000. (Ten tekst jest przedrukiem klasyka z 1966 roku).
• Vaníček P. i EJ Krakiwsky, Geodesy: the Concepts , s. 714, Elsevier, 1986.
•   Torge, W (2001), Geodezja (3. wydanie), opublikowane przez de Gruyter, ISBN 3-11-017072-8 .
• Thomas H. Meyer, Daniel R. Roman i David B. Zilkoski. „Co wzrost ?” (Jest to seria czterech artykułów opublikowanych w Surveying and Land Information Science, SaLIS ).
  • „Część I: Wprowadzenie” SaLIS Cz. 64, nr 4, strony 223–233, grudzień 2004.
  • „Część II: Fizyka i grawitacja” SaLIS Cz. 65, nr 1, strony 5–15, marzec 2005.
  • „Część III: Systemy wysokościowe” SaLIS Cz. 66, nr 2, strony 149–160, czerwiec 2006.
  • „Część IV: Wysokość GPS” SaLIS Cz. 66, nr 3, strony 165–183, wrzesień 2006.

Linki zewnętrzne

Geodezja w Wikibooks Media związane z geodezją w Wikimedia Commons

• Wytyczne dotyczące świadomości geodezyjnej, Podkomitet ds. Geodezji, Komitet ds. Geomatyki, Międzynarodowe Stowarzyszenie Producentów Ropy i Gazu
• „Geodezja” . Encyklopedia Britannica . Tom. 11 (wyd. 11). 1911. s. 607–615.