Dylatacja czasu

Ten artykuł dotyczy koncepcji fizycznej. Aby zapoznać się z terminem używanym w psychologii, zobacz Percepcja czasu .

Dylatacja czasu wyjaśnia, dlaczego dwa pracujące zegary będą podawać różne czasy po różnych przyspieszeniach. Na przykład czas płynie wolniej na ISS , opóźniając się o około 0,01 sekundy na każde upływające 12 ziemskich miesięcy. Aby GPS działały, muszą dostosować się do podobnego zakrzywienia czasoprzestrzeni, aby prawidłowo koordynować z systemami na Ziemi.

W fizyce i teorii względności dylatacja czasu to różnica w czasie , który upłynął , mierzony przez dwa zegary . Jest to spowodowane albo względną prędkością między nimi ( specjalne relatywistyczne „kinetyczne” dylatacja czasu), albo różnicą potencjału grawitacyjnego między ich lokalizacjami ( ogólna relatywistyczna grawitacyjna dylatacja czasu ). Gdy nie jest określony, „dylatacja czasu” zwykle odnosi się do efektu spowodowanego prędkością.

Po skompensowaniu różnych opóźnień sygnału spowodowanych zmieniającą się odległością między obserwatorem a poruszającym się zegarem (tj. efektem Dopplera ), obserwator zmierzy, że poruszający się zegar będzie tykał wolniej niż zegar, który jest w spoczynku we własnym układzie odniesienia obserwatora . Ponadto zegar, który znajduje się blisko masywnego ciała (a zatem ma niższy potencjał grawitacyjny) będzie rejestrował mniej czasu, który upłynął niż zegar znajdujący się dalej od wspomnianego masywnego ciała (i który ma wyższy potencjał grawitacyjny).

Te przewidywania teorii względności zostały wielokrotnie potwierdzone eksperymentalnie i mają praktyczne znaczenie, na przykład w działaniu systemów nawigacji satelitarnej, takich jak GPS i Galileo . Dylatacja czasu była również tematem prac science fiction.

Historia

Osobny artykuł: Historia szczególnej teorii względności

Dylatacja czasu przez czynnik Lorentza była przewidziana przez kilku autorów na przełomie XIX i XX wieku. Joseph Larmor (1897), przynajmniej dla elektronów krążących wokół jądra, napisał: „... poszczególne elektrony opisują odpowiednie części swoich orbit w czasach krótszych dla układu [reszty] w stosunku: 1 - v ${ \sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$ ". Emil Cohn (1904) konkretnie powiązał ten wzór z szybkością zegarów. W kontekście szczególnej teorii względności pokazał to m.in Alberta Einsteina (1905), że efekt ten dotyczy samej natury czasu, a także jako pierwszy zwrócił uwagę na jego wzajemność lub symetrię. Następnie Hermann Minkowski (1907) wprowadził pojęcie czasu właściwego , które dodatkowo wyjaśniło znaczenie dylatacji czasu.

Dylatacja czasu spowodowana prędkością względną

Z lokalnego układu odniesienia niebieskiego zegara, czerwony zegar będąc w ruchu postrzegany jest jako tykający wolniej.

Szczególna teoria względności wskazuje, że dla obserwatora w inercjalnym układzie odniesienia zegar poruszający się względem niego będzie tykał wolniej niż zegar znajdujący się w spoczynku w jego układzie odniesienia. Ten przypadek jest czasami nazywany specjalnym relatywistycznym dylatacją czasu. Im większa prędkość względna , tym większe jest między sobą dylatacja czasu, przy czym czas zwalnia aż do zatrzymania, gdy zbliżamy się do prędkości światła (299 792 458 m/s).

Teoretycznie dylatacja czasu umożliwiłaby pasażerom szybko poruszającego się pojazdu przemieszczanie się dalej w przyszłość w krótkim czasie. Przy odpowiednio wysokich prędkościach efekt jest dramatyczny. Na przykład jeden rok podróży może odpowiadać dziesięciu latom na Ziemi. Rzeczywiście, stałe przyspieszenie 1 g pozwoliłoby ludziom podróżować przez cały znany Wszechświat w ciągu jednego ludzkiego życia.

Jednak przy obecnej technologii poważnie ograniczającej prędkość podróży kosmicznych różnice odczuwane w praktyce są znikome: po 6 miesiącach na Międzynarodowej Stacji Kosmicznej ( ISS), krążącej wokół Ziemi z prędkością około 7700 m/s, astronauta postarzałby się około 0,005 sekundy mniej niż na Ziemi. Kosmonauci Siergiej Krikalow i Siergiej Awdiejew doświadczyli dylatacji czasu o około 20 milisekund w porównaniu z czasem, który upłynął na Ziemi.

Proste wnioskowanie

Po lewej : Obserwator w spoczynku mierzy czas 2 L / c między kolokalnymi zdarzeniami generowania sygnału świetlnego w A i dotarciem do A. Po prawej : Zdarzenia według obserwatora poruszającego się na lewo od układu: dolne lustro A, gdy sygnał jest generowany w czas t'= 0, górne zwierciadło B gdy sygnał zostanie odbity w czasie t'=D/c , dolne zwierciadło A gdy sygnał powraca w czasie t'=2D/c

Dylatację czasu można wywnioskować z zaobserwowanej stałości prędkości światła we wszystkich układach odniesienia, podyktowanej drugim postulatem szczególnej teorii względności .

Ta stałość prędkości światła oznacza, że ​​wbrew intuicji prędkości obiektów materialnych i światła nie sumują się. Nie można sprawić, by prędkość światła wydawała się większa, przesuwając się w kierunku lub od źródła światła.

Rozważmy więc prosty pionowy zegar składający się z dwóch luster A i B , pomiędzy którymi odbija się impuls świetlny. Odległość między lustrami wynosi L , a zegar tyka raz za każdym razem, gdy impuls światła uderza w lustro A.

W klatce, w której zegar jest w spoczynku (patrz lewa część diagramu), impuls świetlny wytycza ścieżkę o długości 2 L , a okres zegara wynosi 2 L podzielone przez prędkość światła:

${\ Displaystyle \ Delta t = {\ Frac {2L} {c}}}$

Z układu odniesienia poruszającego się obserwatora poruszającego się z prędkością v względem układu spoczynkowego zegara (prawa część wykresu) impuls świetlny jest widziany jako śledzący dłuższą, zakrzywioną ścieżkę. Utrzymanie stałej prędkości światła dla wszystkich obserwatorów inercjalnych wymaga wydłużenia okresu tego zegara z perspektywy poruszającego się obserwatora. Oznacza to, że mierząc w ramce poruszającej się względem lokalnego zegara, zegar ten będzie działał wolniej. Proste zastosowanie twierdzenia Pitagorasa prowadzi do dobrze znanego przewidywania szczególnej teorii względności:

Całkowity czas, w którym impuls światła prześledził swoją drogę, jest określony wzorem:

${\ Displaystyle \ delta t '= {\ Frac {2D} {c}}}$

Długość pół drogi można obliczyć jako funkcję znanych wielkości jako:

${\ Displaystyle D = {\ sqrt {\ lewo ({\ Frac {1} {2}} v \ Delta t '\ prawo) ^ {2} + L ^{2}}}}$

Eliminacja zmiennych D i L z tych trzech równań skutkuje:

${\ Displaystyle \ Delta t '= {\ Frac {\ Delta t} {\ sqrt {1- {\ Frac {v ^ {2}} {c ^ {2} }}}}}}$

$,$ że okres zegara poruszającego się obserwatora $jest$ dłuższy niż okres w samego

Ponieważ wszystkie zegary, które mają wspólny okres w układzie spoczynkowym, powinny mieć wspólny okres, gdy są obserwowane z układu ruchomego, wszystkie inne zegary — mechaniczne, elektroniczne, optyczne (takie jak identyczna pozioma wersja zegara w przykładzie) — powinny wykazywać takie same zależne od prędkości dylatacje czasu.

Wzajemność

Czas UV zegara w S jest krótszy w porównaniu do Ux′ w S′, a czas UW zegara w S′ jest krótszy w porównaniu do Ux w S

Poprzeczna dylatacja czasu. Niebieskie kropki reprezentują impuls światła. Każda para kropek, pomiędzy którymi „odbija się” światło, to zegar. W ramce każdej grupy zegarów mierzono, że druga grupa tyka wolniej, ponieważ impuls świetlny poruszającego się zegara musi pokonać większą odległość niż impuls świetlny zegara stacjonarnego. Tak jest, mimo że zegary są identyczne, a ich względny ruch jest doskonale odwrotny.

Biorąc pod uwagę pewien układ odniesienia i opisanego wcześniej „nieruchomego” obserwatora, gdyby drugi obserwator towarzyszył „poruszającemu się” zegarowi, każdy z obserwatorów postrzegałby zegar drugiego jako tykający wolniej niż jego własny zegar lokalny, ze względu na obaj postrzegają drugiego jako tego, który jest w ruchu względem ich własnego stacjonarnego układu odniesienia.

Zdrowy rozsądek podpowiadałby, że jeśli upływ czasu zwolnił dla poruszającego się obiektu, obiekt ten zaobserwowałby odpowiednie przyspieszenie czasu w świecie zewnętrznym. Wbrew intuicji szczególna teoria względności przewiduje coś przeciwnego. Kiedy dwóch obserwatorów porusza się względem siebie, każdy zmierzy spowolnienie zegara drugiego, zgodnie z ruchem względem układu odniesienia obserwatora.

Chociaż wydaje się to wewnętrznie sprzeczne, podobna osobliwość występuje w życiu codziennym. Jeśli dwie osoby A i B obserwują się z daleka, B wyda się A małe, ale jednocześnie A będzie małe B. Znając efekty perspektywy, nie ma w tej sytuacji sprzeczności ani paradoksu .

Wzajemność zjawiska prowadzi również do tzw. paradoksu bliźniąt , w którym porównuje się starzenie się bliźniąt, jednego przebywającego na Ziemi, a drugiego wyruszającego w podróż kosmiczną, i gdzie wzajemność sugeruje, że obie osoby powinny być w tym samym wieku, kiedy ponownie połączyć. Wręcz przeciwnie, pod koniec podróży w obie strony podróżujący bliźniak będzie młodszy niż rodzeństwo na Ziemi. Dylemat, jaki rodzi paradoks, można jednak wytłumaczyć faktem, że podróżujący bliźniak musi wyraźnie przyspieszyć w co najmniej trzech fazach podróży (początek, zmiana kierunku i koniec), podczas gdy drugi doświadczy jedynie znikomego przyspieszenia, ze względu na do obrotu i obrotu Ziemi. Podczas faz przyspieszania podróży kosmicznych dylatacja czasu nie jest symetryczna.

Testy eksperymentalne

Zobacz też: Testy szczególnej teorii względności

efekt Dopplera

Główny artykuł: eksperyment Ivesa – Stilwella

• Deklarowanym przez Ivesa i Stilwella (1938, 1941) celem tych eksperymentów było zweryfikowanie efektu dylatacji czasu, przewidywanego przez teorię eteru Larmora-Lorentza, w wyniku ruchu w eterze przy użyciu sugestii Einsteina, że ​​​​efekt Dopplera w promieniach kanałowych zapewni odpowiednie eksperyment. Eksperymenty te mierzyły przesunięcie Dopplera promieniowania emitowanego z promieni katodowych , patrząc bezpośrednio z przodu i bezpośrednio z tyłu. Wykryte wysokie i niskie częstotliwości nie były klasycznie przewidywanymi wartościami:
  $${\ Displaystyle {\ Frac {f_ {0}} {1-v / c}} \ qquad {\ tekst {i}} \ qquad {\ Frac {f_ { 0}}{1+v/c}}}$$
  Wysokie i niskie częstotliwości promieniowania z ruchomych źródeł mierzono jako:
  $${\ Displaystyle {\ sqrt {\ Frac {1 + v/c} {1-v/c}}} f_ {0} = \ gamma \ lewo (1 + v/c \ prawo) f_ {0} \ qquad { \text{and}}\qquad {\sqrt {\frac {1-v/c}{1+v/c}}}f_{0}=\gamma \left(1-v/c\right)f_{ 0}\,}$$
  jak wydedukował Einstein (1905) z transformacji Lorentza , gdy źródło działa wolno przez czynnik Lorentza.
• Hasselkamp, ​​Mondry i Scharmann (1979) zmierzyli przesunięcie Dopplera od źródła poruszającego się pod kątem prostym do linii wzroku. Najbardziej ogólny związek między częstotliwościami promieniowania z ruchomych źródeł jest określony wzorem:
  $$_ {\ operatorname {wykryto}} = f _ {\ operatorname {reszta } }{\left(1-{\frac {v}{c}}\cos \phi \right)/{\sqrt {1-{v^{2}}/{c^{2}}}}} }$$
  jak wydedukował Einstein (1905). Dla φ = 90° ( cos φ = 0 ) zmniejsza się to do f _wykryte = f _reszta γ . Ta niższa częstotliwość z poruszającego się źródła może być przypisana efektowi dylatacji czasu i jest często nazywana poprzecznym efektem Dopplera i została przewidziana przez teorię względności.
• W 2010 roku zaobserwowano dylatację czasu przy prędkościach mniejszych niż 10 metrów na sekundę przy użyciu optycznych zegarów atomowych połączonych światłowodem o długości 75 metrów.

Poruszające się cząstki

Główny artykuł: Eksperymentalne testowanie dylatacji czasu

• porównanie czasów życia mionów przy różnych prędkościach. W laboratorium wytwarzane są powolne miony; a do atmosfery bardzo szybko poruszające się miony są wprowadzane przez promieniowanie kosmiczne. Przyjmując czas życia mionu w spoczynku jako wartość laboratoryjną 2,197 μs, czas życia mionu wytwarzanego przez promieniowanie kosmiczne poruszającego się z prędkością 98% prędkości światła jest około pięć razy dłuższy, zgodnie z obserwacjami. Przykładem są Rossi i Hall (1941), którzy porównali populację mionów wytwarzanych przez promieniowanie kosmiczne na szczycie góry z populacją obserwowaną na poziomie morza.
• Czas życia cząstek wytwarzanych w akceleratorach cząstek jest dłuższy ze względu na dylatację czasu. W takich eksperymentach „zegarem” jest czas procesów prowadzących do rozpadu mionu, a procesy te zachodzą w poruszającym się mionie z jego własnym „taktem zegarowym”, czyli znacznie wolniejszym niż zegar laboratoryjny. Jest to rutynowo brane pod uwagę w fizyce cząstek elementarnych i przeprowadzono wiele dedykowanych pomiarów. Na przykład w pierścieniu magazynującym miony w CERN stwierdzono, że czas życia mionów krążących z γ = 29,327 jest wydłużony do 64,378 μs, co potwierdza dylatację czasu z dokładnością do 0,9 ± 0,4 części na tysiąc.

Czas własny i diagram Minkowskiego

Diagram Minkowskiego i paradoks bliźniaków

Zegar C w ruchu względnym między dwoma zsynchronizowanymi zegarami A i B. C spotyka A ​​w d i B w f .

Paradoks bliźniaczy . Jeden bliźniak musi zmieniać ramy, co prowadzi do różnych właściwych czasów w liniach świata bliźniaka.

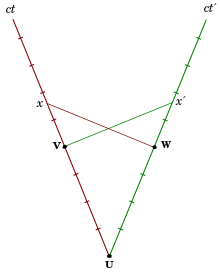
Na diagramie Minkowskiego z pierwszego obrazu po prawej zegar C spoczywający w układzie inercjalnym S ′ spotyka zegar A w punkcie di zegar B w punkcie f (oba spoczywają w S). Wszystkie trzy zegary jednocześnie zaczynają tykać w S. Linia świata A jest osią ct, linia świata B przecinająca f jest równoległa do osi ct, a linia świata C jest osią ct'. Wszystkie zdarzenia równoczesne z d w S są na osi x, w S′ na osi x′.

Właściwy czas między dwoma wydarzeniami wskazuje zegar obecny na obu wydarzeniach. Jest niezmienny, tj. we wszystkich układach inercjalnych uzgodniono, że ten czas jest wskazywany przez ten zegar. Odstęp df jest więc czasem właściwym zegara C i jest krótszy względem czasów współrzędnych ef=dg zegarów B i A w S. I odwrotnie, również czas właściwy ef B jest krótszy względem czasu, jeśli w S ′, ponieważ zdarzenie e zostało zmierzone w S′ już w czasie i ze względu na względność równoczesności, na długo przed tym, jak C zaczęło tykać.

Z tego widać, że właściwy czas między dwoma zdarzeniami wskazywany przez nieprzyśpieszony zegar obecny przy obu zdarzeniach, w porównaniu z zsynchronizowanym czasem współrzędnych mierzonym we wszystkich innych układach inercjalnych, jest zawsze minimalnym odstępem czasu między tymi zdarzeniami . Jednak odstęp między dwoma zdarzeniami może również odpowiadać właściwemu czasowi przyspieszonych zegarów obecnych w obu zdarzeniach. We wszystkich możliwych czasach właściwych między dwoma zdarzeniami, czas właściwy zegara bez przyspieszenia jest maksymalny , co jest rozwiązaniem paradoksu bliźniaków .

Wyprowadzenie i sformułowanie

Współczynnik Lorentza jako funkcja prędkości (w jednostkach naturalnych, gdzie c = 1). Zauważ, że dla małych prędkości (poniżej 0,1) γ wynosi około 1.

Oprócz zastosowanego powyżej zegara świetlnego, wzór na dylatację czasu można bardziej ogólnie wyprowadzić z czasowej części transformacji Lorentza . Niech będą dwa zdarzenia, w których poruszający się zegar wskazuje , więc: $\ displaystyle t_ {a}}$ i ${\ displaystyle t_ {b}}$

${\ Displaystyle t_ {a} ^ {\ pierwsza} = {\frac {t_{a}-{\frac {vx_{a}}{c^{2}}}}{\sqrt {1-{\frac {v^{2}}{c^{2}} }}}},\ t_{b}^{\prime }={\frac {t_{b}-{\frac {vx_{b}}{c^{2}}}}{\sqrt {1-{ \frac {v^{2}}{c^{2}}}}}}}$

Ponieważ zegar pozostaje w spoczynku w swoim układzie inercjalnym, wynika $displaystyle$$b$ t jest dana wzorem:

${\ Displaystyle \ Delta t '= \ gamma \, \ Delta t = {\ Frac {\ Delta t} {\ sqrt {1- {\ Frac { v^{2}}{c^{2}}}}}}\,}$

gdzie Δ t to odstęp czasu między dwoma zdarzeniami kolokalnymi (tj . zachodzącymi w tym samym miejscu) dla obserwatora w pewnym układzie inercjalnym ( np . te same zdarzenia, zmierzone przez innego obserwatora, poruszające się bezwładnie z prędkością v względem poprzedniego obserwatora, v to prędkość względna między obserwatorem a poruszającym się zegarem, c to prędkość światła, a współczynnik Lorentza (konwencjonalnie oznaczane grecką literą gamma lub γ) to:

${\ Displaystyle \ gamma = {\ Frac {1} {\ sqrt {1 - {\ Frac {v ^ {2}} {c ^ {2}}}}}} \, }$

W ten sposób stwierdzono, że czas trwania cyklu zegara poruszającego się zegara jest zwiększony: mierzy się, że „działa wolno”. Zakres takich wariancji w zwykłym życiu, gdzie v ≪ c , nawet biorąc pod uwagę podróże kosmiczne, nie jest wystarczająco duży, aby wywołać łatwo wykrywalne efekty dylatacji czasu, a takie znikomo małe efekty można bezpiecznie zignorować w większości celów. Dopiero gdy obiekt zbliża się do prędkości rzędu 30 000 km/s (1/10 prędkości światła), dylatacja czasu staje się ważna.

Ruch hiperboliczny

Główny artykuł: ruch hiperboliczny (teoria względności)

W szczególnej teorii względności dylatacja czasu jest najprościej opisana w warunkach, w których prędkość względna jest niezmienna. Niemniej jednak równania Lorentza pozwalają obliczyć właściwy czas i ruch w przestrzeni dla prostego przypadku statku kosmicznego, który jest przykładany z siłą na jednostkę masy względem jakiegoś obiektu odniesienia w ruchu jednostajnym (tj. ze stałą prędkością), równą g przez cały czas okres pomiaru.

₀ Niech t będzie czasem w układzie inercjalnym, zwanym później układem spoczynkowym. Niech x będzie współrzędną przestrzenną, a kierunek stałego przyspieszenia i prędkość statku kosmicznego (względem ramy spoczynkowej) niech będą równoległe do osi x . Zakładając, że pozycja statku kosmicznego w czasie t = 0 wynosi x = 0 , a prędkość v i definiujemy następujący skrót:

${\ Displaystyle \ gamma _ {0} = {\ Frac {1} {\ sqrt {1-v_ {0} ^ {2} / c ^ {2}}}}}$

obowiązują następujące formuły:

Pozycja:

${\ Displaystyle x (t) = {\ Frac {c ^ {2}} {g}} \ lewo ({{ \sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}-\gamma _{0}\ Prawidłowy)}$

Prędkość:

${\ Displaystyle v (t) = {\ Frac {gt + v_ {0} \ gamma _ {0}} {\ sqrt {1+{\frac {\left(gt+v_{0}\gamma _{0}\right)^{2}}{c^{2}}}}}}}$

Czas właściwy jako funkcja czasu współrzędnych:

${\ Displaystyle \ tau (t) = \ tau _ {0} + \ int _ {0} ^ {t} \sqrt {1-\left({\frac {v(t')}{c}}\right)^{2}}}dt'}$

₀₀ W przypadku, gdy v (0) = v = 0 i τ (0) = τ = 0 całkę można wyrazić jako funkcję logarytmiczną lub równoważnie jako odwrotną funkcję hiperboliczną :

${\ Displaystyle \ tau (t) = {\ Frac {c} {g }}\ln \left({\frac {gt}{c}}+{\sqrt {1+\left({\frac {gt}{c}}\right)^{2}}}\right)= {\frac {c}{g}}\operatorname {arsinh} \left({\frac {gt}{c}}\right)}$

Jako funkcje właściwego czasu statku obowiązują następujące wzory: ${\ displaystyle \ tau}$

Pozycja:

${\ Displaystyle x (\ tau) = {\ Frac {c ^ {2}} {g}} \ lewo (\ cosh {\ Frac {g \tau }{c}}-1\prawo)}$

Prędkość:

${\ Displaystyle v (\ tau) = c \ tanh {\ Frac {g \ tau} {c}}}$

Czas koordynacyjny jako funkcja czasu właściwego:

${\ Displaystyle t (\ tau) = {\ Frac {c} {g}} \ sinh {\ Frac {g \ tau} {c}}}$

Hipoteza zegara

Hipoteza zegara polega na założeniu, że tempo, w jakim zegar podlega dylatacji czasu, nie zależy od jego przyspieszenia, a jedynie od jego prędkości chwilowej. Jest to równoznaczne ze stwierdzeniem, że zegar poruszający się po ścieżce mierzy właściwy czas , określony przez: ${\ displaystyle P}$

${\ Displaystyle \ tau = \ int _ {P} {\ sqrt {dt ^ {2} - dx^{2}/c^{2}-dy^{2}/c^{2}-dz^{2}/c^{2}}}}$

Hipoteza zegara została pośrednio (ale nie wprost) zawarta w oryginalnym sformułowaniu szczególnej teorii względności Einsteina z 1905 roku. Od tego czasu stało się to standardowym założeniem i jest zwykle zaliczane do aksjomatów szczególnej teorii względności, zwłaszcza w świetle eksperymentalnej weryfikacji aż do bardzo dużych przyspieszeń w akceleratorach cząstek .

Dylatacja czasu spowodowana grawitacją lub przyspieszeniem

Główny artykuł: Dylatacja czasu grawitacyjnego

Czas płynie szybciej dalej od środka ciężkości, co widać w przypadku masywnych obiektów (takich jak Ziemia)

Dylatacja czasu grawitacyjnego jest doświadczana przez obserwatora, który na pewnej wysokości w studni potencjału grawitacyjnego stwierdza, że ​​​​jego lokalne zegary mierzą mniej czasu, który upłynął niż identyczne zegary znajdujące się na większej wysokości (a zatem mające wyższy potencjał grawitacyjny).

Grawitacyjna dylatacja czasu ma znaczenie np. dla astronautów ISS. Podczas gdy względna prędkość astronautów spowalnia ich czas, zmniejszony wpływ grawitacji w ich lokalizacji przyspiesza go, choć w mniejszym stopniu. Poza tym czas wspinacza teoretycznie upływa nieco szybciej na szczycie góry niż u ludzi na poziomie morza. Obliczono również, że z powodu dylatacji czasu jądro Ziemi jest o 2,5 roku młodsze od skorupy . „Zegar używany do odmierzania czasu pełnego obrotu Ziemi zmierzy, że dzień będzie dłuższy o około 10 ns dziennie na każdy kilometr wysokości nad geoidą odniesienia”. Podróż do regionów przestrzeni, w których zachodzi ekstremalne grawitacyjne dylatowanie czasu, na przykład w pobliżu (ale nie poza horyzontem zdarzeń ) czarnej dziury , może przynieść wyniki przesunięcia w czasie, analogiczne do tych z podróży kosmicznych z prędkością bliską prędkości światła.

W przeciwieństwie do dylatacji czasu prędkości, w której obaj obserwatorzy mierzą drugiego jako wolniejszego starzenia się (efekt odwrotności), grawitacyjna dylatacja czasu nie jest odwrotna. Oznacza to, że przy dylatacji czasu grawitacyjnego obaj obserwatorzy zgadzają się, że zegar znajdujący się bliżej środka pola grawitacyjnego ma wolniejsze tempo i zgadzają się co do stosunku różnicy.

Testy eksperymentalne

Główny artykuł: Eksperymentalne testowanie dylatacji czasu

• W 1959 roku Robert Pound i Glen A. Rebka zmierzyli bardzo niewielkie grawitacyjne przesunięcie ku czerwieni w częstotliwości światła emitowanego na niższych wysokościach, gdzie pole grawitacyjne Ziemi jest stosunkowo bardziej intensywne. Wyniki mieściły się w granicach 10% przewidywań ogólnej teorii względności. W 1964 roku Pound i JL Snider zmierzyli wynik w granicach 1% wartości przewidywanej przez grawitacyjną dylatację czasu. (Patrz eksperyment Pounda-Rebki )
• W 2010 roku zmierzono dylatację czasu grawitacyjnego na powierzchni Ziemi przy różnicy wysokości wynoszącej zaledwie jeden metr za pomocą optycznych zegarów atomowych.

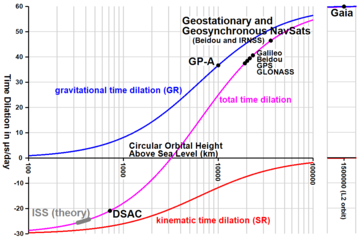
Połączony efekt dylatacji czasu i prędkości grawitacyjnej

Dylatacja czasu dziennego (zysk lub strata, jeśli jest ujemna) w mikrosekundach jako funkcja (kołowego) promienia orbity r = rs / re , gdzie rs to promień orbity satelity, a re to promień równika Ziemi, obliczony przy użyciu metryki Schwarzschilda. Przy r ≈ 1,497 nie ma dylatacji czasu. Tutaj skutki ruchu i zmniejszonej grawitacji znoszą się. Astronauci ISS latają poniżej, podczas gdy satelity GPS i geostacjonarne latają powyżej.

Dylatacja czasu dziennego na wysokości orbity kołowej z podziałem na składowe

Pomiar czasu o wysokiej dokładności, śledzenie satelitarne na niskiej orbicie okołoziemskiej i pomiar czasu pulsarów to zastosowania, które wymagają uwzględnienia połączonych efektów masy i ruchu w tworzeniu dylatacji czasu. Praktyczne przykłady obejmują międzynarodowy standard czasu atomowego i jego związek ze standardem barycentrycznego czasu współrzędnych używanym dla obiektów międzyplanetarnych.

Relatywistyczne efekty dylatacji czasu dla Układu Słonecznego i Ziemi można bardzo dokładnie modelować za pomocą rozwiązania równań pola Einsteina Schwarzschilda . W metryce Schwarzschilda przedział jest określony wzorem: ${\ text {E}}}$

${\ Displaystyle dt _ {\ tekst {E}} ^ {2} = \ lewo (1- {\ Frac {2GM_ {\ tekst {i}}} {r_ {\ tekst {i}} c ^ {2}}} \right)dt_{\text{c}}^{2}-\left(1-{\frac {2GM_{\text{i}}}{r_{\text{i}}c^{2}}} \right)^{-1}{\frac {dx^{2}+dy^{2}+dz^{2}}{c^{2}}}}$

Gdzie:

• ${\ Displaystyle dt_ {\ tekst {E}}}$ to mały przyrost czasu właściwego (interwał, który można zarejestrować na zegarze atomowym), ${\ displaystyle t _ {\ tekst {E}}}$
• ${\ Displaystyle dt_ {\ tekst {c}}}$ to mały przyrost współrzędnej ${\ Displaystyle t _ {\ tekst {c}}}$ ( czas współrzędnych ),
• ${\ Displaystyle dx, dy, dz}$ to małe przyrosty w trzech współrzędnych pozycji zegara ${\ Displaystyle x, y, z}$
• ${\ Displaystyle {\ Frac {-GM_ {i}}} {r_ {i}}}}$ reprezentuje sumę newtonowskich potencjałów grawitacyjnych związanych z masami w sąsiedztwie, na podstawie ich odległości ${ \displaystyle r_{i}}$ z zegara. Suma ta obejmuje wszelkie potencjały pływowe.

Współrzędna prędkości zegara jest dana wzorem:

${\ Displaystyle v ^ {2} = {\ Frac {dx ^ {2} + dy ^ {2} + dz ^ {2}} { dt_{\text{c}}^{2}}}}$

Czas współrzędnych $czas$ , który można by odczytać na hipotetycznym „zegarze współrzędnych” znajdującym się nieskończenie daleko od wszystkich mas grawitacyjnych $stacjonarnym$ w układ współrzędnych ( ${\ displaystyle v = 0}$ ). Dokładna zależność między szybkością czasu właściwego a szybkością współrzędnych czasu dla zegara z radialną składową prędkości jest następująca:

${\ Displaystyle {\ Frac {dt _ {\ tekst {E}}} {dt _ {\ tekst {c}}}} = {\ sqrt {1 + {\ Frac {2U} {c ^ {2} }}-{\frac {v^{2}}{c^{2}}}+\left({\frac {c^{2}}{2U}}+1\right)^{-1}{ \frac {{v_{\shortparallel}}^{2}}{c^{2}}}}}={\sqrt {1-\left(\beta ^{2}+\beta _{e}^{ 2}+{\frac {\beta _{\shortparallel}^{2}\beta _{e}^{2}}{1-\beta _{e}^{2}}}\right)}}}$

Gdzie:

• ${\ Displaystyle v _ {\ shortparallel}}$ to prędkość radialna,
• ${\ Displaystyle v_ {e} = {\ sqrt {\ Frac {2GM_ {i}}} {r_ {i}}}}}$ to prędkość ucieczki,
• ${\ Displaystyle \ beta = v/c}$ , ${\ Displaystyle \ beta _ {e} = v_ {e} / c}$ i ${\ displaystyle \beta _{\shortparallel }=v_{\shortparallel }/c}$ to prędkości wyrażone jako procent prędkości światła c ,
• $_$ _ stąd $się$ połowie kwadratu prędkości ucieczki

Powyższe równanie jest dokładne przy założeniach rozwiązania Schwarzschilda. Redukuje się do równania dylatacji czasu prędkości w obecności ruchu i braku grawitacji, tj. ${\ Displaystyle \ beta _ {e} = 0}$ . Redukuje się do grawitacyjnego równania dylatacji czasu przy braku ruchu i obecności grawitacji, tj. ${\ Displaystyle \ beta = 0 = \ beta _ {\ shortparallel}}$ .

Testy eksperymentalne

• Hafele i Keating w 1971 roku latali samolotami pasażerskimi z cezowymi zegarami atomowymi na wschód i zachód wokół Ziemi, aby porównać upływający czas z zegarem, który pozostał w Obserwatorium Marynarki Wojennej Stanów Zjednoczonych . W grę weszły dwa przeciwstawne efekty. Oczekiwano, że zegary starzeją się szybciej (pokazują większy czas, który upłynął) niż zegar odniesienia, ponieważ przez większość podróży znajdowały się w wyższym (słabszym) potencjale grawitacyjnym (por. eksperyment Pounda- Rebki ). Ale także, przeciwnie, spodziewano się, że poruszające się zegary starzeją się wolniej ze względu na prędkość ich ruchu. Na podstawie rzeczywistych torów lotu każdej podróży teoria przewidywała, że ​​​​latające zegary, w porównaniu z zegarami referencyjnymi w Obserwatorium Marynarki Wojennej Stanów Zjednoczonych, powinny stracić 40 ± 23 nanosekund podczas podróży na wschód i zyskać 275 ± 21 nanosekund podczas podróży na zachód . W stosunku do atomowej skali czasu Obserwatorium Marynarki Wojennej Stanów Zjednoczonych latające zegary straciły 59 ± 10 nanosekund podczas podróży na wschód i zyskały 273 ± 7 nanosekund podczas podróży na zachód (gdzie słupki błędów reprezentują odchylenie standardowe). W 2005 roku Narodowe Laboratorium Fizyczne w Wielkiej Brytanii zgłosili ograniczoną replikację tego eksperymentu. Eksperyment NPL różnił się od oryginału tym, że zegary cezowe zostały wysłane w krótszą podróż (Londyn – Waszyngton, powrót DC), ale zegary były dokładniejsze. Zgłoszone wyniki mieszczą się w granicach 4% przewidywań teorii względności, w granicach niepewności pomiarów.
• Globalny system pozycjonowania można uznać za eksperyment działający w sposób ciągły, zarówno w szczególnej, jak i ogólnej teorii względności. Zegary na orbicie są korygowane zarówno pod kątem specjalnych, jak i ogólnych relatywistycznych efektów dylatacji czasu, jak opisano powyżej , tak że (jak obserwuje się z powierzchni Ziemi) działają z taką samą szybkością jak zegary na powierzchni Ziemi.

W kulturze popularnej

Prędkość i grawitacyjna dylatacja czasu były tematem prac science fiction w różnych mediach. Niektóre przykłady w filmie to filmy Interstellar i Planet of the Apes . W Interstellar kluczowym punktem fabuły jest planeta, która znajduje się blisko obracającej się czarnej dziury i na której powierzchni jedna godzina odpowiada siedmiu latom na Ziemi ze względu na dylatację czasu. Fizyk Kip Thorne współpracował przy tworzeniu filmu i wyjaśnił jego naukowe koncepcje w książce The Science of Interstellar .

Dylatacja czasu została wykorzystana w odcinkach Doctor Who World Enough i Time oraz The Doctor Falls , które mają miejsce na statku kosmicznym w pobliżu czarnej dziury. Ze względu na ogromne przyciąganie grawitacyjne czarnej dziury i długość statku (400 mil), czas płynie szybciej na jednym końcu niż na drugim. Kiedy towarzysz Doktora, Bill, zostaje zabrany na drugi koniec statku, ona czeka latami, aż ją uratuje; w jego czasach mijają tylko minuty. Co więcej, rozszerzenie pozwala Cybermenom ewoluować w „szybszym” tempie niż wcześniej obserwowano w serialu.

Tau Zero , powieść Poula Andersona , jest wczesnym przykładem koncepcji w literaturze science fiction. W powieści statek kosmiczny wykorzystuje silnik strumieniowy Bussarda do przyspieszenia do wystarczająco wysokich prędkości, aby załoga spędziła na pokładzie pięć lat, ale na Ziemi mijają trzydzieści trzy lata, zanim dotrą do celu. Dylatacja prędkości w czasie została wyjaśniona przez Andersona za pomocą współczynnika tau która maleje coraz bliżej zera, gdy statek zbliża się do prędkości światła - stąd tytuł powieści. Z powodu wypadku załoga nie jest w stanie zatrzymać przyspieszania statku kosmicznego, powodując tak ekstremalne wydłużenie czasu, że załoga doświadcza Wielkiego Kryzysu na końcu wszechświata. Inne przykłady w literaturze, takie jak Rocannon's World i The Forever War , podobnie wykorzystują relatywistyczne dylatacje czasu jako naukowo wiarygodne narzędzie literackie, dzięki któremu niektóre postacie starzeją się wolniej niż reszta wszechświata.

Zobacz też

• Skurcz długości
• Masa w szczególnej teorii względności

Dalsza lektura

•   Callender, C .; Edney, R. (2001). Przedstawiamy czas . Książki z ikonami . ISBN 978-1-84046-592-1 .
• Einstein, A. (1905). „Zur Elektrodynamik bewegter Körper” . Annalen der Physik . 322 (10): 891. Bibcode : 1905AnP...322..891E . doi : 10.1002/andp.19053221004 .
• Einstein, A. (1907). „Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips” . Annalen der Physik . 328 (6): 197–198. Bibcode : 1907AnP...328..197E . doi : 10.1002/andp.19073280613 .
•   Hasselkamp, ​​D.; Mondry, E.; Scharmann, A. (1979). „Bezpośrednia obserwacja poprzecznego przesunięcia Dopplera”. Zeitschrift für Physik A. 289 (2): 151–155. Bibcode : 1979ZPhyA.289..151H . doi : 10.1007/BF01435932 . S2CID 120963034 .
• Ives, ON; Stilwell GR (1938). „Eksperymentalne badanie tempa poruszającego się zegara”. Journal of Optical Society of America . 28 (7): 215–226. Bibcode : 1938JOSA...28..215I . doi : 10.1364/JOSA.28.000215 .
• Ives, ON; Stilwell, GR (1941). „Eksperymentalne badanie tempa poruszającego się zegara. II”. Journal of Optical Society of America . 31 (5): 369–374. Bibcode : 1941JOSA...31..369I . doi : 10.1364/JOSA.31.000369 .
• Joos, G. (1959). "Bewegte Bezugssysteme in der Akustik. Der Doppler-Effekt". Lehrbuch der Theoretischen Physik, Zweites Buch (wyd. 11).
• Larmor, J. (1897). „O dynamicznej teorii ośrodka elektrycznego i świecącego” . Transakcje filozoficzne Towarzystwa Królewskiego . 190 : 205–300. Bibcode : 1897RSPTA.190..205L . doi : 10.1098/rsta.1897.0020 . (trzeci i ostatni z serii artykułów o tej samej nazwie).
• Poincare, H. (1900). „La théorie de Lorentz et le principe de Réaction”. Archiwa Néerlandaises . 5 : 253–78.
•   Puri, A. (2015). „Einstein kontra prosta formuła wahadła: czy grawitacja spowalnia wszystkie zegary?”. Edukacja fizyczna . 50 (4): 431. Bibcode : 2015PhyEd..50..431P . doi : 10.1088/0031-9120/50/4/431 . S2CID 118217730 .
• Reinhardt S.; i in. (2007). „Test relatywistycznej dylatacji czasu z szybkimi optycznymi zegarami atomowymi przy różnych prędkościach” (PDF) . Fizyka przyrody . 3 (12): 861–864. Bibcode : 2007NatPh...3..861R . doi : 10.1038/nphys778 . Zarchiwizowane od oryginału (PDF) w dniu 12.07.2009.
• Rossi, B.; Hall, DB (1941). „Zmiana tempa rozpadu mezotronów z pędem”. Przegląd fizyczny . 59 (3): 223. Bibcode : 1941PhRv...59..223R . doi : 10.1103/PhysRev.59.223 .
• Weiss, M. „Dwukierunkowy transfer czasu dla satelitów” . Narodowy Instytut Norm i Technologii . Zarchiwizowane od oryginału w dniu 2017-05-29.
• Voigt, W. (1887). „Zasada Über das Dopplera”. Nachrichten von der Königlicher Gesellschaft der Wissenschaften zu Göttingen . 2 : 41–51.

Linki zewnętrzne

• Merrifield, Michael. „Czynnik Lorentza (i dylatacja czasu)” . Sześćdziesiąt symboli . Brady Haran z Uniwersytetu w Nottingham .