Ruch hiperboliczny (teoria względności)

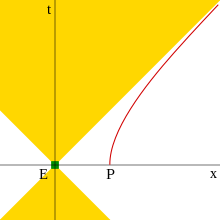
Ruch hiperboliczny można zwizualizować na diagramie Minkowskiego, na którym ruch przyspieszającej cząstki odbywa się wzdłuż osi ${\ displaystyle X}$ . Każda $\ eta = \ alpha \ tau$ zdefiniowana przez $η =$ Displaystyle z ${\ Displaystyle c = 1, \ alfa = 1}$ ) w równaniu ( 2 ).

Ruch hiperboliczny to ruch obiektu ze stałym przyspieszeniem właściwym w szczególnej teorii względności . Nazywa się to ruchem hiperbolicznym, ponieważ równanie opisujące ścieżkę obiektu w czasoprzestrzeni jest hiperbolą , co można zobaczyć na wykresie na diagramie Minkowskiego , którego współrzędne reprezentują odpowiedni układ bezwładności (bez przyspieszenia). Ten ruch ma kilka interesujących cech, między innymi to, że możliwe jest wyprzedzenie fotonu, jeśli ma się wystarczającą przewagę, jak można wywnioskować z diagramu.

Historia

Hermann Minkowski (1908) wykazał zależność między punktem na linii świata a wielkością czterokrotnego przyspieszenia i „hiperboli krzywizny” ( niem . Krümmungshyperbel ). W kontekście sztywności Borna , Max Born (1909) ukuł następnie termin „ruch hiperboliczny” ( niem . Hyperbelbewegung ) dla przypadku stałej wielkości przyspieszenia czterokrotnego, a następnie przedstawił szczegółowy opis cząstki w ruchu hiperbolicznym i wprowadził odpowiedni „hiperbolicznie przyspieszony układ odniesienia” ( niem . hyperbolisch beschleunigtes Bezugsystem ). Formuły Borna zostały uproszczone i rozszerzone przez Arnolda Sommerfelda (1910). Wczesne recenzje można znaleźć w podręcznikach Maxa von Laue (1911, 1921) lub Wolfganga Pauliego (1921). Zobacz także Galeriu (2015) lub Gourgoulhon (2013) oraz Przyspieszenie (szczególna teoria względności)#Historia .

Linia świata

Właściwe przyspieszenie cząstki definiuje się jako przyspieszenie , które cząstka „odczuwa”, gdy przyspiesza z jednego $inercyjnego$ układu odniesienia drugiego. Jeśli przyspieszenie właściwe jest skierowane równolegle do linii ruchu, jest to związane ze zwykłym trzykrotnym przyspieszeniem w szczególnej teorii względności przez ${\ Displaystyle a = du/dT}$

${\ Displaystyle \ alpha = \ gamma ^ {3} a = {\ Frac {1} {\ lewo (1- u^{2}/c^{2}\right)^{3/2}}}{\frac {du}{dT}},}$

gdzie $jest$$współrzędnych$$,$ cząstki współczynnikiem $Lorentza$ , jest prędkością światła i . Rozwiązanie równania ruchu daje pożądane wzory, które można wyrazić za pomocą czasu współrzędnych, a także czasu własnego $displaystyle \$$}$ . Dla uproszczenia wszystkie początkowe wartości czasu, położenia i prędkości można ustawić na 0, a zatem:

${\ Displaystyle {\ rozpocząć {tablica} {c | c} {\ rozpocząć {wyrównane} u (T) & = {\ Frac {\ alfa T} {\ sqrt {1 + \ lewo ({\ Frac {\ alfa T }{c}}\right)^{2}}}}\\&=c\tanh \left(\operatorname {arsinh} {\frac {\alpha T}{c}}\right)\\X(T )&={\frac {c^{2}}{\alpha}}\left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}} }-1\right)\\&={\frac {c^{2}}{\alpha }}\left(\cosh \left(\operatorname {arsinh} {\frac {\alpha T}{c}} \right)-1\right)\\c\tau (T)&={\frac {c^{2}}{\alpha }}\ln \left({\sqrt {1+\left({\frac {\alpha T}{c}}\right)^{2}}}+{\frac {\alpha T}{c}}\right)\\&={\frac {c^{2}}{\ alpha }}\operatorname {arsinh} {\frac {\alpha T}{c}}\end{aligned}}&{\begin{aligned}u(\tau)&=c\tanh {\frac {\alpha \ tau }{c}}\\\\X(\tau )&={\frac {c^{2}}{\alpha}}\left(\cosh {\frac {\alpha \tau}{c}} -1\right)\\\\cT(\tau )&={\frac {c^{2}}{\alpha}}\sinh {\frac {\alpha \tau}{c}}\\\\ \\\end{wyrównane}}\end{tablica}}}$

 

 

 

 

()

$} T ^ {2} = c ^ {4}/\ alfa ^ {2}}$${\ Displaystyle \ lewo (X + c ^ {2} / \ alfa \ prawo) ^ {2} -c ^ {$ 2 , która jest hiperbolą w czasie T i zmienną lokalizacji przestrzennej ${\ displaystyle X}$ . W tym przypadku przyspieszony obiekt znajduje się w czasie ${\ displaystyle T = 0}$${\ displaystyle T = 0}$ . Jeśli zamiast tego istnieją wartości początkowe różne od zera, wzory na ruch hiperboliczny przyjmują postać:

${\ Displaystyle {\ scriptstyle {\ rozpocząć {tablica} {c | c} {\ rozpocząć {wyrównane} u (T) & = {\ Frac {u_ {0} \ gamma _ {0} + \ alfa T} {\ sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)^{2}}}}\quad \\&=c\tanh \ left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right\}\\X(T)&=X_ {0}+{\frac {c^{2}}{\alpha}}\left({\sqrt {1+\left({\frac {u_{0}\gamma _{0}+\alpha T} {c}}\right)^{2}}}-\gamma _{0}\right)\\&=X_{0}+{\frac {c^{2}}{\alpha }}\left\ {\cosh \left[\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)\right]-\gamma _{0} \right\}\\c\tau (T)&=c\tau _{0}+{\frac {c^{2}}{\alpha }}\ln \left({\frac {{\sqrt { c^{2}+\left(u_{0}\gamma_{0}+\alpha T\right){}^{2}}}+u_{0}\gamma _{0}+\alpha T} {\left(c+u_{0}\right)\gamma _{0}}}\right)\\&=c\tau_{0}+{\frac {c^{2}}{\alpha} }\left\{\operatorname {arsinh} \left({\frac {u_{0}\gamma _{0}+\alpha T}{c}}\right)-\operatorname {artanh} \left({\ frac {u_{0}}{c}}\right)\right\}\end{aligned}}&{\begin{aligned}u(\tau )&=c\tanh \left\{\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau}{c}}\right\}\\\\X(\tau )&=X_{ 0}+{\frac {c^{2}}{\alpha}}\left\{\cosh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right )+{\frac {\alpha \tau}{c}}\right]-\gamma _{0}\right\}\\\\cT(\tau )&=cT_{0}+{\frac {c ^{2}}{\alpha }}\left\{\sinh \left[\operatorname {artanh} \left({\frac {u_{0}}{c}}\right)+{\frac {\alpha \tau }{c}}\right]-{\frac {u_{0}\gamma _{0}}{c}}\right\}\end{aligned}}\end{array}}}}$

Szybkość

Linię świata dla ruchu hiperbolicznego (która od teraz będzie zapisywana jako funkcja czasu własnego) można uprościć na kilka sposobów. Na przykład wyrażenie

${\ Displaystyle X = {\ Frac {c ^ {2}} {\ alfa}} \ lewo (\ cosh {\ Frac {\ alfa \ tau} {c }}-1\prawo)}$

można poddać przesunięciu przestrzennemu o kwotę ${\ Displaystyle c ^ {2}/\ alpha}$ , w ten sposób

${\ Displaystyle X = {\ Frac {c ^ {2}}} {\ alfa}} \ cosh {\ Frac {\ alfa \ tau} {c}}}$ ,

w którym obserwator znajduje się w pozycji ${\ Displaystyle X = c ^ {2} / \ alfa}$ w czasie ${\ displaystyle T = 0}$ . Ponadto, ustawiając i wprowadzając szybkość $\frac {u}{c}}={\frac {\alpha \tau }{c}}}$$artanh$${\ Displaystyle \ eta$ , równania dla ruchu hiperbolicznego redukują się do

${\ Displaystyle cT = x \ sinh \ eta, \ quad X = x \ cosh \ eta}$

 

 

 

 

()

z hiperbolą ${\ Displaystyle X ^ {2} -c ^ {2} T ^ {2} = x ^ {2}}$ .

Naładowane cząstki w ruchu hiperbolicznym

Born (1909), Sommerfeld (1910), von Laue (1911), Pauli (1921) również sformułowali równania pola elektromagnetycznego cząstek naładowanych w ruchu hiperbolicznym. Zostało to rozszerzone przez Hermanna Bondi i Thomasa Golda (1955) oraz Fultona i Rohrlicha (1960)

${\ Displaystyle {\ rozpocząć {wyrównane} E _ {\ rho '}' = & {\ Frac {\ lewo (8e / \ alfa ^ {2} \ prawej) \ rho 'z'} {\ xi ^ {\ pierwsza 3 }}}\\E_{z'}'=&{\frac {-\left(4e/\alpha ^{2}\right)1/\alpha ^{2}+t^{\prime 2}+\ rho ^{\prime 2}-z^{\prime 2}}{\xi ^{\prime 3}}}\\E_{\varphi '}'=&H_{\varphi '}'=H_{z'} '=0\\H_{\varphi '}'=&{\frac {\left(8e/\alpha ^{2}\right)\rho 't'}{\xi ^{\prime 3}}}\ \\xi '=&{\sqrt {\left(1/\alpha ^{2}+t^{\prime 2}-\rho ^{\prime 2}-z^{\prime 2}\right)^ {2}+\left(2\rho '/\alpha \right)^{2}}}\end{wyrównane}}}$

Wiąże się to z kontrowersyjnie dyskutowanym pytaniem, czy ładunki w wieczystym ruchu hiperbolicznym promieniują, czy nie, i czy jest to zgodne z zasadą równoważności – mimo że chodzi o sytuację idealną, bo nieustający ruch hiperboliczny nie jest możliwy. Podczas gdy pierwsi autorzy, tacy jak Born (1909) czy Pauli (1921), argumentowali, że promieniowanie nie powstaje, późniejsi autorzy, tacy jak Bondi i Gold oraz Fulton i Rohrlich, wykazali, że promieniowanie rzeczywiście powstaje.

Właściwy układ odniesienia

Ścieżka światła przechodząca przez E wyznacza pozorny horyzont zdarzeń obserwatora P w ruchu hiperbolicznym.

Główne artykuły: współrzędne Rindlera i właściwy układ odniesienia (płaska czasoprzestrzeń)

W równaniu ( 2 ) dla $ruchu$$hiperbolicznego$ wyrażenie było stałe, podczas gdy prędkość zmienna Jednak, jak zauważył Sommerfeld, można zdefiniować $jednocześnie$ zmienną, $stałą$ . Oznacza to, że równania stają się transformacjami wskazującymi równoczesny spoczynkowy kształt rozpędzonego ciała o współrzędnych hiperbolicznych ${\ Displaystyle (x, y, z, \ eta)}$ widziany przez zbliżającego się obserwatora

${\ Displaystyle cT = x \ sinh \ eta \ quad X = x \ cosh \ eta \ quad Y = y \ czworokąt Z=z}$

Za pomocą tego przekształcenia czas właściwy staje się czasem układu przyspieszonego hiperbolicznie. Współrzędne te, które są powszechnie nazywane współrzędnymi Rindlera (podobne warianty nazywane są współrzędnymi Kottlera-Møllera lub współrzędnymi Lassa ), mogą być postrzegane jako szczególny przypadek współrzędnych Fermiego lub współrzędnych właściwych i są często używane w połączeniu z efektem Unruha . Korzystając z tych współrzędnych, okazuje się, że obserwatorzy w ruchu hiperbolicznym mają pozorny horyzont zdarzeń , poza którym żaden sygnał nie może do nich dotrzeć.

Specjalna transformacja konforemna

Mniej znaną metodą definiowania układu odniesienia w ruchu hiperbolicznym jest zastosowanie specjalnej transformacji konforemnej , składającej się z inwersji , translacji i kolejnej inwersji. Jest powszechnie interpretowana jako transformacja cechowania w przestrzeni Minkowskiego, chociaż niektórzy autorzy alternatywnie używają jej jako transformacji przyspieszenia (patrz Kastrup, aby zapoznać się z krytycznym przeglądem historycznym). Ma formę

${\ Displaystyle X ^ {\ mu} = {\ Frac {x ^ {\ mu} -a ^ {\ mu} x ^ { 2}}{1-2ax+a^{2}x^{2}}}}$

Używając tylko jednego wymiaru przestrzennego przez i dalej upraszczając przez ustawienie i używając przyspieszenia ${\ Displaystyle$$} = (t, x)}$${\ Displaystyle a ^ {\ mu} = (0, - \ alfa / 2)}$ wynika z tego

${\ Displaystyle T = {\ Frac {t} {1- {\ Frac {1} 4}}\alpha {}^{2}t^{2}}},\quad X={\frac {-\alpha t^{2}}{2\left(1-{\frac {1}{ 4}}\alpha {}^{2}t^{2}\right)}}}$

z hiperbolą ${\ Displaystyle \ lewo (X-1 / \ alfa \ prawo) ^ {2} - T ^ {2} = 1 / \ alfa ^ {2}}$ . Okazuje się, że w ${\ Displaystyle t = \ pm (x + 2 / \ alfa)}$ czas staje się pojedynczy, na co Fulton & Rohrlich & Witten zauważają, że należy trzymać się z dala od tej granicy, podczas gdy Kastrup (który jest bardzo krytyczny wobec interpretacji przyspieszenia) zauważa, że ​​jest to jeden z dziwnych wyników tej interpretacji.

Notatki

• Strona Leigh (luty 1936). „Nowa teoria względności. Papier I. Podstawowe zasady i transformacje między przyspieszonymi systemami”. Przegląd fizyczny . 49 (3): 254–268. Bibcode : 1936PhRv...49..254P . doi : 10.1103/PhysRev.49.254 .
• Leigh Page i Norman I. Adams (marzec 1936). „Nowa teoria względności. Artykuł II. Transformacja pola elektromagnetycznego między układami przyspieszonymi a równaniem siły”. Przegląd fizyczny . 49 (6): 466–469. Bibcode : 1936PhRv...49..466P . doi : 10.1103/PhysRev.49.466 .
•   Misner, Charles W .; Thorne, Kip. S. ; Wheeler, John A. (1973), Grawitacja , WH Freeman, rozdział 6, ISBN 0-7167-0344-0
• Rindlera Wolfganga (1960). „Ruch hiperboliczny w zakrzywionej czasoprzestrzeni”. Przegląd fizyczny . 119 (6): 2082–2089. Bibcode : 1960PhRv..119.2082R . doi : 10.1103/PhysRev.119.2082 .
• Ludwik Silberstein (1914): Teoria względności , strona 190.
•     Naber, Gregory L., The Geometry of Minkowski Spacetime , Springer-Verlag, Nowy Jork, 1992. ISBN 0-387-97848-8 (twarda okładka), ISBN 0-486-43235-1 (wydanie w miękkiej oprawie z Dover). s. 58–60.

Linki zewnętrzne

• Często zadawane pytania dotyczące fizyki: Rakieta relatywistyczna
• Mathpages: Przyspieszone podróże , czy równomiernie przyspieszający ładunek promieniuje?