kalendarz Majów

Kalendarz Majów to system kalendarzy używanych w prekolumbijskiej Mezoameryce oraz w wielu współczesnych społecznościach na wyżynach Gwatemali , Veracruz , Oaxaca i Chiapas w Meksyku.

Podstawy kalendarza Majów opierają się na systemie, który był powszechnie używany w całym regionie, datowany co najmniej na V wiek pne. Ma wiele wspólnych aspektów z kalendarzami używanymi przez inne wcześniejsze cywilizacje mezoamerykańskie, takie jak Zapotekowie i Olmekowie , oraz współczesne lub późniejsze, takie jak kalendarze Mixteków i Azteków .

Zgodnie z mitologiczną tradycją Majów, udokumentowaną w relacjach z kolonialnego Yucatec i zrekonstruowaną na podstawie inskrypcji z późnego klasycyzmu i postklasyku, bóstwu Itzamna często przypisuje się przekazanie wiedzy o systemie kalendarzowym Majom przodków, wraz z ogólnym pismem i innymi fundamentalnymi aspektami kultura Majów.

Przegląd

Dalsze informacje: Astronomia Majów

Kalendarz Majów składa się z kilku cykli lub zliczeń o różnej długości. Liczba 260 dni znana jest uczonym jako Tzolkin lub Tzolkʼin . Tzolkin został połączony z 365-dniowym niejasnym rokiem słonecznym znanym jako Haabʼ , tworząc zsynchronizowany cykl trwający 52 Haabʼ, zwany Rundą Kalendarza . Runda kalendarza jest nadal używana przez wiele grup na wyżynach Gwatemali.

Inny kalendarz był używany do śledzenia dłuższych okresów czasu i do wpisywania dat kalendarzowych (tj. identyfikowania, kiedy jedno wydarzenie miało miejsce w stosunku do innych). To jest Długi Rachunek . Jest to liczba dni od mitologicznego punktu wyjścia. Zgodnie z korelacją między kalendarzem Long Count a kalendarzami zachodnimi, akceptowaną przez większość badaczy Majów (znaną jako korelacja Goodmana-Martineza-Thompsona lub GMT), ten punkt początkowy odpowiada 11 sierpnia 3114 r. p.n.e. kalendarza gregoriańskiego lub 6 września według kalendarza juliańskiego (-3113 astronomiczny). Korelację GMT wybrał John Eric Sydney Thompson w 1935 r. na podstawie wcześniejszych korelacji Josepha Goodmana w 1905 r. (11 sierpnia), Juana Martíneza Hernándeza w 1926 r. (12 sierpnia) i samego Thompsona w 1927 r. (13 sierpnia). Ze względu na swój liniowy charakter, Długie Oblicze można było rozszerzyć tak, aby odnosiło się do dowolnej daty z odległej przeszłości lub przyszłości. Ten kalendarz wymagał użycia notacji pozycyjnej , w którym każda pozycja oznaczała rosnącą wielokrotność liczby dni. System liczbowy Majów był zasadniczo dwudziestkowy (tj. podstawa -20), a każda jednostka danej pozycji reprezentowała 20-krotność jednostki pozycji, która ją poprzedzała. Ważny wyjątek dotyczył wartości drugiego rzędu, która zamiast tego reprezentowała 18 × 20, czyli 360 dni, bardziej zbliżona do roku słonecznego niż 20 × 20 = 400 dni. Cykle Długiej Rachuby są niezależne od roku słonecznego.

Wiele inskrypcji Maya Long Count zawiera dodatkowe serie , które dostarczają informacji na temat fazy księżyca , numeru aktualnej lunacji w serii sześciu oraz tego, który z dziewięciu Władców Nocy rządzi.

Śledzono również mniej rozpowszechnione lub słabo poznane cykle, kombinacje i progresje kalendarzowe. Kilka inskrypcji potwierdza liczbę 819 dni . Znane są również powtarzające się zestawy 9 dni (patrz poniżej „Dziewięciu panów nocy”) związane z różnymi grupami bóstw , zwierząt i innych znaczących pojęć.

Tzolkin

Główny artykuł: Tzolkʼin

Tzolkʼin (we współczesnej ortografii Majów ; również powszechnie pisane tzolkin ) to nazwa powszechnie używana przez badaczy Majów dla świętej rundy Majów lub 260-dniowego kalendarza . Słowo tzolkʼin jest neologizmem ukutym w Yucatec Maya i oznacza „liczenie dni” (Coe 1992). Uczeni wciąż dyskutują nad różnymi nazwami tego kalendarza używanymi przez prekolumbijskich Majów. azteckiego nazywał się Tōnalpōhualli w języku nahuatl .

Kalendarz tzolkʼin łączy dwadzieścia nazw dni z numerami trzynastu dni, tworząc 260 unikalnych dni. Służy do określania czasu wydarzeń religijnych i ceremonialnych oraz do wróżenia. Każdy kolejny dzień jest numerowany od 1 do 13, a następnie zaczyna się ponownie od 1. Niezależnie od tego każdemu dniu nadawana jest nazwa w kolejności z listy 20 nazw dni:

Kalendarz Tzolkʼin: nazwane dni i powiązane glify

Sekw. numer 1	Nazwa dnia 2	Przykład glifów 3	XVI w. Jukatek 4	quiche	Zrekonstruowana klasyczna Maja 5		Sekw. numer 1	Nazwa dnia 2	Przykład glifów 3	XVI w. Jukatek 4	quiche	Zrekonstruowana klasyczna Maja 5
01	Mieszam		Mieszam	Imox	Imix (?) / Haʼ (?)		11	Chuwen		Chuen	Bʼatzʼ	(nieznany)
02	Ik'		Ik	Iloraz inteligencji	Ik'		12	Eb'		Eb	MI	(nieznany)
03	Akʼbʼal		Akbal	Aqʼabʼal	Akʼbʼal (?)		13	B'en		Ben	Aj	C'klab
04	Kan		Kan	K'at	Kan (?)		14	Ix		Ix	Iʼx, Balam	Hix (?)
05	Chikchan		Chicchan	Kan	(nieznany)		15	Mężczyźni		Mężczyźni	Tzikin	(nieznany)
06	Kimi		Cimi	Kame	Czam (?)		16	Kʼibʼ		Cib	Ajmaq	(nieznany)
07	Manik'		Manik	Kej	manicz (?)		17	kaban		Kabina	Niej	Chabʼ (?)
08	Lamat		Lamat	Q'anil	Ek' (?)		18	Etz'nab'		Etznab	Tijax	(nieznany)
09	Muluk		Muluc	Toj	(nieznany)		19	Kawak		Cauac	Kawoq	(nieznany)
10	OK		ok	Tzʼiʼ	(nieznany)		20	Ajaw		Ahau	Adżpu	Ajaw
UWAGI: Kolejny numer nazwanego dnia w kalendarzu Tzolkʼin Nazwa dnia w znormalizowanej i poprawionej ortografii gwatemalskiej Academia de Lenguas Mayas Przykładowy glif ( logogram ) dla nazwanego dnia. Należy zauważyć, że dla większości z tych zapisanych jest kilka różnych form; tu pokazane są typowe dla rzeźbionych inskrypcji monumentalnych (są to wersje " kartuszowe ") Imię dnia, jak zapisano z XVI-wiecznych relacji Majów Yucatec , głównie Diego de Landa ; ta ortografia była (do niedawna) szeroko stosowana W większości przypadków nie jest znana rzeczywista nazwa dnia wymawiana w okresie klasycznym (ok. 200–900), kiedy wykonano większość inskrypcji. Podane tutaj wersje (w Majach klasycznych , głównym języku inskrypcji) są rekonstruowane na podstawie dowodów fonologicznych, jeśli są dostępne; A '?' symbol wskazuje, że rekonstrukcja jest wstępna.

Niektóre systemy rozpoczynały liczenie od 1 Imix, po którym następowały 2 Ikʼ, 3 Akʼbʼal itd. Aż do 13 Bʼen. Numery dni następnie zaczynają się ponownie od 1, podczas gdy sekwencja nazwanych dni jest kontynuowana, więc kolejne dni w sekwencji to 1 Ix, 2 Men, 3 Kʼibʼ, 4 Kabʼan, 5 Etzʼnabʼ, 6 Kawak i 7 Ajaw. Po wykorzystaniu wszystkich dwudziestu nazwanych dni zaczęły one teraz powtarzać cykl, podczas gdy sekwencja liczb jest kontynuowana, więc następny dzień po 7 Ajaw to 8 Imix. Powtórzenie tych zazębiających się 13- i 20-dniowych cykli zajmuje zatem 260 dni (to znaczy, aby każda możliwa kombinacja liczby/nazwanego dnia wystąpiła raz).

Najwcześniejszą znaną inskrypcją z Tzolkʼin jest pula uszna Olmeków z 2 Ahau 3 Ceh - 6.3.10.9.0, 2 września -678 (Julian astronomiczny).

Haab'

Miesiące Haabʼ : nazwy i glify w kolejności

Sekw. numer	Nazwa Yucatec	Hieroglif	Okres klasyczny znak glifów	Znaczenie glifu	Zrekonstruowana klasyczna Maja
1	Muzyka pop			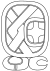	k'anjalaw
2	Woʼ				ik'at
3	Łyk				czakat
4	Sotz'			nietoperz	sotz'
5	Sek				kaseew
6	Xul				chikin
7	Yaxkʼin			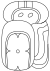	yaxk'in
8	Mol			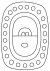	mol
9	Ch'en			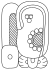czarny	ik'siho'm
10	Yax			zielony	yaxsiho'm
11	Sak			biały	saksiho'm
12	Keh			czerwony	chaksihom
13	Mak				mak
14	Kʼankʼin				uniw
15	Muwan				muwan
16	Patena				paxiil
17	K'ayab			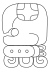	k'anasiiy
18	Kumku			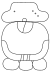	oł
19	Wayeb'			pięć pechowych dni	drogahaab

Główny artykuł: Haab'

Haabʼ składał się z osiemnastu miesięcy po dwadzieścia dni każdy plus okres pięciu dni („bezimiennych dni”) pod koniec roku znanego jako Wayeb' (lub Uayeb w XVI-wiecznej ortografii). Uważano, że pięć dni Wayebʼ to czas niebezpieczny. Foster (2002) pisze: „Podczas Wayeba portale między królestwem śmiertelników a Zaświatami zniknęły. Żadne granice nie powstrzymały bóstw o ​​złych intencjach przed powodowaniem katastrof”. Aby odpędzić te złe duchy, Majowie mieli zwyczaje i rytuały, które praktykowali podczas Wayebʼ. Na przykład ludzie unikali wychodzenia z domów i mycia lub czesania włosów. Bricker (1982) szacuje, że Haabʼ został po raz pierwszy użyty około 550 rpne z początkiem przesilenia zimowego .

Yukatek Maya z epoki kolonialnej , zgodnie z transkrypcją XVI-wiecznych źródeł (w szczególności Diego de Landa i książek, takich jak Chilam Balam of Chumayel ). Analizy fonemiczne nazw glifów Haabʼ w prekolumbijskich inskrypcjach Majów wykazały, że nazwy dla tych dwudziestodniowych okresów różniły się znacznie w zależności od regionu i okresu, odzwierciedlając różnice w języku (językach) i użyciu w języku klasycznym i Epoki postklasyczne poprzedzające ich nagranie przez źródła hiszpańskie.

Każdy dzień w kalendarzu Haabʼ był oznaczony numerem dnia w miesiącu, po którym następowała nazwa miesiąca. Numery dni zaczynały się od glifu tłumaczonego jako „siedziba” nazwanego miesiąca, który jest zwykle uważany za dzień 0 tego miesiąca, chociaż mniejszość traktuje go jako 20 dzień miesiąca poprzedzającego nazwany miesiąc. W tym drugim przypadku posiedzenie Popa to piąty dzień Wayebʼ. Dla większości pierwszy dzień roku był 0 Pop (siedzenie Popu). Potem nastąpił 1 Pop, 2 Pop aż do 19 Pop, potem 0 Wo, 1 Wo i tak dalej.

Ponieważ Haabʼ miał 365 dni, a rok zwrotnikowy trwa 365,2422 dni, dni Haabʼ nie pokrywały się z rokiem zwrotnikowym.

Runda kalendarza

Data rundy kalendarza to data, która podaje zarówno Tzolkʼin, jak i Haabʼ. Ta data powtórzy się po 52 latach Haabʼ lub 18 980 dniach, w rundzie kalendarza. Na przykład obecne tworzenie rozpoczęło się 4 Ahau 8 Kumkʼu. Kiedy ta data się powtarza, nazywa się to zakończeniem rundy kalendarza.

Arytmetycznie czas trwania Rundy Kalendarza jest najmniejszą wspólną wielokrotnością 260 i 365; 18980 to 73 × 260 dni Tzolkʼin i 52 × 365 dni Haabʼ.

Nie każda możliwa kombinacja Tzolkʼin i Haabʼ może wystąpić. W przypadku dni Tzolkʼin Imix, Kimi, Chuwen i Kibʼ dzień Haabʼ może wynosić tylko 4, 9, 14 lub 19; dla Ikʼ, Manikʼ, Ebʼ i Kabʼan dzień Haabʼ może wynosić tylko 0, 5, 10 lub 15; dla Akbʼalʼ, Lamat, Bʼen i Etzʼnabʼ dzień Haabʼ może wynosić tylko 1, 6, 11 lub 16; dla Kʼan, Muluk, Ix i Kawak dzień Haabʼ może wynosić tylko 2, 7, 12 lub 17; a dla Chikchan, Ok, Men i Ajaw dzień Haabʼ może wynosić tylko 3, 8, 13 lub 18.

Nosiciel roku

   „Nosiciel roku” to imię dnia Tzolkʼin , które pojawia się w dniu 0 Pop, pierwszego dnia Haabʼ . Ponieważ istnieje 20 nazw dni Tzolkʼin, 365 dni w Haabʼ, a reszta z 365 podzielona przez 20 to 5 ( 365 = 18 × 20 + 5 ), nazwa dnia Tzolkʼin dla każdego kolejnego 0 Pop będzie wynosić 5 później w cyklu nazw dni Tzolk'in. Podobnie, ponieważ jest 13 liczb dni Tzolk'in, a reszta z 365 podzielona przez 13 to 1 ( 365 = 28 × 13 + 1 ), liczba dni Tzolk'in dla każdego kolejnego 0    Pop będzie o 1 większy niż wcześniej. W związku z tym sekwencja dat Tzolk'in odpowiadająca dacie Haab' 0 Pop jest następująca:

• 1 Ik'
• 2 Manik'
• 3 Eb'
• 4 Kab'an
• 5 Ik'
• ...
• 19 Eb'
• 20 Kab’an
• 1 Ik'
• ...

Tak więc Nosiciele Roku to cztery imiona dni Tzolkʼin, które pojawiają się w tej kolejności: Ik', Manik', Eb' i Kab'an.

„Rok okaziciela” dosłownie tłumaczy koncepcję Majów. Jego znaczenie polega na dwóch faktach. Po pierwsze, cztery lata, na czele których stoją Nosiciele Roku, noszą ich imiona i mają wspólne cechy; dlatego też mają swoje własne przepowiednie i bóstwa opiekuńcze. Ponadto, ponieważ Nosiciele Roku są geograficznie identyfikowani za pomocą znaków granicznych lub gór, pomagają zdefiniować lokalną społeczność.

Opisany powyżej klasyczny system Nosicieli Roku można znaleźć w Tikal iw Kodeksie Drezdeńskim . W okresie późnego klasycznego w Campeche używano innego zestawu Nosicieli Roku. W tym systemie Nosicielami Roku byli Tzolkʼin , którzy zbiegli się z 1 Popem. Byli to Akʼbʼal, Lamat, Bʼen i Edznab. W okresie postklasycznym na Jukatanie był używany trzeci system. W tym systemie nosicielami roku były dni, które zbiegły się z 2 Pop: Kʼan, Muluc, Ix i Kawak. Ten system znajduje się w Kronice Oxkutzcaba. Ponadto tuż przed podbojem Majów przez Hiszpanów Majowie zaczęli numerować dni Haabʼ od 1 do 20. W tym systemie Nosiciele Roku są tacy sami jak w systemie 1 Pop – Campeche. System Classic Year Bearer jest nadal używany na wyżynach Gwatemali oraz w Veracruz, Oaxaca i Chiapas w Meksyku.

Długie liczenie

Wschodnia strona Steli C, Quirigua z mityczną datą powstania 13 baktunów, 0 katunów, 0 tunów, 0 uinali, 0 krewnych, 4 Ahau, 8 Cumku – 11 sierpnia 3114 pne w proleptycznym kalendarzu gregoriańskim

Główny artykuł: mezoamerykański kalendarz Long Count

Ponieważ daty rundy kalendarza powtarzają się co 18 980 dni, czyli około 52 lat słonecznych, cykl powtarza się mniej więcej raz na całe życie, więc do dokładnego zapisania historii potrzebna była bardziej wyrafinowana metoda datowania. Aby określić daty w okresach dłuższych niż 52 lata, mieszkańcy Mezoameryki używali kalendarza Long Count.

Imię Majów na jeden dzień brzmiało kʼin . Dwadzieścia z tych kʼinów jest znanych jako winal lub uinal . Osiemnaście wygranych to jeden tun . Dwadzieścia tunów jest znanych jako kʼatun . Dwadzieścia kʼatunów tworzy bʼakʼtun .

Kalendarz Long Count identyfikuje datę, licząc liczbę dni od daty stworzenia Majów 4 Ahaw, 8 Kumkʼu (11 sierpnia 3114 pne w proleptycznym kalendarzu gregoriańskim lub 6 września w kalendarzu juliańskim - 3113 datowanie astronomiczne). Ale zamiast używać bazy-10 ( dziesiętny ), dni Long Count zostały zliczone w zmodyfikowanym schemacie base-20. Tak więc 0.0.0.1.5 jest równe 25, a 0.0.0.2.0 jest równe 40. Ponieważ zwycięska jednostka resetuje się dopiero po policzeniu do 18, długa rachuba konsekwentnie używa podstawy-20 tylko wtedy, gdy tun jest uważany za podstawową jednostkę pomiar, a nie kʼin; przy czym jednostki kʼin i winal to liczba dni w kadzi. Długa liczba 0.0.1.0.0 reprezentuje 360 ​​dni, a nie 400 w postaci czysto podstawowej 20 ( liczba dziesiętna ).

Istnieją również cztery rzadko używane cykle wyższego rzędu: piktun , kalabtun , kʼinchiltun i alautun .

Ponieważ daty Long Count są jednoznaczne, Long Count szczególnie dobrze nadawał się do wykorzystania na pomnikach. Monumentalne inskrypcje zawierałyby nie tylko 5 cyfr Długiej Rachuby, ale także dwa znaki tzolkʼin, po których następowałyby dwa znaki haabʼ.

Błędna interpretacja mezoamerykańskiego kalendarza Long Count była podstawą powszechnego przekonania, że ​​21 grudnia 2012 roku nastąpi kataklizm . 21 grudnia 2012 był po prostu dniem, w którym kalendarz przeszedł do następnego bʼakʼtun o godzinie 13.0.0.0.0 Long Count. Data rozpoczęcia następnego b'ak'tun (Long Count 14.0.0.0.0) to 26 marca 2407 r. Data rozpoczęcia następnego piktun (pełna seria 20 bʼakʼtunów), o godzinie Long Count 1,0 .0.0.0.0 to 13 października 4772.

Tabela jednostek Long Count

Jednostka Long Count	Okres Długiej Rachunku	Dni	Przybliżone lata słoneczne
1 Kin		1
1 wygrana	20 Kin	20
1 Tun	18 Wina	360	1
1 Kʼatun	20 Cz	7200	20
1 B'ak'tun	20 Kʼatun	144 000	394
1 Piktun	20 B'ak'tun	2 880 000	7885
1 Kalabtun	20 Piktun	57 600 000	157704
1 Kʼinchiltun	20 Kalabtun	1 152 000 000	3154071
1 Alautun	20 Kʼinchiltun	23 040 000 000	63 081 429

Seria uzupełniająca

Wiele inskrypcji z okresu klasycznego zawiera serię glifów znanych jako seria uzupełniająca. Działanie tej serii zostało w dużej mierze opracowane przez Johna E. Teepla . Seria uzupełniająca najczęściej składa się z następujących elementów:

Władcy nocy

Główny artykuł: Władcy nocy

Każdej nocy rządził jeden z dziewięciu władców podziemia. Ten dziewięciodniowy cykl był zwykle zapisywany jako dwa glify: glif odnoszący się do Dziewięciu Władców jako grupy, po którym następował glif oznaczający pana, który miał rządzić następnej nocy.

Seria księżycowa

Seria księżycowa jest zwykle zapisywana jako pięć glifów, które dostarczają informacji o bieżącej lunacji , numerze lunacji w serii sześciu, aktualnie rządzącym bóstwie księżycowym i długości bieżącej lunacji.

Wiek księżyca

Majowie liczyli liczbę dni w obecnej lunacji. Użyli dwóch systemów daty zerowej cyklu księżycowego: albo pierwszej nocy, gdy mogli zobaczyć cienki półksiężyc, albo pierwszego ranka, kiedy nie mogli zobaczyć słabnącego księżyca. Wiek księżyca został przedstawiony za pomocą zestawu glifów, które Majowie wymyślili glify D i E:

• Glif księżyca w nowiu został użyty dla dnia zerowego w cyklu księżycowym.
• Glify D były używane dla ery księżyca dla dni od 1 do 19, z liczbą dni, które minęły od nowiu.
• Dla wieku księżycowego od 20 do 30 używano glifu E z liczbą dni od 20.

Hrabia Lunacji

Majowie liczyli lunacje. Ten cykl pojawia się w serii księżycowej jako dwa glify, które współcześni uczeni nazywają glifami „C” i „X”. Glif C może być poprzedzony liczbą wskazującą lunację. Żaden numer poprzedzający nie oznaczał jednego, podczas gdy liczby od dwóch do sześciu wskazywały na inne lucje. Była też część glifu C, która wskazywała, gdzie to spadło w większym cyklu 18 lunacji. Glifowi C towarzyszył glif „X”, który przedstawiał podobny wzór 18 lunacji.

Długość lunacji

Obecny księżycowy okres synodyczny wynosi około 29,5305877 _średnich dni słonecznych lub około 29 dni 12 godzin 44 minut i 2+ ^7/9 sekundy. W sumie liczba dni na lunację będzie wynosić 29 lub 30 dni, przy czym odstępy 30-dniowe z konieczności będą występować nieco częściej niż odstępy 29-dniowe. Majowie napisali, czy miesiąc księżycowy miał 29, czy 30 dni, jako dwa glify: glif oznaczający długość lunacji, po którym następuje albo glif składający się z glifu księżyca nad wiązką z przyrostkiem 9 dla 29-dniowej lunacji, albo glif księżyca z przyrostkiem 10 dla 30-dniowej lunacji. Ponieważ Majowie nie używali ułamków, lunacje były przybliżone za pomocą wzoru, że 149 lunacji zostało ukończonych w ciągu 4400 dni, co dało dość krótki średni miesiąc wynoszący dokładnie ⁴⁴⁰⁰ / ₁₄₉ = 29+ ^79/149 dni = 29 dni 12 godzin 43 minuty i 29+ _{59/149 sekund} ^, czyli około 29,5302 dni .

Odliczanie 819 dni

Niektóre pomniki Majów zawierają glify, które odnotowują liczbę 819 dni w ich początkowej serii. Można je również znaleźć w kodeksie drezdeńskim . Jest to opisane w Thompsonie. Więcej przykładów tego można znaleźć w Kelley. Każda grupa 819 dni była powiązana z jednym z czterech kolorów i kierunkiem kardynalnym, z którym była powiązana - czarny odpowiadał zachodowi, czerwony wschodowi, biały północy, a żółty południu.

Liczbę 819 dni można opisać na kilka sposobów: Większość z nich odnosi się do glifu „Y” i liczby. Wielu ma również glif oznaczający Kʼawilla – boga z dymiącym lustrem w głowie. Sugerowano, że Kʼawill ma związek z Jowiszem. W kodeksu drezdeńskiego 59 znajdują się Chaacs w czterech kolorach. Towarzyszące teksty rozpoczynają się glifem kierunkowym i czasownikiem dla fraz liczących 819 dni. Anderson przedstawia szczegółowy opis liczby 819 dni.

Krótki rachunek

W późnym okresie klasycznym Majowie zaczęli używać skróconej krótkiej rachuby zamiast długiej rachuby. Przykład tego można znaleźć na ołtarzu 14 w Tikal. W królestwach postklasycznego Jukatanu zamiast długiego liczenia używano krótkiej rachuby. Cykliczne krótkie liczenie to liczba 13 kʼatunów (lub 260 tunów), w których każdy kʼatun został nazwany po jego ostatnim dniu, Ahau („Pan”). 1 Imix został wybrany jako powtarzający się „pierwszy dzień” cyklu, co odpowiada 1 Cipactli w azteckiej liczbie dni. Cykl liczono od katun 11 Ahau do katun 13 Ahau. Ponieważ katun to 20 × 360 = 7200   dni, a reszta z 7200 podzielona przez 13 to 11 ( 7200 = 553×13 + 11 ), numer dnia końcowego każdego kolejnego katun jest o 9 większy niż poprzednio (zawijając się wokół 13, ponieważ tylko 13 dni są używane). Oznacza to, że zaczynając od katun, który zaczyna się od 1 Imix, sekwencja końcowych numerów dni to 11, 9, 7, 5, 3, 1, 12, 10, 8, 6, 4, 2, 13, 11, .. ., wszyscy o imieniu Ahau. Po ostatnim dniu 13 Ahau nastąpił powrót pierwszego dnia 1 Imix. Jest to system, jaki można znaleźć w kolonialnych księgach Chilama Balama . W charakterystyczny dla Mezoameryki sposób, książki te rzutują cykl na krajobraz, z 13 „ Ahauob dzielącymi ziemię Jukatanu na 13 „królestw”.

Zobacz też

• Fenomen 2012 roku
• Religia Majów
• Majanizm
• Tres Zapotes#Stela C
• Astronomia Majów
• kalendarz aztecki

Notatki

•    Aveni, Anthony F. (2001). Skywatchers (pierwotnie opublikowane jako: Skywatchers of Ancient Mexico [1980], poprawione i zaktualizowane red.). Austin: University of Texas Press . ISBN 0-292-70504-2 . OCLC 45195586 .
• Rozruch, Erik (2002). Wstępny klasyczny słownik Majów-angielsko-angielsko-klasyczny z odczytami hieroglificznymi Majów (PDF) . Mesoweb . Źródło 2006-11-10 .
•     Bricker, Victoria R. (luty 1982). „Pochodzenie kalendarza słonecznego Majów”. Bieżąca antropologia . Chicago, IL: University of Chicago Press , sponsorowana przez Wenner-Gren Foundation for Anthropological Research . 23 (1): 101–103. doi : 10.1086/202782 . ISSN 0011-3204 . OCLC 62217742 . S2CID 143962107 .
•   Komory, David Wade (1965). „Czy Majowie znali cykl metoniczny”. Izyda . 56 (3): 348–351. doi : 10.1086/350004 . S2CID 145711182 .
•   Coe, Michael D. (1965). „Model struktury społeczności starożytnych Majów na Nizinie Majów”. Southwestern Journal of Anthropology . 21 . doi : 10.1086/soutjanth.21.2.3629386 . S2CID 130245359 .
•    Coe, Michael D. (1987). Majowie (4. poprawione wydanie). Londyn i Nowy Jork: Thames & Hudson . ISBN 0-500-27455-X . OCLC 15895415 .
•    Coe, Michael D. (1992). Łamanie kodu Majów . Londyn: Tamiza i Hudson . ISBN 0-500-05061-9 . OCLC 26605966 .
•    Foster, Lynn V. (2002). Podręcznik do życia w starożytnym świecie Majów . z przedmową Petera Mathewsa. Nowy Jork: Fakty w aktach . ISBN 0-8160-4148-2 . OCLC 50676955 .
•    Iwanow, Pierre (1971). Mayan Enigma: The Search for Lost Civilization . Elaine P. Halperin (tłum.) (Tłumaczenie Découvertes chez les Mayas , wyd. Angielski). Nowy Jork: Delacorte Press. ISBN 0-440-05528-8 . OCLC 150172 .
•   Jones, Christopher (1984). Odszyfrowywanie hieroglifów Majów . Carl P. Beetz (ilustr.) (przygotowany na weekendowe warsztaty 7 i 8 kwietnia 1984, wyd. 2). Filadelfia: Muzeum Uniwersyteckie, University of Pennsylvania . OCLC 11641566 .
• Kettunen, Harri; Christophe Helmke (2020). Wprowadzenie do hieroglifów Majów: wydanie 17 (PDF) . Couvin, Belgia: Wayeb . Źródło 2020-10-06 .
• Linden, John H. (1996). Warianty Głowy Bóstwa glifu C. Okrągły stół ośmiu Palenque, 1993. s. 343–356.
•   MacDonald, G. Jeffrey (27 marca 2007). „Czy kalendarz Majów przewiduje apokalipsę w 2012 roku?” . Stany Zjednoczone dzisiaj . McLean, Wirginia: Gannett Company . ISSN 0734-7456 . Zarchiwizowane od oryginału w dniu 16.03.2008 . Źródło 2009-05-28 .
•    Milbrath, Susan (1999). Gwiezdni bogowie Majów: astronomia w sztuce, folklorze i kalendarzach . Seria Lindy Schele w badaniach Majów i prekolumbijskich. Austin: University of Texas Press . ISBN 0-292-75225-3 . OCLC 40848420 .
•    Miller, Maria ; Karla Taubego (1993). Bogowie i symbole starożytnego Meksyku i Majów: ilustrowany słownik religii mezoamerykańskiej . Londyn: Tamiza i Hudson. ISBN 0-500-05068-6 . OCLC 27667317 .
• Rice, Prudence M., Pochodzenie kalendarza Majów: pomniki, mitologia i materializacja czasu (Austin, TX: University of Texas Press, 2007).
•    Robinson, Andrew (2000). Historia pisania: alfabety, hieroglify i piktogramy . Londyn i Nowy Jork: Thames & Hudson . ISBN 0-500-28156-4 . OCLC 59432784 .
• Roys, Ralph L. (1967). Księga Chilama Balama z Chumayel . Norman: University of Oklahoma Press .
•    Schele, Linda ; Davida Freidela (1992). A Forest of Kings: The Untold Story of the Ancient Maya (pierwotnie opublikowane New York: Morrow, 1990, przedruk pbk red.). Nowy Jork: Harper Perennial . ISBN 0-688-11204-8 . OCLC 145324300 .
• Schele, Linda; Nickolai Grube; Federico Fahsen (październik 1992). „Seria księżycowa w klasycznych inskrypcjach Majów: nowe obserwacje i interpretacje”. Teksańskie notatki o sztuce, piśmie i kulturze prekolumbijskiej (29).
•    Tedlock, Barbara (1992). Czas i Highland Maya (poprawiona red.). Albuquerque: University of New Mexico Press . ISBN 0-8263-0577-6 . OCLC 7653289 .
• Teeple, John E. (listopad 1931). „Astronomia Majów” (PDF) . Składki na archeologię amerykańską . Tom. I (Pub. 403 wyd.). Waszyngton DC: Carnegie Institution of Washington. s. 29–116.
•    Tedlock, Dennis , wyd. (1985). Popol Vuh: ostateczne wydanie księgi Majów o początkach życia i chwałach bogów i królów . Przetłumaczone przez Tedlocka, Dennisa. z komentarzem opartym na starożytnej wiedzy współczesnych Majów Quiché. Nowy Jork: Simon & Schuster . ISBN 0-671-45241-X . OCLC 11467786 .
•   Tomasz, Cyrus (1897). „Symbole dnia roku Majów” . W JW Powell (red.). Szesnasty raport roczny Biura Etnologii Amerykańskiej dla Sekretarza Smithsonian Institution, 1894–1895 (reprodukcja online EBook). Waszyngton: Biuro Etnologii Amerykańskiej , Smithsonian Institution ; Drukarnia rządu USA . s. 199–266. OCLC 14963920 . Zarchiwizowane od oryginału w dniu 22 stycznia 2007 r. - za pośrednictwem Projektu Gutenberg .
•    Thompson, J. Eric S. (1971). Pismo hieroglificzne Majów: wprowadzenie, wydanie 3 . Cywilizacja serii Indian amerykańskich, nr 56 (wyd. 3). Norman: University of Oklahoma Press . ISBN 0-8061-0447-3 . OCLC 275252 .
• Tozzer, Alfred M. , wyd. (1941). Relación de las cosas de Yucatán Landy: tłumaczenie . Dokumenty z Peabody Museum of American Archaeology and Ethnology, Harvard University vol. 18. Przetłumaczone przez Tozzera, Alfreda M. Charlesa P. Bowditcha i Ralpha L. Roysa (przekład dodatkowy) (przekład Relación de las cosas de Yucatán Diego de Landy [oryginał ok. 1566], z przypisami, komentarzami i załączniki zawierające przetłumaczone fragmenty prac Gaspara Antonio Chi , Tomása Lópeza Medela, Francisco Cervantesa de Salazara i   Antonio de Herrera y Tordesillas . wyd. angielski). Cambridge, MA: Peabody Muzeum Archeologii i Etnologii . OCLC 625693 .
•    Voss, Aleksander (2006). „Astronomia i matematyka”. W Nikolai Grube (red.). Maya: Boscy królowie lasu deszczowego . Eva Eggebrecht i Matthias Seidel (asystent red.). Kolonia, Niemcy: Könemann. s. 130–143. ISBN 978-3-8331-1957-6 . OCLC 71165439 .

Linki zewnętrzne

• Symbole dnia roku Majów w Projekcie Gutenberg 1897, tekst Cyrusa Thomasa
• konwerter daty w FAMSI Ten konwerter używa kalendarza juliańskiego/gregoriańskiego i uwzględnia cykl 819 dni oraz wiek księżycowy.
• Interaktywne kalendarze Majów