Mezoamerykański kalendarz Long Count

Wschodnia strona steli C, Quirigua z mityczną datą powstania 13 baktunów , 0 katunów, 0 tunów, 0 uinali, 0 kins, 4 Ahau 8 Cumku – 11 sierpnia 3114 p.n.e. w proleptycznym kalendarzu gregoriańskim .

Mezoamerykański kalendarz Long Count to niepowtarzalny kalendarz o podstawie 20 i podstawy 18 używany przez kilka prekolumbijskich kultur Mezoameryki , w szczególności Majów . Z tego powodu jest często nazywany Maya Long Count . Korzystając ze zmodyfikowanej liczby dwudziestkowej, kalendarz Long Count identyfikuje dzień, licząc liczbę dni, które upłynęły od mitycznej daty stworzenia , która odpowiada 11 sierpnia 3114 pne w proleptycznym kalendarzu gregoriańskim . Kalendarz Long Count był szeroko stosowany na pomnikach.

Tło

Dwa najczęściej używane kalendarze w prekolumbijskiej Mezoameryce to 260-dniowy Tzolkʼin i 365-dniowy Haabʼ . Równoważne kalendarze azteckie są znane w języku nahuatl jako Tonalpohualli i Xiuhpohualli .

Połączenie daty Haabʼ i Tzolkʼin identyfikuje dzień w kombinacji, który nie występuje ponownie przez 18 980 dni (52 cykle Haabʼ po 365 dni to 73 cykle Tzolkʼin po 260 dni, około 52 lat), okres znany jako Runda kalendarza . Aby zidentyfikować dni w okresach dłuższych niż ten, Mezoamerykanie używali kalendarza Long Count.

Długie okresy zliczania

Detal przedstawiający kolumny glifów z części II wieku n.e. La Mojarra Stela 1 . Lewa kolumna podaje datę Long Count 8.5.16.9.7, czyli 156 rok n.e. Inne widoczne kolumny to glify ze skryptu Epi-Olmeków .

Kalendarz Long Count identyfikuje datę, licząc liczbę dni od daty początkowej, która jest ogólnie obliczana na 11 sierpnia 3114 pne w proleptycznym kalendarzu gregoriańskim lub 6 września w kalendarzu juliańskim (lub -3113 w numeracji roku astronomicznego). Odbyło się wiele dyskusji na temat dokładnej korelacji między kalendarzami zachodnimi a kalendarzami Long Count. Data 11 sierpnia jest oparta na korelacji GMT.

Zakończenie 13 bʼakʼtunów (11 sierpnia 3114 pne) oznacza Stworzenie świata istot ludzkich według Majów. Tego dnia Pan Wzniesionego-Nieba sprawił, że stowarzyszeni bogowie umieścili trzy kamienie w Leżącym-Niebie, Pierwszym-Trzy-Kamiennym-Miejscu. Ponieważ niebo wciąż leżało na pierwotnym morzu, było czarne. Ustawienie trzech kamieni wyśrodkowało kosmos, co pozwoliło na podniesienie nieba, odsłaniając słońce .

Zamiast używać schematu bazowego 10, dni Long Count były liczone w zmodyfikowanym schemacie bazowym 20. W schemacie o czystej podstawie 20 0.0.0.1.5 jest równe 25, a 0.0.0.2.0 jest równe 40. Długie liczenie nie jest jednak czystą podstawą 20, ponieważ druga cyfra od prawej (i tylko ta cyfra) przechodzi do zera, gdy osiągnie 18. [ Potrzebne źródło ] Zatem 0.0.1.0.0 nie reprezentuje 400 dni, ale raczej tylko 360 dni, a 0.0.0.17.19 reprezentuje 359 dni.

Nazwa bʼakʼtun została wymyślona przez współczesnych uczonych. Numerowany Long Count nie był już używany do czasu przybycia Hiszpanów na Półwysep Jukatan , chociaż nienumerowane kʼatuns i tuny były nadal w użyciu. Zamiast tego Majowie używali skróconej krótkiej rachuby .

Tabela jednostek Long Count
Jednostka Long Count
Okres długiego liczenia
Dni
Przybliżone lata słoneczne
1 Kin   1  
1 wygrana 20 Kin 20  
1 Tun 18 Wina 360 1
1 Kʼatun 20 Cz 7200 20
1 B'ak'tun 20 Kʼatun 144 000 394
1 Piktun 20 B'ak'tun 2 880 000 7885
1 Kalabtun 20 Piktun 57 600 000 157704
1 Kʼinchiltun 20 Kalabtun 1 152 000 000 3154071
1 Alautun 20 Kʼinchiltun 23 040 000 000 63 081 429
1 Hablatun 20 Alautun 460 800 000 000 1 261 628 585

Cyfry mezoamerykańskie

Cyfry Majów

Daty Long Count są zapisywane cyframi mezoamerykańskimi, jak pokazano w tej tabeli. Kropka reprezentuje 1 , podczas gdy kreska równa się 5 . Glif powłoki został użyty do przedstawienia koncepcji zerowej. Kalendarz Long Count wymagał użycia zera jako symbolu zastępczego i przedstawia jedno z najwcześniejszych zastosowań koncepcji zera w historii .

W przypadku pomników Majów składnia Long Count jest bardziej złożona. Sekwencja dat jest podana jednorazowo, na początku inskrypcji i rozpoczyna się tak zwanym ISIG (Glif początkowy serii wprowadzającej), który brzmi tzik-a (h) habʼ [patron miesiąca Haabʼ] („czczony był rok-liczenie z patronem [miesiąca]”). Następnie następuje 5 cyfr Długiej Rachuby, a następnie Runda Kalendarzowa (tzolkʼin i Haabʼ) oraz serie uzupełniające . Seria uzupełniająca jest opcjonalna i zawiera dane księżycowe, np. wiek księżyca w danym dniu oraz obliczoną długość aktualnej lunacji . Następnie tekst kontynuuje wszelkie działania, które miały miejsce w tym dniu.

Rysunek pełnej inskrypcji Maya Long Count pokazano poniżej .

Najwcześniejsze długie obliczenia

Najwcześniejsza współczesna inskrypcja Long Count, jaką dotąd odkryto, znajduje się na Steli 2 w Chiapa de Corzo w stanie Chiapas w Meksyku i wskazuje datę 36 pne, chociaż Stela 2 z Takalik Abaj w Gwatemali może być wcześniejsza. [1] Mocno zniszczona inskrypcja Takalika Abaj Stela 2 z Long Count pokazuje 7 bak'tunów , a następnie k'atunów o wstępnym współczynniku 6, ale może to być również 11 lub 16, co daje zakres możliwych dat przypadających między 236 a 19 pne. [ potrzebne źródło ]

Chociaż Takalik Abaj Stela 2 pozostaje kontrowersyjny, ta tabela zawiera go, a także sześć innych artefaktów z ośmioma najstarszymi inskrypcjami Long Count według profesora z Dartmouth Vincenta H. Malmströma (dwa z artefaktów zawierają dwie daty, a Malmström nie obejmuje Takalika Abaj Stela 2). Interpretacje napisów na niektórych artefaktach są różne.

Strona archeologiczna Nazwa data gregoriańska

Korelacja GMT (584283).

Długie liczenie Lokalizacja
Takalik Abaj Stela 2 236 – 19 pne 7.(6,11,16).??.??.? Retalhuleu , Gwatemala
Chiapa de Corzo Stela 2
6 grudnia 36 p.n.e. lub 9 października 182 n.e
7.16.3.2.13 lub 8.7.3.2.13 		Chiapas, Meksyk
Tres Zapotes Stela C 1 września 32 pne 7.16.6.16.18 Veracruz , Meksyk
El Baul Stela 1 11 - 37 n.e


7.18.9.7.12, 7.18.14.8.12, 7.19.7.8.12 lub 7.19.15.7.12 		Escuintla , Gwatemala
Takalik Abaj Stela 5
31 sierpnia 83 n.e. lub 19 maja 103 n.e
8.2.2.10.15 lub 8.3.2.10.15 		Retalhuleu, Gwatemala
Takalik Abaj Stela 5 3 czerwca 126 n.e 8.4.5.17.11 Retalhuleu, Gwatemala
Mojarra Stela 1 19 maja 143 n.e 8.5.3.3.5 Veracruz, Meksyk
Mojarra Stela 1 11 lipca 156 n.e 8.5.16.9.7 Veracruz, Meksyk
W pobliżu La Mojarry Statuetka Tuxtli 12 marca 162 n.e 8.6.2.4.17 Veracruz, Meksyk

Spośród sześciu miejsc trzy znajdują się na zachodnim krańcu ojczyzny Majów, a trzy kilkaset kilometrów dalej na zachód, co prowadzi niektórych badaczy do przekonania, że ​​kalendarz Długiej Rachuby poprzedza Majów. La Mojarra Stela 1, Tuxtla Statuette, Tres Zapotes Stela C i Chiapa Stela 2 są wpisane w Epi-Olmeków , a nie Majów. Z kolei El Baúl Stela 2 został stworzony w Izapan .

Pierwszym jednoznacznym artefaktem Majów jest Stela 29 z Tikal , z datą Long Count 292 n.e. (8.12.14.8.15), ponad 300 lat po Steli 2 z Chiapa de Corzo.

Niedawno, wraz z odkryciem w Gwatemali tekstu kamiennego bloku San Bartolo (miejsce Majów) ( ok. 300 pne), argumentowano, że tekst ten upamiętnia uroczystość zakończenia nadchodzącego okresu. Przewidywano, że ten okres zakończy się między 7.3.0.0.0 a 7.5.0.0.0 — odpowiednio 295 i 256 pne. Poza tym, że jest to najwcześniejszy odkryty do tej pory tekst hieroglificzny Majów, byłby to prawdopodobnie najwcześniejszy jak dotąd dowód glifowy na notację Long Count w Mezoameryce.

Korelacje między zachodnimi kalendarzami a Long Count


Tył Steli C z Tres Zapotes , stanowiska archeologicznego Olmeków. Jest to druga najstarsza odkryta data Long Count. Cyfry 7.16.6.16.18 przekładają się na 1 września 32 pne (gregoriański). Uważa się, że glify otaczające datę są jednymi z niewielu zachowanych przykładów pisma Epi-Olmeków .

Kalendarze Majów i kalendarze zachodnie są skorelowane za pomocą juliańskiego numeru dnia (JDN) daty rozpoczęcia obecnego stworzenia — 13.0.0.0.0, 4 Ajaw , 8 Kumku. Jest to określane jako „stała korelacji”. Ogólnie przyjętą stałą korelacji jest Modified Thompson 2, „ Goodman – Martinez – Thompson ” lub korelacja GMT wynosząca 584 283 dni. Korzystając z korelacji GMT, obecne stworzenie rozpoczęło się 6 września -3113 ( juliański ) - 11 sierpnia 3114 pne w proleptycznym kalendarzu gregoriańskim . Badanie korelacji kalendarza Majów i kalendarza zachodniego jest określane jako kwestia korelacji. Korelacja GMT jest również nazywana 11.16 .

W Breaking the Maya Code Michael D. Coe pisze : „Pomimo oceanów atramentu, które wylano na ten temat, obecnie nie ma najmniejszej szansy, aby ci trzej uczeni (powiązani z GMT, gdy mówili o korelacji) nie byli Prawidłowy ...". Dowody na korelację GMT są historyczne, astronomiczne i archeologiczne:

Historyczne : Kalendarz Okrągłe daty z odpowiadającą im datą juliańską są zapisane w Relación de las cosas de Yucatán Diego de Landy ( napisanym około 1566 r.), Kronice Oxcutzkaba i księgach Chilama Balama . De Landa odnotowuje datę, która jest Tunem kończącym się w Short Count . Oxkutzcab zawiera 12 zakończeń Tun. Bricker i Bricker stwierdzili, że tylko korelacja GMT jest zgodna z tymi datami. Księga Chilama Balama z Chumayel zawiera jedyne kolonialne odniesienie do klasycznych dat z długiej rachuby. Data kalendarza juliańskiego 11.16.0.0.0 (2 listopada 1539) potwierdza korelację GMT.

Annals of the Cakchiquels zawiera liczne daty tzolkʼin skorelowane z datami europejskimi. Potwierdzają one korelację GMT. Weeks, Sachse i Prager dokonali transkrypcji trzech kalendarzy wróżbiarskich z górskiej Gwatemali. Odkryli, że kalendarz z 1772 roku potwierdza korelację GMT. Upadek stolicy Imperium Azteków, Tenochtitlan , nastąpił 13 sierpnia 1521 roku. Wielu różnych kronikarzy pisało, że był to Tzolkʼin ( Tonalpohualli ) z 1 Węża.

Uczeni po podboju, tacy jak Sahagún i Durán , odnotowali Tonalpohualli daty z datą kalendarzową. Wiele rdzennych społeczności w meksykańskich stanach Veracruz, Oaxaca i Chiapas oraz w Gwatemali, głównie mówiących językami Majów Ixil, Mam, Pokomchí i Quiché, utrzymuje Tzolkʼin, aw wielu przypadkach Haabʼ. Wszystko to jest zgodne z korelacją GMT. Munro Edmonsen zbadał 60 mezoamerykańskich kalendarzy, z których 20 ma znane korelacje z kalendarzami europejskimi, i odkrył między nimi niezwykłą spójność oraz to, że tylko korelacja GMT pasuje do dowodów historycznych, etnograficznych i astronomicznych.

Astronomiczny : Każda poprawna korelacja musi pasować do astronomicznej treści klasycznych inskrypcji. Korelacja GMT doskonale sprawdza się w dopasowywaniu danych księżycowych w serii uzupełniającej . Na przykład: Inskrypcja w Świątyni Słońca w Palenque odnotowuje, że w dniu Długiej Rachuby 9.16.4.10.8 w 30-dniowej lunacji upłynęło 26 dni. Ta długa rachuba jest również datą wpisu do tabeli zaćmień w Kodeksie Drezdeńskim .

Stosując trzecią metodę (system Palenque) nów byłby pierwszym wieczorem, kiedy po zachodzie słońca można było spojrzeć na zachód i zobaczyć cienki sierp księżyca. Biorąc pod uwagę naszą współczesną zdolność dokładnego określenia, gdzie patrzeć, kiedy sierp Księżyca jest dogodnie położony, z doskonałego miejsca, w rzadkich przypadkach za pomocą lornetki lub teleskopu, obserwatorzy mogą zobaczyć i sfotografować sierp Księżyca mniej niż jeden dzień po koniunkcji. Ogólnie rzecz biorąc, większość obserwatorów nie widzi Księżyca w nowiu gołym okiem aż do pierwszego wieczoru, kiedy faza Księżyca wynosi co najmniej 1,5 dnia. Jeśli przyjąć, że nów jest pierwszym dniem, w którym dzień fazy księżycowej wynosi co najmniej 1,5 o szóstej wieczorem w strefie czasowej UTC-6 (strefa czasowa obszaru Majów), korelacja GMT będzie dokładnie odpowiadać wielu inskrypcjom księżycowym. W tym przykładzie dzień fazy księżyca wyniósł 27,7 (26 dni licząc od zera) o godzinie 18:00 po koniunkcji o godzinie 1:25 w nocy 10 października 755 i nów Księżyca, kiedy dzień fazy księżycowej wynosił 1,7 o godzinie 18:00 11 października 755 (kalendarz juliański). Działa to dobrze w przypadku wielu, ale nie wszystkich inskrypcji księżycowych.

Współcześni astronomowie odnoszą się do koniunkcji Słońca i Księżyca (czas, kiedy Słońce i Księżyc mają tę samą długość ekliptyczną) jako nowiu. Astronomia mezoamerykańska była obserwacyjna , a nie teoretyczna. Mieszkańcy Mezoameryki nie wiedzieli o kopernikańskiej naturze Układu Słonecznego — nie mieli teoretycznego zrozumienia orbitalnej natury ciał niebieskich. Niektórzy autorzy analizują inskrypcje księżycowe w oparciu o to współczesne rozumienie ruchów Księżyca, ale nie ma dowodów na to, że zrobili to Mezoamerykanie.

Wydaje się, że pierwsza metoda została zastosowana w przypadku innych napisów, takich jak Quirgua stela E (9.17.0.0.0). Korzystając z trzeciej metody, wiek księżyca powinien wynosić 26 dni, podczas gdy w rzeczywistości rejestruje on nów. Używając korelacji GMT o szóstej rano w strefie czasowej -6, byłoby to 2,25 dnia przed koniunkcją, więc można by zarejestrować pierwszy dzień, w którym nie można było zobaczyć słabnącego księżyca.

Fuls przeanalizował te inskrypcje i znalazł mocne dowody na system Palenque i korelację GMT, jednak ostrzegł: „Analiza serii księżycowych pokazuje, że do obliczenia wieku i pozycji księżyca w cyklu sześciomiesięcznym zastosowano co najmniej dwie różne metody i wzory ...”, co daje sezony zaćmień, kiedy Księżyc znajduje się w pobliżu swojego węzła wstępującego lub zstępującego i prawdopodobne jest wystąpienie zaćmienia . Daty przeliczone przy użyciu korelacji GMT są ściśle zgodne z tabelami zaćmień Kodeksu Drezdeńskiego. Kodeks Drezdeński zawiera Wenus tablica rejestrująca heliakalne wschody Wenus. Korzystając z korelacji GMT, zgadzają się one ściśle ze współczesnymi obliczeniami astronomicznymi.

Archeologiczne : Różne przedmioty, które można powiązać z określonymi datami Long Count, zostały datowane izotopowo . W 1959 roku University of Pennsylvania datował węglem próbki z dziesięciu drewnianych nadproży z Tikal . Zostały one wyrzeźbione z datą odpowiadającą 741 AD, przy użyciu korelacji GMT. Średnia data węgla wynosiła 746 ± 34 lata. Niedawno jeden z nich, Nadproże 3 ze Świątyni I, został ponownie przeanalizowany przy użyciu dokładniejszych metod i stwierdzono, że ściśle zgadza się z korelacją GMT.

Jeśli proponowana korelacja musi zgadzać się tylko z jednym z tych dowodów, istnieje wiele innych możliwości. Astronomowie zaproponowali wiele korelacji, na przykład: Lounsbury , Fuls i in. , Böhm i Böhm oraz Stock.

Dzisiaj, 5 marca 2023 ( UTC ), w Long Count jest 13.0.10.6.6 (przy użyciu korelacji GMT).



Korelacje JDN z datą stworzenia Majów (za Thompson 1971, et al. i Aveni 1980)
Nazwa Korelacja
Bowditch 394483
Willsona 438 906
Buźka 482 699
Makemson 489138
Zmodyfikowany Spinden 489383
Spinden 489384
Czajnik 492.622
Dinsmoor 497 879
−4CR 508363
−2CR 546323
Magazyn 556408
Dobry człowiek 584280
Martinez – Hernandez 584281
GMT 584283
Zmodyfikowany Thompson 1 584284
Thompsona (Lounsbury) 584285
Pogo 588626
+2KR 622243
Böhm & Böhm 622261
Kreichgauera 626 927
+4CR 660203
Fuls i in. 660208
Hochleitnera 674265
Schultza 677723
Escalona – Ramos 679108
Vaillanta 679183
Weitzel 774 078
Długie liczenie
(proleptic przed 1582) Korelacja daty gregoriańskiej GMT (584 283). 		Numer dnia juliańskiego
0.0.0.0.0 Czwartek, 1 kwietnia 8239 pne -1 287 717
1.0.0.0.0 Niedziela, 4 lipca 7845 pne -1 143 717
2.0.0.0.0 Środa, 7 października 7451 pne -999717
3.0.0.0.0 Sobota, 9 stycznia 7056 pne -855717
4.0.0.0.0 Wtorek, 14 kwietnia 6662 pne -711717
5.0.0.0.0 piątek, 17 lipca 6268 p.n.e -567717
6.0.0.0.0 Poniedziałek, 20 października 5874 pne -423 717
7.0.0.0.0 Czwartek, 22 stycznia 5479 pne -279 717
8.0.0.0.0 Słońce, 26 kwietnia 5085 pne -135 717
9.0.0.0.0 Środa, 30 lipca 4691 pne 8283
10.0.0.0.0 Sobota, 1 listopada 4297 pne 152283
11.0.0.0.0 Wtorek, 3 lutego 3902 pne 296283
12.0.0.0.0 piątek, 8 maja 3508 p.n.e 440283
13.0.0.0.0 Poniedziałek, 11 sierpnia 3114 p.n.e 584283
1.0.0.0.0 Czwartek, 13 listopada 2720 pne 728283
2.0.0.0.0 Słońce, 16 lutego 2325 pne 872283
3.0.0.0.0 Środa, 21 maja 1931 pne 1 016 283
4.0.0.0.0 Sobota, 23 sierpnia 1537 pne 1 160 283
5.0.0.0.0 Wtorek, 26 listopada 1143 pne 1 304 283
6.0.0.0.0 piątek, 28 lutego 748 p.n.e 1 448 283
7.0.0.0.0 Poniedziałek, 3 czerwca 354 pne 1 592 283
8.0.0.0.0 Czwartek, 5 września 41 roku n.e 1 736 283
9.0.0.0.0 niedziela, 9 grudnia 435 r 1 880 283
10.0.0.0.0 środa, 13 marca 830 2 024 283
11.0.0.0.0 sobota, 15 czerwca 1224 r 2168283
12.0.0.0.0 Wtorek, 18 września 1618 2312283
13.0.0.0.0 pt., 21 grudnia 2012 r 2456283
14.0.0.0.0 poniedziałek, 26 marca 2407 2600283
15.0.0.0.0 Czw, 28 czerwca 2801 2 744 283
16.0.0.0.0 niedziela, 1 października 3195 r 2 888 283
17.0.0.0.0 środa, 3 stycznia 3590 r 3 032 283
18.0.0.0.0 sobota, 7 kwietnia 3984 r 3176283
19.0.0.0.0 wtorek, 11 lipca 4378 r 3320283
1.0.0.0.0.0 piątek, 13 października 4772 3 464 283

2012 i długa rachuba

Główny artykuł: zjawisko 2012 roku

Według Popol Vuh , książki zawierającej szczegóły relacji o stworzeniu znanych Majom Kʼicheʼ z wyżyn epoki kolonialnej, ludzkość żyje w czwartym świecie. Popol Vuh opisuje pierwsze trzy stworzenia, których bogom nie udało się stworzyć, oraz stworzenie odnoszącego sukcesy czwartego świata, w którym umieszczono ludzi. W Długiej Rachubie Majów poprzednie stworzenie zakończyło się pod koniec 13. bʼakʼtuna.

Poprzednie tworzenie zakończyło się długim wyliczaniem 12.19.19.17.19. Kolejny 12.19.19.17.19 miał miejsce 20 grudnia 2012 r. (Kalendarz gregoriański), po którym nastąpił początek 14. bʼakʼtun, 13.0.0.0.0, 21 grudnia 2012 r. Istnieją tylko dwa odniesienia do 13. bʼakʼtun obecnego stworzenia w fragmentaryczny korpus Majów: Tortuguero 6, część inskrypcji władcy i niedawno odkryte schody hieroglificzne La Corona 2, blok V.

Inskrypcje Majów czasami odnoszą się do przyszłych przewidywanych wydarzeń lub upamiętnień, które miałyby miejsce w datach wykraczających poza rok 2012 (to znaczy po ukończeniu 13. bʼakʼtun obecnej epoki). Większość z nich ma postać „dat odległych”, w których podana jest pewna data z Długiego Obliczenia, wraz z Liczbą Odległości, która ma zostać dodana do daty Długiego Obliczenia, aby dotrzeć do tej przyszłej daty.

, na zachodnim panelu w Świątyni Inskrypcji w Palenque , część tekstu wybiega w przyszłość do 80 . Przystąpienie Pakala miało miejsce w dniu rundy kalendarzowej 5 Lamat 1 Mol, w Long Count 9.9.2.4.8, co odpowiada 27 lipca 615 r. n.e. w proleptycznym kalendarzu gregoriańskim ). Robi to, zaczynając od daty urodzenia Pakala 9.8.9.13.0 8 Ajaw 13 Pop (24 marca 603 n.e. gregoriański ) i dodając do niego numer odległości 10.11.10.5.8.

Obliczenia te dotyczą 80. rundy kalendarza od jego wstąpienia na tron, dnia, który również ma datę CR 5 Lamat 1 Mol , ale który leży ponad 4000 lat w przyszłości od czasów Pakala - dnia 21 października w roku 4772. Napis zauważa [ potrzebne źródło ] , że ten dzień przypadałby osiem dni po zakończeniu pierwszego piktuna (od daty stworzenia lub daty zerowej systemu Długiej Rachuby), gdzie piktun jest kolejnym najwyższym rzędem po bʼakʼtun w Długiej Rachubie. Jeśli data zakończenia tego piktun —13 października 4772 — miały być zapisane w notacji Long Count, można było je przedstawić jako 1.0.0.0.0.0. Data 80. rocznicy CR, osiem dni później, to 1.0.0.0.0.8 5 Lamat 1 Mol.

Pomimo rozgłosu wygenerowanego przez datę 2012, Susan Milbrath, kuratorka Sztuki i Archeologii Ameryki Łacińskiej w Muzeum Historii Naturalnej na Florydzie , stwierdziła, że ​​„Nie mamy żadnych zapisów ani wiedzy, że [Majowie] myśleli, że świat się skończy. ” w 2012 r. USA Today pisze : „ Dla starożytnych Majów dotarcie do końca całego cyklu było wielkim świętem” — mówi Sandra Noble, dyrektor wykonawczy Foundation for the Advancement of Mesoamerican Studies w Crystal River , Floryda . Przedstawić dzień 21 grudnia 2012 r. jako dzień zagłady , jest „całkowitą fabrykacją i szansą dla wielu ludzi na zarobienie pieniędzy ” . Instytut Badawczy (MARI) „Wiemy, że Majowie myśleli, że przed tym był jeden, a to sugeruje, że po tym pomyśle byli zadowoleni z pomysłu następnego”.

Konwersja między kalendarzami Long Count i zachodnimi

Obliczanie daty kalendarza zachodniego na podstawie długiej rachuby

Ważne jest, aby znać różnicę między kalendarzami juliańskim i gregoriańskim podczas obliczania daty kalendarza zachodniego na podstawie daty Long Count.

Używając jako przykładu daty Long Count 9.10.11.17.0 (data Long Count wymieniona na tabliczce Pałacu Palenque), najpierw oblicz liczbę dni, które minęły od daty zerowej (11 sierpnia 3114 pne; korelacja GMT, w proleptyczny kalendarz gregoriański , 6 września -3113 juliański astronomiczny).

9 × 144 000 = 1 296 000
10 × 7200 = 72 000
11 × 360 = 3960
17 × 20 = 340
0 × 1 = 0
Suma dni = 1 372 300

Następnie dodaj korelację GMT do całkowitej liczby dni.

1 372 300 + 584 283 = 1 956 583

Ta liczba to dzień juliański .

Aby przekonwertować dzień juliański na datę proleptycznego kalendarza gregoriańskiego :

Od tej liczby odejmij najbliższą mniejszą liczbę dni juliańskich (w poniższej tabeli), w tym przypadku 1 940 206, co odpowiada rokowi 600 n.e.

rok JDN: rok JDN:
1 1 721 060 1100 2122827
100 1 757 585 1200 2159351
200 1 794 109 1300 2195876
300 1 830 633 1400 2232400
400 1 867 157 1500 2 268 924
500 1 903 682 1600 2305448
600 1 940 206 1700 2341973
700 1 976 730 1800 2378497
800 2 013 254 1900 2415021
900 2 049 779 2000 2451545
1000 2 086 303
1 956 583 – 1 940 206 = 16 377

Następnie podziel tę liczbę przez 365 dni (rok niejasny).

16377/365 = 44,86849

Pozostała część to 44,86849 lat, czyli 44 lata i 317 dni. Pełna data roku to 644 n.e. Teraz oblicz liczbę miesięcy i dni, biorąc pod uwagę dni przestępne w ciągu 44 lat. W kalendarzu gregoriańskim co czwarty rok jest rokiem przestępnym, z wyjątkiem wieków, które nie dzielą się równo przez 400 (np. 100, 200, 300). Jeśli rok jest podzielny przez 400 (np. 400, 800 itd.), nie dodawaj dodatkowego dnia. Obliczony rok to 644 rok n.e. Liczba dni przestępnych, pamiętając, że rok 600 nie jest rokiem przestępnym, wynosi 10. Odejmując to od pozostałych 317 dni, otrzymujemy 307; innymi słowy 307 dzień roku 644 n.e., czyli 3 listopada. Podsumowując: data Długiej Rachunku 9.10.11.17.0 odpowiada 3 listopada 644 roku n.e., w Proleptyczny kalendarz gregoriański .

Aby zamienić dzień juliański na astronomiczną datę juliańską / gregoriańską ( proleptyczny kalendarz juliański przed 46 rokiem pne):

Użyj algorytmu astronomicznego, takiego jak metoda Meeusa , aby przekonwertować dzień juliański na datę juliańską/gregoriańską z astronomicznym datowaniem lat ujemnych:

W tym przykładzie:


           
          

  
    

    
     wejście:  dzień juliański  J  =  J  + 0,5  // 1 956 583,5  Z  = część całkowita  J  // 1 956 583  F  = część ułamkowa  J  // 0,5  jeśli  Z  < 2 299 161  to  //  Julian?  A  =  Z  inaczej  alfa  = podłoga ((  Z  - 1 867 216,25) / 36 524,25)  // 15  A  =  Z  + 1 +  alfa  - podłoga (  alfa 
    
    






 / 4.0)  // 2 436 129  // Operacja podłogi zaokrągla liczbę dziesiętną w dół do najbliższej najmniejszej liczby całkowitej.  // Na przykład podłoga (1,5) = 1 i podłoga (−1,5) = -2  koniec, jeśli  B  =  A  + 1524  // 1 958 107  C  = podłoga ((  B  - 122,1) / 365,25)  // 5 360  D  = podłoga (365,25 ×  C  )  // 1 957 740  E  = podłoga ((  B  -  D  ) / 30,6001)  // 11  dzień  =    

 
    

    

 
    

    

 B  -  D  - podłoga (30,6001 ×  E  ) +  F  // 31,5  jeśli  E  < 14  to  miesiąc  =  E  - 1  // 10  inaczej  miesiąc  =  E  - 13  koniec, jeśli  jeśli  miesiąc  > 2  to  rok  =  C  - 4716  // 644  inaczej  rok  =  C  - 4715  koniec jeśli  powrót  (  rok  ,  miesiąc  ,  dzień  )

W tym przykładzie datą juliańską jest południe 31 października 644. Metoda Meeusa nie jest ważna dla ujemnych liczb roku (astronomicznych), dlatego należy zastosować inną metodę, taką jak metoda Petera Bauma.

Obliczanie pełnej daty Long Count

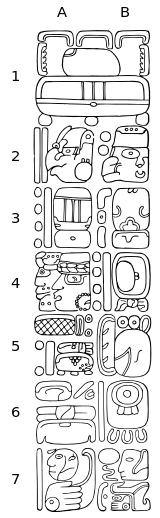
Napis z serii początkowej Chichen Itza . Ta data (glify A2, B2, ..., A5) to 10.2.9.1.9 9 Muluk 7 Sak, co odpowiada 28 lipca 878 (GMT gregoriański).

Pełna data Long Count obejmuje nie tylko pięć cyfr Long Count, ale także dwuznakowe daty Tzolkʼin i dwuznakowe Haabʼ. Pięciocyfrową długą liczbę można zatem potwierdzić za pomocą pozostałych czterech znaków („okrągła data kalendarza”).

Weźmy jako przykład datę rundy kalendarza 9.12.2.0.16 (Długa liczba) 5 Kibʼ (Tzolkʼin) 14 Yaxkʼin (Haabʼ). Poprawność tej daty można sprawdzić za pomocą następującego obliczenia.

Być może łatwiej jest ustalić, ile dni upłynęło od 4 Ajaw 8 Kumkʼu i pokazać, jak wywodzi się data 5 Kibʼ 14 Yaxkʼin.

9 × 144000 = 1296000
12 × 7200 = 86400
2 × 360 = 720
0 × 20 = 0
16 × 1 = 16
Suma dni = 1383136

Obliczanie części daty Tzolkʼin

Data Tzolkʼin jest liczona do przodu od 4 Ajaw. Aby obliczyć numeryczną część daty Tzolkʼin, dodaj 4 do całkowitej liczby dni podanej przez datę, a następnie podziel całkowitą liczbę dni przez 13.

(4 + 1383136) / 13 = 106395 (i 5/13)

Oznacza to, że 106 395 całych 13-dniowych cykli zostało zakończonych, a numeryczna część daty Tzolkʼin wynosi 5.

Aby obliczyć dzień, podziel całkowitą liczbę dni w długim liczeniu przez 20, ponieważ istnieje dwadzieścia nazw dni.

1383136/20 = 69156 (i 16/20)

Oznacza to, że od Ajaw należy liczyć 16 nazw dni. To daje Kibʼ. Dlatego data Tzolkʼin to 5 Kibʼ.

Obliczanie części daty Haabʼ

Data Haabʼ 8 Kumkʼu to dziewiąty dzień osiemnastego miesiąca. Do początku przyszłego roku pozostało 17 dni.

Odejmij 17 dni od sumy, aby znaleźć liczbę pełnych lat Haabʼ.

1383136 - 17 = 1383119 
 na 365
1383119 / 365 = 3789 i (134/365)

Dlatego minęło 3789 pełnych Haabʼ, a pozostałe 134 to 135 dzień w nowym Haabʼ, ponieważ reszta 0 wskazywałaby na pierwszy dzień.

Znajdź miesiąc, w którym jest dany dzień. Dzieląc resztę 134 przez 20, otrzymasz sześć pełnych miesięcy i resztę z 14, co oznacza 15 dzień. Tak więc data w Haabʼ przypada na siódmy miesiąc, czyli Yaxkʼin. Piętnasty dzień Yaxkʼin to 14, więc data Haabʼ to 14 Yaxkʼin.

Tak więc data długiego liczenia 9.12.2.0.16 5 Kibʼ 14 Yaxkʼin jest potwierdzona.

Piktuny i wyższe rzędy

Istnieją również cztery rzadko używane okresy wyższego rzędu powyżej bʼakʼtun: piktun , kalabtun , kʼinchiltun i alautun . Wszystkie te słowa są wynalazkami Majów. Każdy składa się z 20 mniejszych jednostek.

Wiele inskrypcji podaje datę obecnego stworzenia jako dużą liczbę 13 poprzedzających 13.0.0.0.0 4 Ahau 8 Kumkʼu. Na przykład późnoklasycystyczny pomnik z Coba , Stela 1. Data powstania jest wyrażona jako 13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.0.0.0.0, gdzie jednostkami są 13s w dziewiętnaście miejsc większych niż bʼakʼtun. Niektórzy autorzy uważają, że 13 były symbolem ukończenia i nie reprezentują rzeczywistej liczby.

Większość inskrypcji, które ich używają, ma formę dat odległości i Long Reckonings - podają datę bazową, liczbę odległości, która jest dodawana lub odejmowana oraz wynikową Long Count.

Pierwszy przykład poniżej pochodzi od Schele (1987). Drugi pochodzi od Stuarta (2005 s. 60, 77)




Palenque Świątynia Krzyża, tabliczka, Schele (1987 s.) 12.19.13.4.0 8 Ajaw 18 Tzek w poprzedniej epoce 6.14.0 Liczba odległości związana z „datą ery” 13.0.0.0.0 4 Ajaw 8 Kumkʼu




Palenque Temple XIX, South Panel G2-H6 Stuart (2005 s. 60, 77) 12.10.1.13.2 9 Ikʼ 5 Mol (siedzenie GI w poprzedniej epoce) 2.8.3.8.0 1.18.5.3.2 9 Ikʼ 15 Keh (odrodzenie GI, ta data również w Świątyni Krzyża)




Tabliczka inskrypcyjna zawiera następujący napis: 9.8.9.13.0 8 Ajaw 13 Pop 10.11.10.5.8 1.0.0.0.0.8

Kodeks drezdeński zawiera inny sposób zapisywania liczb odległości. To są numery dzwonków. Konkretne daty w kodeksie drezdeńskim są często podawane na podstawie obliczeń obejmujących numery pierścieni. Förstemann je zidentyfikował, ale Wilson (1924) później wyjaśnił sposób, w jaki działają. Numery pierścieni to odstępy dni między datą bazową Ery 4 Ajaw 8 Kumkʼu a wcześniejszą datą bazową pierścienia, gdzie miejsce na liczbę dni w przedziale jest otoczone obrazem zawiązanego czerwonego paska. Do tej wcześniejszej daty Ring Base dodano kolejną liczbę dni do przodu, którą Thompson odnosi się do długiej rundy, prowadzącej do ostatecznej daty w ramach długiej rachuby, która jest podana jako data wejścia do wykorzystania w określonej tabeli w kodeksie.



Numer pierścienia (12) 12.12.17.3.1 13 Imix 9 Wo (7.2.14.19 przed (13) 13.0.0.0.0) numer odległości (0) 10.13.13.3.2 Long Count 10.6.10.6.3 13 Akʼbal 1 Kankʼin


Numer pierścienia (część DN poprzedzająca datę ery) 7.2.14.19 Dodaj numer pierścienia do daty numeru pierścienia, aby osiągnąć 13.0.0.0.0

Thompson zawiera tabelę typowych długich rachunków po Satterwaite.

„Liczby węży” w kodeksie drezdeńskim, s. 61–69, to tabela dat wykorzystująca datę bazową 1.18.1.8.0.16 z poprzedniej epoki (5 482 096 dni).

Zobacz też

Notatki

Bibliografia

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Mesoamerican_Long_Count_calendar&oldid=1140570051 ”