Szerokość

Siatka Ziemi . Pionowe linie od bieguna do bieguna to linie o stałej długości geograficznej lub południki . Okręgi równoległe do równika to linie o stałej szerokości geograficznej lub równoleżniki . Siatka pokazuje szerokość i długość geograficzną punktów na powierzchni. W tym przykładzie południki są rozmieszczone w odstępach co 6°, a równoleżniki w odstępach co 4°.

W geografii szerokość geograficzna to współrzędna określająca położenie północ - południe punktu na powierzchni Ziemi lub innego ciała niebieskiego. Szerokość geograficzną podaje się jako kąt o zakresie od –90° na biegunie południowym do 90° na biegunie północnym, z 0° na równiku . Linie o stałej szerokości geograficznej lub równoleżnikach biegną ze wschodu na zachód jako okręgi równoległe do równika. Szerokość i długość geograficzna są używane razem jako para współrzędnych do określenia lokalizacji na powierzchni Ziemi.

Sam termin „szerokość geograficzna” zwykle odnosi się do szerokości geograficznej określonej poniżej. Krótko mówiąc, geodezyjna szerokość geograficzna punktu to kąt utworzony między wektorem prostopadłym (lub normalnym ) do powierzchni elipsoidy z punktu, a płaszczyzną równika .

Tło

W definicjach szerokości i długości geograficznej stosuje się dwa poziomy abstrakcji. W pierwszym etapie powierzchnia fizyczna jest modelowana przez geoidę , która jest zbliżona do średniego poziomu morza nad oceanami i jego kontynuacji pod masami lądowymi. Drugim krokiem jest przybliżenie geoidy przez prostszą matematycznie powierzchnię odniesienia. Najprostszym wyborem powierzchni odniesienia jest kula , ale geoida jest dokładniej modelowana przez elipsoidę. Definicje szerokości i długości geograficznej na takich powierzchniach odniesienia są szczegółowo opisane w poniższych sekcjach. Linie o stałej szerokości i długości geograficznej razem tworzą siatkę na powierzchni odniesienia. Szerokość geograficzna punktu na rzeczywistej odpowiada szerokości geograficznej odpowiedniego punktu na powierzchni odniesienia, przy czym zgodność przebiega wzdłuż normalnej do powierzchni odniesienia, która przechodzi przez punkt na powierzchni fizycznej. Szerokość i długość geograficzna wraz z pewną specyfikacją wysokości stanowią a geograficzny układ współrzędnych określony w specyfikacji normy ISO 19111.

Ponieważ istnieje wiele różnych elipsoid odniesienia , dokładna szerokość geograficzna obiektu na powierzchni nie jest unikalna: podkreśla to norma ISO, która stwierdza, że „bez pełnej specyfikacji układu współrzędnych odniesienia współrzędne (tj. szerokość i długość geograficzna) są w najlepszym razie niejednoznaczne, aw najgorszym bez znaczenia”. Ma to ogromne znaczenie w dokładnych zastosowaniach, takich jak globalny system pozycjonowania (GPS), ale w powszechnym użyciu, gdzie nie jest wymagana wysoka dokładność, elipsoida odniesienia zwykle nie jest podawana.

W tekstach angielskich kąt szerokości geograficznej, zdefiniowany poniżej, jest zwykle oznaczany małą grecką literą phi ( $ϕ$ lub $φ$ ). Jest mierzony w stopniach , minutach i sekundach lub stopniach dziesiętnych , na północ lub południe od równika. Dla celów nawigacyjnych pozycje podawane są w stopniach i minutach dziesiętnych. Na przykład morska The Needles znajduje się na 50°39.734′ N 001°35.500′ W.

Ten artykuł dotyczy układów współrzędnych dla Ziemi: może być przystosowany do pokrycia Księżyca, planet i innych obiektów niebieskich ( szerokość planetograficzna ).

Aby zapoznać się z krótką historią, zobacz Historia szerokości geograficznej .

Determinacja

W nawigacji na niebie szerokość geograficzną określa się metodą wysokości południkowej . Dokładniejszy pomiar szerokości geograficznej wymaga zrozumienia pola grawitacyjnego Ziemi, aby ustawić teodolity lub określić orbity satelitów GPS. Badanie kształtu Ziemi wraz z jej polem grawitacyjnym jest nauką geodezji .

Szerokość geograficzna na kuli

Perspektywiczny widok Ziemi pokazujący, jak szerokość geograficzna (

i

długość

geograficzna (

) są definiowane na modelu sferycznym Odległość między siatkami wynosi 10 stopni.

Siatka na kuli

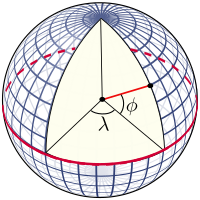
Siatkę tworzą linie o stałej szerokości i stałej długości geograficznej, które są zbudowane w odniesieniu do osi obrotu Ziemi. Podstawowymi punktami odniesienia są bieguny , w których oś obrotu Ziemi przecina powierzchnię odniesienia. Płaszczyzny zawierające oś obrotu przecinają powierzchnię na południkach ; oraz kąt między dowolną płaszczyzną południka a płaszczyzną przechodzącą przez Greenwich ( południk zerowy ) określa długość geograficzną: południki to linie o stałej długości geograficznej. Płaszczyzna przechodząca przez środek Ziemi i prostopadła do osi obrotu przecina powierzchnię po wielkim okręgu zwanym równikiem . Płaszczyzny równoległe do płaszczyzny równikowej przecinają powierzchnię w okręgach o stałej szerokości geograficznej; to są paralele. Równik ma szerokość geograficzną 0°, biegun północny ma 90° szerokości geograficznej północnej (zapisane 90° N lub +90°), a biegun południowy ma szerokość geograficzną 90 ° South (zapisane 90 ° S lub -90 °). Szerokość geograficzna dowolnego punktu to kąt między płaszczyzną równikową a normalną do powierzchni w tym punkcie: normalna do powierzchni kuli przebiega wzdłuż wektora promieniowego.

Szerokość geograficzna, zdefiniowana w ten sposób dla kuli, jest często nazywana szerokością geograficzną sferyczną, aby uniknąć niejednoznaczności z szerokością geograficzną geodezyjną i szerokościami geograficznymi pomocniczymi zdefiniowanymi w kolejnych częściach tego artykułu.

Nazwane szerokości geograficzne na Ziemi

Orientacja Ziemi podczas przesilenia grudniowego.

Oprócz równika ważne są cztery inne równoległości:

koło podbiegunowe	66° 34′ (66,57°) N
zwrotnik Raka	23° 26′ (23,43°) N
zwrotnik Koziorożca	23° 26′ (23,43°) płd
koło podbiegunowe	66° 34′ (66,57°) pł

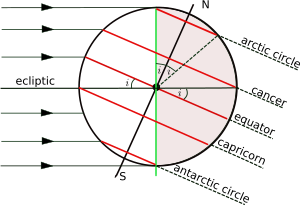
Płaszczyzna orbity Ziemi wokół Słońca nazywana jest ekliptyką , a płaszczyzna prostopadła do osi obrotu Ziemi płaszczyzną równika. Kąt między ekliptyką a płaszczyzną równika nazywany jest różnie nachyleniem osiowym, nachyleniem lub nachyleniem ekliptyki i jest konwencjonalnie oznaczany przez $i$ . Szerokość kręgów tropikalnych jest równa $i$ , a szerokość kręgów polarnych jest jej dopełnieniem (90° - i ). Oś obrotu zmienia się powoli w czasie, a podane tutaj wartości dotyczą bieżącej epoki . Zmienność czasu jest dokładniej omówiona w artykule na temat nachylenia osiowego .

Rysunek przedstawia geometrię przekroju poprzecznego płaszczyzny prostopadłej do ekliptyki i przechodzącej przez środki Ziemi i Słońca w dniu przesilenia grudniowego , kiedy Słońce znajduje się nad głową w pewnym punkcie Zwrotnika Koziorożca . Południowe szerokości geograficzne poniżej koła podbiegunowego są widoczne w ciągu dnia, podczas gdy północne szerokości geograficzne powyżej koła podbiegunowego są widoczne w nocy. Sytuacja odwraca się w czasie przesilenia czerwcowego, kiedy Słońce znajduje się nad Zwrotnikiem Raka. Tylko na szerokościach geograficznych pomiędzy dwoma tropikami czy możliwe jest, aby Słońce znajdowało się bezpośrednio nad głową (w zenicie ).

Na odwzorowaniach map nie ma uniwersalnej zasady, jak powinny wyglądać południki i równoleżniki. Poniższe przykłady pokazują nazwane podobieństwa (jako czerwone linie) na powszechnie używanej projekcji Mercatora i poprzecznej projekcji Mercatora . Na pierwszym równoleżniki są poziome, a południki pionowe, podczas gdy na drugim nie ma dokładnego związku równoleżników i południków z poziomem i pionem: oba są skomplikowanymi krzywymi.

	Normalny Mercator		Merkator poprzeczny
		\

Szerokość geograficzna na elipsoidzie

elipsoidy

W 1687 roku Isaac Newton opublikował Philosophiæ Naturalis Principia Mathematica , w której udowodnił, że obracające się samograwitujące płynne ciało w równowadze przyjmuje postać spłaszczonej elipsoidy. (Ten artykuł używa terminu elipsoida zamiast starszego terminu sferoida ). Wynik Newtona został potwierdzony pomiarami geodezyjnymi w XVIII wieku. (Patrz Łuk południka .) Spłaszczona elipsoida to trójwymiarowa powierzchnia generowana przez obrót elipsy wokół jej krótszej osi (mniejszej osi). „Oblate elipsoida rewolucji” jest skracana do „elipsoidy” w pozostałej części tego artykułu. (Elipsoidy, które nie mają osi symetrii, nazywane są trójosiowymi).

geodezji używano wielu różnych elipsoid odniesienia . W czasach przed satelitami opracowano je tak, aby dobrze pasowały do geoidy na ograniczonym obszarze badania, ale wraz z pojawieniem się GPS naturalne stało się używanie elipsoid referencyjnych (takich jak WGS84 ) ze środkiem w środku masy Ziemi i mniejszą osią wyrównaną z osią obrotu Ziemi. Te geocentryczne elipsoidy znajdują się zwykle w promieniu 100 m (330 stóp) od geoidy. Ponieważ szerokość geograficzna jest definiowana w odniesieniu do elipsoidy, położenie danego punktu jest różne na każdej elipsoidzie: nie można dokładnie określić szerokości i długości geograficznej obiektu geograficznego bez określenia użytej elipsoidy. Wiele map utrzymywanych przez agencje krajowe opiera się na starszych elipsoidach, więc trzeba wiedzieć, w jaki sposób wartości szerokości i długości geograficznej są przekształcane z jednej elipsoidy na drugą. Słuchawki GPS zawierają oprogramowanie do przeprowadzania transformacji układu odniesienia które łączą WGS84 z lokalną elipsoidą odniesienia z powiązaną z nią siatką.

Geometria elipsoidy

Kula o promieniu a ściśnięta wzdłuż osi z , tworząc spłaszczoną elipsoidę obrotową.

O kształcie elipsoidy obrotowej decyduje kształt elipsy, która obraca się wokół swojej mniejszej (krótszej) osi. Wymagane są dwa parametry. Jednym z nich jest niezmiennie promień równikowy, który jest półosią wielką , $a$ . Drugim parametrem jest zwykle (1) promień biegunowy lub półoś mała , $b$ ; lub (2) (pierwsze) spłaszczenie , $f$ ; lub (3) ekscentryczność , $np$ . Te parametry nie są niezależne: są powiązane przez

{\ Displaystyle f = {\ Frac {ab} {a}}, \ qquad e ^ {2} = 2f-f ^ {2}, \ qquad b = a (1-f) = a {\ sqrt {1- e^{2}}}\,.}

Wiele innych parametrów (patrz elipsa , elipsoida ) pojawia się w badaniach geodezji, geofizyki i odwzorowań map, ale wszystkie można wyrazić w kategoriach jednego lub dwóch członków zbioru $a$ , $b$ , $f$ i $e$ . Zarówno $f$ , jak i $e$ są małe i często pojawiają się w obliczeniach w rozwinięciach szeregów; 1/298 . są one rzędu odpowiednio i 0,0818 Wartości dla wielu elipsoid podano na Figurze Ziemi . Elipsoidy odniesienia są zwykle definiowane przez półoś wielką i odwrotne spłaszczenie, $1 / f$ . Na przykład wartościami definiującymi elipsoidę WGS84 używaną przez wszystkie urządzenia GPS są:

$a$ (promień równikowy): dokładnie 6 378 137,0 m
$1 / f$ (odwrotne spłaszczenie): dokładnie 298,257 223 563

z których pochodzą

$b$ (promień biegunowy): 6 356 752 .314 25 m
$e 2$ (mimośrodowość do kwadratu): 0,006 694 379 990 14

Różnica między półosiami głównymi i półosiami mniejszymi wynosi około 21 km (13 mil) i jako ułamek półosi wielkiej odpowiada spłaszczeniu; na monitorze komputera elipsoida mogłaby mieć wymiary 300 na 299 pikseli. Trudno byłoby to odróżnić od kuli o wymiarach 300 na 300 pikseli, więc ilustracje zwykle wyolbrzymiają spłaszczenie.

Szerokości geograficzne geodezyjne i geocentryczne

Definicja geodezyjnej szerokości geograficznej (

)

długości

geograficznej (

) na elipsoidzie Normalna do powierzchni nie przechodzi przez środek, z wyjątkiem równika i biegunów.

Siatka na elipsoidzie jest zbudowana dokładnie tak samo jak na kuli. Normalna w punkcie na powierzchni elipsoidy nie przechodzi przez środek, z wyjątkiem punktów na równiku lub na biegunach, ale definicja szerokości geograficznej pozostaje niezmieniona jako kąt między normalną a płaszczyzną równika. Terminologię określającą szerokość geograficzną należy uściślić, rozróżniając:

Szerokość geodezyjna : kąt między normalną a płaszczyzną równika. Standardowa notacja w publikacjach anglojęzycznych to $ϕ$ . Jest to definicja przyjęta, gdy słowo szerokość geograficzna jest używane bez zastrzeżeń. Do definicji należy dołączyć określenie elipsoidy.
Szerokość geocentryczna (znana również jako szerokość geograficzna sferyczna , po trójwymiarowym kącie biegunowym ): kąt między promieniem (od środka do punktu na powierzchni) a płaszczyzną równika. (Rysunek poniżej ). Nie ma standardowej notacji: przykłady z różnych tekstów obejmują $θ$ , $ψ$ , $q$ , $ϕ'$ , $ϕ c$ , $ϕ g$ . W tym artykule zastosowano $θ$ .

Szerokość geograficzna musi być używana ostrożnie, ponieważ niektórzy autorzy używają jej jako synonimu szerokości geograficznej geodezyjnej, podczas gdy inni używają jej jako alternatywy dla szerokości geograficznej astronomicznej . „Szerokość geograficzna” (bez zastrzeżeń) powinna zwykle odnosić się do szerokości geograficznej geodezyjnej.

Znaczenie określenia odniesienia można zilustrować prostym przykładem. Na elipsoidzie odniesienia dla WGS84 środek Wieży Eiffla ma szerokość geodezyjną 48 ° 51 ′ 29 ″ N lub 48,8583 ° N i długość geograficzną 2 ° 17 ′ 40 ″ E lub 2,2944 ° E. Te same współrzędne na układzie odniesienia ED50 określają punkt na ziemi, który jest oddalony od wieży o 140 metrów (460 stóp). ^{[ Potrzebne źródło ]} Wyszukiwanie w Internecie może dać kilka różnych wartości szerokości geograficznej wieży; elipsoida odniesienia jest rzadko określana.

Odległość południkowa

Długość stopnia szerokości geograficznej zależy od przyjętego kształtu Ziemi .

Odległość południka na kuli

Na kuli normalna przechodzi przez środek, a zatem szerokość geograficzna ( $ϕ$ ) jest równa kątowi wyznaczonemu w środku przez łuk południka od równika do danego punktu. Jeśli odległość południka jest oznaczona przez $m (ϕ) ,$ to

\ circ} }}R\phi _{\mathrm {stopnie} }=R\phi _{\mathrm {radiany} }}

gdzie $R$ oznacza średni promień Ziemi. $R$ jest równe 6371 km lub 3959 milom. Żadna wyższa dokładność nie jest odpowiednia dla $R$ , ponieważ wyniki o wyższej precyzji wymagają modelu elipsoidalnego. Przy tej wartości $R$ długość południka 1 stopnia szerokości geograficznej na kuli wynosi 111,2 km (69,1 mil ustawowych) (60,0 mil morskich). Długość 1 minuty szerokości geograficznej wynosi 1,853 km (1,151 mil ustawowych) (1,00 mil morskich), podczas gdy długość 1 sekundy szerokości geograficznej wynosi 30,8 m lub 101 stóp (patrz mila morska ).

Odległość południka na elipsoidzie

W łuku południka i standardowych tekstach pokazano, że odległość wzdłuż południka od szerokości geograficznej $ϕ$ do równika jest określona wzorem ( $ϕ$ w radianach)

{\ Displaystyle m (\ phi) = \ int _ {0} ^ {\ phi} M (\ phi ') \, d \ phi '= a \ lewo (1-e ^ {2} \ prawo) \ int _ {0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi ' }

gdzie $M (ϕ)$ jest południkowym promieniem krzywizny .

ćwiartki południka od równika do bieguna wynosi

{\ Displaystyle m _ {\ operatorname {p}} = m \ lewo ({\ Frac {\ pi} {2}} \ prawej) \,}

Dla WGS84 odległość ta wynosi 10 001 0,965 729 km .

Ocena całki odległości południka ma kluczowe znaczenie dla wielu badań z zakresu geodezji i odwzorowań map. Można to ocenić, rozszerzając całkę o szereg dwumianowy i całkując wyraz po wyrazie: szczegółowe informacje można znaleźć w łuku południka . Długość łuku południka między dwiema podanymi szerokościami geograficznymi jest dana poprzez zastąpienie granic całki odpowiednimi szerokościami geograficznymi. Długość małego łuku południka jest dana przez

{\ Displaystyle \ delta m (\ fi) = M (\ fi )\,\delta \phi =a\left(1-e^{2}\right)\left(1-e^{2}\sin ^{2}\phi \right)^{-{\frac { 3}{2}}}\,\delta \phi }

${\ Displaystyle \ phi}$	$Δ 1 łac$	$Δ 1 długi$
0°	110,574 km	111,320 km
15°	110,649 km	107,550 km
30°	110,852 km	96,486 km
45°	111,132 km	78,847 km
60°	111,412 km	55.800 km
75°	111,618 km	28,902 km
90°	111,694 km	0,000 km

Kiedy różnica szerokości geograficznej wynosi 1 stopień, co odpowiada $π$ / 180 radianom, odległość łuku wynosi około

{\ Displaystyle \ Delta _ {\ tekst {łac.}} ^ {1} = {\ Frac {\ pi a\left(1-e^{2}\right)}{180^{\circ}\left(1-e^{2}\sin ^{2}\phi \right)^{\frac {3} {2}}}}}

Odległość w metrach (z dokładnością do 0,01 metra) między szerokościami geograficznymi na sferoidzie WGS84 wynosi ${\ Displaystyle \ phi}$ - 0,5 stopnia i ${\ Displaystyle \ phi} + 0,5 stopnia$

{\ Displaystyle \ Delta _ {\ tekst {łac.}} ^ {1} = 111 \ 132,954-559,822 \ sałata 2 \ phi + 1,175 \ cos 4\fi }

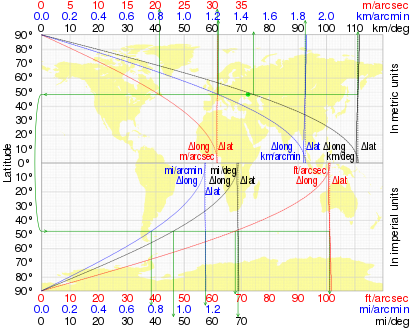
Zmienność tej odległości wraz z szerokością geograficzną (na WGS84 ) pokazano w tabeli wraz z długością stopnia długości geograficznej (odległość wschód-zachód):

{\ Displaystyle \ Delta _ {\ tekst {długi}} ^ {1} = {\ Frac {\ pi a \ cos \ phi}} 180 ^ {\circ }{\sqrt {1-e^{2}\sin ^{2}\phi }}}}\,}

Kalkulator dla dowolnej szerokości geograficznej jest dostarczany przez Narodową Agencję Wywiadu Geoprzestrzennego (NGA) rządu Stanów Zjednoczonych.

Poniższy wykres ilustruje zmianę zarówno stopnia szerokości, jak i stopnia długości geograficznej wraz z szerokością geograficzną.

Definicja szerokości geograficznej geodezyjnej (

ϕ

) i szerokości geocentrycznej (

θ

).

Pomocnicze szerokości geograficzne

Istnieje sześć pomocniczych szerokości geograficznych , które mają zastosowanie do specjalnych problemów w geodezji, geofizyce i teorii odwzorowań map:

Szerokość geocentryczna
Szerokość geograficzna parametryczna (lub zredukowana).
Korekta szerokości geograficznej
Autentyczna szerokość geograficzna
Konformalna szerokość geograficzna
Izometryczna szerokość geograficzna

Wszystkie definicje podane w tej sekcji odnoszą się do lokalizacji na elipsoidzie odniesienia, ale pierwsze dwie pomocnicze szerokości geograficzne, takie jak szerokość geodezyjna, można rozszerzyć, aby zdefiniować trójwymiarowy geograficzny układ współrzędnych, jak omówiono poniżej . Pozostałe szerokości geograficzne nie są wykorzystywane w ten sposób; są używane tylko jako konstrukcje pośrednie w rzutach mapowych elipsoidy odniesienia na płaszczyznę lub w obliczeniach geodezyjnych na elipsoidzie. Ich wartości liczbowe nie są interesujące. Na przykład nikt nie musiałby obliczać autentycznej szerokości geograficznej Wieży Eiffla.

Poniższe wyrażenia podają pomocnicze szerokości geograficzne w kategoriach szerokości geodezyjnej, półosi wielkiej $a$ i ekscentryczności $e$ . (Odwrotności patrz poniżej ). Podane formy, oprócz wariantów notacji, znajdują się w standardowym podręczniku dotyczącym odwzorowań map, a mianowicie „Projekcje map: podręcznik roboczy” autorstwa JP Snydera. Pochodne tych wyrażeń można znaleźć w Adams i publikacjach internetowych Osborne'a i Rappa.

Szerokość geocentryczna

Definicja szerokości geograficznej geodezyjnej (

ϕ

) i szerokości geocentrycznej (

θ

).

Szerokość geocentryczna to kąt między płaszczyzną równikową a promieniem od środka do punktu zainteresowania.

Kiedy punkt znajduje się na powierzchni elipsoidy, zależność między szerokością geocentryczną ( $θ$ ) a szerokością geodezyjną ( $φ$ ) jest następująca:

{\ Displaystyle \ theta (\ phi) = \ tan ^ {-1} \ lewo (\ lewo (1-e ^ {2} \ prawej) \ tan \ phi \ prawej) = \ tan ^ {-1} \ lewo ((1-f)^{2}\tan \phi \right)\,.}

Dla punktów nie leżących na powierzchni elipsoidy zależność obejmuje dodatkowo wysokość elipsoidy h :

{\ Displaystyle \ teta (\ phi, h) = \ dębnik ^ {- 1} \ lewo ( {\frac {N(1-f)^{2}+h}{N+h}}\tan \phi \right)}

Szerokości geodezyjne i geocentryczne są równe na równiku i na biegunach, ale na innych szerokościach geograficznych różnią się o kilka minut kątowych. Przyjmując wartość kwadratu mimośrodu jako 0,0067 (zależy to od wyboru elipsoidy), można wykazać, że maksymalna różnica wynosi około 11,5 minuty łuku na szerokości geodezyjnej ${\ Displaystyle \ phi {-} \ theta}$ około 45° 6′.

Szerokość geograficzna parametryczna (lub szerokość geograficzna zredukowana)

Definicja szerokości parametrycznej (

β

) na elipsoidzie.

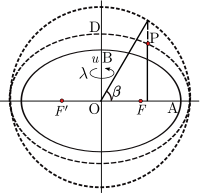
Szerokość parametryczna lub zredukowana szerokość geograficzna $β$ jest określona przez promień poprowadzony od środka elipsoidy do tego punktu $Q$ na otaczającej kuli (o promieniu $a )$ , który jest rzutem równoległym do osi Ziemi punktu $P$ na elipsoidzie na szerokości geograficznej $φ$ . Został wprowadzony przez Legendre'a i Bessela, którzy rozwiązali problemy geodezyjne na elipsoidzie, przekształcając je w równoważny problem dla geodezji sferycznej przy użyciu tej mniejszej szerokości geograficznej. notacja Bessela, $u (ϕ)$ , jest również używany w aktualnej literaturze. Szerokość parametryczna jest powiązana z szerokością geodezyjną przez:

{\ Displaystyle \ beta (\ phi) = \ dębnik ^ {- 1} \left({\sqrt {1-e^{2}}}\tan \phi \right)=\tan ^{-1}\left((1-f)\tan \phi \right)}

Nazwa alternatywna wynika z parametryzacji równania elipsy opisującej przekrój południka. Pod względem współrzędnych kartezjańskich $p$ , odległość od mniejszej osi i $z$ , odległość nad płaszczyzną równika, równanie elipsy wygląda następująco:

{\ Displaystyle {\ Frac {p ^ {2}} {a ^ {2}}} + {\ Frac {z ^ {2}} {b ^ {2}}} = 1 \,.}

Współrzędne kartezjańskie punktu są sparametryzowane przez

{\ Displaystyle p = a \ cos \ beta \,, \ qquad z = b \ sin \ beta \,;}

Cayley zasugerował termin parametryczna szerokość geograficzna ze względu na postać tych równań.

Szerokość parametryczna nie jest wykorzystywana w teorii odwzorowań mapowych. Jego najważniejsze zastosowanie znajduje się w teorii geodezji elipsoidalnej ( Vincenty , Karney).

Korekta szerokości geograficznej

Prostująca szerokość geograficzna $μ to długość południka przeskalowana w$ taki sposób, aby jej wartość na biegunach wynosiła 90 stopni lub $π$ / 2 radiany:

{\ Displaystyle \ mu (\ fi) = {\ Frac {\ pi} {2}} {\ Frac {m (\ fi)} {m _ {\ operatorname { P} }}}}

gdzie odległość południka od równika do szerokości geograficznej $ϕ$ wynosi (patrz łuk południka )

{\ Displaystyle m (\ phi) = a \ lewo (1-e ^ { 2}\right)\int _{0}^{\phi}\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2} }}\,d\phi '\,,}

a długość kwadrantu południka od równika do bieguna ( odległość biegunowa ) wynosi

{\ Displaystyle m _ {\ operatorname {p}} = m \ lewo ({\ Frac {\ pi} {2}} \ prawo) \,.}

Używanie szerokości geograficznej prostującej do zdefiniowania szerokości geograficznej na kuli o promieniu

{\ Displaystyle R = {\ Frac {2m _ {\ operatorname {p}}} {\ pi}}}

definiuje rzut z elipsoidy na kulę w taki sposób, że wszystkie południki mają rzeczywistą długość i jednolitą skalę. Kulę można następnie rzutować na płaszczyznę z rzutem równokątnym , aby uzyskać podwójny rzut z elipsoidy na płaszczyznę, tak że wszystkie południki mają rzeczywistą długość i jednolitą skalę południka. Przykładem zastosowania szerokości geograficznej prostującej jest równoodległy rzut stożkowy . (Snyder, sekcja 16). Duże znaczenie przy konstruowaniu odwzorowania Merkatora poprzecznego ma również szerokość geograficzna rektyfikująca .

Autentyczna szerokość geograficzna

Autaliczna szerokość geograficzna (po grecku oznaczająca „ ten sam obszar ”) $ξ$ daje projekcję równej powierzchni kuli.

{\ Displaystyle \ xi (\ phi) = \ sin ^ {- 1} \ lewo ({\ Frac {q (\ phi)} {q_ { \mathrm {p} }}}\right)}

Gdzie

{\ Displaystyle {\ rozpocząć {wyrównane} q (\ phi) & = {\ Frac {\ lewo (1 -e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}-{\frac {1-e^{2}}{2e}}\ ln \left({\frac {1-e\sin \phi }{1+e\sin \phi}}\right)\\[2pt]&={\frac {\left(1-e^{2} \right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}+{\frac {1-e^{2}}{e}}\tanh ^{-1} (e\sin \phi )\end{wyrównane}}}

I

{\ Displaystyle {\ rozpocząć {wyrównane} q _ {\ operatorname {p}} = q \ lewo ({\ Frac {\ pi} {2}} \ prawej) & = 1- {\ Frac {1-e ^ {2 }}{2e}}\ln \left({\frac {1-e}{1+e}}\right)\\&=1+{\frac {1-e^{2}}{e}} \tanh ^{-1}e\end{wyrównane}}}

a promień kuli przyjmuje się jako

{\ Displaystyle R_ {q} = a {\ sqrt {\ Frac {q _ {\ operatorname {p}}} {2}}} \,.}

Przykładem zastosowania autentycznej szerokości geograficznej jest projekcja stożkowa Albersa o równej powierzchni .

Konformalna szerokość geograficzna

Konforemna szerokość geograficzna $χ$ daje transformację kuli zachowującą kąt ( konforemną ) .

{\ Displaystyle {\ rozpocząć {wyrównane} \ chi (\ phi) & = 2 \ tan ^ {-1} \ lewo [\ lewo ({\ Frac {1 + \ sin \ phi} {1- \ sin \ phi} }\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi}}\right)^{e}\right]^{\frac {1}{2}} -{\frac {\pi }{2}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi}}\right)^{\frac {e}{2}} \right]-{\frac {\pi}{2}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-1}(\tan \phi ) -e\tanh ^{-1}(e\sin \phi )\right)\right]\\&=\nazwa_operatora {gd} \left[\nazwa_operatora {gd} ^{-1}(\phi )-e \tanh ^{-1}(e\sin \phi )\right]\end{wyrównane}}}

gdzie $gd(x)$ jest funkcją Gudermanna . (Zobacz także odwzorowanie Mercatora ).

Konforemna szerokość geograficzna określa przekształcenie elipsoidy w kulę o dowolnym promieniu, tak że kąt przecięcia dowolnych dwóch prostych na elipsoidzie jest taki sam, jak odpowiedni kąt na kuli (tak, że kształt małych elementów jest dobrze zachowany) . Dalsza konformalna transformacja ze sfery na płaszczyznę daje konforemną podwójną projekcję z elipsoidy na płaszczyznę. Nie jest to jedyny sposób generowania takiej projekcji konforemnej. Na przykład „dokładna” wersja projekcji Transverse Mercator na elipsoidzie nie jest podwójnym rzutem. (Obejmuje to jednak uogólnienie konforemnej szerokości geograficznej na płaszczyznę zespoloną).

Izometryczna szerokość geograficzna

Izometryczna szerokość geograficzna $ψ$ jest wykorzystywana przy opracowywaniu elipsoidalnych wersji normalnego odwzorowania Merkatora i poprzecznego odwzorowania Merkatora . Nazwa „izometryczny” wynika z faktu, że w dowolnym punkcie elipsoidy równe przyrosty $ψ$ i długości geograficznej $λ$ powodują równe przemieszczenia odległości odpowiednio wzdłuż południków i równoleżników. Siatka wyznaczona liniami stałej $ψ$ i $stałej$ λ , dzieli powierzchnię elipsoidy na siatkę kwadratów (różnej wielkości). Izometryczna szerokość geograficzna na równiku wynosi zero, ale szybko odbiega od szerokości geodezyjnej, dążąc do nieskończoności na biegunach. Konwencjonalny zapis jest podany w Snyder (strona 15):

{\ Displaystyle {\ rozpocząć {wyrównane} \ psi (\ fi) & = \ ln \ lewo [\ tan \ lewo ({\ Frac {\ pi} {4}} + {\ Frac {\ fi} {2}} \right)\right]+{\frac {e}{2}}\ln \left[{\frac {1-e\sin \phi }{1+e\sin \phi }}\right]\\& =\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e \tanh ^{-1}(e\sin \phi ).\end{wyrównane}}}

Dla normalnego rzutu Merkatora (na elipsoidę) funkcja ta określa rozstaw równoleżników: jeżeli długość równika na rzucie wynosi $E$ (jednostki długości lub piksele), to odległość $y$ równoleżnika o szerokości geograficznej $φ$ od równik jest

{\ Displaystyle y (\ fi) = {\ Frac {E} {2 \ pi}} \ psi (\ fi) \,.}

Izometryczna szerokość geograficzna $ψ$ jest ściśle związana z konforemną szerokością geograficzną $χ$ :

{\ Displaystyle \ psi (\ phi) = \ nazwa operatora {gd} ^ {- 1} \ chi (\ phi) \,.}

Formuły i szeregi odwrotne

Wzory w poprzednich sekcjach podają pomocniczą szerokość geograficzną wyrażoną jako szerokość geodezyjna. Wyrażenia na szerokość geograficzną geocentryczną i parametryczną można odwrócić bezpośrednio, ale jest to niemożliwe w czterech pozostałych przypadkach: szerokości geograficznej rektyfikacyjnej, autentycznej, konforemnej i izometrycznej. Istnieją dwa sposoby postępowania.

Pierwsza to numeryczne odwrócenie równania definiującego dla każdej poszczególnej wartości pomocniczej szerokości geograficznej. Dostępne metody to iteracja punktu stałego i znajdowanie pierwiastka Newtona-Raphsona .
- Podczas konwersji z izometrycznego lub konforemnego na geodezyjny, dwie iteracje Newtona-Raphsona dają podwójną precyzję .
Innym, bardziej użytecznym podejściem jest wyrażenie pomocniczej szerokości geograficznej jako szeregu w kategoriach szerokości geodezyjnej, a następnie odwrócenie szeregu metodą rewersji Lagrange'a . Szeregi takie przedstawia Adams, który wykorzystuje rozwinięcia szeregów Taylora i podaje współczynniki w postaci ekscentryczności. Osborne wyprowadza szeregi do dowolnej kolejności za pomocą pakietu algebry komputerowej Maxima i wyraża współczynniki zarówno pod względem ekscentryczności, jak i spłaszczenia. Metoda szeregowa nie ma zastosowania do szerokości geograficznej izometrycznej i należy znaleźć konforemną szerokość geograficzną w kroku pośrednim.

Numeryczne porównanie szerokości geograficznych pomocniczych

Wykres po prawej pokazuje różnicę między szerokością geodezyjną a pomocniczymi szerokościami geograficznymi innymi niż szerokość izometryczna (która na biegunach rozbiega się do nieskończoności) dla przypadku elipsoidy WGS84. Różnice pokazane na wykresie wyrażone są w minutach kątowych. Na półkuli północnej (dodatnie szerokości geograficzne) θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ ; na półkuli południowej (szerokości geograficzne ujemne) nierówności są odwrócone, z równością na równiku i biegunach. Chociaż wykres wydaje się być symetryczny pod kątem około 45°, minima krzywych w rzeczywistości leżą między 45° 2′ a 45° 6′. Niektóre reprezentatywne punkty danych podano w poniższej tabeli. Szerokości geograficzne konforemne i geocentryczne są prawie nie do odróżnienia, co wykorzystywano w czasach kalkulatorów ręcznych do przyspieszenia konstruowania odwzorowań map.

Dla pierwszego rzędu w spłaszczaniu f , szerokości geograficzne pomocnicze można wyrazić jako ζ = ϕ − Cf sin 2 ϕ gdzie stała C przyjmuje wartości [ 1 ⁄ 2 , 2 ⁄ 3 , 3 ⁄ 4 , 1, 1] dla ζ = [ β , ξ , μ , χ , θ ].

Przybliżona różnica od szerokości geograficznej geodezyjnej ( $ϕ$ )
$ϕ$	Parametryczny $β - ϕ$	Autentyczny $ξ - ϕ$	Prostowanie $μ - ϕ$	Konforemny $χ - ϕ$	Geocentryczny $θ - ϕ$
0°	0,00′	0,00′	0,00′	0,00′	0,00′
15°	−2,88′	−3,84′	−4,32′	−5,76′	−5,76′
30°	−5.00′	−6,66′	−7,49′	−9,98′	−9,98′
45°	−5,77′	−7,70′	−8,66′	−11,54′	−11,55′
60°	−5.00′	−6,67′	−7,51′	−10.01′	−10,02′
75°	−2,89′	−3,86′	−4,34′	−5,78′	−5,79′
90°	0,00′	0,00′	0,00′	0,00′	0,00′

Układy szerokości i współrzędnych

Geodezyjna szerokość geograficzna lub dowolna z pomocniczych szerokości geograficznych określonych na elipsoidzie odniesienia tworzy wraz z długością geograficzną dwuwymiarowy układ współrzędnych na tej elipsoidzie. Aby określić położenie dowolnego punktu, konieczne jest rozciągnięcie takiego układu współrzędnych na trzy wymiary. W ten sposób wykorzystywane są trzy szerokości geograficzne: szerokość geograficzna geodezyjna, geocentryczna i parametryczna są używane odpowiednio we współrzędnych geodezyjnych, sferycznych współrzędnych biegunowych i współrzędnych elipsoidalnych.

Współrzędne geodezyjne

P(ɸ, λ, h)

W dowolnym punkcie $P$ rozważ prostą $PN$ , która jest normalna do elipsoidy odniesienia. Współrzędne geodezyjne $P(ɸ, λ, h)$ to szerokość i długość geograficzna punktu $N$ na elipsoidzie oraz odległość $PN$ . Wysokość ta różni się od wysokości nad geoidą lub wysokości odniesienia, takiej jak wysokość nad poziomem morza w określonej lokalizacji. Kierunek $PN$ będzie również różnił się od kierunku pionowego pionu. Relacja tych różnych wysokości wymaga znajomości kształtu geoidy, a także pola grawitacyjnego Ziemi.

Sferyczne współrzędne biegunowe

Współrzędna geocentryczna związana ze sferycznymi współrzędnymi biegunowymi

P(r, θ', λ)

Geocentryczna szerokość geograficzna $θ$ jest dopełnieniem kąta biegunowego lub współrzędnej geograficznej $θ'$ w konwencjonalnych sferycznych współrzędnych biegunowych , w których współrzędne punktu to $P (r, θ', λ)$ , gdzie $r$ jest odległością $P$ od centrum $O$ , $θ '$ to kąt między wektorem promienia a osią biegunową i $λ$ jest długością geograficzną. Ponieważ normalna w ogólnym punkcie elipsoidy nie przechodzi przez środek, jasne jest, że punkty $P'$ na normalnej, z których wszystkie mają tę samą szerokość geodezyjną, będą miały różne szerokości geocentryczne. Sferyczne biegunowe układy współrzędnych są wykorzystywane w analizie pola grawitacyjnego.

Współrzędne elipsoidalno-harmoniczne

Współrzędne elipsoidalne

P(u, β, λ)

Szerokość parametryczną można również rozszerzyć na trójwymiarowy układ współrzędnych. Dla punktu $P$ nie leżącego na elipsoidzie odniesienia (półosie $OA$ i $OB$ ) skonstruuj elipsoidę pomocniczą, która jest konfokalna (te same ogniska $F$ , $F'$ ) z elipsoidą odniesienia: warunkiem koniecznym jest, aby iloczyn $ae$ półosi wielkiej a ekscentryczność jest taka sama dla obu elipsoid. Niech $u$ będzie półoś małą ( $OD$ ) elipsoidy pomocniczej. Dalej niech $β$ będzie parametryczną szerokością geograficzną $P$ na elipsoidzie pomocniczej. Zbiór $(u, β, λ)$ określa współrzędne elipsoidalno-harmoniczne lub po prostu współrzędne elipsoidalne (chociaż termin ten jest również używany w odniesieniu do współrzędnych geodezyjnych). Współrzędne te są naturalnym wyborem w modelach pola grawitacyjnego obracającego się ciała elipsoidalnego. Powyższe dotyczy elipsoidy dwuosiowej (sferoidy, jak we współrzędnych sferoidalnych spłaszczonych ); dla uogólnienia zobacz trójosiowe współrzędne elipsoidalne .

Konwersje współrzędnych

Nie przedstawiono tu zależności między powyższymi układami współrzędnych, a także współrzędnych kartezjańskich. Transformację między współrzędnymi geodezyjnymi i kartezjańskimi można znaleźć w konwersji współrzędnych geograficznych . Relacja biegunów kartezjańskich i sferycznych jest podana w sferycznym układzie współrzędnych . Relacja współrzędnych kartezjańskich i elipsoidalnych jest omówiona w Torge.

Szerokość astronomiczna

Ocean
Elipsoida
Lokalna linia pionu
Kontynent
Geoida

Szerokość geograficzna astronomiczna ( $Φ$ ) to kąt między płaszczyzną równikową a rzeczywistym kierunkiem pionowym w punkcie na powierzchni. Prawdziwy pion, kierunek pionu , jest również kierunkiem grawitacji (wypadkowa przyspieszenia grawitacyjnego (opartego na masie) i przyspieszenia odśrodkowego ) na tej szerokości geograficznej. Astronomiczna szerokość geograficzna jest obliczana na podstawie kątów mierzonych między zenitem a gwiazdami, których deklinacja jest dokładnie znana.

Ogólnie rzecz biorąc, prawdziwy pion w punkcie na powierzchni nie pokrywa się dokładnie ani z normalną do elipsoidy odniesienia, ani normalną do geoidy. Geoida to wyidealizowany, teoretyczny kształt „na średnim poziomie morza”. Punkty na lądzie nie leżą dokładnie na geoidzie, a na pion w punkcie w określonym czasie wpływają siły pływowe, które teoretyczna geoida uśrednia. Kąt między normalnymi astronomicznymi i geodezyjnymi nazywany jest odchyleniem pionowym i zwykle wynosi kilka sekund łuku, ale jest ważny w geodezji.

Astronomicznej szerokości geograficznej nie należy mylić z deklinacją , współrzędnych , których astronomowie używają w podobny sposób do określania położenia kątowego gwiazd na północ/południe od równika niebieskiego (patrz współrzędne równikowe ), ani z szerokością ekliptyczną , współrzędną używaną przez astronomów do określania położenie kątowe gwiazd na północ/południe od ekliptyki (patrz współrzędne ekliptyki ).

Zobacz też

przypisy

Cytaty

Linki zewnętrzne

GEONets Names Server Archived 2008-03-09 at the Wayback Machine , dostęp do bazy danych National Geospatial-Intelligence Agency (NGA) zawierającej nazwy obcych obiektów geograficznych.
Zasoby do określania szerokości i długości geograficznej Zarchiwizowane 2008-05-19 w Wayback Machine
Konwersja stopni dziesiętnych na stopnie, minuty, sekundy - Informacje o konwersji dziesiętnej na sześćdziesiętną
Zamień stopnie dziesiętne na stopnie, minuty, sekundy
Obliczanie odległości na podstawie szerokości i długości geograficznej - wersja JavaScript
Badanie szerokości geograficznej z XVI wieku
Określenie szerokości geograficznej przez Francisa Drake'a na wybrzeżu Kalifornii w 1579 roku