Sygnał analityczny

W matematyce i przetwarzaniu sygnałów sygnał analityczny jest funkcją o wartościach zespolonych , która nie ma ujemnych składowych częstotliwości. Rzeczywista i urojona część sygnału analitycznego to funkcje o wartościach rzeczywistych powiązane ze sobą za pomocą transformaty Hilberta .

Analityczną reprezentacją funkcji o wartościach rzeczywistych jest sygnał analityczny , zawierający pierwotną funkcję i jej transformatę Hilberta. Ta reprezentacja ułatwia wiele manipulacji matematycznych. Podstawową ideą jest to, że ujemne składowe częstotliwościowe transformaty Fouriera (lub widma ) funkcji o wartościach rzeczywistych są zbędne ze względu na hermitowską symetrię takiego widma. Te ujemne składowe częstotliwości można odrzucić bez utraty informacji, pod warunkiem, że zamiast tego chce się zająć funkcją o wartościach zespolonych. To sprawia, że niektóre atrybuty funkcji są bardziej dostępne i ułatwiają wyprowadzanie technik modulacji i demodulacji, takich jak jednowstęga boczna.

Dopóki manipulowana funkcja nie ma ujemnych składowych częstotliwości (to znaczy, że nadal jest analityczna ), konwersja ze złożonej z powrotem na rzeczywistą jest tylko kwestią odrzucenia części urojonej. Reprezentacja analityczna jest uogólnieniem koncepcji wskazów : podczas gdy wskaz jest ograniczony do niezmiennej w czasie amplitudy, fazy i częstotliwości, sygnał analityczny dopuszcza parametry zmienne w czasie.

Definicja

Funkcja transferu do tworzenia sygnału analitycznego

Jeśli $funkcją$ o wartościach rzeczywistych z transformatą Fouriera $względem$ $= 0}$ transformacja f { oś:

{\ Displaystyle S (-f) = S (f) ^ {*},}

gdzie ${\ Displaystyle S (f) ^ {*}}$ jest złożonym koniugatem ${\ Displaystyle S (f)}$ . Funkcja:

{\ Displaystyle {\ rozpocząć {wyrównane} S _ {\ operatorname {a}} (f) i \ trójkąt q {\ rozpocząć {przypadki} 2S (f) i {\text{for}}\ f>0,\\S(f),&{\text{for}}\ f=0,\\0,&{\text{for}}\ f<0\end {przypadki}}\\&=\underbrace {2\nazwa_operatora {u} (f)} _{1+\nazwa_operatora {sgn}(f)}S(f)=S(f)+\nazwa_operatora {sgn}( f)S(f),\end{wyrównane}}}

Gdzie

${\ Displaystyle \ operatorname {u} (f)}$ jest funkcją skokową Heaviside'a ,
${\ Displaystyle \ operatorname {sgn} (f)}$ jest funkcją znaku ,

zawiera tylko nieujemne składowe częstotliwości ${\ Displaystyle S (f)}$ . A operacja jest odwracalna ze względu na hermitowską symetrię ${\ Displaystyle S (f)}: S ( fa ) {\ Displaystyle S (f)$ }

{\ Displaystyle {\ rozpocząć {wyrównane} S (f) & = {\ rozpocząć {przypadki} {\ Frac {1} {2}} S _ {\ operatorname {a}} (f) i {\ tekst {for} }\ f>0,\\S_{\mathrm {a}}(f),&{\text{for}}\ f=0,\\{\frac {1}{2}}S_{\mathrm { a} }(-f)^{*},&{\text{for}}\ f<0\ {\text{(symetria hermitowska)}}\end{przypadki}}\\&={\frac {1 }{2}}[S_{\mathrm {a}}(f)+S_{\mathrm {a}}(-f)^{*}].\end{wyrównane}}}

Sygnał analityczny jest odwrotną transformatą Fouriera S za $S _$ $(f)$ \ }

{\ Displaystyle {\ rozpocząć {wyrównane} s _ {\ operatorname {a}} (t) i \ trójkątq {\ mathcal {F}}^{-1}[S_{\mathrm {a}}(f)]\\&={\mathcal {F}}^{-1}[S(f)+\nazwa operatora {sgn}( f)\cdot S(f)]\\&=\underbrace {{\mathcal {F}}^{-1}\{S(f)\}} _{s(t)}+\overbrace {\underbrace {{\mathcal {F}}^{-1}\{\operatorname {sgn}(f)\}} _{j{\frac {1}{\pi t}}}*\underbrace {{\mathcal { F}}^{-1}\{S(f)\}} _{s(t)}} ^{\text{splot}}\\&=s(t)+j\underbrace {\left[{ 1 \over \pi t}*s(t)\right]} _{\operatorname {\mathcal {H}} [s(t)]}\\&=s(t)+j{\hat {s} }(t),\end{wyrównane}}}

Gdzie

${\ Displaystyle {\ kapelusz {s}} (t) \ triangleq \ nazwa operatora {\ mathcal {H}} [s (t)]}$ jest transformatą Hilberta ${\ Displaystyle s (t)}$ ;
${\ displaystyle *}$ jest binarnym operatorem splotu ;
${\ displaystyle j}$ to jednostka urojona .

Zauważając $_$ _ składowe częstotliwości :

{\ Displaystyle s _ {\ operatorname {a}} (t) = s (t) * \ underbrace {\ lewo [\ delta (t) + j {1 \ ponad \ pi t} \ prawo]} _ {{\ mathcal {F}}^{-1}\{2u(f)\}}.}

Ujemne składowe częstotliwości

Ponieważ ${\ Displaystyle s (t) = \ operatorname {Re} [s _ {\ operatorname {a}} (t)]} , przywrócenie$ ujemnych składowych częstotliwości jest $,$ kwestia się Możemy również zauważyć $,$ że zawiera składowe I dlatego ${\ Displaystyle s (t) = \ operatorname {Re} [s_ {\ operatorname {a}} ^ {*} (t)]}$ przywraca tłumione składowe o dodatniej częstotliwości. Inny punkt widzenia jest taki, że składowa urojona w obu przypadkach jest wyrazem, który odejmuje składowe częstotliwości od ${\ displaystyle s (t).}$ Operator ${\ displaystyle \ operatorname {Re}}$ usuwa odejmowanie, dając wrażenie dodawania nowych składników.

Przykłady

Przykład 1

{\ Displaystyle s (t) = \ cos (\ omega t)}

gdzie

{\ Displaystyle \ omega > 0.}

Następnie:

{\ Displaystyle {\ rozpocząć {wyrównane} {\ kapelusz {s}} (t) & = \ cos \ lewo (\ omega t - {\ Frac {\ pi} {2}} \ prawej) = \ sin (\ omega t),\\s_{\mathrm {a}}(t)&=s(t)+j{\kapelusz {s}}(t)=\cos(\omega t)+j\sin(\omega t )=e^{j\omega t}.\end{wyrównane}}}

Ostatnią równością jest wzór Eulera , którego następstwem jest $w$ _ ogólnie rzecz biorąc, analityczną reprezentację prostej sinusoidy uzyskuje się, wyrażając ją w postaci zespolonych wykładników, odrzucając składową ujemną i podwajając składową dodatnią. A analityczna reprezentacja sumy sinusoid jest sumą analitycznych reprezentacji poszczególnych sinusoid.

Przykład 2

Tutaj używamy wzoru Eulera, aby zidentyfikować i odrzucić ujemną częstotliwość.

{\ Displaystyle s (t) = \ sałata (\ omega t + \theta )={\frac {1}{2}}\left(e^{j(\omega t+\theta)}+e^{-j(\omega t+\theta)}\right)}

Następnie:

{\ Displaystyle s _ {\ operatorname {a}} (t) = {\ rozpocząć {przypadki} e ^ {j (\ omega t + \ teta)} \ \ = \ e ^{j|\omega |t}\cdot e^{j\theta },&{\text{if}}\ \omega >0,\\e^{-j(\omega t+\theta )}=\ e^{j|\omega |t}\cdot e^{-j\theta },&{\text{if}}\ \omega <0.\end{przypadki}}}

Przykład 3

To kolejny przykład wykorzystania metody transformaty Hilberta do usunięcia ujemnych składowych częstotliwości. Zauważmy, że nic nie stoi na przeszkodzie, aby obliczyć $(t)}$ \ $operatorname {a}}$ . Ale może to nie być reprezentacja odwracalna, ponieważ oryginalne widmo ogólnie nie jest symetryczne. Więc z wyjątkiem tego przykładu, ogólna dyskusja zakłada, że wartości rzeczywiste są ${\ displaystyle s (t)}$ .

{\ Displaystyle s (t) = e ^ {-j \ omega t}}

, gdzie

{\ Displaystyle \ omega > 0}

.

Następnie:

{\ Displaystyle {\begin{wyrównane}{\kapelusz {s}}(t)&=je^{-j\omega t},\\s_{\mathrm {a}}(t)&=e^{-j\omega t}+j^{2}e^{-j\omega t}=e^{-j\omega t}-e^{-j\omega t}=0.\end{wyrównane}}}

Nieruchomości

Chwilowa amplituda i faza

Funkcja na niebiesko i wielkość jej analitycznej reprezentacji na czerwono, pokazująca efekt obwiedni.

Sygnał analityczny można również wyrazić we współrzędnych biegunowych :

{\ Displaystyle s _ {\ operatorname {a}} (t) = s _ {\ operatorname {m}} (t) e ^ {j \ fi (T)},}

gdzie wprowadza się następujące wielkości zmienne w czasie:

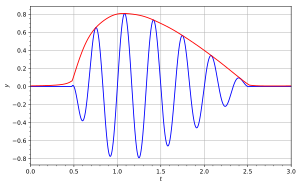
${\ Displaystyle s _ {\ operatorname {m}} (t) \ triangleq | s _ {\ operatorname {a}} (t) |}$ nazywa się chwilową amplitudą lub obwiednią ;
${\ Displaystyle \ phi (t) \ trójkątq \ arg \! \ lewo [s _ {\ operatorname {a}} (t) \ prawej]}$ nazywana jest fazą chwilową lub kąt fazowy .

Na załączonym diagramie niebieska krzywa $_ {\ operatorname {m}} (t$ ( $s$ .

Pochodna czasowa nieopakowanej fazy chwilowej ma jednostki radianów/sekundę i jest nazywana chwilową częstotliwością kątową :

{\ Displaystyle \ omega (t) \ trójkąt q {\ Frac {d \ phi} {dt}} (t).}

Chwilowa częstotliwość (w hercach ) wynosi zatem:

{\ Displaystyle f (t) \ trójkąt q {\ Frac {1} {2 \ pi}} \ omega (t).}

Chwilowa amplituda, chwilowa faza i częstotliwość są w niektórych zastosowaniach używane do pomiaru i wykrywania lokalnych cech sygnału. Inne zastosowanie analitycznej reprezentacji sygnału dotyczy demodulacji modulowanych sygnałów . Współrzędne biegunowe wygodnie oddzielają efekty modulacji amplitudy i modulacji fazy (lub częstotliwości) oraz skutecznie demodulują niektóre rodzaje sygnałów.

Złożona koperta/pasmo podstawowe

Sygnały analityczne są często przesuwane pod względem częstotliwości (konwertowane w dół) w kierunku 0 Hz, prawdopodobnie tworząc [niesymetryczne] ujemne składowe częstotliwości:

{\ Displaystyle {s_ {\ operatorname {a}}} _ { \downarrow }(t)\triangleq s_{\mathrm {a} }(t)e^{-j\omega _{0}t}=s_{\mathrm {m} }(t)e^{j(\ phi (t)-\omega _{0}t)},}

gdzie

.

dowolną referencyjną częstotliwością kątową

Ta funkcja występuje pod różnymi nazwami, takimi jak złożona obwiednia i zespolone pasmo podstawowe . Złożona koperta nie jest wyjątkowa; jest to określone przez wybór ${\ displaystyle \ omega _ {0}}$ . Ta koncepcja jest często używana w przypadku sygnałów pasma przepustowego . Jeśli jest $sygnałem$ , $nośną$ zrównać z .

W innych przypadkach jest wybierany $tak,$ znajdował się gdzieś pośrodku pożądanego pasma przepustowego. Następnie prosty filtr dolnoprzepustowy z rzeczywistymi współczynnikami może wyciąć część zainteresowania. Innym motywem jest zmniejszenie najwyższej częstotliwości, co zmniejsza minimalną częstotliwość próbkowania bez aliasów. Przesunięcie częstotliwości nie podważa matematycznej wykonalności złożonej reprezentacji sygnału. W tym sensie sygnał poddany konwersji w dół jest nadal analityczny . Jednak przywrócenie reprezentacji o wartościach rzeczywistych nie jest już prostą kwestią wyodrębnienia rzeczywistego składnika. Może być wymagana konwersja w górę, a jeśli sygnał był próbkowany (w czasie dyskretnym), interpolacja ( próbkowanie w górę ) może być również konieczna, aby uniknąć aliasingu .

Jeśli zostanie wybrana większa niż najwyższa częstotliwość ${\ Displaystyle s _ {\ operatorname {a}} (t)$ $t$ to ${s_{\mathrm {a}}}_{\downarrow}(t)$ nie ma dodatnich częstotliwości. W takim przypadku wyodrębnienie rzeczywistego komponentu przywraca je, ale w odwrotnej kolejności; składowe o niskiej częstotliwości są teraz składnikami o wysokiej częstotliwości i odwrotnie. Można to wykorzystać do demodulowania typu jednowstęgowego zwanego dolnym wstęgą boczną lub odwróconą wstęgą boczną .

Czasami rozważane są inne wybory częstotliwości odniesienia:

Czasami wybiera $minimalizację$ ${\ Displaystyle \ int _ {0} ^ {+ \ infty} (\ omega - \ omega _ {0}) ^ {2} | S _ {\ operatorname {a}} (\ omega) | ^ {2} \, d\ omega .}$
Alternatywnie, ${0}$ wybrać, aby zminimalizować błąd średniokwadratowy w liniowym przybliżeniu nieopakowanej fazy chwilowej ${\ Displaystyle \ phi (t)}: ω {\ Displaystyle \ omega _$ } ${\ Displaystyle \ int _ {- \ infty} ^ {+ \ infty} [\ omega (t) - \ omega _ {0}] ^ {2} | s _ {\ operatorname {a}} (t) |^{2}\,dt}$
lub inna alternatywa (dla jakiegoś optymalnego) : ${\ displaystyle \ theta}$ ${\ Displaystyle \ int _ {- \ infty} ^ {+ \ infty} [\ phi (t) - (\ omega _ {0} t + \ theta)] ^ {2} \, dt.}$

W dziedzinie przetwarzania sygnałów czasowo-częstotliwościowych wykazano, że sygnał analityczny był potrzebny do zdefiniowania rozkładu Wignera-Ville'a, aby metoda mogła mieć pożądane właściwości potrzebne do praktycznych zastosowań.

Czasami wyrażeniu „złożona obwiednia” nadaje się prostsze znaczenie złożonej amplitudy wskazu (o stałej częstotliwości); innym razem $zdefiniowano$ obwiednia złożonej amplitudy. Ich związek nie różni się od tego w przypadku wartości rzeczywistych: zmieniająca się obwiednia uogólniająca stałą amplitudę .

Rozszerzenia sygnału analitycznego na sygnały wielu zmiennych

Pojęcie sygnału analitycznego jest dobrze zdefiniowane dla sygnałów jednej zmiennej, którą zazwyczaj jest czas. W przypadku sygnałów o dwóch lub więcej zmiennych sygnał analityczny można zdefiniować na różne sposoby, a poniżej przedstawiono dwa podejścia.

Wielowymiarowy sygnał analityczny oparty na kierunku ad hoc

Proste uogólnienie sygnału analitycznego można przeprowadzić dla sygnału wielowymiarowego po ustaleniu, co oznaczają w tym przypadku częstotliwości ujemne . Można to zrobić, wprowadzając $wektor$ jednostkowy w domenie Fouriera i oznaczając dowolny $.$ ujemny jeśli ${\ Displaystyle {\ boldsymbol {\ xi}} \ cdot {\ boldsymbol {\ kapelusz {u}} <0}$ . Sygnał analityczny jest następnie generowany przez usunięcie wszystkich częstotliwości ujemnych i pomnożenie wyniku przez 2, zgodnie z procedurą opisaną dla sygnałów o jednej zmiennej. Jednak nie ma określonego kierunku $który należy wybrać, chyba$ istnieją dodatkowe ograniczenia. Dlatego wybór $.$ lub specyficzny dla aplikacji

Sygnał monogeniczny

Część rzeczywista i urojona sygnału analitycznego odpowiadają dwóm elementom sygnału monogenicznego o wartościach wektorowych, tak jak jest to zdefiniowane dla sygnałów z jedną zmienną. Jednak sygnał monogeniczny można rozszerzyć na dowolną liczbę zmiennych w prosty sposób, tworząc ( n + 1) -wymiarową funkcję o wartościach wektorowych dla przypadku n -zmiennych sygnałów.

Zobacz też

Aplikacje

Notatki

Dalsza lektura

Leon Cohen, Analiza czasowo-częstotliwościowa , Prentice Hall, Upper Saddle River, 1995.
Frederick W. King, Transformacje Hilberta , tom. II, Cambridge University Press, Cambridge, 2009.
B. Boashash, Analiza i przetwarzanie sygnału czasowo-częstotliwościowego: kompleksowe źródło informacji , Elsevier Science, Oxford, 2003.

Linki zewnętrzne

Sygnały analityczne i filtry z transformacją Hilberta