Dyfrakcja włókien

Dyfrakcja światłowodowa to podobszar rozpraszania , obszar, w którym struktura molekularna jest określana na podstawie danych rozpraszania (zwykle promieni rentgenowskich, elektronów lub neutronów). W dyfrakcji światłowodowej wzór rozpraszania nie zmienia się, ponieważ próbka jest obracana wokół unikalnej osi (osi światłowodu). makrocząsteczek biologicznych lub stworzonych przez człowieka . W krystalografii symetria włókien jest utrudnieniem w określaniu struktury krystalicznej, ponieważ refleksy są rozmyte i mogą nakładać się na obraz dyfrakcyjny włókien. Materiałoznawstwo uważa symetrię włókien za uproszczenie, ponieważ prawie wszystkie możliwe do uzyskania informacje o strukturze znajdują się w pojedynczym dwuwymiarowym (2D) wzorze dyfrakcyjnym naświetlonym na kliszy fotograficznej lub detektorze 2D. Do opisania dyfrakcji światłowodu wystarczą 2 zamiast 3 współrzędnych kierunków.

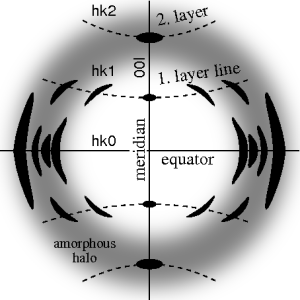
Idealny wzór dyfrakcji włókien półkrystalicznego materiału z amorficznym halo i refleksami na liniach warstw. Wysoka intensywność jest reprezentowana przez ciemny kolor. Oś włókna jest pionowa

Idealny układ włókien wykazuje symetrię 4-ćwiartkową . W układzie idealnym oś włókna nazywana jest południkiem , kierunek prostopadły nazywany jest równikiem . W przypadku symetrii światłowodu we wzorze 2D pojawia się znacznie więcej odbić niż w przypadku dyfrakcji monokrystalicznej. We wzorach włókien te refleksy wyraźnie pojawiają się ułożone wzdłuż linii ( linii warstwowych ) biegnących prawie równolegle do równika. Tak więc w dyfrakcji światłowodowej koncepcja linii warstw krystalografii staje się namacalna. Zagięte linie warstw wskazują, że wzór musi zostać wyprostowany. Refleksje są oznaczone indeksem Millera hkl, czyli 3 cyfry. Refleksje na i -tej warstwy mają udział l= i . Refleksje na południku to refleksy 00l. W krystalografii wzory dyfrakcyjne włókien sztucznych są generowane przez obracanie pojedynczego kryształu wokół osi ( metoda obracającego się kryształu ).

W eksperymentach uzyskuje się nieidealne wzory włókien. Pokazują tylko lustrzaną symetrię wokół południka. Powodem jest to, że oś światłowodu i padająca wiązka (promienie rentgenowskie, elektrony, neutrony) nie mogą być idealnie zorientowane prostopadle względem siebie. Odpowiednie zniekształcenie geometryczne zostało obszernie zbadane przez Michaela Polanyiego , wprowadzając koncepcję kuli Polanyi'ego (niem. „Lagenkugel”) przecinającej sferę Ewalda . Później Rosalind Franklin i Raymond Gosling przeprowadzili własne rozumowanie geometryczne i przedstawili przybliżone równanie kąta nachylenia włókna β. Analiza rozpoczyna się od odwzorowania zniekształconego wzoru 2D na reprezentatywnej płaszczyźnie światłowodu. Jest to płaszczyzna, która zawiera oś walca w odwrotnej przestrzeni . W krystalografii najpierw oblicza się przybliżenie odwzorowania na odwrotność przestrzeni , które jest udoskonalane iteracyjnie. Metoda cyfrowa często nazywana korektą Frasera zaczyna się od przybliżenia Franklina dla kąta nachylenia β. Eliminuje pochylenie światłowodu, odkształca obraz detektora i koryguje intensywność rozpraszania. Prawidłowe równanie do wyznaczania β przedstawił Norbert Stribeck.

Rola historyczna

Materiały włókniste, takie jak wełna lub bawełna, łatwo tworzą wyrównane wiązki i były jednymi z pierwszych makrocząsteczek biologicznych badanych za pomocą dyfrakcji rentgenowskiej, zwłaszcza przez Williama Astbury'ego na początku lat trzydziestych XX wieku. Dane z dyfrakcji światłowodowej doprowadziły do ​​kilku ważnych postępów w rozwoju biologii strukturalnej , np. oryginalnych modeli helisy α i modelu dwuniciowego DNA Watsona-Cricka .

Geometria dyfrakcji światłowodu

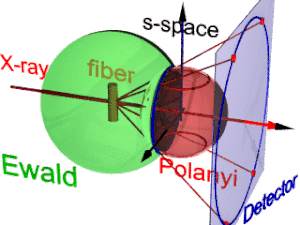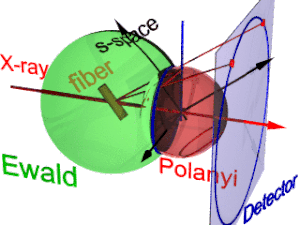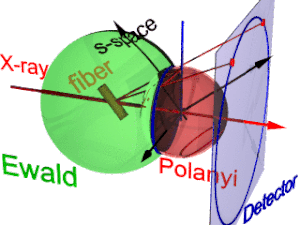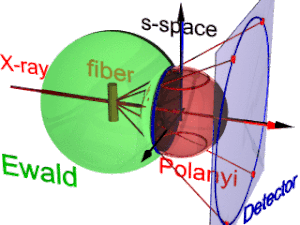
Geometria dyfrakcji światłowodu zmienia się, gdy światłowód jest pochylany (kąt nachylenia β znajduje się między niebieską osią sztywną a osią oznaczoną jako s-space ). Informacja o strukturze znajduje się w przestrzeni odwrotności (czarne osie), rozciągnięta na powierzchnie sfer Polanyi'ego. W animacji monitorowana jest 1 kula Polanyiego z 1 odbiciem na niej

Animacja przedstawia geometrię dyfrakcji światłowodu. Opiera się na pojęciach zaproponowanych przez Polanyiego. Kierunek odniesienia to wiązka główna (etykieta: X-ray). Jeżeli włókno jest odchylone od kierunku prostopadłego o kąt β, to również informacja o jego budowie molekularnej w przestrzeni odwrotności (trójścian oznaczony jako s-space ) jest nachylona. W przestrzeni odwrotnej kula Ewalda ma swój środek w próbce. Jego promień wynosi 1/λ, gdzie λ to długość fali padającego promieniowania. Na powierzchni kuli Ewalda znajdują się wszystkie punkty przestrzeni odwrotnej, które widzi detektor. Punkty te są odwzorowywane na pikselach detektora przez projekcję centralną.

W przestrzeni s każde odbicie znajduje się na swojej sferze Polanyi'ego. Wewnętrznie idealnym odbiciem jest punkt w przestrzeni s, ale symetria włókna zamienia go w pierścień rozmazany przez obrót wokół kierunku włókna. Dwa pierścienie reprezentują każde odbicie na sferze Polanyi'ego, ponieważ rozpraszanie jest punktowo symetryczne względem początku s-przestrzeni. Na detektor odwzorowywane są tylko te punkty odbicia w przestrzeni s, które znajdują się zarówno na sferze Ewalda , jak i na sferze Polanyi'ego. Punkty te tworzą okrąg refleksyjny (niebieski pierścień). Nie zmienia się, gdy włókno jest pochylane. Podobnie jak w przypadku rzutnika slajdów, na detektorze ( koło detektora , niebieski pierścień) rzutowany jest odblaskowy krąg (czerwone poruszające się promienie). Mogą pojawić się do 4 obrazów (czerwone punkty) monitorowanego odbicia. Położenie obrazów refleksyjnych jest funkcją orientacji włókna w wiązce pierwotnej ( równanie Polanyiego ). Odwrócony , obrazów refleksyjnych można określić orientację włókna, jeśli dla Millera i jest ważny. Z reprezentacji geometrii dyfrakcyjnej włókien Polanyi'ego relacje mapowania włókien są ustalane przez elementarną i sferyczną.

Korekta wzoru

Zmierzony wzór włókien
Wzór włókien polipropylenu odwzorowany na (reprezentatywną płaszczyznę) przestrzeni odwrotnej

Rysunek po lewej pokazuje typowy wzór włókien polipropylenu przed odwzorowaniem go na odwrotną przestrzeń. Oś lustra we wzorze jest obrócona o kąt stosunku do kierunku pionowego Wadę tę rekompensuje proste obracanie obrazu. 4 proste strzałki wskazują 4 obrazy odbicia wybranego odbicia referencyjnego. Ich pozycje są wykorzystywane do określenia kąta nachylenia włókna . Obraz zarejestrowano na detektorze CCD. Pokazuje logarytmiczną intensywność w reprezentacji pseudokolorów. Tutaj jasne kolory reprezentują wysoką intensywność.

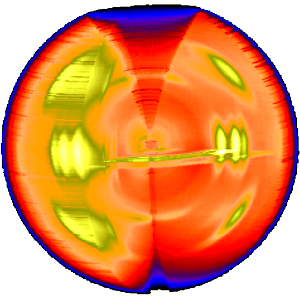
Po określeniu odległości między a detektorem oblicza się przy użyciu znanych danych krystalograficznych odbicia odniesienia, konstruuje się mapę z jednolitą siatką dla reprezentatywnej płaszczyzny włókna w przestrzeni odwrotnej i dane dyfrakcyjne są wprowadzane do tej mapy . Rysunek po prawej pokazuje wynik. Zmiana intensywności rozpraszania została uwzględniona w procesie unwarpingu. Ze względu na krzywiznę powierzchni kuli Ewalda na południku pozostają białe plamy, w których brakuje informacji o strukturze. Tylko w środku obrazu i przy wartości s związanej z kątem rozproszenia informacje o strukturze południka Oczywiście, istnieje teraz symetria 4-kwadrantowa. Oznacza to, że w przykładowym wzorze część brakujących informacji może zostać skopiowana „z dolnej połowy do górnej połowy” na białe obszary. Dlatego często sensowne jest celowe nachylenie włókna.

Reprezentacja 3D przestrzeni odwrotności wypełnionej danymi rozpraszania z włókna polipropylenowego

Trójwymiarowy szkic pokazuje, że w przykładowym eksperymencie zebrane informacje na temat struktury molekularnej włókna polipropylenowego są prawie kompletne. Dzięki obrotowi wzoru płaszczyzny wokół południka dane rozpraszania zebrane w ciągu 4 s wypełniają prawie sferyczną objętość s-przestrzeni. W przykładzie symetria 4-kwadrantowa nie została jeszcze uznana za wypełniającą część białych plam. Dla jasności wycięto ćwiartkę kuli, ale z zachowaniem samej płaszczyzny równikowej.

  • Arnott S & Wonacott AJ, The Refinement of the Molecular & Crystal Structures of Polymers using X-Ray Data and Stereochemical Constraints, Polymer 1966 7 157 - 166
  • Bian W, Wang H, McCullogh I, Stubbs G (2006). „WCEN: program komputerowy do wstępnego przetwarzania wzorów dyfrakcji włókien”. J. Appl. krystalograf. , 39 , 752-756.
  • Bunn CW, Chemical Crystallography, University of Oxford, wyd. 2, 1967
  • Campbell Smith PJ & Arnott S, LALS (itp.) Acta Crystallogr 1978 A34 3 - 11
  • Cochran W, Crick FHC i Vand V (1952). „Struktura syntetycznych polipeptydów. I. Transformacja atomów na helisie”. Acta Crystallogr. , 5 , 581-586.
  • Donohue J i Trueblood, KN, O zawodności wskaźnika niezawodności, Acta Crystallogr, 1956, 9 , 615
  • Franklin RE, Gosling RG (1953) „Struktura włókien tymojądrowych sodu. II. Cylindrycznie symetryczna funkcja Pattersona”. Acta Crystallogr. , 6 , 678-685
  • Fraser RDB, Macrae TP, Miller A, Rowlands RJ (1976). „Cyfrowe przetwarzanie wzorów dyfrakcji włókien”. J. Appl. krystalograf. , 9 , 81-94.
  • Hamilton WC, R-Factors, Statistics and Truth, Paper H5, Amer Cryst Ass Program & Abstracts, Boulder, Colorado, 1961
  • Hamilton WC, Testy istotności na krystalograficznym współczynniku R, Acta Crystallogr 1965 18 502 - 510
  • James TW & Mazia D, Folie powierzchniowe kwasu dezoksyrybonukleinowego, Biochim Biophys Acta 1953 10 367 - 370
  • Marvin DA (2017) „Badania dyfrakcyjne włókien biologicznych makrocząsteczek”. Wałówka. Biofiza. Mol. Biol. 127 , 43-87.
  • Millane RP, Arnott S (1985) „Cyfrowe przetwarzanie wzorów dyfrakcji rentgenowskiej z włókien zorientowanych”. J. Macromol. nauka fizyka , B24 , 193-227
  • Polanyi M (1921) „Das Röntgen-Faserdiagramm (Erste Mitteilung)”. Z. Physik , 7 , 149-180
  • Polanyi M, Weissenberg K (1923) „Das Röntgen-Faserdiagramm (Zweite Mitteilung)”. Z. Physik , 9 , 123-130
  • Rajkumar G, AL-Khayat H, Eakins F, He A, Knupp C, Squire J (2005) „FibreFix — nowy zintegrowany pakiet oprogramowania CCP13”, Fiber Diffraction Rev. , 13 , 11-18
  • Stribeck N. (2009). „O wyznaczaniu kątów nachylenia włókien w dyfrakcji włókien” Acta Crystallogr. , A65 , 46-47

Książki tekstowe

Linki zewnętrzne

  • WCEN — Oprogramowanie (Linux, Mac, Windows) do analizy rozkładu włókien
  • Fibre Diffraction — wprowadzenie prof. KC Holmesa z Instytutu Badań Medycznych im. Maxa Plancka w Heidelbergu.
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Fiber_diffraction&oldid=1096845657 ”