Równia pochyła

„Rampa” przekierowuje tutaj. W przypadku innych zastosowań zobacz Rampa (ujednoznacznienie) .

Ten artykuł dotyczy struktury fizycznej. W przypadku innych zastosowań zobacz Płaszczyzna nachylona (ujednoznacznienie) .

Rampa dla wózków inwalidzkich , Hotel Montescot, Chartres, Francja

Demonstracyjna pochylona płaszczyzna używana w edukacji, Museo Galileo , Florencja.

Nachylona płaszczyzna , znana również jako rampa , jest płaską powierzchnią nośną nachyloną pod kątem od kierunku pionowego , z jednym końcem wyższym niż drugi, służącą jako pomoc do podnoszenia lub opuszczania ładunku. Nachylona płaszczyzna jest jedną z sześciu klasycznych prostych maszyn zdefiniowanych przez renesansowych naukowców. Pochyłe płaszczyzny służą do przemieszczania ciężkich ładunków nad pionowymi przeszkodami. Przykłady obejmują rampę używaną do załadunku towarów na ciężarówkę, osobę idącą po rampie dla pieszych, samochód lub pociąg kolejowy wjeżdżający na wzniesienie.

Przesunięcie przedmiotu w górę po pochyłej płaszczyźnie wymaga mniejszej siły niż podniesienie go prosto w górę, kosztem zwiększenia przebytej odległości. Mechaniczna zaleta pochyłej płaszczyzny, współczynnik zmniejszający siłę, jest równa stosunkowi długości nachylonej powierzchni do wysokości, na której się ona znajduje. Z zasady zachowania energii wynika, że ​​do podniesienia danego przedmiotu na określoną odległość w pionie potrzebna jest ta sama ilość energii mechanicznej ( pracy ) , pomijając straty spowodowane tarciem . , ale nachylona płaszczyzna umożliwia wykonanie tej samej pracy z mniejszą siłą wywieraną na większą odległość.

Kąt tarcia , zwany także czasem kątem spoczynku , to maksymalny kąt, pod którym ładunek może spoczywać nieruchomo na pochyłej płaszczyźnie w wyniku tarcia bez zsuwania się. μs _Kąt ten jest równy arcus tangensowi współczynnika tarcia statycznego między powierzchniami.

Często uważa się, że dwie inne proste maszyny wywodzą się z pochyłej płaszczyzny. Klin za ruchomą pochyloną płaszczyznę lub dwie pochylone płaszczyzny połączone u podstawy. Śruba składa się z wąskiej nachylonej płaszczyzny owiniętej wokół cylindra .

Termin ten może również odnosić się do konkretnej implementacji; prosta rampa wcięta w strome zbocze do transportu towarów w górę iw dół wzgórza. Może to obejmować samochody na szynach lub ciągnięte przez system linowy; kolejka linowa lub linowa , taka jak pochyła płaszczyzna Johnstown .

Używa

Nachylenia są szeroko stosowane w postaci ramp załadunkowych do załadunku i rozładunku towarów na samochody ciężarowe, statki i samoloty. Podjazdy dla wózków inwalidzkich służą osobom poruszającym się na wózkach inwalidzkich do pokonywania pionowych przeszkód bez przekraczania ich sił. Schody ruchome i pochylone przenośniki taśmowe są również formami pochyłej płaszczyzny. W kolejce linowej lub kolejce linowej wagon kolejowy jest wciągany po stromej pochyłości za pomocą lin. Nachylone samoloty umożliwiają również bezpieczne opuszczanie ciężkich, delikatnych przedmiotów, w tym ludzi, na odległość pionową, przy użyciu normalnej siły samolotu w celu zmniejszenia siły grawitacji . Zjeżdżalnie ewakuacyjne z samolotów umożliwiają szybkie i bezpieczne zejście na ziemię z wysokości samolotu pasażerskiego .

Używanie ramp do załadunku samochodu na ciężarówkę

Załadunek ciężarówki na statek za pomocą rampy

Zjeżdżalnia ewakuacyjna samolotu

Rampa dla wózków inwalidzkich w japońskim autobusie

Rampa załadunkowa na ciężarówkę

Inne pochyłe płaszczyzny są wbudowane w trwałe konstrukcje. Drogi dla pojazdów i kolei mają pochyłe płaszczyzny w postaci stopniowych zboczy, ramp i grobli , aby umożliwić pojazdom pokonywanie pionowych przeszkód, takich jak wzniesienia, bez utraty przyczepności na powierzchni drogi. Podobnie ścieżki i chodniki dla pieszych mają łagodne rampy ograniczające ich nachylenie, aby zapewnić pieszym utrzymanie przyczepności. Samoloty pochyłe są również wykorzystywane jako rozrywka dla ludzi do zjeżdżania w kontrolowany sposób, na zjeżdżalniach na placach zabaw , zjeżdżalniach wodnych , stokach narciarskich i parki deskorolkowe .

Ziemna rampa (po prawej) zbudowana przez Rzymian w 72 rne w celu inwazji na Masadę w Izraelu

Rampa dla pieszych, Palacio do Planalto, Brasilia

Pochylona płaszczyzna Johnstown , kolejka linowo -terenowa .

Birma Road, Assam, Indie, przez Birmę do Chin, ok. 1945

Pochylone samoloty w parku deskorolkowym

Historia

Dowód Stevina

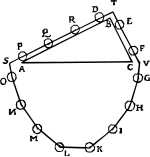
W 1586 roku flamandzki inżynier Simon Stevin (Stevinus) wyprowadził mechaniczną przewagę pochyłej płaszczyzny na podstawie argumentu wykorzystującego sznur koralików. Wyobraził sobie dwie nachylone płaszczyzny o równej wysokości, ale różnych nachyleniach, umieszczone tyłem do siebie (powyżej) jak w pryzmacie. Pętla sznurka z koralikami w równych odstępach jest udrapowana na nachylonych płaszczyznach, z częścią sznurka zwisającą poniżej. Koraliki spoczywające na płaszczyznach działają jak obciążenia na płaszczyznach, utrzymywane przez siłę naciągu sznurka w punkcie T . Argument Stevina wygląda następująco: Struna musi być nieruchoma, w równowadze statycznej . Gdyby sznurek był cięższy z jednej strony niż z drugiej i zaczął się ślizgać w prawo lub w lewo pod własnym ciężarem, to kiedy każdy koralik przesunąłby się do pozycji poprzedniego koralika, sznurek byłby nie do odróżnienia od swojego początkowego położenia i dlatego nadal by się poruszał. być niezrównoważony i ślizgać się. Argument ten można powtarzać w nieskończoność, co prowadzi do kołowego perpetuum mobile , co jest absurdem. Dlatego jest nieruchomy, a siły po obu stronach w punkcie T ( powyżej ) są równe. Część łańcucha zwisająca poniżej nachylonych płaszczyzn jest symetryczna, z równą liczbą koralików po każdej stronie. Wywiera jednakową siłę na każdą stronę struny. Dlatego ta część sznurka może zostać odcięta na krawędziach płaszczyzn (punkty S i V) , pozostawiając jedynie koraliki spoczywające na nachylonych płaszczyznach, a ta pozostała część nadal będzie w równowadze statycznej. Ponieważ koraliki są rozmieszczone na sznurku w równych odstępach, całkowita liczba koralików podtrzymywanych przez każdą płaszczyznę, czyli całkowite obciążenie, jest proporcjonalna do długości płaszczyzny. Ponieważ wejściowa siła podtrzymująca, naprężenie struny, jest taka sama dla obu, przewaga mechaniczna każdej płaszczyzny jest proporcjonalna do jej długości po skosie Jak zauważył Dijksterhuis, argument Stevina nie jest całkowicie ścisły. Siły wywierane przez wiszącą część łańcucha nie muszą być symetryczne, ponieważ wisząca część nie musi zachowywać swojego kształtu po puszczeniu. Nawet jeśli łańcuch zostanie uwolniony z zerowym momentem pędu, ruch obejmujący oscylacje jest możliwy, chyba że łańcuch jest początkowo w konfiguracji równowagi, przypuszczenie, które uczyniłoby argument okrągłym.

Samoloty pochyłe były używane przez ludzi od czasów prehistorycznych do przenoszenia ciężkich przedmiotów. Pochyłe drogi i groble zbudowane przez starożytne cywilizacje, takie jak Rzymianie, są przykładami wczesnych pochyłych płaszczyzn, które przetrwały i pokazują, że rozumieli wartość tego urządzenia do przenoszenia rzeczy pod górę. Uważa się , że ciężkie kamienie używane w starożytnych konstrukcjach kamiennych, takich jak Stonehenge , zostały przesunięte i ustawione na miejscu za pomocą pochyłych płaszczyzn wykonanych z ziemi, chociaż trudno jest znaleźć dowody na istnienie takich tymczasowych ramp budowlanych. Piramidy egipskie zostały zbudowane przy użyciu pochyłych płaszczyzn, Siege rampy umożliwiały starożytnym armiom pokonywanie murów twierdzy. Starożytni Grecy zbudowali brukowaną rampę o długości 6 km (3,7 mil), Diolkos , aby przeciągać statki drogą lądową przez Przesmyk Koryncki .

Jednak pochylona płaszczyzna była ostatnią z sześciu klasycznych prostych maszyn , które zostały rozpoznane jako maszyna. Dzieje się tak prawdopodobnie dlatego, że jest to urządzenie bierne i nieruchome (część ruchoma jest ładunkiem), a także dlatego, że występuje w naturze w postaci zboczy i pagórków. starożytni filozofowie greccy , którzy rozumieli jego zastosowanie do podnoszenia ciężkich przedmiotów, zdefiniowali pozostałe pięć prostych maszyn, nie uwzględnili pochylonej płaszczyzny jako maszyny. Pogląd ten utrzymywał się wśród kilku późniejszych naukowców; dopiero w 1826 roku Karl von Langsdorf pisał, że płaszczyzna pochyła " ... nie jest bardziej maszyną niż zbocze góry ”. Problem obliczenia siły potrzebnej do wepchnięcia ciężaru na pochyłą płaszczyznę (jego zaleta mechaniczna) został podjęty przez greckich filozofów Heron z Aleksandrii (ok. 10 - 60 n.e.) i Pappus z Aleksandrii (ok. 290 - 350 n.e.), ale ich rozwiązania były błędne.

Dopiero w renesansie pochyła płaszczyzna została rozwiązana matematycznie i sklasyfikowana wraz z innymi prostymi maszynami. Pierwsza poprawna analiza płaszczyzny nachylonej pojawiła się w dziele XIII-wiecznego autora Jordanusa de Nemore , jednak jego rozwiązanie najwyraźniej nie zostało przekazane innym ówczesnym filozofom. Girolamo Cardano (1570) zaproponował błędne rozwiązanie, zgodnie z którym siła wejściowa jest proporcjonalna do kąta płaszczyzny. Następnie pod koniec XVI wieku trzy poprawne rozwiązania zostały opublikowane w ciągu dziesięciu lat przez Michaela Varro (1584), Simona Stevina (1586) i Galileo Galilei (1592). Chociaż nie był to pierwszy, wyprowadzenie flamandzkiego inżyniera Simona Stevina jest najbardziej znane ze względu na swoją oryginalność i użycie sznurka paciorków (patrz ramka). W 1600 roku włoski naukowiec Galileo Galilei włączył nachyloną płaszczyznę do swojej analizy prostych maszyn w Le Meccaniche („O mechanice”), pokazując jej podstawowe podobieństwo do innych maszyn jako wzmacniacza siły.

Pierwsze elementarne zasady tarcia ślizgowego na pochyłej płaszczyźnie zostały odkryte przez Leonarda da Vinci (1452-1519), ale nie zostały opublikowane w jego notatnikach. Zostały ponownie odkryte przez Guillaume'a Amontonsa (1699) i dalej rozwinięte przez Charlesa-Augustina de Coulomba (1785). Leonhard Euler (1750) wykazał, że tangens kąta spoczynku na płaszczyźnie pochyłej jest równy współczynnikowi tarcia .

Terminologia

Nachylenie

Mechaniczna zaleta pochyłej płaszczyzny zależy od jej nachylenia , co oznacza jej nachylenie lub stromość. Im mniejsze nachylenie, tym większa przewaga mechaniczna i mniejsza siła potrzebna do podniesienia danego ciężaru. Nachylenie płaszczyzny s jest równe różnicy wysokości między jej dwoma końcami, czyli „ wzniesieniu ”, podzielonej przez jej długość poziomą, czyli „ bieg ”. Można to również wyrazić przez kąt, jaki płaszczyzna tworzy z poziomem, θ .

Geometria pochylonej płaszczyzny oparta jest na trójkącie prostokątnym . Pozioma długość jest czasami nazywana Run , pionowa zmiana wysokości Rise .

${\ Displaystyle \ teta = \ tan ^ {- 1} {\ bigg (} {\ Frac {\ text {Rise}} {\ text {Run}}} {\ bigg) }\,}$

Przewaga mechaniczna

Przewaga mechaniczna MA prostej maszyny jest zdefiniowana jako stosunek siły wyjściowej wywieranej na ładunek do przyłożonej siły wejściowej. Dla płaszczyzny nachylonej wyjściowa siła obciążenia jest po prostu siłą grawitacji obiektu obciążenia na płaszczyźnie, jego _ciężarem Fw . Siła wejściowa to siła F _i wywierana na obiekt równolegle do płaszczyzny, aby przesunąć go w górę płaszczyzny. Zaletą mechaniczną jest

${\ Displaystyle \ operatorname {MA} = {\ Frac {F_ {w}} {F_ {i}}} \,}$

MA idealnej nachylonej płaszczyzny bez tarcia jest czasami nazywana idealną przewagą mechaniczną (IMA), podczas gdy MA z uwzględnieniem tarcia nazywana jest rzeczywistą przewagą mechaniczną (AMA).

Pochyła płaszczyzna bez tarcia

Oprzyrządowana pochyła płaszczyzna używana do nauczania fizyki, około 1900 r. Ciężarek po lewej stronie zapewnia siłę _obciążenia Fw . Prawy ciężarek zapewnia siłę wejściową F _i ciągnącą walec w górę płaszczyzny.

Jeśli nie ma tarcia między poruszanym przedmiotem a płaszczyzną, urządzenie nazywa się idealną płaszczyzną nachyloną . Ten warunek można osiągnąć, jeśli obiekt toczy się jak beczka lub jest wsparty na kółkach lub kółkach . Ze względu na zasadę zachowania energii dla pochyłej płaszczyzny pozbawionej tarcia praca wykonana przy podnoszeniu ciężaru W _out jest równa pracy wykonanej przez siłę wejściową W _in

${\ Displaystyle W _ {\ rm {na zewnątrz}} = W _ {\ rm {w}} \,}$

Pracę definiuje się jako siłę pomnożoną przez przemieszczenie, o które porusza się obiekt. Praca wykonana nad ładunkiem jest równa jego ciężarowi pomnożonemu przez pionowe przemieszczenie, które podnosi, co jest „podnoszeniem się” płaszczyzny nachylonej

${\ Displaystyle W _ {\ rm {na zewnątrz}} = F_ {w} \ cdot {\ tekst {wzrost}} \,}$

Praca wejściowa jest równa sile F _i działającej na obiekt pomnożonej przez długość przekątnej nachylonej płaszczyzny.

${\ Displaystyle W _ {\ rm {w}} = F_ {i} \ cdot {\ tekst {długość}} \,}$

Podstawienie tych wartości do powyższego równania zachowania energii i przekształcenie

${\ Displaystyle {\ tekst {MA}} = {\ Frac {F_ {w}} {F_ {i}}} = {\ Frac {\ tekst {długość}}} {\ tekst {Wzrastać}}}\,}$

Aby wyrazić przewagę mechaniczną przez kąt θ płaszczyzny, z diagramu (powyżej) widać, że

${\ Displaystyle \ sin \ theta = {\ Frac {\ tekst {wzrost}} {\ tekst {długość}}} \,}$

Więc

${\ Displaystyle {\ tekst {MA}} = {\ Frac {F_ {w}} {F_ {i}}} = {\ Frac {1} {\ sin \ teta }}\,}$

Tak więc mechaniczna przewaga pochyłej płaszczyzny bez tarcia jest równa odwrotności sinusa kąta nachylenia. Siła wejściowa F _i z tego równania jest siłą potrzebną do utrzymania ładunku w bezruchu na pochyłej płaszczyźnie lub wypchnięcia go w górę ze stałą prędkością. Jeśli siła wejściowa jest większa niż ta, obciążenie przyspieszy w górę płaszczyzny. Jeśli siła jest mniejsza, przyspieszy w dół płaszczyzny.

Płaszczyzna nachylona z tarciem

Tam, gdzie występuje tarcie między płaszczyzną a ładunkiem, jak na przykład podczas wsuwania ciężkiego pudła po rampie, część pracy wykonanej przez siłę wejściową jest rozpraszana w postaci ciepła przez tarcie W tarcie , więc mniej pracy jest _wykonywane na obciążenie. Ze względu na zasadę zachowania energii suma pracy wyjściowej i strat energii tarcia jest równa pracy wejściowej

${\ Displaystyle W _ {\ tekst {w}} = W _ {\ tekst {fric}} + W _ {\ tekst {out}} \,}$

Dlatego wymagana jest większa siła wejściowa, a przewaga mechaniczna jest mniejsza niż w przypadku braku tarcia. W przypadku tarcia ładunek będzie się poruszał tylko wtedy, gdy wypadkowa siła równoległa do powierzchni jest większa niż siła tarcia F _f przeciwstawna. Maksymalna siła tarcia jest dana przez

${\ Displaystyle F_ {f} = \ mu F_ {n} \,}$

gdzie F _n jest siłą normalną między obciążeniem a płaszczyzną skierowaną prostopadle do powierzchni, a μ jest współczynnikiem tarcia statycznego między dwiema powierzchniami, który zmienia się w zależności od materiału. Gdy nie zostanie przyłożona żadna siła, jeśli kąt nachylenia płaszczyzny θ jest mniejszy niż pewna maksymalna wartość φ , składowa siły grawitacji równoległa do płaszczyzny będzie zbyt mała, aby pokonać tarcie, a ładunek pozostanie nieruchomy. Kąt ten nazywany jest kątem spoczynku i zależy od składu powierzchni, ale jest niezależna od ciężaru ładunku. Poniżej pokazano, że tangens kąta spoczynku φ jest równy μ

${\ Displaystyle \ phi = \ tan ^ {- 1} \ mu \,}$

W przypadku tarcia zawsze istnieje pewien zakres siły wejściowej Fi _. , dla której obciążenie jest nieruchome, ani nie przesuwa się w górę ani w dół płaszczyzny, podczas gdy w przypadku płaszczyzny nachylonej bez tarcia istnieje tylko jedna określona wartość siły wejściowej, dla której obciążenie jest nieruchome

Analiza

Legenda: F _n = N = siła normalna prostopadła do płaszczyzny, F _i = f = siła wejściowa, F _w = mg = ciężar ładunku, gdzie m = masa , g = grawitacja

Na ładunek spoczywający na pochyłej płaszczyźnie, rozpatrywany jako ciało swobodne , działają na niego trzy siły:

• Przyłożona siła F _i wywierana na ładunek, aby go przesunąć, która działa równolegle do nachylonej płaszczyzny.
• Ciężar ładunku F _w , który działa pionowo w dół
• Siła samolotu działająca na ładunek. Można to rozłożyć na dwa komponenty:
  • Siła normalna Fn _. nachylonej płaszczyzny działającej na ładunek, podtrzymująca go Jest to skierowane prostopadle ( normalnie ) do powierzchni.
  • Siła tarcia F _f płaszczyzny działającej na ładunek działa równolegle do powierzchni i zawsze ma kierunek przeciwny do ruchu przedmiotu. Jest równa sile normalnej pomnożonej przez współczynnik tarcia statycznego μ między dwiema powierzchniami.

Korzystając z drugiej zasady dynamiki Newtona, ładunek będzie nieruchomy lub w ruchu ustalonym, jeśli suma działających na niego sił wynosi zero. Ponieważ kierunek siły tarcia jest przeciwny w przypadku ruchu w górę iw dół, te dwa przypadki należy rozpatrywać oddzielnie:

• Ruch pod górę: Całkowita siła działająca na ładunek skierowana jest w górę, więc siła tarcia jest skierowana w dół płaszczyzny, przeciwstawiając się sile wejściowej.

Wyprowadzenie przewagi mechanicznej dla ruchu pod górę Równania równowagi dla sił równoległych i prostopadłych do płaszczyzny to ${\ Displaystyle \ suma F_ {\|} = F_ {i} -F_ {f} -F_ {w} \ sin \ teta = 0 \,}$ ${\ Displaystyle \ suma F _ {\ perp} = F_ {n} -F_ {w} \ cos \ teta = 0 \,}$ Podstawiając ${ \displaystyle F_{f}=\mu F_{n}\,}$ do pierwszego równania ${\ Displaystyle F_ {i} -\ mu F_ {n} -F_ {w} \ sin \ theta = 0 \,}$ Rozwiązywanie drugiego równania, aby uzyskać ${\ Displaystyle F_ {n} = F_ {w} \ cos \ theta \,}$ i podstawiając do powyższego równania ${\ Displaystyle F_ {i} - \ mu F_ {w} \ cos \ teta - F_ {w} \ sin \ teta = 0 \,}$ ${ \ Displaystyle {\ Frac {F_ {w}} {F_ {i}}} = {\ Frac {1} {\ sin \ theta + \ mu \ cos \ theta}} \,} Definiowanie$ μ $\ styl wyświetlania \mu =\tan \phi \,}$ ${\ Displaystyle {\ Frac {F_ {w}}} {F_ {i}}} = {\ Frac {1} {\ sin \ theta + \ tan \ phi \ cos \ theta}} = {\ dfrac {1} \sin \theta +{\dfrac {\sin \phi }{\cos \phi }}\cos \theta }}={\frac {\cos \phi }{\sin \theta \cos \phi +\cos \ theta \sin \phi }}\,} Używając$ tożsamości trygonometrycznej sumy kątów w mianowniku,

Zaletą mechaniczną jest

${\ Displaystyle \ operatorname {MA} = {\ Frac {F_ {w}} {F_ {i}}} = {\ frac {\ cos \ phi} {\ sin (\ teta + \ phi)}} \,}$

gdzie ${\ Displaystyle \ phi = \ tan ^ {- 1} \ mu \,}$ . Jest to warunek zbliżającego się ruchu w górę pochyłej płaszczyzny. Jeżeli przyłożona siła F _i jest większy niż podany w tym równaniu, ładunek przesunie się w górę płaszczyzny.

• Ruch w dół: Całkowita siła działająca na ładunek jest skierowana w dół, więc siła tarcia jest skierowana w górę płaszczyzny.

Wyprowadzenie przewagi mechanicznej dla ruchu w dół Równania równowagi są $\ Displaystyle \ suma F_ {\|} = F_ {i} + F_ {f} -F_ {w} \ sin \ teta = 0 \,}$ ${\ Displaystyle \ suma F _ {\ perp} = F_ {n} -F_ {w} \ cos \ theta = 0 \,}$ Podstawiając ${ \displaystyle F_{f}=\mu F_{n}\,}$ do pierwszego równania ${\ Displaystyle F_ {i} + \ mu F_ {n} -F_ {w} \ sin \ theta = 0 \,}$ Rozwiązywanie drugiego równania, aby uzyskać ${\ Displaystyle F_ {n} = F_ {w} \ cos \ theta \,}$ i podstawiając do powyższego równania ${\ Displaystyle F_ {i} + \ mu F_ {w} \ cos \ teta -F_ {w} \ sin \ teta = 0 \,}$ ${ \ Displaystyle {\ Frac {F_ {w}} {F_ {i}}} = {\ Frac {1} {\ sin \ theta - \ mu \ cos \ theta}} \,} Podstawiając$ w ${ \displaystyle \mu =\tan \phi \,}$ i upraszczając jak wyżej ${\ Displaystyle {\ Frac {F_ {w}} {F_ {i}}} = {\ Frac {\ cos \ phi} {\ sin \ teta \ cos \ phi -\cos \theta \sin \phi }}\,}$ Używając innej tożsamości trygonometrycznej w mianowniku,

Zaletą mechaniczną jest

${\ Displaystyle \ operatorname {MA} = {\ Frac {F_ {w}} {F_ {i}}} = {\ frac {\cos \phi }{\sin(\theta -\phi)}}\,}$

Jest to warunek zbliżającego się ruchu w dół płaszczyzny; jeśli przyłożona siła Fi jest mniejsza niż _podana w tym równaniu, obciążenie zsunie się po płaszczyźnie. Istnieją trzy przypadki:

1. ${\ displaystyle \ theta <\ phi \,}$ : przewaga mechaniczna jest ujemna. W przypadku braku przyłożonej siły ładunek pozostanie nieruchomy i wymaga pewnej ujemnej (w dół) przyłożonej siły, aby zsunąć się w dół.
2. ${\ Displaystyle \ theta = \ phi \,}$ : „ kąt spoczynku ”. Przewaga mechaniczna jest nieskończona. Bez przyłożonej siły ładunek nie będzie się przesuwał, ale najmniejsza siła ujemna (w dół) spowoduje jego przesuwanie.
3. ${\ displaystyle \ theta > \ phi \,}$ : przewaga mechaniczna jest pozytywna. W przypadku braku przyłożonej siły ładunek ześlizgnie się po płaszczyźnie i wymaga pewnej siły dodatniej (pod górę), aby utrzymać go w bezruchu

Przewaga mechaniczna przy użyciu mocy

Legenda: N = siła normalna prostopadła do płaszczyzny, W=mg, gdzie m = masa , g = grawitacja , a θ ( theta ) = kąt nachylenia płaszczyzny

Mechaniczną zaletą pochyłej płaszczyzny jest stosunek ciężaru ładunku na rampie do siły potrzebnej do wciągnięcia go na rampę. Jeśli energia nie jest rozpraszana ani magazynowana podczas ruchu ładunku, to tę mechaniczną zaletę można obliczyć na podstawie wymiarów rampy.

Aby to pokazać, niech położenie r wagonu na rampie pod kątem θ powyżej poziomu będzie określone wzorem

${\ Displaystyle \ mathbf {r} = R (\ cos \ teta, \ sin \ teta),}$

gdzie R jest odległością wzdłuż rampy. Prędkość samochodu na rampie wynosi teraz

${\ Displaystyle \ mathbf {v} = V (\ cos \ teta, \ sin \ teta).}$

Ponieważ nie ma strat, moc użyta przez siłę F do przesunięcia ładunku po rampie jest równa mocy wyjściowej, która jest pionowym uniesieniem ciężaru W ładunku.

Moc wejściowa wciągająca samochód w górę rampy jest dana przez

${\ Displaystyle P _ {\ operatorname {w}} = FV, \!}$

a zasilanie jest

${\ Displaystyle P _ {\ operatorname {na zewnątrz}} = \ mathbf {W} \ cdot \ mathbf {v} = (0, W) \ cdot V (\ cos \ teta, \ sin \ teta) = WV \ sin \ teta .}$

Zrównaj moc wejściową z mocą wyjściową, aby uzyskać przewagę mechaniczną jako

${\ Displaystyle \ operatorname {MA} = {\ Frac {W} {F}} = {\ Frac {1} {\ sin \ theta}}.}$

Mechaniczną zaletę pochyłej płaszczyzny można również obliczyć ze stosunku długości pochylni L do jej wysokości H, ponieważ sinus kąta pochylni jest określony wzorem

${\ Displaystyle \ sin \ teta = {\ Frac {H} {L}},}$

W związku z tym,

${\ Displaystyle \ operatorname {MA} = {\ Frac {W} {F}} = {\ Frac {L} {H}}.}$

Układ układu napędu linowego dla pochylni Liverpool Minard.

Przykład: Jeżeli wysokość rampy wynosi H = 1 metr, a jej długość wynosi L = 5 metrów, wówczas przewaga mechaniczna wynosi

${\ Displaystyle \ operatorname {MA} = {\ Frac {W} {F}} = 5,}$

co oznacza, że ​​siła 20 funtów podniesie ładunek o masie 100 funtów.

Nachylona płaszczyzna Liverpool Minard ma wymiary 1804 na 37,50 metra, co zapewnia mechaniczną przewagę

${\ Displaystyle \ operatorname {MA} = {\ Frac {W} {F}} = 1804/37,50 = 48,1,}$

więc siła naciągu 100 funtów na kablu podniesie ładunek 4810 funtów. Nachylenie tego nachylenia wynosi 2%, co oznacza, że ​​kąt θ jest na tyle mały, że sin θ≈tan θ.

Zobacz też

• Nachylona płaszczyzna kanału
• Stopień (nachylenie)
• Pochylona linia kolejowa
• Funkcja rampy
• Schiefe Ebene
• Schody

Linki zewnętrzne

• Interaktywna symulacja pochyłej płaszczyzny fizyki