Praca (fizyka)

Aby zapoznać się z innymi zastosowaniami „Pracy” w fizyce, zobacz Praca (elektryczna) i Praca (termodynamika) .

Praca
Miotacz bejsbolowy wykonuje dodatnią pracę nad piłką, przykładając do niej siłę na odległość, na jaką się porusza, gdy jest w jego uścisku .
Wspólne symbole	W
jednostka SI	dżul (J)
Inne jednostki	Funt na stopę , Erg
W jednostkach podstawowych SI	1 kg ⋅ m 2 ⋅ s −2
Pochodne z innych wielkości	W = fa ⋅ s W = τ θ
Wymiar	M L 2 T −2

W fizyce praca to energia przenoszona do lub z obiektu poprzez przyłożenie siły wzdłuż przemieszczenia . W najprostszej postaci, dla stałej siły zgodnej z kierunkiem ruchu, praca jest równa iloczynowi siły siły i przebytej drogi. Mówi się, że siła wykonuje pracę dodatnią , jeśli po przyłożeniu ma składową w kierunku przemieszczenia punktu przyłożenia. Siła wykonuje pracę ujemną jeżeli ma składową przeciwną do kierunku przemieszczenia w punkcie przyłożenia siły.

Na przykład, gdy piłka jest trzymana nad ziemią, a następnie upuszczona, praca wykonana przez siłę grawitacji na spadającej piłce jest dodatnia i równa się ciężarowi piłki (siła) pomnożonemu przez odległość do ziemia (przemieszczenie). Jeśli piłka zostanie rzucona w górę, praca wykonana przez jej ciężar jest ujemna i równa się ciężarowi pomnożonemu przez przemieszczenie w górę.

Gdy siła F jest stała, a kąt między siłą a przemieszczeniem s wynosi θ , wówczas wykonaną pracę wyraża wzór:

$${\ Displaystyle W = Fs \ sałata {\ teta}}$$

Praca jest wielkością skalarną , więc ma tylko wielkość i nie ma kierunku. Praca przenosi energię z jednego miejsca do drugiego lub z jednej formy do drugiej. Jednostką pracy w układzie SI jest dżul (J), ta sama jednostka, co energia.

Historia

Starożytne greckie rozumienie fizyki ograniczało się do statyki prostych maszyn (równowaga sił) i nie obejmowało dynamiki ani pojęcia pracy. W okresie renesansu dynamikę sił mechanicznych , jak nazywano proste maszyny , zaczęto badać z punktu widzenia tego, jak daleko mogą podnieść ciężar, oprócz siły, jaką mogą zastosować, co ostatecznie doprowadziło do nowej koncepcji mechaniki. praca. Pełną dynamiczną teorię prostych maszyn opracował włoski naukowiec Galileo Galilei w 1600 roku w Le Meccaniche ( O mechanice ), w którym wykazał leżące u podstaw matematyczne podobieństwo maszyn jako wzmacniaczy siły. Jako pierwszy wyjaśnił, że proste maszyny nie wytwarzają energii, tylko ją przekształcają.

Etymologia

Według podręcznika fizyki Maxa Jammera z 1957 r ., termin praca został wprowadzony w 1826 r. przez francuskiego matematyka Gasparda-Gustave'a Coriolisa jako „ciężar podniesiony na wysokość”, co opiera się na wykorzystaniu wczesnych silników parowych do podnoszenia wiader z wodą zalanych kopalń rudy. Według Rene Dugasa, francuskiego inżyniera i historyka, to właśnie Salomonowi z Caux „zawdzięczamy termin praca w takim sensie, w jakim jest on obecnie używany w mechanice”.

Chociaż praca była formalnie używana dopiero w 1826 roku, podobne koncepcje istniały już wcześniej. W 1759 roku John Smeaton opisał wielkość, którą nazwał „mocą”, „oznaczającą wywieranie siły, grawitacji, impulsu lub ciśnienia w celu wywołania ruchu”. Smeaton kontynuuje, że tę wielkość można obliczyć, jeśli „podniesiony ciężar zostanie pomnożony przez wysokość, na jaką można go podnieść w danym czasie”, co czyni tę definicję niezwykle podobną do definicji Coriolisa.

Jednostki

Jednostką pracy w układzie SI jest dżul (J), nazwany na cześć dziewiętnastowiecznego angielskiego fizyka Jamesa Prescotta Joule'a , który definiuje się jako pracę wymaganą do wywarcia siły jednego niutona na przemieszczenie o jeden metr .

Wymiarowo równoważny niutonometr (N⋅m) jest czasami używany jako jednostka miary pracy, ale można ją pomylić z jednostką miary momentu obrotowego . Organ SI odradza stosowanie N⋅m , ponieważ może to prowadzić do nieporozumień co do tego, czy wielkość wyrażona w niutonometrach jest miarą momentu obrotowego, czy miarą pracy.

Jednostki pracy spoza układu SI obejmują niutonometr, erg , funt na stopę , funt na stopę , kilowatogodzinę , litr atmosfery i koni mechanicznych na godzinę . Ze względu na to, że praca ma ten sam wymiar fizyczny co ciepło , czasami jako jednostki miary używane są jednostki zwykle zarezerwowane dla ciepła lub zawartości energii, takie jak term , BTU i kalorie .

Praca i energia

Praca W wykonana przez stałą siłę o wartości F nad punktem, który przesuwa przemieszczenie s po linii prostej w kierunku działania siły, jest iloczynem

$${\ Displaystyle W = Fs.}$$

Na przykład, jeśli siła 10 niutonów ( F = 10 N ) działa wzdłuż punktu, który znajduje się w odległości 2 metrów ( s = 2 m ), to W = Fs = (10 N) (2 m) = 20 J . Jest to w przybliżeniu praca wykonana przy podnoszeniu przedmiotu o masie 1 kg z poziomu gruntu nad głowę osoby wbrew sile grawitacji.

Pracę podwaja się, podnosząc dwukrotnie ten sam ciężar na tę samą odległość lub podnosząc ten sam ciężar na dwukrotnie większą odległość.

Praca jest ściśle związana z energią . Zasada pracy i energii mówi, że wzrost energii kinetycznej ciała sztywnego jest spowodowany taką samą dodatnią pracą wykonaną na tym ciele przez wypadkową siłę działającą na to ciało. I odwrotnie, spadek energii kinetycznej jest spowodowany taką samą ilością ujemnej pracy wykonanej przez wypadkową siłę. Tak więc, jeśli praca netto jest dodatnia, to energia kinetyczna cząstki wzrasta o wielkość pracy. Jeśli wykonana praca netto jest ujemna, to energia kinetyczna cząstki zmniejsza się o ilość pracy.

Z drugiego prawa Newtona można wykazać, że praca nad ciałem swobodnym (bez pól), sztywnym (bez wewnętrznych stopni swobody) jest równa zmianie energii kinetycznej E _k odpowiadającej prędkości liniowej i prędkości kątowej tego ciała ,

$${\ Displaystyle W = \ Delta E _ {\ tekst {k}}.}$$

Praca sił generowanych przez funkcję potencjału jest znana jako energia potencjalna , a siły są uważane za zachowawcze . Dlatego praca nad obiektem, który jest jedynie przemieszczany w konserwatywnym polu sił , bez zmiany prędkości lub obrotu, jest równa minus zmiana energii potencjalnej E _p obiektu,

$${\ Displaystyle W = - \ Delta E _ {\ tekst {p}}.}$$

Wzory te pokazują, że praca jest energią związaną z działaniem siły, więc praca ma następnie fizyczne wymiary i jednostki energii. Omówione tutaj zasady praca/energia są identyczne z zasadami pracy/energii elektrycznej.

Siły ograniczające

Siły ograniczające określają przemieszczenie obiektu w układzie, ograniczając je w pewnym zakresie. Na przykład, w przypadku nachylenia plus grawitacja, obiekt przykleja się do zbocza, a po przymocowaniu do naprężonego sznurka nie może poruszać się w kierunku na zewnątrz, aby sznurek był „napięty”. Eliminuje wszystkie przemieszczenia w tym kierunku, czyli prędkość w kierunku ograniczenia jest ograniczona do 0, tak że siły ograniczające nie wykonują pracy nad układem.

W przypadku systemu mechanicznego siły ograniczające eliminują ruch w kierunkach charakteryzujących wiązanie. Zatem wirtualna praca wykonana przez siły ograniczające wynosi zero, co jest wynikiem, który jest prawdziwy tylko wtedy, gdy wykluczy się siły tarcia.

Stałe, beztarciowe siły ograniczające nie wykonują pracy nad układem, ponieważ kąt między ruchem a siłami ograniczającymi wynosi zawsze 90° . Przykładami ograniczeń bez pracy są: sztywne połączenia między cząstkami, ruch ślizgowy po powierzchni bez tarcia i kontakt toczny bez poślizgu.

Na przykład w systemie bloczków, takim jak maszyna Atwooda , siły wewnętrzne działające na linę i bloczek podtrzymujący nie działają na system. Dlatego pracę należy obliczyć tylko dla sił grawitacyjnych działających na ciała. Innym przykładem jest siła dośrodkowa wywierana do wewnątrz przez strunę na piłkę w ruchu jednostajnym po okręgu na boki , która ogranicza ruch piłki do ruchu kołowego, ograniczając jej ruch od środka koła. Ta siła wykonuje pracę zerową, ponieważ jest prostopadła do prędkości piłki.

Siła magnetyczna działająca na naładowaną cząstkę wynosi F = q v × B , gdzie q to ładunek, v to prędkość cząstki, a B to pole magnetyczne . Wynik iloczynu krzyżowego jest zawsze prostopadły do ​​obu pierwotnych wektorów, więc F ⊥ v . Iloczyn skalarny dwóch prostopadłych wektorów zawsze wynosi zero, więc praca W = F ⋅ v = 0 , a siła magnetyczna nie działa. Może zmieniać kierunek ruchu, ale nigdy nie zmieniać prędkości.

Obliczenia matematyczne

W przypadku poruszających się obiektów ilość pracy/czasu (mocy) jest całkowana wzdłuż trajektorii punktu przyłożenia siły. Tak więc w każdej chwili szybkość pracy wykonanej przez siłę (mierzona w dżulach na sekundę lub watach ) jest iloczynem skalarnym siły (wektor) i wektorem prędkości punktu przyłożenia. Ten skalarny iloczyn siły i prędkości jest znany jako moc chwilowa . Podobnie jak prędkości można całkować po czasie, aby uzyskać całkowitą odległość, za pomocą podstawowego twierdzenia rachunku różniczkowego , całkowita praca wzdłuż ścieżki jest podobnie całką po czasie mocy chwilowej przyłożonej wzdłuż trajektorii punktu przyłożenia.

Praca jest wynikiem działania siły na punkt biegnący po krzywej X z prędkością v w każdej chwili. Niewielka ilość pracy δW , która występuje w chwili dt, jest obliczana jako

$${\ Displaystyle \ delta W = \ mathbf {F} \ cdot d \ mathbf {s} = \ mathbf {F} \ cdot \ mathbf {v} dt}$$

gdzie F ⋅ v jest potęgą nad chwilą dt . Suma tych niewielkich ilości pracy nad trajektorią punktu daje pracę,

$${\ Displaystyle W = \ int _ {t_ {1}} ^ { t_{2}}\mathbf {F} \cdot \mathbf {v} \,dt=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\tfrac {d\ mathbf {s} }{dt}}\,dt=\int _{C}\mathbf {F} \cdot d\mathbf {s} ,}$$

gdzie C jest trajektorią od x ( t ₁ ) do x ( t ₂ ). Ta całka jest obliczana wzdłuż trajektorii cząstki i dlatego mówi się, że jest zależna od drogi .

Jeśli siła jest zawsze skierowana wzdłuż tej linii, a wartość siły wynosi F , to ta całka upraszcza się do

$${\ Displaystyle W = \ int _ {C} F \, ds}$$

gdzie s jest przemieszczeniem wzdłuż linii. Jeśli F jest stała, oprócz tego, że jest skierowana wzdłuż linii, to całka dalej się upraszcza

$${\ Displaystyle W = \ int _ {C} F \, ds = F \ int _ {C} ds = Fs}$$

gdzie s jest przemieszczeniem punktu wzdłuż linii.

Obliczenia te można uogólnić dla stałej siły, która nie jest skierowana wzdłuż linii, po której następuje cząstka. W tym przypadku iloczyn skalarny F ⋅ d s = F cos θ ds , gdzie θ jest kątem między wektorem siły a kierunkiem ruchu, tj.

$${\ Displaystyle W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {s} = Fs \ cos \ theta.}$$

Gdy składowa siły jest prostopadła do przemieszczenia obiektu (na przykład gdy ciało porusza się po torze kołowym pod działaniem siły centralnej ), żadna praca nie jest wykonywana, ponieważ cosinus 90° wynosi zero. Tak więc grawitacja nie może wykonać żadnej pracy na planecie o orbicie kołowej (jest to idealne rozwiązanie, ponieważ wszystkie orbity są lekko eliptyczne). Ponadto nie wykonuje się żadnej pracy na ciele poruszającym się po okręgu ze stałą prędkością, podczas gdy jest ono ograniczone siłą mechaniczną, na przykład porusza się ze stałą prędkością w idealnej wirówce bez tarcia.

Praca wykonana przez zmienną siłę

Obliczenie pracy jako „siła razy prosty odcinek ścieżki” miałoby zastosowanie tylko w najprostszych okolicznościach, jak wspomniano powyżej. Jeśli siła się zmienia lub jeśli ciało porusza się po zakrzywionej ścieżce, prawdopodobnie obracającej się i niekoniecznie sztywnej, wówczas tylko ścieżka punktu przyłożenia siły jest istotna dla wykonanej pracy i tylko składowa siły równoległa do prędkość punktu przyłożenia wykonuje pracę (praca dodatnia w tym samym kierunku i ujemna w kierunku przeciwnym do prędkości). Ten składnik siły można opisać wielkością skalarną zwaną skalarną składową styczną ( F cos( θ ) , gdzie θ jest kątem między siłą a prędkością). A następnie najbardziej ogólną definicję pracy można sformułować w następujący sposób:

Praca siły to całka krzywoliniowa jej skalarnej składowej stycznej wzdłuż ścieżki jej punktu przyłożenia.

Jeśli siła jest zmienna (np. ściskanie sprężyny), musimy użyć rachunku różniczkowego, aby znaleźć wykonaną pracę. Jeśli siła jest określona wzorem F ( x ) (funkcja x ), to praca wykonana przez siłę wzdłuż osi x od a do b wynosi:

$${\ Displaystyle W = \ int _ {a} ^ {b} \ mathbf {F (s)} \ cdot d \ mathbf {s}}$$

Moment obrotowy i obrót

Para sił wynika z równych i przeciwstawnych sił działających na dwa różne punkty bryły sztywnej. Suma (wypadkowa) tych sił może się znosić, ale ich oddziaływanie na ciało to para lub moment obrotowy T . Pracę momentu obrotowego oblicza się jako

$${\ Displaystyle \ delta W = \ mathbf {T} \ cdot {\ boldsymbol {\ omega}} \, dt,}$$

gdzie T ⋅ ω jest potęgą chwili dt . Suma tych niewielkich ilości pracy nad trajektorią sztywnego ciała daje pracę,

$${\ Displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {T} \ cdot {\ boldsymbol {\ omega}} \, dt.}$$

Ta całka jest obliczana wzdłuż trajektorii bryły sztywnej z prędkością kątową ω , która zmienia się w czasie, a zatem mówi się, że jest zależna od drogi .

Jeśli wektor prędkości kątowej zachowuje stały kierunek, to przyjmuje postać,

$${\ Displaystyle {\ boldsymbol {\ omega}} = {\ kropka {\ fi}} \ mathbf {S},}$$

gdzie $jest$ obrotu wokół stałego wektora jednostkowego S . W tym przypadku praca momentu obrotowego staje się,

$${\ Displaystyle W = \ int _ {t_ {1}} ^{t_{2}}\mathbf {T} \cdot {\boldsymbol {\omega}}\,dt=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot \ mathbf {S} {\frac {d\phi}}{dt}}dt=\int _{C}\mathbf {T} \cdot \mathbf {S} \,d\phi,}$$

gdzie C jest trajektorią od ${\ Displaystyle \ phi (t_ {1})}$ do ${\ Displaystyle \ phi (t_ {2})}$ . Ta całka $zależy$ od trajektorii obrotowej dlatego jest zależna

Jeśli moment obrotowy jest wyrównany z wektorem prędkości kątowej tak, że ${\ displaystyle \ tau}$

$${\ Displaystyle \ mathbf {T} = \ tau \ mathbf {S}}$$

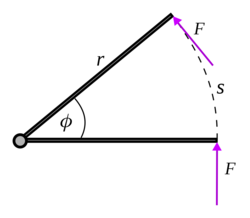
a zarówno moment obrotowy, jak i prędkość kątowa są stałe, wtedy praca przyjmuje postać,

$${\ Displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ tau {\ kropka {\ phi}} \, dt = \ tau (\ phi _ {2} - \ phi _ {1 }).}$$

Siła o stałej wielkości i prostopadła do ramienia dźwigni

$,$ biorąc pod uwagę moment obrotowy jako wynikający z siły o stałej wielkości F , przyłożonej prostopadle do ramienia dźwigni w odległości jak pokazano na rysunku. $ta będzie$ na odległość wzdłuż łuku kołowego wykonana

$${\ Displaystyle W = Fs = Fr \ phi.}$$

Wprowadź moment obrotowy τ = Fr , aby otrzymać

$${\ Displaystyle W = Fr \ phi = \ tau \ phi,}$$

jak przedstawiono powyżej.

Zauważ, że tylko składowa momentu obrotowego w kierunku wektora prędkości kątowej bierze udział w pracy.

Praca i energia potencjalna

Iloczyn skalarny siły F i prędkości v punktu jej przyłożenia określa moc wejściową do układu w danej chwili. Całkowanie tej mocy po trajektorii punktu przyłożenia, C = x ( t ) , określa pracę włożoną do układu przez siłę.

Zależność od ścieżki

Dlatego praca wykonana przez siłę F na obiekcie poruszającym się po krzywej C jest wyrażona całką krzywoliniową :

$${\ Displaystyle W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {x} = \ int _ {t_ {1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt,}$$

gdzie dx ( t ) definiuje trajektorię C , a v jest prędkością wzdłuż tej trajektorii. Ogólnie rzecz biorąc, ta całka wymaga, aby ścieżka, wzdłuż której zdefiniowana jest prędkość, więc mówi się, że ocena pracy jest zależna od ścieżki.

Pochodna czasowa całki po pracy daje moc chwilową,

$${\ Displaystyle {\ Frac {dW} {dt}} = P (t) = \ mathbf {F} \ cdot \ mathbf {v}.}$$

Niezależność ścieżki

Jeśli praca dla przyłożonej siły jest niezależna od drogi, to praca wykonana przez siłę, zgodnie z twierdzeniem o gradiencie , definiuje funkcję potencjału, która jest oceniana na początku i na końcu trajektorii punktu przyłożenia. Oznacza to x ( t2 ₎ , że istnieje potencjalna funkcja U ( x ) , _którą x ( t1 ) można obliczyć w dwóch punktach i aby uzyskać pracę nad dowolną trajektorią między tymi dwoma punktami. Tradycją jest definiowanie tej funkcji znakiem ujemnym, aby pozytywna praca była redukcją potencjału, tj

$${\ Displaystyle W = \ int _ {C} \ mathbf {F} \ cdot d \ mathbf {x} = \ int _ {\ mathbf {x} (t_ {1})} ^ {\ mathbf {x} (t_ {2})}\mathbf {F} \cdot d\mathbf {x} = U(\mathbf {x} (t_{1}))-U(\mathbf {x} (t_{2})).}$$

Funkcja U ( x ) nazywana jest energią potencjalną związaną z przyłożoną siłą. Mówi się, że siła wynikająca z takiej funkcji potencjału jest zachowawcza . Przykładami sił, które mają energię potencjalną, są siły grawitacji i siły sprężystości.

W tym przypadku gradient wydajności pracy

$${\ Displaystyle \ nabla W = - \ nabla U = - \ lewo ({\ Frac {\ częściowe U }{\częściowy x}},{\frac {\częściowy U}{\częściowy y}},{\frac {\częściowy U}{\częściowy z}}\right)=\mathbf {F},}$$

i mówi się, że siła F jest „wyprowadzalna z potencjału”.

Ponieważ potencjał U definiuje siłę F w każdym punkcie x w przestrzeni, zbiór sił nazywany jest polem siłowym . Moc przyłożona do ciała przez pole siłowe jest uzyskiwana z gradientu pracy lub potencjału w kierunku prędkości V ciała, to znaczy

$${\ Displaystyle P (t) = - \ nabla U \ cdot \ mathbf {v} = \ mathbf {F} \ cdot \ mathbf {v}.}$$

Pracuj grawitacyjnie

Grawitacja F = mg działa W = mgh wzdłuż dowolnej opadającej ścieżki

Przy braku innych sił grawitacja powoduje stałe przyspieszenie w dół każdego swobodnie poruszającego się obiektu. W pobliżu powierzchni Ziemi przyspieszenie grawitacyjne wynosi g = 9,8 m⋅s ⁻² , a siła grawitacji działająca na obiekt o masie m wynosi F _g = mg . Wygodnie jest wyobrazić sobie tę siłę grawitacji skoncentrowaną w środku masy obiektu.

Jeśli przedmiot o ciężarze mg zostanie przesunięty w górę lub w dół o pionową odległość y ₂ − y ₁ , praca W wykonana nad tym przedmiotem wynosi:

$${\ Displaystyle W = F_ {g} (y_ {2} -y_ {1}) = F_ {g} \ Delta y = mg\Delta y}$$

gdzie F _g to waga (funty w jednostkach imperialnych i niutony w jednostkach SI), a Δ y to zmiana wysokości y . Zauważ, że praca wykonana przez grawitację zależy tylko od pionowego ruchu obiektu. Obecność tarcia nie wpływa na pracę wykonaną na obiekcie przez jego ciężar.

Praca grawitacyjna w kosmosie

Siła grawitacji wywierana przez masę M na inną masę m jest dana wzorem

$$} {\ kapelusz {\ mathbf { r} }}=-{\frac {GMm}{r^{3}}}\mathbf {r} ,}$$

gdzie r jest wektorem położenia od M do m , a r̂ jest wektorem jednostkowym w kierunku r .

Niech masa m porusza się z prędkością v ; wtedy praca grawitacji nad tą masą, gdy porusza się ona z położenia r ( t ₁ ) do r ( t ₂ ) jest dana wzorem

$${\ Displaystyle W = - \ int _ {\ mathbf {r} (t_ {1})} ^ {\ mathbf {r} (t_ {2})} {\ Frac {GMm} {r ^ {3}}} \mathbf {r} \cdot d\mathbf {r} =-\int _{t_{1}}^{t_{2}}{\frac {GMm}{r^{3}}}\mathbf {r} \cdot \mathbf {v} \,dt.}$$

Zauważ, że położenie i prędkość masy m są dane wzorem

$${\ Displaystyle \ mathbf {r} = r \ mathbf {e} _ {r}, \ qquad \ mathbf {v } = {\frac {d\mathbf {r} }{dt}}={\dot {r}}\mathbf {e} _ {r}+r{\dot {\theta}}\mathbf {e} _ {T},}$$

gdzie er _i e t _że ${\ Displaystyle d \ mathbf {e} _ {r}/dt = {\ kropka {\ theta}} \ mathbf {e} _ {t}.} Użyj tego, aby uprościć wzór na pracę grawitacji do$ promieniowe i styczne wektory jednostkowe skierowane względem wektora od M do m , i wykorzystujemy fakt, ,

$${\ Displaystyle W = - \ int _ {t_ {1}} ^ {t_ {2}} {\ Frac {GM} {r ^ {3}}} (r \ mathbf {e} _ {r}) \ cdot \left({\dot {r}}\mathbf {e} _{r}+r{\dot {\theta}}\mathbf {e} _{t}\right)dt=-\int _{t_{ 1}}^{t_{2}}{\frac {GmM}{r^{3}}}r{\dot {r}}dt={\frac {GMm}{r(t_{2})}} -{\frac {GMm}{r(t_{1})}}.}$$

To obliczenie wykorzystuje fakt, że

$${\ Displaystyle {\ Frac {d} {dt}} r ^ {-1} = - r ^ {- 2} {\ kropka {r}} = - {\ frac {\ kropka {r}} {r ^ { 2}}}.}$$

Funkcja

$${\ Displaystyle U = - {\ Frac {GMm} {r}}}$$

jest funkcją potencjału grawitacyjnego, znaną również jako energia potencjalna grawitacji . Znak ujemny jest zgodny z konwencją, że praca jest uzyskiwana z utraty energii potencjalnej.

Pracuj przy źródle

Siły w sprężynach zmontowanych równolegle

Rozważmy sprężynę, która wywiera poziomą siłę F = (− kx , 0, 0) , która jest proporcjonalna do jej ugięcia w kierunku x , niezależnie od ruchu ciała. Praca tej sprężyny nad ciałem poruszającym się w przestrzeni po krzywej X ( t ) = ( x ( t ), y ( t ), z ( t )) , jest obliczana na podstawie jej prędkości v = ( v _x , v _tak , v _z ) , aby uzyskać

$${\ Displaystyle W = \ int _ {0} ^ {t} \ mathbf {F} \ cdot \ mathbf {v} dt = - \ int _ {0} ^ {t} kxv_ {x} dt = - {\ frac {1}{2}}kx^{2}.}$$

1/2 wygody xv x ² rozważmy, że kontakt ze sprężyną ma miejsce w chwili t = 0 , wtedy całka iloczynu odległości x i prędkości x, x _dt , po czasie t wynosi . Praca jest iloczynem odległości pomnożonej przez siłę sprężyny, która również zależy od odległości; stąd wynik x2 ^.

Praca przy gazie

Praca wykonana przez ciało gazowe na jego otoczeniu to: ${\ displaystyle W}$

$${\ Displaystyle W = \ int _ {a} ^ {b} P \, dV}$$

gdzie P to ciśnienie, V to objętość, a aib to objętość początkowa i końcowa.

Zasada pracy i energii

Zasada pracy i energii kinetycznej (znana również jako zasada pracy i energii ) mówi, że praca wykonana przez wszystkie siły działające na cząstkę (praca siły wypadkowej) jest równa zmianie energii kinetycznej cząstki. Oznacza to, że praca W wykonana przez wypadkową siłę na cząstce jest równa zmianie energii kinetycznej cząstki mi $\ displaystyle E _ {\ tekst {k}}}$ ,

$${\ Displaystyle W = \ Delta E _ {\ tekst {k}} = {\ Frac {1} {2}} mv_ {2} ^ {2}-{\frac {1}{2}}mv_{1}^{2}}$$

gdzie i są prędkościami cząstki przed i po $wykonaniu$ , a m $jest$

Wyprowadzenie zasady praca-energia zaczyna się od drugiego prawa dynamiki Newtona i wypadkowa siła działająca na cząstkę. Obliczenie iloczynu skalarnego siły przez prędkość cząstki ocenia chwilową moc dodaną do układu. (Ograniczenia określają kierunek ruchu cząstki, zapewniając, że nie ma składowej prędkości w kierunku siły ograniczającej. Oznacza to również, że siły ograniczające nie sumują się do mocy chwilowej.) Całka po czasie tego równania skalarnego daje pracę z mocy chwilowej, a energię kinetyczną ze skalarnego iloczynu przyspieszenia z prędkością. Fakt, że zasada praca-energia eliminuje siły ograniczające, leży u podstaw mechaniki Lagrange'a .

Ta sekcja skupia się na zasadzie praca-energia w odniesieniu do dynamiki cząstek. W bardziej ogólnych systemach praca może zmienić energię potencjalną urządzenia mechanicznego, energię cieplną w systemie termicznym lub energię elektryczną w urządzeniu elektrycznym. Praca przenosi energię z jednego miejsca do drugiego lub z jednej formy do drugiej.

Wyprowadzenie dla cząstki poruszającej się po linii prostej

W przypadku, gdy wypadkowa siła F jest stała zarówno pod względem wielkości, jak i kierunku oraz jest równoległa do prędkości cząstki, cząstka porusza się ze stałym przyspieszeniem a wzdłuż linii prostej. Zależność między siłą wypadkową a przyspieszeniem wyraża równanie F = ma ( drugie prawo Newtona ), a przemieszczenie cząstki s można wyrazić równaniem

$${\ Displaystyle s = {\ Frac {v_ {2} ^ {2} -v_ {1} ^ {2}} {2a}}}$$

co $_$ _ _ _

Praca siły netto jest obliczana jako iloczyn jej wielkości i przemieszczenia cząstki. Podstawiając powyższe równania otrzymujemy:

$${\ Displaystyle W = Fs = mas = ma {\ Frac { v_{2}^{2}-v_{1}^{2}}{2a}}={\frac {mv_{2}^{2}}{2}}-{\frac {mv_{1}^ {2}}{2}}=\Delta E_{\text{k}}}$$

Inne wyprowadzenie:

$${\ Displaystyle W = Fs = mas = m {\ frac {v_{2}^{2}-v_{1}^{2}}{2s}}s={\frac {1}{2}}mv_{2}^{2}-{\frac {1 }{2}}mv_{1}^{2}=\Delta E_{\text{k}}}$$

W ogólnym przypadku ruchu prostoliniowego, gdy siła wypadkowa F nie jest stała co do wartości, ale ma stały kierunek i jest równoległa do prędkości cząstki, praca musi być zintegrowana wzdłuż ścieżki cząstki:

$${\ Displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = \ int _ {t_ {1}} ^ {t_ {2} }F\,v\,dt=\int _{t_{1}}^{t_{2}}ma\,v\,dt=m\int _{t_{1}}^{t_{2}} v\,{\frac {dv}{dt}}\,dt=m\int _{v_{1}}^{v_{2}}v\,dv={\tfrac {1}{2}}m \left(v_{2}^{2}-v_{1}^{2}\right).}$$

Ogólne wyprowadzenie zasady praca-energia dla cząstki

Dla dowolnej siły wypadkowej działającej na cząstkę poruszającą się po dowolnej krzywoliniowej ścieżce można wykazać, że jej praca jest równa zmianie energii kinetycznej cząstki za pomocą prostego wyprowadzenia analogicznego do powyższego równania. Jest to znane jako zasada praca-energia :

$${\ Displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot \ mathbf {v} dt = m\int _{t_{1}}^{t_{2}}\mathbf {a} \cdot \mathbf {v} dt={\frac {m}{2}}\int _{t_{1}} ^{t_{2}}{\frac {dv^{2}}{dt}}\,dt={\frac {m}{2}}\int _{v_{1}^{2}}^{ v_{2}^{2}}dv^{2}={\frac {mv_{2}^{2}}{2}}-{\frac {mv_{1}^{2}}{2}} =\Delta E_{\text{k}}}$$

tożsamość ${\ textstyle \ mathbf {a} \ cdot \ mathbf {v} = {\ Frac {1} {2}} {\ frac {dv ^ {2}}} dt}}}$ wymaga pewnej algebry. Z tożsamości ${\ textstyle v ^ {2} = \ mathbf {v} \ cdot \ mathbf {v}}$ i definicji ${\ textstyle \ mathbf {a} = {\ frac {d\mathbf {v} }{dt}}}$ wynika

$${\ Displaystyle {\ Frac {dv ^ {2}}} {dt}} = {\ Frac {d (\ mathbf {v} \ cdot \ mathbf {v})} {dt}} = {\ Frac {d \ mathbf {v} }{dt}}\cdot \mathbf {v} +\mathbf {v} \cdot {\frac {d\mathbf {v} }{dt}}=2{\frac {d\mathbf {v} }{dt}}\cdot \mathbf {v} =2\mathbf {a} \cdot \mathbf {v} .}$$

Pozostała część powyższego wyprowadzenia to zwykły rachunek różniczkowy, taki sam jak w poprzednim przypadku prostoliniowym.

Wyprowadzenie dla cząstki w ruchu wymuszonym

W dynamice cząstek wzór zrównujący pracę układu ze zmianą jego energii kinetycznej otrzymuje się jako pierwszą całkę drugiej zasady dynamiki Newtona . Warto zauważyć, że wypadkową siłę używaną w prawach Newtona można podzielić na siły działające na cząstkę i siły narzucone przez ograniczenia ruchu cząstki. Co ciekawe, praca siły ograniczającej wynosi zero, dlatego w zasadzie praca-energia należy wziąć pod uwagę tylko pracę przyłożonych sił.

Aby to zobaczyć, rozważmy cząstkę P poruszającą się po trajektorii X ( t ) z działającą na nią siłą F. Odizoluj cząstkę od jej otoczenia, aby odsłonić siły ograniczające R , a następnie przybierze postać Prawo Newtona

$${\ Displaystyle \ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}},}$$

gdzie m jest masą cząstki.

Formuła wektorowa

Zauważ, że n kropek nad wektorem oznacza jego n-tą pochodną czasową . Iloczyn skalarny każdej strony prawa Newtona z wektorem prędkości daje

$${\ Displaystyle \ mathbf {F} \ cdot {\ kropka {\ mathbf {X}}} = m {\ ddot {\ mathbf {X}}} \ cdot {\ kropka {\mathbf {X}}},}$$

ponieważ siły ograniczające są prostopadłe do prędkości cząstek. Zintegruj to równanie wzdłuż jego trajektorii od punktu X ( t ₁ ) do punktu X ( t ₂ ) , aby otrzymać

$${\ Displaystyle \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ kropka {\ mathbf {X}}} dt = m \ int _ {t_ {1}} ^ {t_{2}}{\ddot {\mathbf {X}}}\cdot {\dot {\mathbf {X}}}dt.}$$

do _praca przyłożonej siły działającej na cząstkę wzdłuż trajektorii od czasu t2 _t1 czasu . Można to również zapisać jako

$${\ Displaystyle W = \ int _ {t_ {1}} ^ {t_ {2}} \ mathbf {F} \ cdot {\ kropka {\ mathbf {X}}} dt = \ int _ {\ mathbf {X} (t_{1})}^{\mathbf {X} (t_{2})}\mathbf {F} \cdot d\mathbf {X} .}$$

Całka ta jest obliczana wzdłuż trajektorii X ( t ) cząstki, a zatem jest zależna od drogi.

Prawą stronę pierwszej całki równań Newtona można uprościć za pomocą następującej tożsamości

$${\ Displaystyle {\ Frac {1} {2}} {\ Frac {d} {dt}} ({\ kropka {\ mathbf { X} }}\cdot {\dot {\mathbf {X}}})={\ddot {\mathbf {X}}}\cdot {\dot {\mathbf {X}}},}$$

(patrz reguła produktu dla wyprowadzenia). Teraz jest to całkowane jawnie, aby uzyskać zmianę energii kinetycznej,

$${\ Displaystyle \ Delta K = m \ int _ {t_ {1}} ^ {t_ {2}} {\ ddot {\ mathbf {X}}} \cdot {\dot {\mathbf {X}}}dt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {d}{dt} }({\dot {\mathbf {X}}}\cdot {\dot {\mathbf {X}}})dt={\frac {m}{2}}{\dot {\mathbf {X}}} \cdot {\dot {\mathbf {X}}}(t_{2})-{\frac {m}{2}}{\dot {\mathbf {X}}}\cdot {\dot {\mathbf { X} }}(t_{1})={\frac {1}{2}}m\Delta \mathbf {v} ^{2},}$$

gdzie energia kinetyczna cząstki jest określona przez wielkość skalarną,

$${\ Displaystyle K = {\ Frac {m} {2}} {\ kropka {\ mathbf {X}}} \ cdot {\ kropka {\ mathbf { X} }}={\frac {1}{2}}m{\mathbf {v} ^{2}}}$$

Składowe styczne i normalne

Przydatne jest rozłożenie wektorów prędkości i przyspieszenia na składowe styczne i normalne wzdłuż trajektorii X ( t ) , takie że

$${\ Displaystyle {\ kropka {\ mathbf {X}}} = v \ mathbf {T} \ quad {\ tekst {i}} \ quad {\ddot {\mathbf {X}}}={\dot {v}}\mathbf {T} +v^{2}\kappa \mathbf {N}}$$

Gdzie

$${\ Displaystyle v = | {\ kropka {\ mathbf {X}}} | = {\ sqrt {{\ kropka {\ mathbf {X}}} \ cdot {\ kropka {\ mathbf {X}}}}}. }$$

Wtedy iloczyn skalarny prędkości i przyspieszenia w drugim prawie Newtona przyjmuje postać

$${\ Displaystyle \ Delta K = m \ int _ {t_ {1}} ^ {t_ {2}} {\ kropka {v}} v \, dt = {\ frac {m} {2}} \ int _ { t_{1}}^{t_{2}}{\frac {d}{dt}}v^{2}\,dt={\frac {m}{2}}v^{2}(t_{2 })-{\frac {m}{2}}v^{2}(t_{1}),}$$

gdzie energia kinetyczna cząstki jest określona przez wielkość skalarną,

$${\ Displaystyle K = {\ Frac {m} {2}} v ^ {2} = {\ Frac {m} {2}}} {\ kropka {\ mathbf {X}}} \ cdot {\ kropka {\ mathbf {X} }}.}$$

Rezultatem jest zasada pracy i energii dla dynamiki cząstek,

$${\ Displaystyle W = \ Delta K.}$$

To wyprowadzenie można uogólnić na dowolne układy ciał sztywnych.

Poruszanie się po linii prostej (poślizg do zatrzymania)

Rozważmy przypadek pojazdu poruszającego się po prostej poziomej trajektorii pod działaniem siły napędowej i grawitacji, które sumują się do F . Siły ograniczające między pojazdem a drogą definiują R i mamy

$${\ Displaystyle \ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}}.}$$

Dla wygody niech trajektoria przebiega wzdłuż osi X, więc X = ( d , 0) i prędkość V = ( v , 0) , wtedy R ⋅ V = 0 i F ⋅ V = F _x v , gdzie F _x jest składową F wzdłuż osi X, więc

$${\ Displaystyle F_ {x} v = m {\ kropka {v}} v.}$$

Integracja obu stron daje plony

$${\ Displaystyle \ int _ {t_ {1}} ^ {t_ {2}} F_ {x} vdt = {\ Frac {m} {2}} v ^ {2} (t_ {2}) - {\ frac {m}{2}}v^{2}(t_{1}).}$$

Jeśli F _x jest stała wzdłuż trajektorii, to całka prędkości jest odległością, więc

$${\ Displaystyle F_ {x} (d (t_ {2}) -d (t_ {1})} = {\ Frac {m} {2}} v ^ {2} (t_ {2}) - {\ frac {m}{2}}v^{2}(t_{1}).}$$

Jako przykład rozważmy samochód wpadający w poślizg do zatrzymania, gdzie k to współczynnik tarcia, a W to masa samochodu. Wówczas siła wzdłuż trajektorii wynosi F _x = − kW . Prędkość v samochodu można wyznaczyć z długości poślizgu s, korzystając z zasady pracy i energii,

$${\ Displaystyle kWs = {\ Frac {W} {2g}} v ^ {2}, \ quad {\ tekst {lub}} \ quad v = {\ sqrt {2ksg}}.}$$

Zauważ, że ten wzór wykorzystuje fakt, że masa pojazdu wynosi m = W / g .

Lotus typ 119B grawitacyjny wyścigowiec na obchodach 60. rocznicy Lotus

Mistrzostwa w wyścigach grawitacyjnych w Campos Novos, Santa Catarina, Brazylia, 8 września 2010 r

Jazda po pochyłej powierzchni (wyścigi grawitacyjne)

Rozważmy przypadek pojazdu, który rusza z miejsca i jedzie po pochyłej powierzchni (takiej jak górska droga), zasada pracy i energii pomaga obliczyć minimalną odległość, jaką pokonuje pojazd, aby osiągnąć prędkość V , powiedzmy 60 mil na godzinę ( 88 fps ). Opór toczenia i opór powietrza spowalniają pojazd, więc rzeczywista odległość będzie większa niż w przypadku pominięcia tych sił.

Niech trajektoria pojazdu podążającego drogą będzie równa X ( t ) , która jest krzywą w przestrzeni trójwymiarowej. Siła działająca na pojazd, która popycha go w dół drogi, to stała siła grawitacji F = (0, 0, W ) , natomiast siła działająca na pojazd to siła ograniczająca R . Drugie prawo Newtona daje,

$${\ Displaystyle \ mathbf {F} + \ mathbf {R} = m {\ ddot {\ mathbf {X}}}.}$$

Iloczyn skalarny tego równania z prędkością V = ( v _x , v _y , v _z ) daje

$${\ Displaystyle Wv_ {z} = m {\ kropka {V}} V,}$$

gdzie V jest wielkością V . Siły wiążące między pojazdem a drogą znoszą się z tego równania, ponieważ R ⋅ V = 0 , co oznacza, że ​​nie wykonują pracy. Zintegruj obie strony, aby otrzymać

$${\ Displaystyle \ int _ {t_ {1}} ^ {t_ {2}} Wv_ {z} dt = {\ Frac {m} {2}} V ^ {2} (t_ {2}) - {\ frac {m}{2}}V^{2}(t_{1}).}$$

Siła ciężkości W jest stała wzdłuż trajektorii, a całka prędkości pionowej jest odległością pionową, dlatego

$${\ Displaystyle W \ Delta z = {\ Frac {m} {2}} V ^ {2}.}$$

Przypomnijmy, że V( t ₁ )=0. Należy zauważyć, że wynik ten nie zależy od kształtu drogi, po której porusza się pojazd.

Aby określić odległość wzdłuż drogi, załóżmy, że spadek wynosi 6%, co oznacza stromą drogę. Oznacza to, że wysokość spada o 6 stóp na każde przebyte 100 stóp — dla tak małych kątów funkcje sin i tan są w przybliżeniu równe. Dlatego odległość s w stopach w dół o nachylenie 6%, aby osiągnąć prędkość V, wynosi co najmniej

$${\ Displaystyle s = {\ Frac {\ Delta Z} {0,06}} = 8,3 {\ Frac {V ^ {2}} {g}}, \ quad {\ tekst {lub}} \ quad s = 8,3 {\ frac {88^{2}}{32.2}}\około 2000\mathrm {ft} .}$$

Formuła ta wykorzystuje fakt, że masa pojazdu wynosi W = mg .

Praca sił działających na bryłę sztywną

Pracę sił działających w różnych punktach na pojedynczy sztywny korpus można obliczyć z pracy wypadkowej siły i momentu obrotowego . Aby to zobaczyć, _niech siły F ₁ , F ₂ , ..., Fn działają na punkty X ₁ , X ₂ , ..., X _n bryły sztywnej.

Trajektorie X _i , i = 1, ..., n są określone przez ruch bryły sztywnej. Ruch ten jest określony przez zbiór obrotów [ A ( t )] i trajektorię d ( t ) punktu odniesienia w ciele. Niech współrzędne x _i i = 1, ..., n definiują te punkty w układzie odniesienia poruszającego się ciała sztywnego M , tak aby trajektorie wytyczone w układzie nieruchomym F były dane wzorem

$${\ Displaystyle \ mathbf {X} _ {i} (t) = [A (t)] \ mathbf {x} _ {i} + \ mathbf {d} (t) \ quad i = 1, \ ldots, n .}$$

Prędkość punktów X _i wzdłuż ich trajektorii wynosi

$${\ Displaystyle \ mathbf {V} _ {i} = {\ boldsymbol {\ omega}} \ razy (\ mathbf {X} _ {i} -\ mathbf {d} )+ {\kropka {\mathbf {d}}},}$$

gdzie ω jest wektorem prędkości kątowej uzyskanym z skośnej symetrycznej macierzy

$${\ Displaystyle [\ Omega] = {\ kropka {A}} A ^ {\ mathsf {T}},}$$

znany jako macierz prędkości kątowych.

Niewielką pracę sił nad małymi przemieszczeniami δ r _i można określić przybliżając przemieszczenie przez δ r = v δt więc

$${\ Displaystyle \ delta W = \ mathbf {F} _ {1} \ cdot \ mathbf {V } _{1}\delta t+\mathbf {F} _{2}\cdot \mathbf {V} _{2}\delta t+\ldots +\mathbf {F} _{n}\cdot \mathbf {V} _{n}\delta t}$$

Lub

$${\ Displaystyle \ delta W = \ suma _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ cdot ({\ boldsymbol {\ omega}} \ razy (\ mathbf {X} _ {i } -\mathbf {d} )+{\kropka {\mathbf {d}}})\delta t.}$$

Tę formułę można przepisać, aby uzyskać

$${\ Displaystyle \ delta W = \ lewo (\ suma _ {i = 1} ^ {n} \ mathbf {F} _ {i} \ prawej) \ cdot {\ kropka {\ mathbf {d}}} \ delta t + \left(\sum _{i=1}^{n}\left(\mathbf {X} _{i}-\mathbf {d} \right)\times \mathbf {F} _{i}\right) \cdot {\boldsymbol {\omega}}\delta t=\left(\mathbf {F} \cdot {\dot {\mathbf {d}}}+\mathbf {T} \cdot {\boldsymbol {\omega} }\prawo)\delta t,}$$

gdzie F i T są wypadkową siłą i momentem obrotowym przyłożonym do punktu odniesienia d ruchomej ramy M w bryle sztywnej.

Bibliografia

•   Serway, Raymond A.; Jewett, John W. (2004). Fizyka dla naukowców i inżynierów (wyd. 6). Brooks/Cole. ISBN 0-534-40842-7 .
•   Tipler, Paweł (1991). Fizyka dla naukowców i inżynierów: Mechanika (wyd. 3, wyd. Wersja rozszerzona). WH Freemana. ISBN 0-87901-432-6 .

Linki zewnętrzne

• Zasada pracy i energii