Moment bezwładności
W naukach planetarnych moment bezwładności lub znormalizowany biegunowy moment bezwładności jest wielkością bezwymiarową , która charakteryzuje radialny rozkład masy wewnątrz planety lub satelity . Ponieważ moment bezwładności musi mieć wymiary masy razy długość do kwadratu, współczynnik momentu bezwładności jest współczynnikiem, który je mnoży.
Definicja
Dla ciała planetarnego z głównymi momentami bezwładności moment bezwładności definiuje się jako ZA
- ,
gdzie C to biegunowy moment bezwładności ciała, M to masa ciała, a R to średni promień ciała. Dla kuli o jednolitej gęstości , . Dla zróżnicowanej planety lub satelity, gdzie następuje wzrost gęstości wraz z głębokością, . Ilość jest użytecznym wskaźnikiem obecności i zasięgu jądra planetarnego , ponieważ większe odstępstwo od wartości jednorodnej gęstości wynoszącej 0,4 przenosi większy stopień koncentracji gęstych materiałów w kierunku centrum.
Wartości Układu Słonecznego
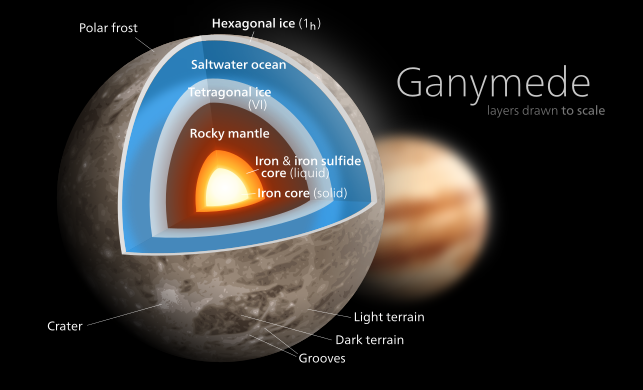
Słońce ma zdecydowanie najniższy moment bezwładności wśród ciał Układu Słonecznego ; ma zdecydowanie najwyższą gęstość centralną ( 162 g/cm 3 , w porównaniu do ~13 dla Ziemi ) i stosunkowo niską średnią gęstość (1,41 g/cm 3 w porównaniu do 5,5 dla Ziemi). Saturn ma najniższą wartość wśród gazowych olbrzymów , po części dlatego, że ma najniższą gęstość objętościową ( 0,687 g/cm 3 ). Ganimedes ma najniższy współczynnik bezwładności wśród ciał stałych w Układzie Słonecznym ze względu na w pełni zróżnicowane wnętrze, będące wynikiem częściowego ogrzewania pływowego w wyniku rezonansu Laplace'a , a także znacznego składnika lodu wodnego o niskiej gęstości . Callisto jest podobna pod względem wielkości i składu do Ganimedesa, ale nie jest częścią rezonansu orbitalnego i jest mniej zróżnicowana. Uważa się , że Księżyc ma małe jądro, ale poza tym jego wnętrze jest względnie jednorodne.
| Ciało | Wartość | Źródło | Notatki |
|---|---|---|---|
| Słońce | 0,070 | Niezmierzony | |
| Rtęć | 0,346 ± 0,014 | ||
| Wenus | 0,337 ± 0,024 | ||
| Ziemia | 0,3307 | ||
| Księżyc | 0,3929 ± 0,0009 | ||
| Mars | 0,3644 ± 0,0005 | ||
| Ceres | 0,36 ± 0,15 | Nie mierzono (zakres odzwierciedla różne założenia dotyczące pierwotnej prędkości wirowania) | |
| Jowisz | 0,2756 ± 0,0006 | Nie zmierzono (obliczenia modelu dwuwarstwowego ograniczone danymi grawitacyjnymi Juno) | |
| ja | 0,37824 ± 0,00022 | Nie mierzono (relacja Darwina-Radaua) | |
| Europa | 0,346 ± 0,005 | Nie mierzono (relacja Darwina-Radaua) | |
| Ganimedes | 0,3115 ± 0,0028 | Nie mierzono (relacja Darwina-Radaua) | |
| Kalisto | 0,3549 ± 0,0042 | Nie mierzono (relacja Darwina-Radaua) | |
| Saturn | 0,22 | Nie mierzono (relacja Darwina-Radaua) | |
| Enceladus | 0,3305 ± 0,0025 | Nie mierzono (relacja Darwina-Radaua) | |
| Rea | 0,3911 ± 0,0045 | Nie mierzono (relacja Darwina-Radaua) | |
| tytan | 0,341 | Nie mierzono (relacja Darwina-Radaua) | |
| Uran | 0,23 | Nie zmierzono (przybliżone rozwiązanie równania Clairauta) | |
| Neptun | 0,23 | Nie zmierzono (przybliżone rozwiązanie równania Clairauta) |
Pomiar
Biegunowy moment bezwładności jest tradycyjnie określany przez połączenie pomiarów wielkości spinowych ( szybkość precesji spinu i/lub nachylenie ) z wielkościami grawitacyjnymi (współczynnikami sferycznej harmonicznej reprezentacji pola grawitacyjnego). Zebranie tych danych geodezyjnych zwykle wymaga orbitującego statku kosmicznego .
Przybliżenie
W przypadku ciał w równowadze hydrostatycznej relacja Darwina -Radaua może zapewnić oszacowanie momentu bezwładności na podstawie wielkości kształtu, spinu i grawitacji.
Rola w modelach wnętrz
Czynnik momentu bezwładności stanowi ważne ograniczenie dla modeli reprezentujących strukturę wewnętrzną planety lub satelity. Akceptowalne modele profilu gęstości muszą co najmniej odpowiadać objętościowej gęstości masy i momentowi bezwładności ciała.
Galeria modeli konstrukcji wewnętrznych
Słońce ( C /MR 2 = 0,070)
Saturn ( C/MR 2 = 0,22)
Ganimedes ( C/MR 2 = 0,3115)
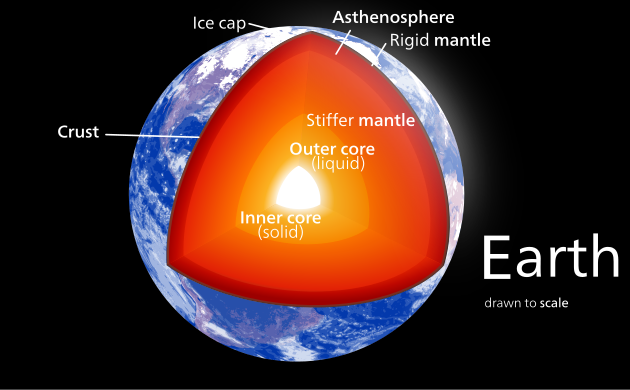
Ziemia ( C/MR 2 = 0,3307)
Kalisto ( C/MR 2 = 0,3549)
Księżyc ( C /MR 2 = 0,3929)