Dźwignia

Ten artykuł dotyczy prostej maszyny. W przypadku innych zastosowań zobacz Dźwignia (ujednoznacznienie) .

Dźwignie
mogą być używane do wywierania dużej siły na niewielką odległość na jednym końcu, wywierając tylko niewielką siłę (wysiłek) na większą odległość na drugim.
Klasyfikacja	Prosta maszyna
składniki	punkt podparcia lub obrót, obciążenie i wysiłek
Przykłady	huśtawka, otwieracz do butelek itp.

Dźwignia to prosta maszyna składająca się z belki lub sztywnego pręta obracanego na stałym zawiasie lub punkcie podparcia . Dźwignia jest sztywnym ciałem, które może obracać się wokół punktu na sobie. Na podstawie umiejscowienia punktu podparcia, obciążenia i siły dźwignia dzieli się na trzy typy . Dźwignia finansowa to także mechaniczna przewaga uzyskana w systemie. Jest to jedna z sześciu prostych maszyn zidentyfikowanych przez renesansowych naukowców. Dźwignia wzmacnia siłę wejściową, aby zapewnić większą siłę wyjściową, o której mówi się, że zapewnia dźwignia . Stosunek siły wyjściowej do siły wejściowej jest mechaniczną zaletą dźwigni. Jako taka, dźwignia jest mechanicznym urządzeniem zapewniającym przewagę , wymieniającym siłę na ruch.

Etymologia

Słowo „dźwignia” pojawiło się w języku angielskim około 1300 roku ze starofrancuskiego , w którym słowo to brzmiało „levier” . To wyrosło z rdzenia czasownika dźwignia , oznaczającego „podnieść”. Czasownik z kolei pochodzi od łacińskiego levare , od przymiotnika levis , oznaczającego „lekki” (jak w „nieciężkim”). Pierwotnym pochodzeniem tego słowa jest praindoeuropejski rdzeń legwh- , co oznacza między innymi „lekki”, „łatwy” lub „zwinny”. Rdzeń PIE dał również początek angielskiemu słowu „light”.

Historia

Najwcześniejsze dowody na istnienie mechanizmu dźwigniowego pochodzą ze starożytnego Bliskiego Wschodu około 5000 lat pne, kiedy to po raz pierwszy użyto go w prostej wadze równoważnej . W starożytnym Egipcie około 4400 rpne pedał nożny był używany do najwcześniejszego poziomego krosna ramowego . W Mezopotamii (współczesny Irak) około 3000 pne wynaleziono shadouf , urządzenie podobne do dźwigu, które wykorzystuje mechanizm dźwigniowy. W technologii starożytnego Egiptu robotnicy używali dźwigni do przesuwania i podnoszenia obelisków ważących ponad 100 ton. Widać to po zagłębieniach w dużych blokach i występach manipulacyjnych, które nie mogły służyć do innych celów niż dźwignie.

Najwcześniejsze zachowane pisma dotyczące dźwigni pochodzą z III wieku pne i zostały dostarczone przez greckiego matematyka Archimedesa , który słynnie stwierdził: „Dajcie mi wystarczająco długą dźwignię i punkt podparcia, na którym ją położę, a poruszę świat”.

Siła i dźwignie

Dźwignia w równowadze

Dźwignia to belka połączona z podłożem za pomocą zawiasu lub sworznia, zwanego punktem podparcia. Idealna dźwignia nie rozprasza ani nie magazynuje energii, co oznacza, że ​​nie występuje tarcie w zawiasie ani zginanie belki. W tym przypadku moc wprowadzona do dźwigni jest równa mocy wyjściowej, a stosunek mocy wyjściowej do siły wejściowej jest określony stosunkiem odległości od punktu podparcia do punktów przyłożenia tych sił. Jest to znane jako prawo dźwigni .

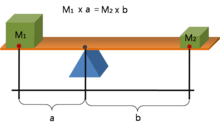
Mechaniczną zaletę dźwigni można określić, biorąc pod uwagę równowagę momentów lub momentu obrotowego T wokół punktu podparcia. Jeśli przebyta droga jest większa, siła wyjściowa jest mniejsza.

$${\ Displaystyle {\ rozpocząć {wyrównane} T_ {1} i = F_ {1} a, \ quad \\ T_ {2} i = F_ {2} b \ !\end{wyrównane}}}$$

gdzie F ₁ jest siłą wejściową działającą na dźwignię, a F ₂ jest siłą wyjściową. Odległości aib to prostopadłe odległości między siłami a punktem podparcia.

Ponieważ momenty momentu obrotowego muszą być zrównoważone, ${\ Displaystyle T_ {1} = T_ {2} \!}$ . Tak więc ${\ Displaystyle F_ {1} a = F_ {2} b \!$ }

Mechaniczną zaletą dźwigni jest stosunek siły wyjściowej do siły wejściowej.

$${\ Displaystyle MA = {\ Frac {F_ {2}} {F_ {1}}} = {\ Frac {a} {b}}. \!}$$

Ta zależność pokazuje, że mechaniczną przewagę można obliczyć ze stosunku odległości od punktu podparcia do miejsca, w którym siły wejściowe i wyjściowe są przykładane do dźwigni, zakładając brak strat spowodowanych tarciem, elastycznością lub zużyciem. Pozostaje to prawdą, mimo że odległość „pozioma” (prostopadła do przyciągania grawitacyjnego) zarówno a , jak i b zmienia się (zmniejsza), gdy dźwignia zmienia położenie z dala od poziomu.

Klasy dźwigni

Trzy klasy dźwigni

Trzy klasyfikacje dźwigni z przykładami ludzkiego ciała

Dźwignie są klasyfikowane według względnych pozycji punktu podparcia, wysiłku i oporu (lub obciążenia). Powszechnie nazywa się siłę wejściową wysiłkiem , a siłę wyjściową obciążeniem lub oporem. Pozwala to na identyfikację trzech klas dźwigni na podstawie względnego położenia punktu podparcia, oporu i wysiłku:

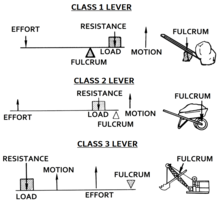
• Klasa I – Fulcrum między wysiłkiem a oporem: Wysiłek przykładany jest po jednej stronie punktu podparcia, a opór (lub obciążenie) po drugiej stronie, np. huśtawka , łom lub nożyczki , waga balansowa , młotek pazurowy . Przewaga mechaniczna może być większa, mniejsza lub równa 1.
• Klasa II – Opór ( lub obciążenie) między wysiłkiem a punktem podparcia: Wysiłek jest przykładany po jednej stronie oporu, a punkt podparcia znajduje się po drugiej stronie, np. w taczce, dziadku do orzechów , otwieraczu do butelek lub pedale hamulca samochód. Ramię obciążenia jest mniejsze niż ramię siły, a przewaga mechaniczna jest zawsze większa niż 1. Jest również nazywana dźwignią mnożnika siły.
• Klasa III – Wysiłek między punktem podparcia a oporem: Opór (lub obciążenie) znajduje się po jednej stronie wysiłku, a punkt podparcia po drugiej stronie, na przykład pęseta , młotek , szczypce , wędka lub żuchwa ludzkiej czaszki. Ramię wysiłkowe jest mniejsze niż ramię ładujące. Przewaga mechaniczna jest zawsze mniejsza niż 1. Jest również nazywana dźwignią mnożnika prędkości.

Przypadki te są opisane przez mnemoniczny fre 123 , gdzie punkt podparcia znajduje się między r i e dla dźwigni 1. klasy, opór r jest między f i e dla dźwigni 2. klasy, a wysiłek e jest między f i r dla dźwigni 3. dźwignia klasy.

Dźwignia złożona

Główny artykuł: dźwignia złożona

Dźwignia złożona składa się z kilku dźwigni działających szeregowo: opór jednej dźwigni w układzie dźwigni działa jak wysiłek dla następnej, a zatem przyłożona siła jest przenoszona z jednej dźwigni na drugą. Przykłady dźwigni złożonych obejmują łuski, obcinacze do paznokci i klawisze fortepianu.

Młoteczek , kowadełko i strzemiączko to małe kości w uchu środkowym , połączone jako dźwignie złożone, które przenoszą fale dźwiękowe z błony bębenkowej do okienka owalnego ślimaka .

Prawo dźwigni

Zobacz także: Przewaga mechaniczna § Dźwignia

Dźwignia to ruchomy pręt, który obraca się na punkcie podparcia przymocowanym do stałego punktu. Dźwignia działa poprzez przykładanie sił w różnych odległościach od punktu podparcia lub osi obrotu.

Gdy dźwignia obraca się wokół punktu podparcia, punkty znajdujące się dalej od tego punktu obrotu poruszają się szybciej niż punkty znajdujące się bliżej punktu obrotu. Dlatego siła przyłożona do punktu znajdującego się dalej od osi musi być mniejsza niż siła znajdująca się w punkcie bliżej, ponieważ moc jest iloczynem siły i prędkości.

Jeżeli a i b są odległościami od punktu podparcia do punktów A i B , a siła F _A przyłożona do A jest wartością wejściową, a siła F _B przyłożona do B jest wartością wyjściową, stosunek prędkości punktów A i B jest określony wzorem a/b , więc mamy stosunek siły wyjściowej do siły wejściowej, czyli przewagę mechaniczną, wyraża się wzorem:

$${\ Displaystyle MA = {\ Frac {F_ {B}} {F_ {A}}} = {\ Frac {a} {b}}.}$$

To jest prawo dźwigni , które zostało udowodnione przez Archimedesa za pomocą rozumowania geometrycznego. Pokazuje, że jeśli odległość a od punktu podparcia do miejsca przyłożenia siły wejściowej (punkt A ) jest większa niż odległość b od punktu podparcia do miejsca przyłożenia siły wyjściowej (punkt B ), to dźwignia wzmacnia siłę wejściową. Z drugiej strony, jeśli odległość a od punktu podparcia do siły wejściowej jest mniejsza niż odległość b od punktu podparcia do siły wyjściowej, wówczas dźwignia zmniejsza siłę wejściową.

Wykorzystanie prędkości w analizie statycznej dźwigni jest zastosowaniem zasady pracy wirtualnej .

Praca wirtualna i prawo dźwigni

Dźwignia jest modelowana jako sztywny pręt połączony z ramą uziemiającą za pomocą przegubu zwanego punktem podparcia. Dźwignia jest obsługiwana przez przyłożenie siły wejściowej F _A w punkcie A znajdującym się na pręcie przez wektor współrzędnych r _A. Dźwignia wywiera wówczas siłę wyjściową F _B w punkcie B położonym przez r _B . Obrót dźwigni wokół punktu podparcia P jest określony przez kąt obrotu θ w radianach.

Dźwignia Archimedesa, Grawerunek z Mechanics Magazine , opublikowany w Londynie w 1824 r

Niech wektorem współrzędnych punktu P , który definiuje punkt podparcia, będzie r _P i wprowadź długości

$${\ Displaystyle a = | \ mathbf {r} _ {A} - \ mathbf {r} _ {P} | \ quad b = | \ mathbf {r} _ {B} - \ mathbf {r} _ { P}|,}$$

które są odpowiednio odległościami od punktu podparcia do punktu wejściowego A i punktu wyjściowego B .

Teraz wprowadź wektory jednostkowe e _A i e _B od punktu podparcia do punktu A i B , więc

$${\ Displaystyle \ mathbf {r} _ {A} - \ mathbf {r} _ {P} = a \ mathbf {e} _ {A}, \ quad \ mathbf {r} _ {B} - \ mathbf {r } _{P}=b\mathbf {e} _{B}.}$$

Prędkość punktów A i B otrzymujemy jako

$${\ Displaystyle \ mathbf {v} _ {A} = {\ kropka {\ teta}} a \ mathbf {e} _ {$$

gdzie e _A ^⊥ i e _B ^⊥ są wektorami jednostkowymi prostopadłymi odpowiednio do e _A i e _B .

Kąt θ jest uogólnioną współrzędną , która określa konfigurację dźwigni, a uogólniona siła związana z tą współrzędną jest wyrażona wzorem

$${\ Displaystyle F _ {\ theta} = \ mathbf {F} _ {A} \ cdot {\ Frac {\ częściowe \ mathbf {v} _ {A}} {\ częściowe {\ kropka {\ teta}}}} - \mathbf {F} _{B}\cdot {\frac {\częściowo \mathbf {v} _{B}}{\częściowo {\dot {\theta}}}}=a(\mathbf {F} _{ A}\cdot \mathbf {e} _{A}^{\sprawa})-b(\mathbf {F} _{B}\cdot \mathbf {e} _{B}^{\sprawa})=aF_ {A}-bF_{B},}$$

gdzie F _A i F _B są składowymi sił prostopadłych do odcinków promieniowych PA i PB . Zasada pracy wirtualnej mówi, że w stanie równowagi siła uogólniona wynosi zero, to znaczy

$${\ Displaystyle F _ {\ teta} = aF_ {A} -bF_ {B} = 0. \, \!}$$

Prosta dźwignia, punkt podparcia i słupki pionowe

Zatem stosunek siły wyjściowej F _B do siły wejściowej F _A otrzymuje się jako

$$\ Displaystyle MA = {\ Frac {F_ {B}} {F_ {A}}} = {\ Frac {a} {b}},}$$

co jest mechaniczną zaletą dźwigni.

To równanie pokazuje, że jeśli odległość a od punktu podparcia do punktu A , w którym przyłożona jest siła wejściowa, jest większa niż odległość b od punktu podparcia do punktu B , w którym przyłożona jest siła wyjściowa, wówczas dźwignia wzmacnia siłę wejściową. Jeśli jest odwrotnie, że odległość od punktu podparcia do punktu wejściowego A jest mniejsza niż od punktu podparcia do punktu wyjściowego B , wówczas dźwignia zmniejsza wielkość siły wejściowej.

Zobacz też

• Mechanika stosowana – Praktyczne zastosowanie mechaniki
• Sprzęg dźwigni balansu
• Połączenie (mechaniczne) - Montaż systemów połączonych w celu zarządzania siłami i ruchem
• Mechanizm (inżynieria) - Urządzenie służące do przenoszenia sił za pomocą środków nieelektrycznych
• O równowadze płaszczyzn - traktat mechaniczny Archimedesa
• Prosta maszyna – urządzenie mechaniczne, które zmienia kierunek lub wielkość siły

Linki zewnętrzne

• Dźwignia w encyklopedii nauki i inżynierii Diracdelta
• A Simple Lever autorstwa Stephena Wolframa , Wolfram Demonstrations Project .
• Dźwignie: proste maszyny na EnchantedLearning.com