Suma Riemanna

Cztery metody aproksymacji pola pod krzywymi. Metody prawe i lewe dokonują aproksymacji przy użyciu odpowiednio prawego i lewego punktu końcowego każdego podprzedziału. Metody górna i dolna dokonują aproksymacji przy użyciu odpowiednio największej i najmniejszej wartości punktu końcowego każdego podprzedziału. Wartości sum zbiegają się, gdy podprzedziały zmniejszają się o połowę od lewego górnego rogu do prawego dolnego rogu.

W matematyce suma Riemanna jest pewnym rodzajem przybliżenia całki przez sumę skończoną. Jej nazwa pochodzi od dziewiętnastowiecznego niemieckiego matematyka Bernharda Riemanna . Jednym z bardzo powszechnych zastosowań jest aproksymacja obszaru funkcji lub linii na wykresie, ale także długości krzywych i innych aproksymacji.

Suma jest obliczana przez podzielenie obszaru na kształty ( prostokąty , trapezy , parabole lub sześciany ), które razem tworzą obszar podobny do mierzonego obszaru, następnie obliczenie powierzchni każdego z tych kształtów i na koniec dodanie wszystkich tych małe obszary razem. Podejście to można zastosować do znalezienia przybliżenia liczbowego dla całki oznaczonej , nawet jeśli podstawowe twierdzenie rachunku różniczkowego nie ułatwia znalezienia rozwiązania w postaci zamkniętej .

Ponieważ obszar o małych kształtach zwykle nie ma dokładnie takiego samego kształtu jak mierzony obszar, suma Riemanna będzie się różnić od mierzonego obszaru. Ten błąd można zmniejszyć, dzieląc obszar dokładniej, używając coraz mniejszych kształtów. Gdy kształty stają się coraz mniejsze, suma zbliża się do całki Riemanna .

Definicja

Niech ${\ Displaystyle f: [a, b] \ do \ mathbb {R}}$ będzie funkcją zdefiniowaną na przedziale zamkniętym ${\ Displaystyle [a, b]}$ liczb rzeczywistych $i$$\ Displaystyle P = (x_ {0}, x_ {1}, \ ldots,$ { a to znaczy partycja ${\ Displaystyle [a, b]$ za

$${\ Displaystyle a = x_ {0}<x_ {1}<x_ {2}<\ kropki <x_ {n} = b.}$$

Suma Riemanna z fa $\ displaystyle$$f}$ nad $b]}$ z partycją jest zdefiniowana jako ${\ displaystyle P}$

$${\ Displaystyle S = \ suma _ {i = 1} ^ {n} f (x_ {i} ^ {*}) \, \ Delta x_ {I},}$$

gdzie ${\ Displaystyle \ Delta x_ {i} = x_ {i} -x_ {i-1}}$ i ${\ styl wyświetlania x_{i}^{*}\w [x_{i-1},x_{i}]}$ . Można by uzyskać różne sumy Riemanna w zależności od tego $,$ wybrane W końcu nie będzie to miało znaczenia, jeśli funkcja jest Całkowalna Riemanna , gdy $zera$ szerokość sum zbliża się do

Typy sum Riemanna

Konkretne wybory dają różne typy sum Riemanna: ${\ displaystyle x_ {i} ^ {*}}$

• Jeśli $_$ metoda lewą regułą i . _ _
• Jeśli dla wszystkich $jest$ , metoda właściwą regułą Riemanna
• Jeśli ${\ Displaystyle x_ {i} ^ {*} = (x_ {i} + x_ {i-1})/2}$ dla wszystkich ja , metoda jest regułą punktu środkowego i daje środkową sumę Riemanna .
• fa ${\ Displaystyle f (x_ {i} ^ {*}) = \ sup f ([x_ {i-1}, x_$ (to znaczy supremum f nad ${\ Displaystyle [x_ {i-1}, x_ {i}]} )$ , metoda jest górną regułą i daje jakiś górna suma Riemanna lub górna suma Darboux .
• fa $(x_ {i} ^ {*}) = \ inf f ([x_ {i-1}, x_ { i}])}$ (czyli infimum f nad $}, x_ {i}]} )$ 1 , metoda jest niższą regułą i daje A niższa suma Riemanna lub niższa suma Darboux .

Wszystkie te metody sumowania Riemanna należą do najbardziej podstawowych sposobów całkowania numerycznego . Mówiąc luźno, funkcja jest całkowalna Riemanna , jeśli wszystkie sumy Riemanna zbiegają się, gdy podział „staje się coraz drobniejszy”.

Chociaż nie jest wyprowadzana jako suma Riemanna, przyjęcie średniej lewej i prawej sumy Riemanna jest regułą trapezów i daje sumę trapezów . Jest to jeden z najprostszych z bardzo ogólnych sposobów aproksymacji całek za pomocą średnich ważonych. Po tym następuje w złożoności reguła Simpsona i wzory Newtona-Cotesa .

Dowolna suma Riemanna na danym podziale (to znaczy dla dowolnego wyboru między ${i-1}$ - $displaystyle$ i $\ displaystyle x_{i}}$ ) jest zawarta między dolną i górną sumą Darboux. Stanowi to podstawę całki Darboux , która ostatecznie jest równoważna całce Riemanna.

Metody sumowania Riemanna

Do czterech metod sumowania Riemanna zwykle najlepiej stosować podprzedziały o równej wielkości. Przedział [ za , b ] jest zatem podzielony na $z których$ każdy ma długość

$${\ Displaystyle \ Delta x = {\ Frac {ba} {n}}.}$$

Punkty w podziale będą wtedy

$${\ Displaystyle a, \; a + \ Delta x, \; a + 2 \ Delta x, \; \ ldots, \; a + (n-2) \ Delta x, \; a + (n-1) \ Delta x, \;B.}$$

Reguła lewicy

Lewa suma Riemanna x ↦ x ³ przez [0, 2] przy użyciu 4 podprzedziałów

W przypadku lewej reguły funkcja jest aproksymowana przez jej wartości w lewych punktach końcowych podprzedziałów. Daje to wiele prostokątów o podstawie Δ x i wysokości f ( a + i Δ x ) . Zrobienie tego dla i = 0, 1, ..., n − 1 i zsumowanie uzyskanych obszarów daje

$${\ Displaystyle S _ {\ operatorname {lewo}} = \ Delta x \ lewo [f (a) + f (a + \ Delta x) + f (a + 2 \ Delta x) + \ kropki + f (b- \ Delta x)\prawo].}$$

Lewa suma Riemanna jest przeszacowaniem, jeśli f maleje monotonicznie w tym przedziale, i niedoszacowaniem, jeśli rośnie monotonicznie . Błąd tej formuły będzie

$${\ Displaystyle \ lewo \ vert \ int _ {a} ^ {b} f (x) \, dx-S _ {\ operatorname {lewo}} \ prawo \ vert \ leq {\frac {M_{1}(ba)^{2}}{2n}},}$$

gdzie $}$ maksymalną wartością wartości w przedziale $M_ {1}$ Displaystyle

Właściwa reguła

Prawa suma Riemanna x ↦ x ³ przez [0, 2] przy użyciu 4 podprzedziałów

Dla właściwej reguły funkcja jest aproksymowana przez jej wartości na prawych końcach podprzedziałów. Daje to wiele prostokątów o podstawie Δ x i wysokości f ( a + i Δ x ) . Zrobienie tego dla i = 1, ..., n i zsumowanie uzyskanych obszarów daje

$${\ Displaystyle S _ {\ operatorname {po prawej}} = \ Delta x \ lewo [f (a + \ Delta x) + f (a + 2 \ Delta x) + \ kropki + f (b) \ prawo].}$$

Właściwa suma Riemanna jest niedoszacowaniem, jeśli f jest monotonicznie malejące , i przeszacowaniem, jeśli jest monotonicznie rosnące . Błąd tej formuły będzie

$${\ Displaystyle \ lewo \ vert \ int _ {a} ^ {b} f (x) \, dx-S _ {\ operatorname {po prawej}} \ prawo \ vert \ leq {\frac {M_{1}(ba)^{2}}{2n}},}$$

gdzie $}$ maksymalną wartością wartości w przedziale $M_ {1}$ Displaystyle

Reguła punktu środkowego

Średnia suma Riemanna x ↦ x ³ w [0, 2] przy użyciu 4 podprzedziałów

W przypadku reguły punktu środkowego funkcja jest aproksymowana przez jej wartości w punktach środkowych podprzedziałów. Daje to f ( a + Δ x /2) dla pierwszego podprzedziału, f ( a + 3Δ x /2) dla następnego i tak dalej, aż do f ( b - Δ x /2) . Sumowanie uzyskanych obszarów daje

$${\ Displaystyle S _ {\ operatorname {mid}} = \ Delta x \ lewo [f \ lewo (a + {\ tfrac {\ Delta x} {2}} \ prawo) + f \ lewo (a + {\ tfrac {3 \ Delta x}{2}}\right)+\kropki +f\left(b-{\tfrac {\Delta x}{2}}\right)\right].}$$

Błąd tej formuły będzie

$${\ Displaystyle \ lewo \ vert \ int _ {a} ^ {b} f (x) \, dx-S _ {\ operatorname {środek}} \ prawo \ vert \leq {\frac {M_{2}(ba)^{3}}{24n^{2}}},}$$

gdzie jest maksymalną wartością wartości bezwzględnej w przedziale fa ${\ Displaystyle f ^ {\ pierwsza \ pierwsza}$$)$ Ten błąd jest o połowę mniejszy od sumy trapezowej; jako taka środkowa suma Riemanna jest najdokładniejszym podejściem do sumy Riemanna.

Reguła trapezowa

Główny artykuł: Reguła trapezów

Trapezoidalna suma x ↦ x ³ przez [0, 2] przy użyciu 4 podprzedziałów

W przypadku reguły trapezów funkcja jest aproksymowana przez średnią jej wartości na lewym i prawym końcu podprzedziału. $_$ wzoru b _{_} 1 _ _ _ _ ₂ , i wysokość h , a zsumowanie otrzymanych obszarów daje

$${\ Displaystyle S _ {\ operatorname {pułapka}} = {\ tfrac {1} {2}} \ Delta x \ lewo [f (a) + 2f (a + \ Delta x) + 2f (a + 2 \ Delta x) +\kropki +f(b)\prawo].}$$

Błąd tej formuły będzie

$${\ Displaystyle \ lewo \ vert \ int _ {a} ^ {b} f (x) \, dx-S _ {\ operatorname {pułapka}} \ prawo \ vert \leq {\frac {M_{2}(ba)^{3}}{12n^{2}}},}$$

gdzie jest maksymalną wartością wartości bezwzględnej $x)}$$($ .

Przybliżenie uzyskane za pomocą sumy trapezowej dla funkcji jest takie samo, jak średnia sum lewej i prawej strony tej funkcji.

Połączenie z integracją

Dla jednowymiarowej sumy Riemanna w domenie , gdy maksymalny rozmiar podprzedziału zmniejsza się do zera (to jest granica normy podprzedziałów dąży do zera), [ za , ${\ Displaystyle [a,$ niektóre funkcje będą miały zbieżność wszystkich sum Riemanna do tej samej wartości. Ta wartość graniczna, jeśli istnieje, jest zdefiniowana jako określona całka Riemanna funkcji w dziedzinie,

$${\ Displaystyle \ int _ {a} ^ {b} f (x) \, dx = \ lim _ {\|\ Delta x \|\ rightarrow 0} \ suma _ {i = 1} ^ {n} f ( x_{i}^{*})\,\Delta x_{i}.}$$

W przypadku domeny o skończonych rozmiarach, jeśli maksymalny rozmiar podprzedziału zmniejsza się do zera, oznacza to, że liczba podprzedziałów dąży do nieskończoności. W przypadku skończonych podziałów sumy Riemanna są zawsze przybliżeniem wartości granicznej, a przybliżenie to staje się lepsze, gdy podział staje się drobniejszy. Poniższe animacje pomagają zademonstrować, w jaki sposób zwiększenie liczby podprzedziałów (przy jednoczesnym obniżeniu maksymalnego rozmiaru podprzedziału) lepiej przybliża „obszar” pod krzywą:

• 

  Lewa suma Riemanna

• 

  Właściwa suma Riemanna

• 

  Średnia suma Riemanna

Ponieważ zakłada się tutaj, że czerwona funkcja jest funkcją gładką, wszystkie trzy sumy Riemanna będą zbiegać się do tej samej wartości, gdy liczba podprzedziałów dąży do nieskończoności.

Przykład

Porównanie prawej sumy Riemanna z całką x ↦ x ² po [0, 2].

Wizualna reprezentacja pola pod krzywą y = x ² nad [0, 2]. Używając funkcji pierwotnych, obszar ten wynosi dokładnie 8/3.

Przybliżanie pola pod krzywą y = x ² nad [0, 2] przy użyciu prawej sumy Riemanna. Zauważ, że ponieważ funkcja jest rosnąca monotonicznie, właściwa suma Riemanna zawsze przeszacuje obszar wniesiony przez każdy składnik sumy (i zrobi to maksymalnie).

Wartość prawej sumy Riemanna x ↦ x ² nad [0, 2]. Wraz ze wzrostem liczby prostokątów zbliża się do dokładnego obszaru 8/3.

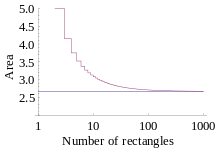
Biorąc przykład, pole pod krzywą y = x ² nad [0, 2] można obliczyć proceduralnie za pomocą metody Riemanna.

Przedział [0, 2] jest najpierw dzielony na n podprzedziałów, z których każdy ma określoną szerokość ${\ displaystyle {\ tfrac {2} {n}}}$ ; są to szerokości prostokątów Riemanna (zwanych dalej „pudełkami”). Ponieważ ma być użyta właściwa suma Riemanna, sekwencja x dla pudełek będzie następować ${\ Displaystyle x_ {1}, x_ {2}, \ ldots, x_ {n} }$ . Dlatego sekwencja wysokości pudełek będzie wynosić ${\ Displaystyle x_ {1} ^ {2}, x_ {2} ^ {2}, \ ldots, x_ {n} ^ {2}}$ . Jest to ważny fakt, że $}$$} {n}$ { i} .

Powierzchnia każdego pudełka będzie wynosić ${\ Displaystyle {\ tfrac {2} {n}} \ razy x_ {i} ^ {2}}$ i dlatego n -ta prawa suma Riemanna będzie wynosić:

$${\ Displaystyle {\ rozpocząć {wyrównane} S & = {\ Frac {2} {n}} \ lewo ({\ Frac {2} {n}} \ prawo) ^ {2} + \ kropki + {\ Frac {2 }{n}}\left({\frac {2i}{n}}\right)^{2}+\kropki +{\frac {2}{n}}\left({\frac {2n}{n }}\right)^{2}\\[1ex]&={\frac {8}{n^{3}}}\left(1+\dots +i^{2}+\dots +n^{ 2}\right)\\[1ex]&={\frac {8}{n^{3}}}\left({\frac {n(n+1)(2n+1)}{6}}\ prawo)\\[1ex]&={\frac {8}{n^{3}}}\left({\frac {2n^{3}+3n^{2}+n}{6}}\prawo )\\[1ex]&={\frac {8}{3}}+{\frac {4}{n}}+{\frac {4}{3n^{2}}}.\end{aligned} }}$$

Jeśli przyjąć granicę jako n → ∞, można stwierdzić, że przybliżenie zbliża się do rzeczywistej wartości pola pod krzywą wraz ze wzrostem liczby pudełek. Stąd:

$${\ Displaystyle \ lim _ {n \ do \ infty} S = \ lim _ {n \ do \ infty} \ lewo ({\ Frac {8} {3}} + {\ Frac {4} {n}} + {\frac {4}{3n^{2}}}\right)={\frac {8}{3}}.}$$

Ta metoda jest zgodna z całką oznaczoną obliczoną w bardziej mechaniczny sposób:

$${\ Displaystyle \ int _ {0} ^ {2} x ^ {2} \, dx = {\ Frac {8} {3}}.}$$

Ponieważ funkcja jest ciągła i monotonicznie rosnąca w przedziale, prawa suma Riemanna przeszacowuje całkę o największą wartość (podczas gdy lewa suma Riemanna niedoszacowałaby całki o największą wartość). Ten fakt, intuicyjnie widoczny na wykresach, pokazuje, w jaki sposób charakter funkcji determinuje dokładność szacowania całki. Chociaż proste, prawe i lewe sumy Riemanna są często mniej dokładne niż bardziej zaawansowane techniki szacowania całki, takie jak reguła trapezów lub reguła Simpsona .

Przykładowa funkcja ma łatwą do znalezienia funkcję pierwotną, więc oszacowanie całki za pomocą sum Riemanna jest głównie ćwiczeniem akademickim; należy jednak pamiętać, że nie wszystkie funkcje mają funkcje pierwotne, więc szacowanie ich całek przez sumowanie jest praktycznie ważne.

Wyższe wymiary

Podstawową ideą sumy Riemanna jest „rozbicie” domeny poprzez podział na części, pomnożenie „rozmiaru” każdego elementu przez pewną wartość, jaką funkcja przyjmuje na tym kawałku, i zsumowanie wszystkich tych iloczynów. Można to uogólnić, aby umożliwić sumy Riemanna dla funkcji w dziedzinach o więcej niż jednym wymiarze.

Chociaż intuicyjnie proces podziału domeny jest łatwy do uchwycenia, szczegóły techniczne tego, w jaki sposób można podzielić domenę, stają się znacznie bardziej skomplikowane niż przypadek jednowymiarowy i obejmują aspekty geometrycznego kształtu domeny.

Dwa wymiary

W dwóch wymiarach domenę można podzielić na liczbę dwuwymiarowych komórek $,$ że $textstyle A = \ bigcup _$$\$ . Każdą komórkę można wtedy zinterpretować jako mającą „obszar” oznaczony przez ${\ displaystyle \ Delta A_ {i}}$ . Dwuwymiarowa suma Riemanna to

$${\ Displaystyle S = \ suma _ {i = 1} ^ {n} f (x_ {i} ^ {*}, y_ {i}^{*})\,\Delta A_{i},}$$

gdzie ${\ Displaystyle (x_ {i} ^ {*}, y_ {i} ^ {*}) \ w A_ {i}}$ .

Trzy wymiary

W trzech wymiarach domena jest podzielona na pewną liczbę trójwymiarowych komórek tak, że $V$$textstyle$$V = \ bigcup _$ . Każdą komórkę można wtedy zinterpretować jako mającą „objętość” oznaczoną przez ${\ displaystyle \ Delta V_ {i}}$ . Trójwymiarowa suma Riemanna to

$${\ Displaystyle S = \ suma _ {i = 1} ^ {n} f (x_ {i} ^ { *},y_{i}^{*},z_{i}^{*})\,\Delta V_{i},}$$

gdzie ${\ Displaystyle (x_ {i} ^ {*}, y_ {i} ^ {*}, z_ {i} ^ {*}) \ w V_{i}}$ .

Dowolna liczba wymiarów

Wyższe wymiarowe sumy Riemanna mają podobny wzór. N - wymiarowa suma Riemanna to

$${\ Displaystyle S = \ suma _ {i} f (P_ {i} ^ {*}) \ \ Delta V_ {i},}$$

gdzie $i}}$${$ , czyli jest to punkt w n -wymiarowej komórce z n -wymiarowa objętość ${\ Displaystyle \ Delta V_ {i}}$ .

Uogólnienie

W dużej ogólności można zapisać sumy Riemanna

$${\ Displaystyle S = \ suma _ {i} f (P_ {i} ^ {*}) \ mu (V_ {i}),}$$

gdzie ${\ Displaystyle P_ {i} ^ {*}}$ oznacza dowolny dowolny punkt zawarty w zbiorze $P_ {i} ^ {* }}$ jest miarą zbioru podstawowego P ja $\ Displaystyle$ . Z grubsza mówiąc , miara to funkcja, która daje „rozmiar” zbioru, w tym przypadku $;$ w jednym wymiarze można to często interpretować jako długość, w dwóch wymiarach jako powierzchnię, w trzech wymiarach jako objętość i tak dalej.

Zobacz też

• funkcja pierwotna
• Metoda Eulera i metoda punktu środkowego , pokrewne metody rozwiązywania równań różniczkowych
• Całka Lebesgue'a
• Całka Riemanna , granica sum Riemanna, gdy podział staje się nieskończenie drobny
• Reguła Simpsona , potężna metoda numeryczna, potężniejsza niż podstawowe sumy Riemanna, a nawet reguła trapezów
• Reguła trapezów , metoda numeryczna oparta na średniej lewej i prawej sumy Riemanna

Linki zewnętrzne

• Weisstein, Eric W. „Suma Riemanna” . MathWorld .
• Symulacja pokazująca zbieżność sum Riemanna