Słowniczek prawdopodobieństwa i statystyki
Ten słownik statystyki i prawdopodobieństwa jest listą definicji terminów i pojęć używanych w naukach matematycznych statystyki i prawdopodobieństwa , ich poddyscyplinach i dziedzinach pokrewnych. Dodatkowe powiązane terminy można znaleźć w Słowniczku matematyki i Słowniczku projektowania eksperymentów .
| Statystyka |
|---|
 |
| Prawdopodobieństwo |
|---|
 |
A
- dopuszczalne reguły decyzyjne
- algebra zmiennych losowych
- alternatywna hipoteza
- analiza wariancji
- zdarzenie atomowe
- Inna nazwa zdarzenia elementarnego .
B
- wykres słupkowy
- Twierdzenie
- Bayesa
- Estymator Bayesa
- Czynnik Bayesa Błąd
- wnioskowania bayesowskiego
- 1. Każda cecha próby , która nie jest reprezentatywna dla większej populacji .
- 2. Różnica między wartością oczekiwaną estymatora a wartością prawdziwą.
- dane binarne
- Dane, które mogą przyjmować tylko dwie wartości, zwykle reprezentowane przez cyfry binarne 0 i 1.
- rozkład
- dwumianowy analiza dwuwymiarowa
- Rodzaj ilościowej analizy statystycznej, w której dokładnie dwie zmienne są analizowane w celu określenia empirycznego związku między nimi. Kontrastowa analiza wielowymiarowa .
- blocking (blokowanie)
- W projekcie eksperymentalnym rozmieszczenie jednostek eksperymentalnych w grupy („bloki”), które są do siebie podobne. Blokowanie jest często używane do zarządzania problemem pseudoreplikacji .
- Wykres pudełkowy
- metody Boxa-Jenkinsa
C
- badanie przyczynowe
- Badanie statystyczne, którego celem jest zmierzenie wpływu pewnej zmiennej na wynik innej zmiennej. Na przykład badanie przyczynowe może zadać pytanie: „Jak będzie się czuł mój ból głowy, jeśli wezmę aspirynę, w porównaniu do tego, czy nie wezmę aspiryny?” Badania przyczynowe mogą być eksperymentalne lub obserwacyjne.
- centralne twierdzenie graniczne
- moment centralny
- funkcja charakterystyczna
- rozkład chi-kwadrat
- test chi-kwadrat
- analiza skupień
- próbkowanie skupień
- zdarzenie komplementarne
- całkowicie losowy projekt
- statystyka obliczeniowa
- Badanie metod statystycznych, które są możliwe dzięki zastosowaniu metod obliczeniowych na styku statystyki i informatyki .
- towarzyszące
- W badaniu statystycznym wszelkie zmienne, na których wartości nie mają wpływu zabiegi eksperymentalne, takie jak wiek jednostki, płeć i poziom cholesterolu przed rozpoczęciem eksperymentalnej diety.
- rozkład warunkowy
- Biorąc pod uwagę dwie zmienne losowe o rozkładzie łącznym X i Y , warunkowy rozkład prawdopodobieństwa Y przy danym X (zapisanym „ Y | X ") jest rozkładem prawdopodobieństwa Y , gdy wiadomo, że X jest określoną wartością.
- prawdopodobieństwo Prawdopodobieństwo jakiegoś zdarzenia A przy założeniu wystąpienia zdarzenia B. W zapisie matematycznym prawdopodobieństwo warunkowe zapisuje się P( A | B ), i odczytuje się „prawdopodobieństwo A , biorąc pod uwagę B ”.
- warunkowe
- przedział ufności (CI) rozkładu
- warunkowego prawdopodobieństwa
- W statystyce wnioskowania: zakres prawdopodobnych wartości dla jakiegoś nieznanego parametru , takiego jak średnia populacji , zdefiniowany jako przedział z dolną i górną granicą. Dokładne wartości tych granic są obliczane na podstawie wcześniej określonego poziomu ufności , wybrany przez badacza. Poziom ufności reprezentuje częstotliwość przedziałów, które w dłuższej perspektywie przechwytują prawdziwą wartość nieznanego parametru; tj. 95% przedziałów ufności obliczonych na 95% poziomie ufności zawiera wartość prawdziwą, podobnie dla innych poziomów ufności. Na przykład, na podstawie badania nawyków związanych ze snem na losowej próbie 100 osób, badacz może oszacować na poziomie ufności 95%, że cała populacja śpi od 5 do 9 godzin na dobę. Istnieje 95% szans, że prawdziwa średnia populacji mieści się w tym przedziale, ponieważ 95% losowych próbek pobranych z tej samej populacji da 95% przedziały ufności, które zawierają prawdziwą średnią.
- poziom zaufania
- Liczba wskazująca prawdopodobieństwo, że przedział ufności (zakres) oddaje prawdziwą średnią populacji . Na przykład przedział ufności z 95% poziomem ufności ma 95% szans na uchwycenie średniej populacji. Z technicznego punktu widzenia oznacza to, że gdyby eksperyment był powtarzany wiele razy, 95% CI obliczonych na tym poziomie zawierałoby prawdziwą średnią populacji.
- confounder
- Zmienna , która wpływa zarówno na zmienną zależną , jak i na zmienną niezależną , powodując fałszywe skojarzenie. Istnienie ukrytych zmiennych zakłócających jest ważnym ilościowym wyjaśnieniem korelacji nie implikuje związku przyczynowego: jeśli zmiany w dwóch zmiennych wydają się być skorelowane, ryzykowne jest zakładanie, że jedna zmiana powoduje drugą, ponieważ jest możliwe, że jeden lub więcej niezidentyfikowanych czynników zakłócających w rzeczywistości spowodowało zmiany w obu zmiennych. Klasycznym przykładem jest korelacja między zwiększoną konsumpcją lodów a zwiększoną przestępczością latem. Irracjonalne jest zakładanie, że jedzenie większej ilości lodów powoduje, że ludzie popełniają więcej przestępstw lub odwrotnie; bardziej prawdopodobne jest, że jedna lub więcej dodatkowych zmiennych, np. cieplejsza pogoda, jednocześnie zwiększa zarówno spożycie lodów, jak i przestępczość. W tym przykładzie cieplejsza pogoda jest czynnikiem zakłócającym.
- koniugat przed
- ciągła zmienna
- korelacja
- próbkowania wygody
- Liczbowa miara siły zależności liniowej między dwiema zmiennymi losowymi (można ją wykorzystać do ilościowego określenia, na przykład, jak rozmiar buta i wzrost są skorelowane w populacji). Przykładem jest współczynnik korelacji iloczynu Pearsona , który można znaleźć dzieląc kowariancję dwóch zmiennych przez iloczyn ich odchyleń standardowych . Zmienne niezależne mają z definicji korelację równą 0. Korelacja populacyjna jest często reprezentowana przez symbol a korelacja próbki przez .</ref>
- dane zliczania
- Dane wynikające z liczenia , które w związku z tym mogą przyjmować tylko nieujemne wartości całkowite .
- kowariancja
- Biorąc pod uwagę dwie zmienne losowe X i Y , z wartościami oczekiwanymi i } wartość zmiennej losowej , zapisane w notacji statystycznej jako . Kowariancja jest używana do pomiaru korelacji ; można to interpretować jako stopień, w jakim dwie zmienne zmieniają się jednocześnie ze sobą lub „współzmienne”.
D
- dane
- analiza
- danych zestaw
- danych Próbka i powiązane punkty danych .
- punkt danych
- Wpisany pomiar — może to być wartość logiczna , liczba rzeczywista, wektor (w takim przypadku nazywany jest również wektorem danych ) itp.
- reguła decyzyjna
- teoria decyzji
- stopnie swobody
- oszacowanie gęstości
- zależność
- zmienna zależna
- statystyka opisowa
- projekt eksperymenty
- odchylenie
- wykres kropkowy
- zmiennej dyskretnej
- podwójne liczenie
mi
- zdarzenie elementarne
- Zdarzenie, które zawiera tylko jeden wynik w przestrzeni próbki ; w zbiorze możliwości, możliwość, która może wystąpić dokładnie w jeden sposób. Na przykład podczas wyciągania karty ze standardowej talii kart do gry „wyciąganie waleta pik” jest zdarzeniem elementarnym (ponieważ w całej talii jest tylko jeden walet pik), podczas gdy „wyciąganie króla lub asa” nie jest (ponieważ w talii są połączone cztery króle i cztery asy).
- teoria estymacji
- Dział statystyki zajmujący się estymacją wartości parametrów na podstawie zmierzonych danych empirycznych z elementem losowym . Parametry opisują podstawowe ustawienie fizyczne w taki sposób, że ich wartości wpływają na rozkład mierzonych danych; estymator próbuje wykorzystać pomiary do przybliżenia nieznanych parametrów .
- estymator
- Funkcja znanych danych używana do oszacowania nieznanego parametru ; oszacowanie jest wynikiem faktycznego zastosowania funkcji do określonego zestawu danych. Na przykład średnia może służyć jako estymator.
- wartość oczekiwana
- Suma prawdopodobieństw każdego możliwego wyniku eksperymentu pomnożona przez odpowiadającą im wypłatę lub „wartość”. W ten sposób reprezentuje średnią kwotę, jaką „oczekuje się” wygranej na zakład, jeśli zakłady o identycznych kursach są powtarzane wiele razy. Na przykład oczekiwana wartość rzutu uczciwą sześciościenną kostką wynosi 3,5. Koncepcja jest intuicyjnie uogólnieniem średniej ważonej wszystkich możliwych wyników określonej procedury lub eksperymentu i może być postrzegana jako średnia arytmetyczna dużej liczby niezależnych realizacji eksperymentu. Oczekiwana wartość zmiennej losowej X jest zwykle jako E (X) dla operatora oczekiwań dla parametru .
- eksperyment
- Każda procedura, która może być powtarzana w nieskończoność i która ma dobrze zdefiniowany zestaw wyników.
- zdarzenie
- rodziny wykładniczej
- Podzbiór przestrzeni próbki procedury lub eksperymentu (tj. możliwego wyniku), któremu można przypisać prawdopodobieństwo. Na przykład przy rzucie kostką „wyrzucenie trójki” 1/3 ( jest zdarzeniem (z prawdopodobieństwem 1/6 z prawdopodobieństwem , jeśli kostka jest sprawiedliwa), podobnie jak „wyrzucenie piątki lub szóstki” ) .
F
- analiza czynnikowa
- eksperyment czynnikowy
- rozkład częstotliwości
- dziedzina
- częstotliwości
- wnioskowanie częstościowe
G
H
- histogram
- Przybliżone graficzne przedstawienie rozkładu danych liczbowych. Histogram przedstawia ten rozkład, dzieląc cały zakres wartości na serię kolejnych, nienakładających się przedziałów, a następnie zliczając, ile wystąpień zbioru danych mieści się w każdym przedziale.
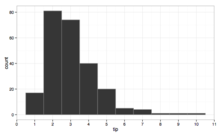
Histogram przedstawiający rozkład napiwków wydawanych w restauracji
I
- niezależna
- zmienna niezależna
- rozstęp międzykwartylowy (IQR)
- Miara rozproszenia statystycznego zbioru danych, zdefiniowana jako różnica między 25. a 75. percentylem danych. Aby obliczyć lub kwartyle uporządkowane rangi, których granice na 25, 50 i 75 percentylu są 2 i odpowiednio 3 ; IQR = 3 1 .
J
- wspólny rozkład
- Przy danych dwóch zmiennych losowych X i Y , wspólny rozkład X i Y jest rozkładem prawdopodobieństwa X i Y razem.
- wspólne prawdopodobieństwo
- Prawdopodobieństwo wystąpienia dwóch zdarzeń jednocześnie. Łączne prawdopodobieństwo A i B jest zapisywane lub .
k
- Kurtoza
- oszacowania gęstości jądra
- filtra
- Kalmana
- Miara „ogoniastości” rozkładu prawdopodobieństwa zmiennej losowej o wartościach rzeczywistych. Istnieją różne sposoby kwantyfikowania, szacowania i interpretowania kurtozy, ale powszechna interpretacja jest taka, że kurtoza reprezentuje stopień, w jakim na kształt rozkładu wpływają rzadkie skrajne obserwacje ( wartości odstające ); w tym przypadku wyższa kurtoza oznacza, że większa część wariancji wynika z rzadkich skrajnych odchyleń, w przeciwieństwie do częstych odchyleń o niewielkich rozmiarach.
Ł
- Prawo wielkich liczb (LLN)
- momentu L
- Twierdzenie, zgodnie z którym średnia wyników uzyskanych z wykonywania tego samego eksperymentu dużą liczbę razy powinna być bliska wartości oczekiwanej eksperymentu i ma tendencję do zbliżania się do wartości oczekiwanej jako przeprowadza się więcej prób. Prawo sugeruje, że konieczna jest wystarczająco duża liczba prób, aby wyniki dowolnego eksperymentu można było uznać za wiarygodne, a co za tym idzie, wykonanie tylko niewielkiej liczby prób może skutkować niepełną lub wprowadzającą w błąd interpretacją wyników eksperymentu.
- funkcja prawdopodobieństwa
- Warunkowa funkcja prawdopodobieństwa rozpatrywana jako funkcja drugiego argumentu z ustalonym pierwszym argumentem. Na przykład wyobraź sobie, że wyciągasz ponumerowaną kulę o liczbie k z worka zawierającego n kul, ponumerowanych od 1 do n ; funkcję prawdopodobieństwa dla zmiennej losowej N można opisać jako prawdopodobieństwo wyciągnięcia k przy założeniu, że istnieje n piłek: prawdopodobieństwo wyniesie 1/ n dla n większych lub równych k oraz 0 dla n mniejszych niż k . W przeciwieństwie do funkcji rozkładu prawdopodobieństwa, ta funkcja prawdopodobieństwa nie sumuje się do 1 w przestrzeni próbki .
- test ilorazu wiarygodności
- funkcji straty

Wykres ilustrujący prawo wielkich liczb : zaobserwowane wyniki wielokrotnego rzucania uczciwą kostką (zielona linia) szybko zbliżają się do teoretycznej oczekiwanej wartości pojedynczego rzutu (niebieska linia) wraz ze wzrostem liczby rzutów kostką
M
- Rozkład krańcowy
- estymatora M
- Mając dwie zmienne losowe X i Y o rozkładzie łącznym , rozkład krańcowy X jest po prostu rozkładem prawdopodobieństwa X , gdy informacje o Y są ignorowane.
- krańcowe prawdopodobieństwo
- krańcowe
- prawdopodobieństwo Prawdopodobieństwo danego zdarzenia, pomijając wszelkie informacje o innych zdarzeniach. Krańcowe prawdopodobieństwo A jest zapisywane jako P ( A ). Kontrast prawdopodobieństwo warunkowe .
- Łańcuch Markowa Monte Carlo
- statystyka matematyczna
- oszacowanie największej wiarygodności
- średnia
- 1. Wartość oczekiwana zmiennej losowej.
- 2. Średnia arytmetyczna , czyli średnia matematyczna zbioru wartości liczbowych, obliczona przez podzielenie sumy wartości przez liczbę wartości.
- mediana mediana
- trybu
- odchylenia bezwzględnego
- średnia ruchoma
- Szereg średnich matematycznych lub średnich różnych podzbiorów większego zbioru danych, zwykle obliczanych w celu zrozumienia trendów w zbiorze danych w czasie.
- rozkład multimodalny
- analiza wielowymiarowa
- wielowymiarowa estymacja gęstości jądra
- wielowymiarowa zmienna losowa
- Wektor, którego składowymi są zmienne losowe w tej samej przestrzeni prawdopodobieństwa.
- wzajemna wyłączność
- wzajemna niezależność
- O zbiorze zdarzeń mówi się, że są wzajemnie niezależne jeśli dla dowolnego podzbioru zbioru łączne prawdopodobieństwo wszystkich zachodzących zdarzeń jest równe iloczynowi łącznych prawdopodobieństw poszczególnych zdarzeń. Pomyśl o wyniku serii rzutów monetą. Jest to warunek silniejszy niż niezależność par.
N
- regresja nieparametryczna
- statystyka nieparametryczna
- błąd niepróbkowania
- rozkład normalny
- wykres prawdopodobieństwa normalnego
- 0 hipoteza zerowa (H )
- Stwierdzenie testowane w teście istotności statystycznej ; zwykle stwierdzenie „brak efektu” lub „brak różnicy”. Na przykład w teście, czy światło ma wpływ na sen, hipoteza zerowa byłaby taka, że światło nie ma wpływu na sen (tj. wzorce snu są takie same niezależnie od warunków oświetleniowych). Hipoteza zerowa jest wyrazem oczekiwania, że zmienna zależna nie zmieni się znacząco w miarę modyfikacji zmiennej niezależnej ; istotność statystyczna jest mierzona i raportowana zgodnie ze stopniem spełnienia tego oczekiwania. Porównaj hipotezę alternatywną .
O
P
- niezależność parami
- wartości p
- Zbiór zmiennych losowych, z których dowolne dwie są niezależne.
- parametr Każda zmierzona wielkość
- populacji statystycznej , która podsumowuje lub opisuje aspekt populacji, np. średnią lub odchylenie standardowe ; często ilość, którą należy oszacować na podstawie odpowiedniej ilości obliczonej przez pobranie losowych próbek z populacji. Może to być parametr populacji, parametr dystrybucji lub nieobserwowany parametr.
- wykres kołowy
- percentyla
- filtra cząstek stałych
- moc
- estymacji punktowej
- prawdopodobieństwo wcześniejsze
- We wnioskowaniu bayesowskim wcześniejsze przekonania lub inne informacje, które są dostępne przed wzięciem pod uwagę nowych danych lub obserwacji.
- parametr populacji
- Patrz parametr .
- prawdopodobieństwo późniejsze
- Wynik analizy bayesowskiej , który zawiera kombinację wcześniejszych przekonań lub informacji ( prawdopodobieństwo wcześniejsze ) z zaobserwowanymi danymi.
- analiza głównych składowych (PCA)
- gęstość
- prawdopodobieństwa prawdopodobieństwa
- Prawdopodobieństwo w ciągłym rozkładzie prawdopodobieństwa. Na przykład nie można powiedzieć, że prawdopodobieństwo, że mężczyzna ma sześć stóp wzrostu, wynosi 20%, ale można powiedzieć, że ma on 20% szans na to, że będzie miał od pięciu do sześciu stóp wzrostu. Gęstość prawdopodobieństwa jest określona przez funkcję gęstości prawdopodobieństwa . Masa prawdopodobieństwa kontrastu .
- funkcja gęstości prawdopodobieństwa
- Rozkład prawdopodobieństwa dla ciągłej zmiennej losowej.
- rozkład prawdopodobieństwa
- Funkcja dająca prawdopodobieństwo wystąpienia wszystkich elementów w danej przestrzeni; zobacz Lista rozkładów prawdopodobieństwa .
- miara prawdopodobieństwa
- Prawdopodobieństwo zdarzeń w przestrzeni prawdopodobieństwa .
- prawdopodobieństwo wykresu
- przestrzeń prawdopodobieństwa
- Przestrzeń próbki , w której zdefiniowano miarę prawdopodobieństwa .
Q
- kwantyl
- Określony punkt lub wartość, w której zakres rozkładu prawdopodobieństwa jest podzielony na ciągłe przedziały o równym prawdopodobieństwie lub w którym obserwacje w próbie są podzielone w ten sam sposób. Liczba grup, na które dzieli się zakres, jest zawsze o jeden większa niż liczba dzielących je kwantyli. Powszechnie używane kwantyle obejmują kwartyle (które dzielą zakres na cztery grupy), decyle (dziesięć grup) i percentyle (sto grup). Same grupy są określane jako połówki, tercje, ćwiartki itp., Chociaż terminy określające kwantyle są czasami używane w odniesieniu do grup, a nie do punktów odcięcia.
- kwartyl
- Rodzaj kwantyla , który dzieli zakres punktów danych na cztery równej wielkości grupy zwane ćwiartkami . Dla każdego zbioru danych podzielonego kwartylowo istnieją dokładnie trzy kwartyle lub punkty podziału, które tworzą cztery grupy. Pierwszy kwartyl ( jest zdefiniowany jako środkowy punkt danych lub wartość, która znajduje się w połowie odległości między najmniejszą wartością (minimum) a medianę zbioru danych, tak aby 25 procent danych znajdowało się poniżej tego kwartyla. Drugi kwartyl ( z 50 procentami danych poniżej tego punktu. Trzeci kwartyl ( jest definiowany jako środkowa wartość w połowie drogi między medianą a największą wartością (maksimum) zbioru danych, tak że 75 procent danych znajduje się poniżej tego kwartyla . Ponieważ dane muszą być uporządkowane od najmniejszego do największego, aby je obliczyć, kwartyle są rodzajem statystyki porządkującej .
- próbkowanie kwotowe
R
- zmienna losowa
- Mierzalna funkcja w przestrzeni prawdopodobieństwa, często o wartościach rzeczywistych. Funkcja dystrybucji zmiennej losowej daje prawdopodobieństwo różnych wartości zmiennej. Można również wyprowadzić średnią i wariancję zmiennej losowej. Zobacz także dyskretna zmienna losowa i ciągła zmienna losowa .
- randomized block design
- range
- Długość najmniejszego przedziału, który zawiera wszystkie dane.
- rekurencyjna estymacja bayesowska
- analiza regresji miary
- powtarzane projekt
- odpowiedzi zmienna
- Dowolna zmienna na których wartość ma wpływ eksperymentalna obróbka lub zmiany jednej lub większej liczby innych zmiennych lub oczekuje się, że zostaną one zmienione; np. poziom cholesterolu po przestrzeganiu określonej diety przez sześć miesięcy. Zmienne odpowiedzi to te, które zmieniają się lub reagują na pewne badane zjawisko. Termin ten jest często używany zamiennie ze zmienną zależną .
- ograniczona randomizacja
- solidne statystyki
- błąd zaokrąglenia
S
- próbka
- Ta część populacji , która jest faktycznie obserwowana.
- średnia kowariancji
- próbki
- Średnia arytmetyczna próbki wartości pobranej z populacji, zwykle oznaczana przez } . Przykładem jest średni wynik testu podzbioru 10 uczniów z klasy. Średnia z próby jest używana jako estymator średniej populacji, która w tym przykładzie byłaby średnim wynikiem testu wszystkich uczniów w klasie.
- miejsce na próbki
- Zbiór możliwych wyników eksperymentu. Na przykład przykładowe miejsce do rzucania sześcienną kostką będzie wynosić {1, 2, 3, 4, 5, 6}.
- próbkowanie
- Proces selekcji obserwacji w celu uzyskania wiedzy o populacji. Istnieje wiele metod wyboru próbki do przeprowadzenia obserwacji.
- próbkowanie odchylenia
- rozkład próbkowania
- Rozkład prawdopodobieństwa danej statystyki przy wielokrotnym próbkowaniu populacji.
- błąd próbkowania
- wykres punktowy
- skala parametru
- poziom istotności
- próba prosta próba losowa
- Paradoks Simpsona
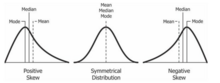
- skośność
- Miara asymetrii rozkładu prawdopodobieństwa zmiennej losowej o wartościach rzeczywistych względem jej średniej . Z grubsza mówiąc, rozkład ma skośność dodatnią (skośną w prawo), jeśli wyższy ogon jest dłuższy, i skośną ujemną (skośną w lewo), jeśli dolny ogon jest dłuższy. Idealnie symetryczne rozkłady zawsze mają zerową skośność, chociaż zerowa skośność niekoniecznie oznacza rozkład symetryczny.
- odchylenie standardowe
- wykresu spaghetti
- odchylenie standardowe
- Najczęściej stosowana miara rozproszenia statystycznego. Jest to pierwiastek kwadratowy z wariancji i jest ogólnie oznaczany małą grecką ( sigma .
- błąd standardowy
- statystyka
- wyniku standardowego
- Wynik zastosowania algorytmu statystycznego do zbioru danych. Można go również opisać jako obserwowalną zmienną losową.
- grafika
- statystyczna dyspersji statystycznej
- hipoteza statystyczna testująca
- niezależność statystyczną
- Dwa zdarzenia są niezależne, jeśli wynik jednego nie wpływa na wynik drugiego (na przykład wyrzucenie 1 w jednym rzucie kostką nie wpływa na prawdopodobieństwo wyrzucenia 1 w drugim rzucie). Podobnie, gdy twierdzimy, że dwie zmienne losowe są niezależne, intuicyjnie mamy na myśli, że wiedza o wartości jednej z nich nie daje żadnej informacji o wartości drugiej.
- wnioskowanie statystyczne
- Wnioskowanie o populacji oparte na losowej próbie pobranej z tej populacji lub, bardziej ogólnie, o losowym procesie na podstawie jej obserwowanego zachowania w skończonym okresie czasu.
- model statystyczny
- populacja statystyczna
- Zbiór jednostek, na temat których należy wyciągnąć wnioski statystyczne, często w oparciu o losowe pobieranie próbek. Można też mówić o populacji miar lub wartości.
- dyspersja statystyczna
- Zmienność statystyczna jest miarą stopnia zróżnicowania niektórych danych. Można to wyrazić wariancją lub odchyleniem standardowym.
- Parametr parametr który indeksuje rodzinę rozkładów prawdopodobieństwa.
- statystyczny
- istotność statystyczna
- statystyka
- test t-Studenta
- wyświetlanie łodygi i liści losowanie
- warstwowe
- metodologia badania
- funkcja
- przeżycia błąd przeżywalności
- symetryczny rozkład prawdopodobieństwa
- systematyczne pobieranie próbek
T
u
V
W
X
Y
Z
Zobacz też
- Notacja w rachunku prawdopodobieństwa i statystyce
- Aksjomaty prawdopodobieństwa
- Słowniczek projektowania eksperymentalnego
- Lista tematów statystycznych
- Lista tematów prawdopodobieństwa
- Słowniczek dziedzin matematyki
- Słowniczek rachunku różniczkowego
Linki zewnętrzne
- „A Glossary of DOE Terminology” , NIST/SEMATECH e-Handbook of Statistical Methods , NIST , dostęp 28 lutego 2009 r .
- Glosariusz statystyczny , Statistics.com , pobrano 28 lutego 2009 r
- Prawdopodobieństwo i statystyki dotyczące najwcześniejszych stron zastosowań (Univ. of Southampton)