Wykres radarowy

„Wykres pająka” przekierowuje tutaj. Aby zapoznać się z rozszerzeniem diagramów Eulera, zobacz diagram Spidera .
Przykładowy wykres gwiazdowy z NASA, z niektórymi najbardziej pożądanymi wynikami projektu przedstawionymi pośrodku
Ten wykres pająka przedstawia przydzielony budżet w porównaniu z rzeczywistymi wydatkami danej organizacji.

Wykres radarowy to graficzna metoda wyświetlania danych wielowymiarowych w formie dwuwymiarowego wykresu trzech lub więcej zmiennych ilościowych przedstawionych na osiach rozpoczynających się od tego samego punktu. Względne położenie i kąt osi zazwyczaj nie dostarczają żadnych informacji, ale można zastosować różne heurystyki, takie jak algorytmy wykreślające dane jako maksymalny całkowity obszar, aby posortować zmienne (osie) we względne pozycje, które ujawniają wyraźne korelacje, kompromisy, i wiele innych miar porównawczych.

Mapa radarowa jest również nazywana mapą sieciową , mapą pająka , wykresem pająka , mapą pajęczej sieci , mapą gwiazd , wykresem gwiazd , mapą pajęczyny , nieregularnym wielokątem , mapą biegunową lub diagramem Kiviata . Jest to odpowiednik równoległego wykresu współrzędnych , z osiami ułożonymi promieniowo.

Przegląd

Mapa radarowa to wykres i/lub wykres składający się z sekwencji równokątnych ramion, zwanych promieniami, przy czym każdy słup reprezentuje jedną ze zmiennych. Długość danych szprychy jest proporcjonalna do wielkości zmiennej dla punktu danych w stosunku do maksymalnej wielkości zmiennej we wszystkich punktach danych. Rysowana jest linia łącząca wartości danych dla każdej szprychy. Daje to fabule wygląd przypominający gwiazdę i pochodzenie jednej z popularnych nazw tej fabuły. Wykres gwiazdowy można wykorzystać do odpowiedzi na następujące pytania:

  • Które obserwacje są najbardziej podobne, tj. czy istnieją skupiska obserwacji? (Wykresy radarowe służą do badania względnych wartości pojedynczego punktu danych (np. punkt 3 jest duży dla zmiennych 2 i 4, mały dla zmiennych 1, 3, 5 i 6) oraz do lokalizowania podobnych lub odmiennych punktów.)
  • Czy istnieją wartości odstające?

Wykresy radarowe są użytecznym sposobem wyświetlania obserwacji wielowymiarowych z dowolną liczbą zmiennych. Każda gwiazda reprezentuje pojedynczą obserwację. Zazwyczaj mapy radarowe są generowane w formacie wielowątkowym, z wieloma gwiazdami na każdej stronie, a każda gwiazda reprezentuje jedną obserwację. Wykres gwiazdowy został po raz pierwszy użyty przez Georga von Mayra w 1877 r. Wykresy radarowe różnią się od wykresów glifowych tym, że do skonstruowania wykresu gwiazdy wykorzystywane są wszystkie zmienne. Nie ma podziału na zmienne pierwszego planu i tła. Zamiast tego figury w kształcie gwiazdy są zwykle ułożone na stronie w prostokątny układ. Nieco łatwiej jest dostrzec wzorce w danych, jeśli obserwacje ułożone są w jakiejś niedowolnej kolejności (jeśli zmienne są przypisane do promieni gwiazdy w jakiejś znaczącej kolejności).

Aplikacje

Shohei Ohtani's batting stats vs MLB average batting stats
Wykres radarowy przedstawiający statystyki mrugnięć z sezonu MLB 2021. Shoehi Ohtani, zielony, przewyższa średnie w tym sezonie DH, czerwony i MLB, niebieski, ale także częściej uderza. Dane z https://www.baseball-reference.com/ .

Wykresy radarowe mogą być wykorzystywane w sporcie do przedstawiania mocnych i słabych stron zawodników poprzez obliczanie różnych statystyk związanych z zawodnikiem, które można śledzić wzdłuż centralnej osi wykresu. Przykładami mogą być oddane strzały, zbiórki, asysty itp. lub statystyki baseballisty dotyczące odbijania lub rzucania. Tworzy to scentralizowaną wizualizację mocnych i słabych stron gracza, a jeśli pokrywa się ze statystykami innych graczy lub średnimi ligowymi, może pokazać, gdzie zawodnik wyróżnia się, a gdzie może się poprawić. Te spostrzeżenia na temat mocnych i słabych stron zawodników mogą okazać się kluczowe dla rozwoju zawodników, ponieważ pozwalają trenerom i trenerom na dostosowanie planu treningowego zawodnika w celu poprawy jego słabych stron. Wyniki mapy radarowej mogą być również przydatne w grze sytuacyjnej. Jeśli okaże się, że pałkarz słabo uderza przeciwko miotaczom leworęcznym, jego zespół wie, że należy ograniczyć jego występy przeciwko miotaczom leworęcznym, podczas gdy drużyna przeciwna może próbować wymusić sytuację, w której pałkarz będzie zmuszony uderzyć miotacz.

The performance metrics of 3 different types of vehicle
Wykres radarowy przedstawiający różnice w parametrach wydajności sedana, samochodu sportowego i pickupa.

Innym zastosowaniem wykresów radarowych jest kontrola poprawy jakości w celu wyświetlania wskaźników wydajności różnych obiektów, w tym programów komputerowych, komputerów, telefonów, pojazdów i innych. Programiści komputerowi często korzystają z analiz, aby przetestować wydajność swoich programów w porównaniu z innymi. Przykładem zastosowania wykresów radarowych jest analiza wydajności różnych algorytmów sortowania. Programista może zebrać kilka różnych algorytmów sortowania, takich jak wybór, bąbelek i szybkie, a następnie przeanalizować wydajność tych algorytmów, mierząc ich prędkość, zużycie pamięci i zużycie energii, a następnie wykreślić je na wykresie radarowym, aby zobaczyć, jak działa każdy sort przy różnych rozmiarach danych. Innym zastosowaniem związanym z wydajnością jest mierzenie osiągów podobnych samochodów względem siebie. Konsument może przyjrzeć się zmiennym, takim jak maksymalna prędkość samochodu, mile na galon, moc i moment obrotowy. Następnie, po wykorzystaniu wykresu radarowego do wizualizacji danych, na podstawie wyników mogli zdecydować, który samochód będzie dla nich najlepszy.

Wykres radarowy pokazujący podobieństwo dwóch społeczności składających się z połączonych okien genomowych; zobacz mapowanie architektury genomu .

Wykresy radarowe mogą być wykorzystywane w naukach przyrodniczych do wyświetlania mocnych i słabych stron leków i innych leków. Na przykładzie dwóch leków przeciwdepresyjnych badacz może uszeregować zmienne, takie jak skuteczność, skutki uboczne, koszt itp., w skali od jednego do dziesięciu. Następnie mogli sporządzić wykres wyników za pomocą wykresu radarowego, aby zobaczyć rozkład zmiennych i dowiedzieć się, jakie są między nimi różnice, na przykład jeden lek przeciwdepresyjny jest tańszy i szybciej działający, ale nie zapewnia dużej ulgi w miarę upływu czasu. Tymczasem drugi lek przeciwdepresyjny zapewnia silniejszą ulgę i lepiej utrzymuje się w miarę upływu czasu, ale jest droższy. Kolejnym zastosowaniem w naukach przyrodniczych jest analiza pacjentów. Wykresy radarowe można wykorzystać do wykreślenia zmiennych życiowych wpływających na dobre samopoczucie danej osoby, a następnie przeanalizować je, aby im pomóc. Bardziej konkretnym przykładem jest przypadek sportowców, u których monitoruje się różne nawyki związane z dobrym samopoczuciem, takie jak sen, dieta i stres, aby mieć pewność, że pozostaną w szczytowej kondycji fizycznej. Jeśli jakiekolwiek obszary zostaną pokazane jako zanurzone, lekarze i trenerzy mogliby wkroczyć, aby pomóc sportowcowi i poprawić jego samopoczucie.

Ograniczenia

Wykresy radarowe nadają się przede wszystkim do uderzającego pokazywania wartości odstających i wspólnych lub gdy jeden wykres jest większy pod względem każdej zmiennej od drugiego i są używane głównie do pomiarów porządkowych – gdzie każda zmienna odpowiada pod pewnymi względami „lepiej”, a wszystkie zmienne znajdują się na tej samej skali .

Z drugiej strony wykresy radarowe były krytykowane jako słabo przystosowane do podejmowania decyzji kompromisowych – gdy jeden wykres jest większy od drugiego w przypadku niektórych zmiennych, ale mniej w przypadku innych.

Co więcej, trudno jest wizualnie porównać długości różnych szprych, ponieważ trudno jest ocenić odległości promieniowe, chociaż koncentryczne okręgi służą jako linie siatki. Zamiast tego można użyć prostego wykresu liniowego, szczególnie w przypadku szeregów czasowych.

Wykresy radarowe mogą w pewnym stopniu zniekształcać dane, zwłaszcza gdy obszary są wypełnione, ponieważ zawarty w nich obszar staje się proporcjonalny do kwadratu miar liniowych. Na przykład na wykresie zawierającym 5 zmiennych o wartościach od 1 do 100 obszar objęty wielokątem ograniczonym przez 5 punktów, gdy wszystkie miary wynoszą 90, jest o ponad 10% większy niż w przypadku wykresu ze wszystkimi wartościami 82.

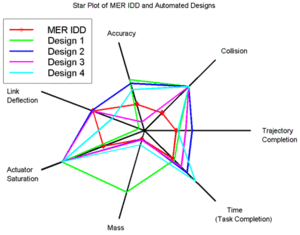
Wykresy radarowe mogą również być trudne do wizualnego porównania różnych próbek na wykresie, gdy ich wartości są blisko siebie, ponieważ ich linie lub obszary przenikają się, jak pokazano na rysunku 5.

Sztuczna struktura

Wykresy radarowe nakładają na dane kilka struktur, które często są sztuczne:

  • Pokrewieństwo sąsiadów – wykresy radarowe są często używane, gdy sąsiednie zmienne są niepowiązane, tworząc fałszywe połączenia.
  • Struktura cykliczna – pierwsza i ostatnia zmienna są umieszczone obok siebie.
  • Długość – zmienne są często w najbardziej naturalny sposób porządkowe: lepsze lub gorsze, chociaż stopień różnicy może być sztuczny.
  • Powierzchnia – powierzchnia skaluje się do kwadratu wartości, wyolbrzymiając efekt dużych liczb. Na przykład 2, 2 zajmuje 4 razy większą powierzchnię niż 1, 1. Jest to ogólny problem w przypadku wykresów warstwowych i trudno jest ocenić powierzchnię – patrz „Hierarchia Clevelanda”.

Na przykład naprzemienne dane 9, 1, 9, 1, 9, 1 dają wykres radarowy ze szczytami (który wchodzi i wychodzi), podczas gdy zmiana kolejności danych na 9, 9, 9, 1, 1, 1 zamiast tego daje dwa różne kliny (sektory).

W niektórych przypadkach istnieje naturalna struktura i mapy radarowe mogą być dobrze dopasowane. Na przykład w przypadku diagramów danych zmieniających się w cyklu 24-godzinnym dane godzinowe są w naturalny sposób powiązane z sąsiadami i mają strukturę cykliczną, dzięki czemu można je w naturalny sposób wyświetlić jako wykres radarowy.

Jeden zestaw wytycznych dotyczących korzystania z map radarowych (lub raczej ściśle powiązanego „wykresu biegunowego”) to:

  • nie masz nic przeciwko czytaniu ułożonych w stos obszarów zamiast pozycji według wspólnej skali (patrz Hierarchia Clevelanda),
  • zbiór danych jest rzeczywiście cykliczny, a nie liniowy, oraz
  • istnieją dwie serie do porównania, jedna znacznie mniejsza od drugiej

Rozmiar zestawu danych

zbiorów danych o małych i średnich rozmiarach . Ich podstawową słabością jest to, że ich skuteczność ogranicza się do zbiorów danych zawierających mniej niż kilkaset punktów. Potem mają tendencję do przytłaczania.

Co więcej, w przypadku korzystania z map radarowych zawierających wiele wymiarów lub próbek, mapa radarowa może stać się zaśmiecona i trudniejsza do interpretacji w miarę wzrostu liczby próbek.

Weźmy na przykład tabelę statystyk odbijania porównującą MVP MLB 2021 Shohei Ohtani ze statystykami przeciętnych wyznaczonych pałkarzy w lidze i niektórych graczy Hall of Fame. Te statystyki przedstawiają procent trafień, home runów, strike outów itp. przypadających na odbijanie gracza. Aby uzyskać więcej informacji na temat tego, co reprezentuje każda statystyka użyta w tabeli, możesz zapoznać się z tym odniesieniem przez MLB. Wykorzystamy poniższą tabelę do utworzenia wykresów radarowych porównujących statystyki odbijania MVP 2021 ze średnimi ligowymi dla wyznaczonych pałkarzy i zwykłych pałkarzy, próbując zwizualizować wskaźniki wydajności i wizualnie dojść do wniosku, że Shohei przewyższał przeciętnego gracza. Następnie umieścimy dodatkowe próbki na wykresie Radar, wykorzystując graczy Hall of Fame Jackie Robinson, Jim Thome i Frank Thomas do porównania Shohei z kilkoma najlepszymi pałkarzami wszechczasów. Ten wykres radarowy nie tylko może dać nam intuicję dotyczącą tego, jak Shohei wypada na tle czołowych graczy historycznych, ale także posłuży do pokazania ograniczeń wynikających z posiadania zbyt wielu próbek na wykresie radarowym.

Cel BA OBP SLG OPS HR% WIĘC% NOCLEG ZE ŚNIADANIEM%
MLB 0,244 0,317 0,411 0,728 0,037 0,232 0,087
DH 0,239 0,316 0,434 0,75 0,047 0,256 0,093
Shohei Ohtani 0,257 0,372 0,592 0,965 0,086 0,296 0,15
Jackie Robinsona 0,313 0,41 0,477 0,887 0,0282 0,0582 0,151
Jima Thome’a 0,276 0,402 0,554 0,956 0,072 0,302 0,207
Franka Thomasa 0,301 0,419 0,555 0,974 0,063 0,17 0,203

Na rysunku 10 możemy zobaczyć, jak można łatwo zinterpretować wykres radarowy, gdy liczba szprych i próbek jest stosunkowo mała. Kiedy porównujemy więcej próbek na rysunku 11, nawet bez wypełnienia obszaru na mapie radarowej, staje się jasne, jak trudna może być interpretacja lub podjęcie decyzji kompromisowych.

Przykład

Szczegółowy wątek gwiazdowy Cadillaca Seville

Wykres po prawej stronie zawiera wykresy gwiazdowe 15 samochodów . Lista zmiennych dla przykładowego wykresu gwiazdowego to:

  1. Cena
  2. Przebieg (MPG)
  3. Rekord napraw z 1978 r. (1 = najgorszy, 5 = najlepszy)
  4. Rekord napraw z 1977 r. (1 = najgorszy, 5 = najlepszy)
  5. Nad głową
  6. Pokój na tylnym siedzeniu
  7. Przestrzeń bagażnika
  8. Waga
  9. Długość

Możemy przyjrzeć się tym wykresom indywidualnie lub wykorzystać je do identyfikacji skupisk samochodów o podobnych cechach. Przykładowo, możemy spojrzeć na wykres gwiazdowy Cadillaca Seville (ostatniego na zdjęciu) i zobaczyć, że jest to jeden z najdroższych samochodów, pali poniżej średniego (ale nie najgorszego) przebiegu, ma przeciętne rekord napraw i ma średnią do ponadprzeciętnej przestronność i rozmiar. Wtedy będziemy mogli porównać Cadillaca modele (trzy ostatnie wykresy) z modelami AMC (pierwsze trzy wykresy). To porównanie pokazuje różne wzorce. Modele AMC są zazwyczaj niedrogie, zużywają mniej niż przeciętnie paliwa i są małe zarówno pod względem wysokości, masy, jak i przestronności. Modele Cadillaca są drogie, zużywają niewiele paliwa i są duże zarówno pod względem wielkości, jak i przestronności.

Alternatywy

Można używać wykresów liniowych dla szeregów czasowych i innych danych w postaci współrzędnych równoległych .

Do graficznego, jakościowego porównania dwuwymiarowych danych tabelarycznych w kilku zmiennych, popularną alternatywą są kulki Harveya , które są szeroko wykorzystywane przez Consumer Reports . Porównanie w kulkach Harveya (i wykresach radarowych) można znacznie ułatwić poprzez algorytmiczne uporządkowanie zmiennych w celu dodania kolejności.

Doskonałym sposobem wizualizacji struktur w danych wielowymiarowych jest analiza głównych składowych (PCA).

Inną alternatywą jest użycie małych, wbudowanych wykresów słupkowych, które można porównać do wykresów przebiegu w czasie .

Chociaż mapy radarowe i biegunowe są często opisywane jako ten sam typ map, niektóre źródła robią między nimi różnicę, a nawet uważają, że mapa radarowa jest odmianą mapy biegunowej, która nie wyświetla danych w postaci współrzędnych biegunowych.

Zobacz też

Public Domain Artykuł ten zawiera materiały należące do domeny publicznej, pochodzące z Narodowego Instytutu Standardów i Technologii .

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Radar_chart&oldid=1143174416 ”