Rozkład dwumianowy

„Model dwumianowy” przekierowuje tutaj. Aby zapoznać się z modelem dwumianowym w wycenie opcji, zobacz Model wyceny opcji dwumianowych .

Rozkład dwumianowy

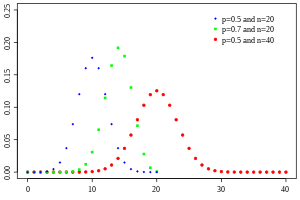
Funkcja masy prawdopodobieństwa
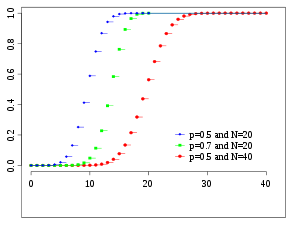
Funkcja dystrybucji skumulowanej
Notacja	${\ Displaystyle B (n, p)}$
Parametry	${\ Displaystyle n \ w \ {0,1,2, \ ldots \}}$ - liczba prób ${\ Displaystyle p \ w [0,1] }$ - prawdopodobieństwo sukcesu dla każdej próby ${\ displaystyle q = 1-p}$
Wsparcie	${\ Displaystyle k \ w \ {0,1, \ ldots, n \}}$ - liczba sukcesów
PMF	${\ Displaystyle {\ binom {n} {k}} p ^ {k} q ^ {nk}}$
CDF	${\ Displaystyle I_ {q} (nk, 1 + k)}$ ( uregulowana niekompletna funkcja beta )
Mieć na myśli	${\ displaystyle np}$
Mediana	${\ Displaystyle \ lfloor np \ rfloor}$ lub ${\ Displaystyle \ lceil np \ rceil}$
Tryb	${\ Displaystyle \ lfloor (n + 1) p \ rfloor}$ lub ${\ Displaystyle \ lceil (n + 1) p \ rceil -1}$
Zmienność	${\ displaystyle npq}$
Skośność	${\ Displaystyle {\ Frac {qp} {\ sqrt {npq}}}}$
Były. kurtoza	${\ Displaystyle {\ Frac {1-6pq} {npq}}}$
Entropia	${\ Displaystyle {\ Frac {1} {2}} \ log _ {2} (2 \ pi enpq) + O \ lewo ({{ \frac {1}{n}}\right)}$ w shannons . W przypadku nat użyj dziennika naturalnego w dzienniku.
MGF	${\ Displaystyle (q + pe ^ {t}) ^ {n}}$
CF	${\ Displaystyle (q + pe ^ {to}) ^ {n}}$
PGF	${\ Displaystyle G (z) = [q + pz] ^ {n}}$
Informacje Fishera	${\ Displaystyle g_ {n} (p) = {\ Frac {n} {pq}}}$ (dla ustalonego ${\ displaystyle n}$ )

Rozkład dwumianowy dla n $trójkącie$ k jak w Pascala Prawdopodobieństwo, że piłka w Galtona z 8 warstwami ( n 8) trafi do centralnego pojemnika ( k = 4) wynosi $}$ Displaystyle

W teorii prawdopodobieństwa i statystyce rozkład dwumianowy z parametrami n i p jest dyskretnym rozkładem prawdopodobieństwa liczby sukcesów w sekwencji n niezależnych eksperymentów , z których każdy zadaje pytanie tak-nie i każdy ma własny wynik o wartości logicznej : sukces (z prawdopodobieństwem p ) lub porażka (z prawdopodobieństwem ${\ displaystyle q = 1-p}$ ). Pojedynczy sukces / porażka jest również nazywany próbą Bernoulliego lub eksperymentem Bernoulliego, a sekwencja wyników nazywana jest procesem Bernoulliego ; dla pojedynczej próby, tj. n = 1, rozkład dwumianowy jest rozkładem Bernoulliego . Rozkład dwumianowy jest podstawą popularnego dwumianowego testu istotności statystycznej .

Rozkład dwumianowy jest często używany do modelowania liczby sukcesów w próbie o rozmiarze n , wylosowanej ze zwracaniem z populacji o rozmiarze N. Jeśli losowanie odbywa się bez zwracania, losowania nie są niezależne, a zatem otrzymany rozkład jest rozkładem hipergeometrycznym , a nie dwumianowym. Jednak dla N znacznie większych niż n rozkład dwumianowy pozostaje dobrym przybliżeniem i jest szeroko stosowany.

Definicje

Prawdopodobieństwo funkcji masowej

Ogólnie, jeśli zmienna losowa X ma rozkład dwumianowy z parametrami i p ∈ [ $0,1$ ], piszemy X ~ B ( n , p . Prawdopodobieństwo uzyskania dokładnie k sukcesów w n niezależnych próbach Bernoulliego wyraża funkcja masy prawdopodobieństwa :

${\ Displaystyle f (k, n, p) =\Pr(k;n,p)=\Pr(X=k)={\binom {n}{k}}p^{k}(1-p)^{nk}}$

dla k = 0, 1, 2, ..., n , gdzie

${\ Displaystyle {\ binom {n} {k}} = {\ Frac {n!} {k! (nk)!}}}$

jest współczynnikiem dwumianowym , stąd nazwa rozkładu. Formułę można rozumieć następująco: k sukcesów występuje z prawdopodobieństwem p ^k i n - k niepowodzeń występuje z prawdopodobieństwem ${\ Displaystyle (1-p) ^ {nk}}$ . Jednak k sukcesów może wystąpić w dowolnym miejscu spośród $prób$ i różne sposoby dystrybucji k w sekwencji n .

Tworząc tabele referencyjne dla prawdopodobieństwa rozkładu dwumianowego, zwykle tabelę wypełnia się do wartości n /2. Dzieje się tak, ponieważ dla k > n /2 prawdopodobieństwo można obliczyć za pomocą jego uzupełnienia jako

${\ Displaystyle f (k, n, p) = f (nk, n, 1-p).}$

Patrząc na wyrażenie f ( k , n , p ) jako funkcję k , istnieje wartość k , która je maksymalizuje. Tę k można znaleźć za pomocą obliczeń

${\ Displaystyle {\ Frac {f (k + 1, n, p)}{f(k,n,p)}}={\frac {(nk)p}{(k+1)(1-p)}}}$

i porównując to z 1. Zawsze istnieje liczba całkowita M , która spełnia

${\ Displaystyle (n + 1) p-1 \ równoważnik M <(n + 1) s.}$

f ( k , n , p ) jest monotonicznie rosnący dla k < M i monotonicznie malejący dla k > M , z wyjątkiem przypadku, gdy ( n + 1) p jest liczbą całkowitą. W tym przypadku istnieją dwie wartości, dla których f jest maksymalne: ( n + 1) p i ( n + 1) p - 1. M jest najbardziej prawdopodobnym wynikiem (czyli najbardziej prawdopodobnym, chociaż nadal może być mało prawdopodobny ogólnie) prób Bernoulliego i nazywa się trybem .

Przykład

Załóżmy, że w rzucie monetą z odchyleniem wypadnie orzeł z prawdopodobieństwem 0,3. Prawdopodobieństwo trafienia dokładnie 4 orłów w 6 rzutach wynosi

${\ Displaystyle f (4,6,0.3) = {\ binom {6} {4}} 0,3 ^ {4} (1-0,3) ^ {6-4} = 0,059535.}$

Dystrybuanta

Skumulowaną funkcję dystrybucji można wyrazić jako:

${\ Displaystyle F (k; n, p) = \ Pr(X\leq k)=\sum _{i=0}^{\lfloor k\rfloor }{n \choose i}p^{i}(1-p)^{ni},}$

gdzie ${\ Displaystyle \ lfloor k \ rfloor}$ jest „piętrem” pod k , tj. największą liczbą całkowitą mniejszą lub równą k .

Można to również przedstawić za pomocą uregulowanej niepełnej funkcji beta w następujący sposób:

${\ Displaystyle {\ rozpocząć {wyrównane} F (k; n, p) & = \ Pr (X \ równoważnik k) \\& = I_ {1-p} (nk, k + 1) \\& = (nk ){n \choose k}\int _{0}^{1-p}t^{nk-1}(1-t)^{k}\,dt.\end{wyrównane}}}$

F jest równoważne skumulowanej funkcji dystrybucji rozkładu :

${\ Displaystyle F (k; n, p) = F _ {F {\ tekst {-dystrybucja}}} \ lewo (x = {\ Frac {1-p} {p}} {\ Frac {k + 1}} nk}};d_{1}=2(nk),d_{2}=2(k+1)\prawo).}$

Poniżej podano niektóre granice postaci zamkniętej dla funkcji dystrybucji skumulowanej .

Nieruchomości

Oczekiwana wartość i wariancja

Jeśli X ~ B ( n , p ), czyli X jest zmienną losową o rozkładzie dwumianowym, gdzie n oznacza całkowitą liczbę eksperymentów, a p prawdopodobieństwo, że każdy eksperyment zakończy się sukcesem, to oczekiwana wartość X wynosi :

${\ Displaystyle \ nazwa operatora {E} [X] = np.}$

Wynika to z liniowości wartości oczekiwanej oraz z faktu, że X jest sumą n identycznych zmiennych losowych Bernoulliego, z których każda ma wartość oczekiwaną p . Innymi słowy, jeśli ${\ Displaystyle X = X_ {1} + \ cdots + X_ {n}}$$)$ Bernoulliego z parametrem p , to i

${\ Displaystyle \ nazwa operatora {E} [X] = \ nazwa operatora {E} [X_ {1} + \ cdots + X_ {n}] = \ nazwa operatora {E} [X_ {1}] + \ cdots + \ nazwa operatora { E} [X_{n}]=p+\cdots +p=np.}$

Wariancja to :

${\ Displaystyle \ nazwa operatora {Var} (X) = npq = np (1-p).}$

Podobnie wynika to z faktu, że wariancja sumy niezależnych zmiennych losowych jest sumą wariancji.

Wyższe chwile

Pierwsze 6 centralnych momentów , zdefiniowanych jako $\ Displaystyle \ mu _ {c} = \ nazwa operatora {E} \ lewo [(X- \ nazwa operatora {E } [X])^{c}\right]}$ , są podane przez

${\ Displaystyle {\ rozpocząć {wyrównane} \ mu _ {1} & = 0, \\\ mu _ {2} & = np (1-p), \\\ mu _ {3} & = np (1- p)(1-2p),\\\mu _{4}&=np(1-p)(1+(3n-6)p(1-p)),\\\mu _{5}&= np(1-p)(1-2p)(1+(10n-12)p(1-p)),\\\mu _{6}&=np(1-p)(1-30p(1- p)(1-4p(1-p))+5np(1-p)(5-26p(1-p))+15n^{2}p^{2}(1-p)^{2}) .\end{wyrównane}}}$

Niecentralne momenty satysfakcjonują

${\ Displaystyle {\ rozpocząć {wyrównane} \ operatorname {E} [X] & = np, \\\nazwaoperatora {E} [X^{2}]&=np(1-p)+n^{2}p^{2},\end{wyrównane}}}$

i na ogół

${\ Displaystyle \ operatorname {E} [X ^ {c}] = \ suma _ {k = 0} ^ {c} \ lewo\{{c \na górze k}\prawo\}n^{\podkreślenie {k}}p^{k},}$

gdzie $\ prawo \}}$ to liczby Stirlinga drugiego rodzaju i $\ cdots (nk + 1)} to$ ) spadająca potęga k $\ displaystyle k}$${\ displaystyle n}$ . Prosta granica następuje przez ograniczenie momentów dwumianowych przez wyższe momenty Poissona :

${\ Displaystyle \ nazwa operatora {E} [X ^ {c}] \ równoważnik \ lewo ({\ Frac {c} {\ log (c / (np) + 1)}} \ prawo) ^ {c} \ równoważnik ( np)^{c}\exp \left({\frac {c^{2}}{2np}}\right).}$

$}$ , że jeśli mi $np$ Displaystyle $\ operatorname {E} [X ^ {c}] {\ Displaystyle c = O ({$ jest co najwyżej stałym czynnikiem oddalonym od ${\ Displaystyle \ nazwa operatora {E} [X] ^ {c}}$

Tryb

Zwykle tryb rozkładu dwumianowego B ( n , p ) jest równy , gdzie ⌊ $\ Displaystyle \ lfloor (n + 1) p \ rfloor}$${\ Displaystyle \ lfloor \ cdot \rfloor}$ to funkcja podłogi . Jednak gdy ( n + 1) p jest liczbą całkowitą, a p nie jest ani 0, ani 1, wówczas rozkład ma dwa tryby: ( n + 1) p i ( n + 1) p - 1. Kiedy p jest równe 0 lub 1, tryb będzie odpowiednio 0 i n . Przypadki te można podsumować w następujący sposób:

${\ Displaystyle {\ tekst {tryb}} = {\ rozpocząć {przypadki} \ lfloor (n + 1) \, p \ rfloor & {\ text{if }}(n+1)p{\text{ to 0 lub liczba niecałkowita}},\\(n+1)\,p\ {\text{ i }}\ (n+1)\,p -1&{\text{if }}(n+1)p\in \{1,\kropki ,n\},\\n&{\text{if }}(n+1)p=n+1.\ zakończyć {przypadki}}}$

Dowód: Niech

${\ Displaystyle f (k) = {\ binom {n} {k}} p ^ {k} q ^ {nk}.}$

p ${\ displaystyle p = 0}$ tylko ${\ displaystyle f (0)}$ ma wartość różną od zera z $displaystyle f (0) = 1}$ . p ${\ Displaystyle p = 1}$ znajdujemy ${\ Displaystyle f (n) = 1}$ i ${\ Displaystyle f (k) = 0$ dla ${ \displaystyle k\neq n}$ . Dowodzi to $n}$ że tryb wynosi 0 dla i $displaystyle$ dla ${\ displaystyle p = 1}$ .

Niech ${\ Displaystyle 0 <p <1}$ . Znaleźliśmy

${\ Displaystyle {\ Frac {f (k + 1)} {f (k)}} = { \frac {(nk)p}{(k+1)(1-p)}}}$ .

Z tego wynika

${\ Displaystyle {\ rozpocząć {wyrównane} k> (n + 1) p-1 \ Strzałka w prawo f (k + 1) <f (k) \\ k=(n+1)p-1\Strzałka w prawo f(k+1)=f(k)\\k<(n+1)p-1\Strzałka w prawo f(k+1)>f(k)\end {wyrównany}}}$

Więc kiedy ${\ Displaystyle (n + 1) p-1}$ jest liczbą całkowitą, to ${\ Displaystyle (n + 1) p-1}$ i ${\ Displaystyle (n + 1) p}$ jest trybem. W przypadku, gdy ${\ Displaystyle (n + 1) p-1 \ notin \ mathbb {Z}}$ , to tylko ${\ Displaystyle \ lfloor (n + 1) p-1 \ rfloor + 1 = \ lfloor (n + 1) p \ rfloor}$ jest trybem.

Mediana

Ogólnie rzecz biorąc, nie ma jednego wzoru na znalezienie mediany dla rozkładu dwumianowego, a nawet może on nie być unikalny. Ustalono jednak kilka wyników specjalnych:

• Jeśli np jest liczbą całkowitą, to średnia, mediana i tryb pokrywają się i są równe np .
• Każda mediana m musi leżeć w przedziale ⌊ np ⌋ ≤ m ≤ ⌈ np ⌉.
• Mediana m nie może leżeć zbyt daleko od średniej: | m − np | ≤ min{ ln 2, max{ p , 1 - p } }.
• Mediana jest unikalna i równa m = round ( np ), gdy | m − np | ≤ min{ p , 1 − p } (z wyjątkiem przypadku, gdy p = 1 / 2 i n jest nieparzyste).
• Kiedy p jest liczbą wymierną (z wyjątkiem p = 1/2 i n nieparzystych), mediana jest niepowtarzalna.
• Gdy p = 1/2 i n 1/2 jest jest 1/2 nieparzyste , dowolna liczba m z przedziału ( n - 1) ≤ m ≤ ( n + 1) medianą rozkładu dwumianowego. Jeśli p = 1/2 i n jest parzyste, to m = n /2 jest jednoznaczną medianą.

Granice ogona

Dla k ≤ np , górne granice można wyprowadzić dla dolnego ogona skumulowanej funkcji dystrybucji ${\ Displaystyle F (k; n, p) = \ Pr (X \leq k)}$ , prawdopodobieństwo, że jest co najwyżej k sukcesów. Pr ${\ Displaystyle \ Pr (X \ geq k) = F (nk; n, 1-p)}$ te granice można również zobaczyć jako granice górnego ogona funkcji dystrybucji skumulowanej dla k ≥ np .

Nierówność Hoeffdinga daje prostą granicę

${\ Displaystyle F (k; n, p) \ równoważnik \ exp \ lewo (-2n \ lewo (p- { \frac {k}{n}}\right)^{2}\right),\!}$

co jednak nie jest zbyt ciasne. W szczególności dla p = 1 mamy to, że F ( k ; n , p ) = 0 (dla ustalonego k , n z k < n ), ale granica Hoeffdinga daje dodatnią stałą.

Ostrzejszą granicę można uzyskać z granicy Chernoffa :

${\ Displaystyle F (k; n, p) \ równoważnik \ exp \ lewo (-nD \ lewo ({\ Frac {k }{n}}\równoległy p\prawo)\prawo)}$

gdzie D ( a || p ) jest względną entropią (lub dywergencją Kullbacka-Leiblera) między monetą a a monetą p (tj. między rozkładem Bernoulliego ( a ) i Bernoulliego ( p )):

${\ Displaystyle D (a \ równoległy p) = (a) \ log {\ Frac {a} {p}} + (1-a) \ log {\ Frac {1-a} {1-p}}. \ !}$

Asymptotycznie ta granica jest dość wąska; zobacz szczegóły.

Można również $ogonie$ granice , koncentracji Można to wykazać, przybliżając współczynnik dwumianu wzorem Stirlinga

${\ Displaystyle F (k; n, p) \ geq {\ frac {1}{\sqrt {8n{\tfrac {k}{n}}(1-{\tfrac {k}{n}})}}}\exp \left(-nD\left({\frac {k }{n}}\równoległy p\prawo)\prawo),}$

co implikuje prostszą, ale luźniejszą granicę

${\ Displaystyle F (k; n, p) \ geq {\ Frac {1} {\ sqrt {2n}}} \ exp \ lewo (-nD \ lewo ({\ Frac {k} {n}} \ równoległy p \prawo)\prawo).}$

Dla p = 1/2 i k ≥ 3 n /8 dla parzystego n można uczynić mianownik stałym:

${\ Displaystyle F (k; n, {\ tfrac {1} {2}}) \ geq {\ Frac {1} {15}} \ exp \ lewo (-16n \ lewo ({\ frac {1} {2} }}-{\frac {k}{n}}\right)^{2}\right).\!}$

Wnioskowanie statystyczne

Szacowanie parametrów

Zobacz także: Rozkład beta § Wnioskowanie bayesowskie

Gdy znane jest n , parametr p można oszacować na podstawie proporcji sukcesów:

${\ Displaystyle {\ widehat {p}} = {\ Frac {x} {n}}.}$

Ten estymator znajduje się za pomocą estymatora największej wiarygodności , a także metody momentów . Ten estymator jest nieobciążony i jednorodny z minimalną wariancją , udowodniony za pomocą twierdzenia Lehmanna-Scheffégo , ponieważ jest oparty na minimalnej statystyce wystarczającej i pełnej (tj.: x ). Jest również spójny zarówno pod względem prawdopodobieństwa, jak i MSE .

Estymator Bayesa w postaci zamkniętej dla p istnieje również w przypadku używania rozkładu Beta jako sprzężonego rozkładu a priori . Używając $,$ jako priori późniejszej

${\ Displaystyle {\ widehat {p}} _ {b} = {\ Frac {x + \ alfa} {n + \ alfa + \ beta}}.}$

Estymator Bayesa jest asymptotycznie wydajny i gdy wielkość próby zbliża się do nieskończoności ( n → ∞), zbliża się do rozwiązania MLE . Estymator Bayesa jest obciążony (ile zależy od a priori), dopuszczalny i spójny w prawdopodobieństwie.

W szczególnym przypadku użycia standardowego rozkładu jednorodnego jako nieinformacyjnego wcześniejszego , ${\ Displaystyle \ nazwa operatora {Beta} (\ alfa = 1, \ beta =1)=U(0,1)}$ , estymator średniej późniejszej przyjmuje postać:

${\ Displaystyle {\ widehat {p}} _ {b} = {\ Frac {x + 1} {n + 2}}.}$

( Tryb późniejszy powinien po prostu prowadzić do estymatora standardowego). Ta metoda nazywa się regułą sukcesji , którą wprowadził w XVIII wieku Pierre-Simon Laplace .

Podczas szacowania p z bardzo rzadkimi zdarzeniami i małym n (np. Jeśli x = 0), użycie standardowego estymatora prowadzi do ${\ displaystyle {\ widehat {p}} = 0,}$ co czasami jest nierealne i niepożądany. W takich przypadkach istnieją różne alternatywne estymatory. Jednym ze sposobów jest użycie estymatora Bayesa, co prowadzi do:

${\ Displaystyle {\ widehat {p}} _ {b} = {\ Frac {1} {n + 2}}.}$

Inną metodą jest wykorzystanie górnej granicy przedziału ufności uzyskanego za pomocą reguły trzech :

${\ Displaystyle {\ widehat {p}} _ {\ tekst {reguła 3}} = {\ Frac {3} {n}}.}$

Przedziały ufności

Główny artykuł: przedział ufności proporcji dwumianowej

Nawet dla dość dużych wartości n rzeczywisty rozkład średniej jest znacząco nienormalny. Z powodu tego problemu zaproponowano kilka metod szacowania przedziałów ufności.

W poniższych równaniach dla przedziałów ufności zmienne mają następujące znaczenie:

• n ₁ to liczba sukcesów z n , całkowita liczba prób
• ${\ Displaystyle {\ widehat {p \}} = {\ Frac {n_ {1}} {n}}}$ to odsetek sukcesów
• ${\ Displaystyle z = 1- {\ tfrac {1} {2}} \ alfa}$ jest kwantylem standardowego rozkładu normalnego (tj. probit ) odpowiadającego docelowemu poziomowi błędów ${\ Displaystyle \alfa}$ . Na przykład dla 95% poziomu ufności błąd ${\ Displaystyle \ alpha}$ = 0,05, więc ${\ Displaystyle 1- {\ tfrac {1} {2}} \ alpha}$ = 0,975 i ${ \displaystyle z}$ = 1,96.

Metoda Walda

Główny artykuł: dwumianowy przedział ufności proporcji § przedział Walda

${\ Displaystyle {\ widehat {p \}} \ pm z {\ sqrt {\ frac {{\ widehat {p \}} (1- {\ widehat {p \}})} {n}}} .}$

Można dodać poprawkę ciągłości 0,5/ n .

Metoda Agrestiego-Coull'a

Główny artykuł: Dwumianowy przedział ufności proporcji § Przedział Agrestiego – Coulla

${\ Displaystyle {\ tylda {p}} \ pm z {\ sqrt {\ Frac {{\ tylda {p}} (1- {\ tylda { p}})}{n+z^{2}}}}}$

Tutaj oszacowanie p jest modyfikowane do

${\ Displaystyle {\ tylda {p}} = {\ Frac {n_ {1} + {\ Frac {1} {2}} z ^ {2}} {n+z^{2}}}}$

Ta metoda działa dobrze dla ${\ displaystyle n> 10}$ i ${\ displaystyle n_ {1} \ neq 0, n}$ . Zobacz tutaj ${\ Displaystyle n \ równoważnik 10}$ . Dla ${\ Displaystyle n_ {1} = 0, n}$ użyj poniższej metody Wilsona (wynik).

Metoda arcsine

Główny artykuł: dwumianowy przedział ufności proporcji § Transformacja arcus sinus

${\ Displaystyle \ sin ^ {2} \ lewo (\ arcsin \ lewo ({\ sqrt {\ widehat {p \}}} \ prawej) \ pm {\ Frac {z} {2 {\ sqrt {n}} }}\Prawidłowy).}$

Metoda Wilsona (punktacja).

Główny artykuł: dwumianowy przedział ufności proporcji § przedział punktacji Wilsona

Oznaczenie w poniższym wzorze różni się od poprzednich wzorów pod dwoma względami:

• Po pierwsze, z _x ma nieco inną interpretację w poniższym wzorze: ma swoje zwykłe znaczenie „ x -tego kwantyla standardowego rozkładu normalnego”, a nie jest skrótem dla „(1 − x )-tego kwantyla”.
• Po drugie, ta formuła nie używa plus-minus do zdefiniowania dwóch granic. Zamiast tego można użyć, $α / 2$$alpha /2}}$ granicę, lub użyć ${$ , aby uzyskać górną granicę. Na przykład: dla poziomu ufności $0,05$ % błąd = , więc dolną granicę uzyskuje się za pomocą ${\ Displaystyle z = z _ {\ alfa / 2} = z_ {0,025} = -1,96}$ , a górną granicę uzyskuje się za pomocą ${\ Displaystyle z = z_ {1- \ alfa / 2} = z_ {0,975}=1,96}$ .

${\ Displaystyle {\ Frac {{\ widehat {p \,}} + {\ Frac { z^{2}}{2n}}+z{\sqrt {{\frac {{\widehat {p\,}}(1-{\widehat {p\,}})}{n}}+{\ frac {z^{2}}{4n^{2}}}}}}{1+{\frac {z^{2}}{n}}}}}$

Porównanie

Tak zwana metoda „dokładna” ( Clopper – Pearsona ) jest najbardziej konserwatywna. ( Dokładne nie oznacza idealnie dokładne; wskazuje raczej, że oszacowania nie będą mniej konserwatywne niż wartość prawdziwa).

Metoda Walda, choć powszechnie zalecana w podręcznikach, jest najbardziej stronnicza.

Powiązane dystrybucje

Sumy dwumianów

Jeśli X ~ B( n , p ) i Y ~ B( m , p ) są niezależnymi zmiennymi dwumianowymi z tym samym prawdopodobieństwem p , to X + Y jest znowu zmienną dwumianową; jego rozkład to Z=X+Y ~ B( n+m , p ):

${\ Displaystyle {\ rozpocząć {wyrównane} \ nazwa operatora {P} (Z = k) & = \ suma _ {i = 0} ^ { k}\left[{\binom {n}{i}}p^{i}(1-p)^{ni}\right]\left[{\binom {m}{ki}}p^{ki} (1-p)^{m-k+i}\right]\\&={\binom {n+m}{k}}p^{k}(1-p)^{n+mk}\end {wyrównany}}}$

Zmienna losowa o rozkładzie dwumianowym X ~ B( n , p ) może być traktowana jako suma n zmiennych losowych o rozkładzie Bernoulliego. Zatem suma dwóch zmiennych losowych o rozkładzie dwumianowym X ~ B( n , p ) i Y ~ B( m , p ) jest równoważna sumie n + m zmiennych losowych o rozkładzie Bernoulliego, co oznacza Z=X+Y ~ B( n+m , p ). Można to również udowodnić bezpośrednio za pomocą reguły dodawania.

Jeśli jednak X i Y nie mają tego samego prawdopodobieństwa p , to wariancja sumy będzie mniejsza niż wariancja zmiennej dwumianowej o rozkładzie ${\ Displaystyle B (n + m, {\ bar {p}}). \,}$

Rozkład dwumianowy Poissona

Rozkład dwumianowy jest szczególnym przypadkiem rozkładu dwumianowego Poissona , który jest rozkładem sumy n niezależnych nieidentycznych prób Bernoulliego B( pi ₎ .

Stosunek dwóch rozkładów dwumianowych

Wynik ten został po raz pierwszy uzyskany przez Katza i współautorów w 1978 roku.

Niech X ~ B( n , p ₁ ) i Y ~ B( m , p ₂ ) będą niezależne. Niech T = ( X / n )/( Y / m ).

Wówczas log( T ) ma w przybliżeniu rozkład normalny ze średnią log( p ₁ / p ₂ ) i wariancją ((1/ p ₁ ) − 1)/ n + ((1/ p ₂ ) − 1)/ m .

Dwumiany warunkowe

Jeśli X ~ B( n , p ) i Y | X ~ B( X , q ) (rozkład warunkowy Y , dany X ), wtedy Y jest prostą dwumianową zmienną losową o rozkładzie Y ~ B( n , pq ).

Na przykład wyobraź sobie, że rzucasz n piłek do kosza U _X i zabierasz piłki, które trafiły, i rzucasz je do innego kosza U _Y . Jeśli p to prawdopodobieństwo trafienia U _{X ,} to X ~ B( n , p ) to liczba piłek, które trafią U _X . Jeśli q jest prawdopodobieństwem trafienia U _Y , to liczba piłek, które trafiły U _{Y ,} wynosi Y ~ B( X , q ), a zatem Y ~ B ( n , pq ).

[Dowód]

Ponieważ ${\ Displaystyle X \ sim B (n, p)}$ i ${\ Displaystyle Y \ sim B (X, q)}$ , zgodnie z prawem całkowitego prawdopodobieństwo ,

${\ Displaystyle {\ rozpocząć {wyrównane} \ Pr [Y = m] & = \ suma _ {k = m} ^ {n} \ Pr [Y = m \ mid X=k]\Pr[X=k]\\[2pt]&=\sum _{k=m}^{n}{\binom {n}{k}}{\binom {k}{m}} p^{k}q^{m}(1-p)^{nk}(1-q)^{km}\end{wyrównane}}}$

ponieważ ${\ Displaystyle {\ tbinom {n} {k}}} {\ tbinom {k} {m}} = {\ tbinom {n}{m}}{\tbinom {nm}{km}},}$ powyższe równanie można zapisać jako

${\ Displaystyle \ Pr [ Y=m]=\sum _{k=m}^{n}{\binom {n}{m}}{\binom {nm}{km}}p^{k}q^{m}(1- p)^{nk}(1-q)^{km}}$

${\ Displaystyle p ^ {k} = p ^ {m} p ^ {km}}$ i wyciąganie wszystkich terminów, które nie zależą od k $\ displaystyle k}$ z suma teraz daje

${\ Displaystyle {\ zacząć {wyrównane}\Pr[Y=m]&={\binom {n}{m}}p^{m}q^{m}\left(\sum _{k=m}^{n}{\binom {nm}{km}}p^{km}(1-p)^{nk}(1-q)^{km}\right)\\[2pt]&={\binom {n}{m}} (pq)^{m}\left(\suma _{k=m}^{n}{\binom {nm}{km}}\left(p(1-q)\right)^{km}(1 -p)^{nk}\right)\end{wyrównane}}}$

Po podstawieniu w powyższym wyrażeniu otrzymujemy ${\ displaystyle i = km}$

${\ Displaystyle \Pr[Y=m]={\binom {n}{m}}(pq)^{m}\left(\sum _{i=0}^{nm}{\binom {nm}{i}} (p-pq)^{i}(1-p)^{nmi}\prawo)}$

Zauważ, że suma (w nawiasach) powyżej jest równa ${\ Displaystyle (p-pq + 1-p) ^ {nm}}$ przez twierdzenie dwumianowe . Zastąpienie tego w końcu daje

${\ styl wyświetlania {\begin{wyrównane}\Pr[Y=m]&={\binom {n}{m}}(pq)^{m}(p-pq+1-p)^{nm}\\[4pt ]&={\binom {n}{m}}(pq)^{m}(1-pq)^{nm}\end{wyrównane}}}$

a zatem ${\ Displaystyle Y \ sim B (n, pq)}$ zgodnie z życzeniem.

Rozkład Bernoulliego

Rozkład Bernoulliego jest szczególnym przypadkiem rozkładu dwumianowego, gdzie n = 1. Symbolicznie X ~ B(1, p ) ma takie samo znaczenie jak X ~ Bernoulli( p ). I odwrotnie, każdy rozkład dwumianowy B( n , p ) jest rozkładem sumy n niezależnych prób Bernoulliego , Bernoulliego( p ), z których każda ma to samo prawdopodobieństwo p .

Normalne przybliżenie

Zobacz także: Dwumianowy przedział ufności proporcji § Normalny przedział aproksymacji

Dwumianowa funkcja masy prawdopodobieństwa i aproksymacja normalnej funkcji gęstości prawdopodobieństwa dla n = 6 i p = 0,5

Jeśli n jest wystarczająco duże, to skośność rozkładu nie jest zbyt duża. W tym przypadku rozsądne przybliżenie B( n , p ) daje rozkład normalny

${\ Displaystyle {\ mathcal {N}} (np, \, np (1-p)),}$

a to podstawowe przybliżenie można w prosty sposób poprawić, stosując odpowiednią poprawkę na ciągłość . Podstawowe przybliżenie ogólnie poprawia się wraz ze n (co najmniej 20) i jest lepsze, gdy p nie jest bliskie 0 lub 1. Można zastosować różne praktyczne zasady , aby zdecydować, czy n jest wystarczająco duże, a p jest wystarczająco daleko od skrajności zero lub jeden:

• Jedna zasada mówi, że dla n > 5 normalne przybliżenie jest odpowiednie, jeśli bezwzględna wartość skośności jest ściśle mniejsza niż 0,3; to znaczy, jeśli

${\ Displaystyle {\ Frac {| 1-2 p |} {\ sqrt {np (1-p)}}} = {\ Frac {1} {\ sqrt {n}}} \ lewo | {\ sqrt {\ frac {1-p}{p}}}-{\sqrt {\frac {p}{1-p}}}\,\right|<0.3.}$

Można to sprecyzować za pomocą twierdzenia Berry'ego – Esseena .

• Silniejsza reguła mówi, że przybliżenie normalne jest właściwe tylko wtedy, gdy wszystko w zakresie 3 odchyleń standardowych od jego średniej mieści się w zakresie możliwych wartości; to znaczy tylko wtedy, gdy

${\ Displaystyle \ mu \ pm 3 \ sigma = np \ pm 3 {\ sqrt {np (1-p)}} \ in (0, n).} Ta reguła odchylenia standardowego 3 jest równoważna następującym warunkom$

: co implikuje również pierwszą regułę powyżej.

${\ Displaystyle n> 9 \ lewo ({\ Frac {1-p} {p}} \ prawo) \ quad {\ tekst {i}} \ quad n> 9 \ lewo ({\ frac {p} {1- p}}\prawo).}$

[Dowód]

n ${\ Displaystyle np \ pm 3 {\ sqrt {np (1-p)}} \ in (0, n)}$ całkowicie równoważne żądaniu To

${\ Displaystyle np-3 {\ sqrt {np (1-p)}}> 0 \ quad {\ tekst {i}} \ quad np + 3 {\ sqrt {np (1-p)} <n.}$

Przesuwanie terminów wokół plonów:

${\ Displaystyle np> 3 {\ sqrt {np (1-p)}} \ quad {\ tekst {i}} \ quad n (1-p)> 3 {\ sqrt {np (1-p)}}. }$

Ponieważ możemy zastosować potęgę do kwadratu i podzielić przez odpowiednie czynniki $displaystyle n(1-p)^{2}}$$p$$displaystyle np ^ {2}$ ( , aby otrzymać żądane warunki:

${\ Displaystyle n> 9 \ lewo ({\ Frac {1-p} {p}} \ prawo) \ quad {\ tekst {i}} \ quad n> 9 \ lewo ({\ frac {p} {1- p}}\prawo).}$

Zauważ, że te warunki automatycznie implikują, że ${\ displaystyle n> 9}$ . Z drugiej strony zastosuj ponownie pierwiastek kwadratowy i podziel przez 3,

${\ Displaystyle {\ Frac {\ sqrt {n}} {3}}> {\ sqrt {\ Frac {1-p} {p }}}>0\quad {\text{i}}\quad {\frac {\sqrt {n}}{3}}>{\sqrt {\frac {p}{1-p}}}>0. }$

Odejmując drugi zbiór nierówności od pierwszego otrzymujemy:

${\ Displaystyle {\ Frac {\ sqrt {n}}} {3}}> {\ sqrt {\ Frac {1-p} {p}}} - {\ sqrt {\ frac {p} {1-p}} }>-{\frac {\sqrt {n}}{3}};}$

a więc pożądana pierwsza reguła jest spełniona,

${\ Displaystyle \ lewo | {\ sqrt {\ Frac {1-p} {p}}} - {\ sqrt {\ Frac {p} {1-p}}} \, \ prawo | <{\ frac {\ sqrt {n}}{3}}.}$

• Inną powszechnie stosowaną zasadą jest to, że obie wartości i $\$$displaystyle n (1-p)}$ muszą być większe lub równe 5. Jednak konkretna liczba różni się w zależności źródła i zależy od tego, jak dobrego przybliżenia ktoś chce. W szczególności, jeśli użyje się 9 zamiast 5, reguła implikuje wyniki podane w poprzednich akapitach.

[Dowód]

$,$ że obie wartości i $\ Displaystyle n ($$p)}$ większe niż 9. łatwo mieć to

${\ Displaystyle np \ geq 9> 9 (1-p) \ quad {\ tekst {i}} \ quad n (1-p) \ geq 9> 9 p.}$

Musimy teraz tylko podzielić przez odpowiednie czynniki $\ displaystyle p$ , aby $}$ alternatywną postać reguły 3 odchyleń standardowych:

${\ Displaystyle n> 9 \ lewo ({\ Frac {1-p} {p}} \ prawo) \ quad {\ tekst {i}} \ quad n> 9 \ lewo ({\ frac {p} {1- p}}\prawo).}$

Poniżej przedstawiono przykład zastosowania korekty ciągłości . Załóżmy, że ktoś chce obliczyć Pr( X ≤ 8) dla dwumianowej zmiennej losowej X . Jeśli Y ma rozkład określony przez przybliżenie normalne, to Pr( X ≤ 8) jest przybliżone przez Pr ( Y ≤ 8,5). Dodanie 0,5 to poprawka na ciągłość; nieskorygowane przybliżenie normalne daje znacznie mniej dokładne wyniki.

To przybliżenie, znane jako twierdzenie de Moivre'a-Laplace'a , pozwala zaoszczędzić czas przy ręcznym wykonywaniu obliczeń (dokładne obliczenia z dużymi n są bardzo uciążliwe); historycznie było to pierwsze użycie rozkładu normalnego, wprowadzone w książce Abrahama de Moivre The Doctrine of Chances w 1738 r. Obecnie można to postrzegać jako konsekwencję centralnego twierdzenia granicznego , ponieważ B( n , p ) jest suma n niezależnych zmiennych Bernoulliego o identycznym rozkładzie z parametrem p . Fakt ten jest podstawą testu hipotezy , „testu proporcjonalnego z”, dla wartości p przy użyciu x/n , proporcji próby i estymatora p , we wspólnej statystyce testowej .

Załóżmy na przykład, że losujemy n osób z dużej populacji i pytamy ich, czy zgadzają się z pewnym stwierdzeniem. Odsetek osób, które się zgodzą, będzie oczywiście zależał od próby. Gdyby grupy n osób były pobierane wielokrotnie i naprawdę losowo, proporcje odpowiadałyby przybliżonemu rozkładowi normalnemu ze średnią równą rzeczywistej proporcji p zgodności w populacji i odchyleniem standardowym

${\ Displaystyle \ sigma = {\ sqrt {\ Frac {p (1-p)} {n}}}}$

Przybliżenie Poissona

Rozkład dwumianowy zbiega się w kierunku rozkładu Poissona , gdy liczba prób dąży do nieskończoności, podczas gdy iloczyn np zbiega się do skończonej granicy. Dlatego rozkład Poissona z parametrem λ = np może być użyty jako przybliżenie B( n , p ) rozkładu dwumianowego, jeśli n jest wystarczająco duże, a p jest wystarczająco małe. Zgodnie z dwiema praktycznymi regułami przybliżenie to jest dobre, jeśli n ≥ 20 i p ≤ 0,05 lub jeśli n ≥ 100 i np ≤ 10.

Na temat dokładności przybliżenia Poissona zob. Novak, rozdz. 4 i odniesienia w nim zawarte.

Dystrybucje ograniczające

• Twierdzenie o granicy Poissona : Gdy n zbliża się do ∞, a p dąży do 0 przy ustalonym produkcie np , rozkład dwumianowy ( n , p ) zbliża się do rozkładu Poissona z wartością oczekiwaną λ = np .
• Twierdzenie de Moivre'a – Laplace'a : Gdy n zbliża się do ∞, podczas gdy p pozostaje stałe, rozkład

${\ Displaystyle {\ Frac {X-np} {\ sqrt {np (1-p)}}}}$

zbliża się do rozkładu normalnego z wartością oczekiwaną 0 i wariancją 1. Ten wynik jest czasami luźno powiedziane, mówiąc, że rozkład X jest asymptotycznie normalny z wartością oczekiwaną 0 i wariancją 1. Wynik ten jest szczególnym przypadkiem centralnego twierdzenia granicznego .

Dystrybucja beta

Rozkład dwumianowy i rozkład beta to różne widoki tego samego modelu powtarzanych prób Bernoulliego. Rozkład dwumianowy to PMF k sukcesów przy n niezależnych zdarzeniach, z których każde ma prawdopodobieństwo p sukcesu. Matematycznie, gdy α = k + 1 i β = n - k + 1 , rozkład beta i rozkład dwumianowy są powiązane współczynnikiem n + 1 :

${\ Displaystyle \ nazwa operatora {Beta} (p; \ alfa; \ beta) = (n + 1) B (k; n;p)}$

Rozkłady beta zapewniają również rodzinę wcześniejszych rozkładów prawdopodobieństwa dla rozkładów dwumianowych we wnioskowaniu bayesowskim :

${\ Displaystyle P (p; \ alfa, \ beta) = {\ Frac {p ^ {\ alfa -1} (1-p) ^ {\ beta -1}} {\ nazwa operatora {Beta} (\ alfa, \ beta )}}.}$

Biorąc pod uwagę jednolity a priori, rozkład późniejszy prawdopodobieństwa sukcesu p przy n niezależnych zdarzeniach z k obserwowanymi sukcesami jest rozkładem beta.

Generowanie liczb losowych

Dalsze informacje: Próbkowanie liczb pseudolosowych

0 Metody generowania liczb losowych , w których rozkład krańcowy jest rozkładem dwumianowym, są dobrze ugruntowane. Jednym ze sposobów generowania losowych próbek zmiennych z rozkładu dwumianowego jest użycie algorytmu inwersji. Aby to zrobić, należy obliczyć prawdopodobieństwo, że Pr( X = k ) dla wszystkich wartości k od do n . (Prawdopodobieństwa te powinny sumować się do wartości bliskiej jedności, aby objąć całą przestrzeń próbki). Następnie, używając generatora liczb pseudolosowych do generowania próbek równomiernie między 0 a 1, można przekształcić obliczone próbki w liczby dyskretne za pomocą prawdopodobieństwa obliczone w pierwszym kroku.

Historia

Ten rozkład został wyprowadzony przez Jacoba Bernoulliego . Rozważył przypadek, w którym p = r /( r + s ), gdzie p jest prawdopodobieństwem sukcesu, a r i s są dodatnimi liczbami całkowitymi. Blaise Pascal rozważał wcześniej przypadek, w którym p = 1/2.

Zobacz też

• Regresja logistyczna
• Rozkład wielomianowy
• Ujemny rozkład dwumianowy
• Rozkład beta-dwumianowy
• Miara dwumianowa, przykład miary multifraktalnej .
• Mechanika statystyczna
• Lemat o stosach , wynikowe prawdopodobieństwo, gdy XOR -uje ​​niezależne zmienne boolowskie

Dalsza lektura

• Hirsch, Werner Z. (1957). „Rozkład dwumianowy - sukces lub porażka, jakie jest prawdopodobieństwo?” . Wprowadzenie do współczesnej statystyki . Nowy Jork: MacMillan. s. 140–153.
•   Neter, Jan; Wasserman, William; Whitmore, GA (1988). Statystyka stosowana (wyd. Trzecie). Boston: Allyn & Bacon. s. 185–192. ISBN 0-205-10328-6 .

Linki zewnętrzne

• Grafika interaktywna: Relacje dystrybucji jednowymiarowej
• Kalkulator formuły rozkładu dwumianowego
• Różnica dwóch zmiennych dwumianowych: XY lub |XY|
• Zapytanie o dwumianowy rozkład prawdopodobieństwa w WolframAlpha