Rozkład t - Studenta

t -Studenta . Aby zapoznać się z zastosowaniami w statystyce, zobacz Test t-Studenta .

Student t

Funkcja gęstości prawdopodobieństwa
Funkcja dystrybucji skumulowanej
Parametry	${\ Displaystyle \ nu > 0}$ stopnie swobody ( rzeczywiste )
Wsparcie	${\ Displaystyle x \ w (- \ infty, \ infty)}$
PDF	${\ Displaystyle \ textstyle {\ Frac {\ Gamma \ lewo ({\ Frac {\ nu + 1} 2}}\right)}{{\sqrt {\nu \pi }}\,\Gamma \left({\frac {\nu }{2}}\right)}}\left(1+{\frac { x^{2}}{\nu }}\right)^{-{\frac {\nu +1}{2}}}\!}$
CDF	${\ Displaystyle {\ rozpocząć {matrix} {\ Frac {1} {2}} + x \ Gamma \ lewo ({\ Frac {\ nu + 1} {2}} \ prawo) \ razy \\ [0,5 em] {\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2} }};-{\frac {x^{2}}{\nu }}\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\frac {\nu }{2 }}\right)}}\end{macierz}}}$ gdzie 2 F 1 jest funkcją hipergeometryczną
Mieć na myśli	0 dla ${\ displaystyle \ nu > 1}$ , poza tym nieokreślony
Tryb	0
mediany	0
Zmienność	${\ Displaystyle \ textstyle {\ Frac {\ nu} {\ nu -2}}}$ dla ${\ Displaystyle \ nu > 2}$ ∞ dla ${\ Displaystyle 1 <\ nu \leq 2}$ , inaczej niezdefiniowany
Skośność	0 for $\nu >3$, otherwise undefined
Były. kurtoza	${\ Displaystyle \ textstyle {\ Frac {6} {\ nu -4}}}$ dla ${\ Displaystyle \ nu > 4}$ , ∞ dla ${\ Displaystyle 2 <\ nu \leq 4}$ , inaczej niezdefiniowany
Entropia	${\ Displaystyle {\ rozpocząć {matrix} {\ Frac {\ nu + 1} {2}} \ lewo [\ psi \ lewo ({\ Frac {1 + \ nu} {2}} \ prawej) - \ psi \ left({\frac {\nu }{2}}\right)\right]\\[0.5em]+\ln {\left[{\sqrt {\nu }}B\left({\frac {\nu }{2}},{\frac {1}{2}}\right)\right]}\,{\scriptstyle {\text{(nats)}}}\end{macierz}}}$ ψ: funkcja digamma , B : funkcja beta
MGF	nieokreślony
CF	${\ Displaystyle \ textstyle {\ Frac {K _ {\ nu / 2} \ lewo ({\sqrt {\nu }}|t|\right)\cdot \left({\sqrt {\nu }}|t|\right)^{\nu /2}}{\Gamma (\nu /2 ) 2 ^ {\ nu / 2-1}}}}$ dla ${\ Displaystyle \ nu > 0}$ ${\ Displaystyle K _ {\ nu} (x)}$ : zmodyfikowana funkcja Bessela drugiego rodzaju

W prawdopodobieństwie i statystyce rozkład t - Studenta (lub po prostu rozkład t rozkładów ) to dowolny członek rodziny ciągłych prawdopodobieństwa , które powstają podczas szacowania średniej populacji o rozkładzie normalnym w sytuacjach, gdy wielkość próby jest mała, a standard populacji odchylenie nie jest znane. Został opracowany przez angielskiego statystyka Williama Sealy'ego Gosseta pod pseudonimem „Student”.

Rozkład t odgrywa rolę w wielu szeroko stosowanych analizach statystycznych, w tym w teście t - Studenta do oceny istotności statystycznej różnicy między dwiema średnimi z próby, konstrukcji przedziałów ufności dla różnicy między dwiema średnimi z populacji oraz w liniowym analiza regresji . Rozkład t- Studenta pojawia się również w analizie bayesowskiej danych z rodziny normalnej.

Jeśli weźmiemy próbkę obserwacji z rozkładu normalnego, wówczas $rozkład$ t z stopniami swobody można zdefiniować jako rozkład $}$ położenie średniej próbki względem średniej prawdziwej, podzielonej przez odchylenie standardowe próbki, po pomnożeniu przez termin standaryzujący ${\ displaystyle {\ sqrt {n}}}$ . W ten sposób t można wykorzystać do skonstruowania przedziału ufności dla prawdziwej średniej.

Rozkład t jest symetryczny i ma kształt dzwonu, podobnie jak rozkład normalny. Jednak t ma cięższe ogony, co oznacza, że ​​jest bardziej podatny na generowanie wartości, które są dalekie od jego średniej. To sprawia, że ​​jest to przydatne do zrozumienia zachowania statystycznego niektórych typów stosunków wielkości losowych, w których zmienność mianownika jest wzmacniana i może dawać wartości odstające, gdy mianownik stosunku zbliża się do zera. Szczególnym przypadkiem uogólnionego rozkładu hiperbolicznego jest rozkład t- Studenta .

Historia i etymologia

Statystyk William Sealy Gosset, znany jako „Student”

W statystyce rozkład t został po raz pierwszy wyprowadzony jako rozkład a posteriori w 1876 roku przez Helmerta i Lürotha . Rozkład t pojawił się również w bardziej ogólnej formie jako rozkład typu IV Pearsona w artykule Karla Pearsona z 1895 roku.

W literaturze anglojęzycznej nazwa dystrybucji pochodzi od artykułu Williama Sealy'ego Gosseta z 1908 r. W Biometrika pod pseudonimem „Student”. Jedna wersja pochodzenia pseudonimu jest taka, że ​​​​pracodawca Gosseta wolał, aby pracownicy używali pseudonimów podczas publikowania artykułów naukowych zamiast ich prawdziwego nazwiska, więc użył nazwiska „Student”, aby ukryć swoją tożsamość. Inna wersja mówi, że Guinness nie chciał, aby ich konkurenci wiedzieli, że używają testu t do określenia jakości surowca.

Gosset pracował w Guinness Brewery w Dublinie w Irlandii i interesował się problemami małych próbek - na przykład właściwościami chemicznymi jęczmienia, w przypadku których rozmiary próbek mogą wynosić zaledwie 3. Artykuł Gosseta odnosi się do rozkładu jako „rozkład częstotliwości odchyleń standardowych próbek pobranych z normalnej populacji”. Stało się dobrze znane dzięki pracy Ronalda Fishera , który nazwał rozkład „rozkładem Studenta” i przedstawił wartość testową literą t .

Jak rozkład Studenta wynika z próbkowania

Niech ${\ textstyle X_ {1}, \ ldots, X_ {n}}$ będzie niezależnie i identycznie wylosowany z rozkładu ${\ Displaystyle {\ mathcal {N}} ( \ mu , \ sigma ^ {2})}$ , tj. jest to próbka o rozmiarze $sigma$ populacji o rozkładzie normalnym z oczekiwaną wartością średnią $i$ σ $^{2}}$$\ displaystyle \$ .

Pozwalać

${\ Displaystyle {\ bar {X}} = {\ Frac {1} {n}} \ suma _ {i = 1} ^ {n} X_ {i}}$

być próbką średnią i niech

${\ Displaystyle S ^ {2} = {\ Frac {1} {n-1}} \ suma _ {i = 1} ^ {n}(X_{i}-{\bar {X}})^{2}}$

będzie wariancją próbki ( skorygowaną Bessela ). Następnie zmienna losowa

${\ Displaystyle {\ Frac {{\ bar {X}} - \ mu} {\ sigma / {\ sqrt {n}}}}}$

ma standardowy rozkład normalny (tzn. normalny ze średnią oczekiwaną 0 i wariancją 1) oraz zmienną losową

${\ Displaystyle {\ Frac {{\ bar {X}} - \ mu} {S / {\ sqrt {n}}}}}$

tj $za$ gdzie zostało podstawione $swobody$$-$ rozkład t Studenta ze Ponieważ jedyną nieobserwowalną wielkością w tym wyrażeniu jest μ $\$$można$$mu,},$ wykorzystać do wyznaczenia przedziałów ${\textstyle \mu.}$ Licznik i mianownik w powyższym wyrażeniu są statystycznie niezależnymi zmiennymi losowymi, mimo że są oparte na tej samej próbie ${\textstyle X_ {1}, \ ldots , X_ {n} }$ . Można to zobaczyć obserwując, że ${\ textstyle \ operatorname {cov} ({\ overline {X}}, \, X_ {i} - {\ overline {X }})=0,}$$są liniowymi$$,$ że obie samego zestawu zmienne losowe.

Definicja

Funkcja gęstości prawdopodobieństwa

Rozkład t - Studenta ma funkcję gęstości prawdopodobieństwa (PDF) określoną przez

${\ Displaystyle f (t) = {\ Frac {\ Gamma ( {\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+ {\frac {t^{2}}{\nu}}\right)^{-(\nu +1)/2},}$

gdzie jest $swobody$ stopni i $_$ funkcją gamma . Można to również zapisać jako

${\ Displaystyle f (t) = {\ Frac {1} {{\ sqrt { \nu }}\,\mathrm {B} ({\frac {1}{2}},{\frac {\nu }{2}})}}\left(1+{\frac {t^{2 }}{\nu }}\right)^{-(\nu +1)/2},}$

gdzie B jest funkcją Beta . W szczególności dla stopni swobody o wartościach całkowitych mamy: ${\ displaystyle \ nu}$

Nawet dla ${\ displaystyle \ nu > 1}$

${\ Displaystyle {\ Frac {\ Gamma ({\ Frac {\ nu + 1} {2}})} {{\ sqrt {\ nu \ pi}} \, \ Gamma ({\ Frac {\ nu}} {2 }})}}={\frac {(\nu -1)(\nu -3)\cdots 5\cdot 3}{2{\sqrt {\nu }}(\nu -2)(\nu -4 )\cdots 4\cdot 2\,}}\cdot }$

dla nieparzystego, ${\ displaystyle \ nu > 1}$

${\ Displaystyle {\ Frac {\ Gamma ({\ Frac {\ nu + 1} {2}})} {{\ sqrt {\ nu \ pi}} \ \ Gamma ({\ Frac {\ nu}} {2 }})}}={\frac {(\nu -1)(\nu -3)\cdots 4\cdot 2}{\pi {\sqrt {\nu }}(\nu -2)(\nu - 4)\cdots 5\cdot 3\,}}\cdot \!}$

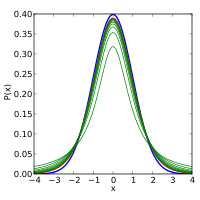
Funkcja gęstości prawdopodobieństwa jest symetryczna , a jej ogólny kształt przypomina kształt dzwonu zmiennej o rozkładzie normalnym ze średnią 0 i wariancją 1, z tym wyjątkiem, że jest nieco niższa i szersza. Wraz ze wzrostem liczby stopni swobody $jest$ t zbliża się do rozkładu normalnego ze średnią 0 i wariancją 1. Z tego powodu również znany jako parametr normalności.

Poniższe obrazy pokazują gęstość rozkładu t dla rosnących wartości ${\ displaystyle \ nu}$ . Rozkład normalny jest pokazany jako niebieska linia dla porównania. $,$ że rozkład t (czerwona linia) zbliża się do rozkładu normalnego wraz ze wzrostem.

Gęstość rozkładu t (kolor czerwony) dla 1, 2, 3, 5, 10 i 30 stopni swobody w porównaniu ze standardowym rozkładem normalnym (kolor niebieski). Poprzednie działki zaznaczone na zielono.

1 stopień swobody

2 stopnie swobody

3 stopnie swobody

5 stopni swobody

10 stopni swobody

30 stopni swobody

Dystrybuanta

Funkcję dystrybucji skumulowanej (CDF) można zapisać w kategoriach I , uregulowanej niepełnej funkcji beta . dla t > 0,

${\ Displaystyle F (t) = \ int _ {- \ infty} ^ {t}f(u)\,du=1-{\tfrac {1}{2}}I_{x(t)}\left({\tfrac {\nu }{2}},{\tfrac {1 }{2}}\prawo),}$

Gdzie

${\ Displaystyle x (t) = {\ Frac {\ nu} {t ^ {2} + \ nu}}.}$

Inne wartości można by uzyskać przez symetrię. Alternatywna formuła, ważna dla , to ${\ displaystyle t ^ {2}<\ nu$ }

$\ Displaystyle \ int _ {- \ infty} ^ {t} f (u) \, du = {\ tfrac {1} {2}} + t {\ Frac {\ Gamma \ lewo ({\ tfrac {1}{2}}(\nu +1)\right)}{{\sqrt {\pi \nu }}\,\Gamma \left({\tfrac {\nu }{2}}\right)} }\,{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}}(\nu +1);{\tfrac {3} {2}};-{\tfrac {t^{2}}{\nu }}\right),}$

gdzie ₂ F ₁ jest szczególnym przypadkiem funkcji hipergeometrycznej .

Aby uzyskać informacje na temat jego odwrotnej funkcji dystrybucji skumulowanej, zobacz funkcja kwantylowa § Rozkład t-Studenta .

Przypadki specjalne

$postać$ wartości dają prostą rozkładu t Studenta.

${\ displaystyle \ nu}$	PDF	CDF	notatki
1	${\ Displaystyle {\ Frac {1} {\ pi (1 + t ^ {2})}}}$	${\ Displaystyle {\ Frac {1} {2}} + {\ Frac {1} {\ pi}} \ arctan (t)}$	Zobacz rozkład Cauchy'ego
2	${\ Displaystyle {\ Frac {1} {2 {\ sqrt {2}} \ lewo (1 + {\ Frac {t ^ {2}} {2}} \right)^{3/2}}}}$	${\ Displaystyle {\ Frac {1} {2}} + {\ Frac {t} {2 {\ sqrt {2}} {\ sqrt {1 + {\ Frac { t^{2}}{2}}}}}}}$
3	${\ Displaystyle {\ Frac {2} {\ pi {\ sqrt {3}} \ lewo (1 + {\ Frac {t ^ {2}} {3}} \ dobrze)^{2}}}}$	${\ Displaystyle {\ Frac {1} {2}} + {\ Frac {1} {\ pi}} {\ lewo [{\frac {1}{\sqrt {3}}}{\frac {t}{1+{\frac {t^{2}}{3}}}}+\arctan \left({\frac { t}{\sqrt {3}}}\prawo)\prawo]}}$
4	${\ Displaystyle {\ Frac {3} {8 \ lewo (1 + {\ Frac {t ^ {2}} {4}} \ prawej) ^ {5/2 }}}}$	${\ Displaystyle {\ Frac {1} {2}} + {\ Frac {3} {8}} {\ frac {t}{\sqrt {1+{\frac {t^{2}}{4}}}}}{\left[1-{\frac {1}{12}}{\frac {t^{ 2}}{1+{\frac {t^{2}}{4}}}}\right]}}$
5	${\ Displaystyle {\ Frac {8} {3 \ pi {\ sqrt {5}} \ lewo (1 + {\ Frac {t ^ {2}} {5} }\prawo)^{3}}}}$	${\ Displaystyle {\ Frac {1} {2}} + {\ Frac {1} {\ pi}} {\ lewo [{\ Frac {t} {{\ sqrt {5}} \ lewo (1+ {\ frac {t^{2}}{5}}\right)}}\left(1+{\frac {2}{3\left(1+{\frac {t^{2}}{5}}\ prawo)}}\right)+\arctan \left({\frac {t}{\sqrt {5}}}\right)\right]}}$
${\ Displaystyle \ infty}$	${\ Displaystyle {\ Frac {1} {\ sqrt {2 \ pi}}} e ^ {- t ^ {2}/2}}$	${\ Displaystyle {\ Frac {1} {2}} {\ lewo [1 + \ operatorname {erf} \ lewo ({\ Frac {t}} {\ sqrt {2 }}}\prawo)\prawo]}}$	Zobacz Rozkład normalny , Funkcja błędu

Jak powstaje rozkład t

Dystrybucja próbek

Niech ${\ Displaystyle x_ {1}, \ ldots, x_ {n}}$ będą liczbami obserwowanymi w próbce z populacji o ciągłym rozkładzie o wartości oczekiwanej ${\ displaystyle \ mu}$ . Średnia próbki i wariancja próbki są podane przez:

${\ Displaystyle {\ rozpocząć {wyrównane} {\ bar {x}} & = {\ Frac {x_ {1} + \ cdots + x_ {n}} {n}}, \\ [5pt] s ^ {2} &={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}.\end{wyrównane} }}$

Wynikowa wartość t wynosi

${\ Displaystyle t = {\ Frac {{\ bar {x}} - \ mu} {s / {\ sqrt {n}}}}.}$

Rozkład t ze $t,$ swobody to rozkład próbkowania wartości gdy próbki składają się z obserwacji o identycznym rozkładzie z populacji o rozkładzie normalnym Zatem dla celów wnioskowania t jest użyteczną „ wielkością kluczową ” w przypadku, gdy średnia i wariancja ${\ Displaystyle (\ mu, \ sigma ^ {2})}$$\sigma ^{2}}$ nieznanymi parametrami populacji w tym sensie, że wartość t ma wtedy rozkład prawdopodobieństwa, który nie zależy ani od $displaystyle$${\$ .

Wnioskowanie bayesowskie

Główny artykuł: wnioskowanie bayesowskie

W statystyce bayesowskiej (skalowany, przesunięty) rozkład t powstaje jako rozkład krańcowy nieznanej średniej rozkładu normalnego, gdy zależność od nieznanej wariancji została zmarginalizowana:

${\ Displaystyle {\ rozpocząć {wyrównane} p (\ mu \ mid D, I) = & \ int p (\ mu, \ sigma ^ {2} \ mid D, I) \, d \ sigma ^ {2} \ \=&\int p(\mu \mid D,\sigma ^{2},I)\,p(\sigma ^{2}\mid D,I)\,d\sigma ^{2},\end {wyrównany}}}$

gdzie $oznacza$ dane i reprezentuje wszelkie inne $,$$.$ mogły zostać Rozkład jest zatem $}$ rozkładu warunkowego danych danych i $Displaystyle$ rozkładem krańcowym $}$$\ sigma ^ {2}$ dane.

Z $danych$ , jeśli są nieinformacyjne lub płaskie, lokalizacja przed ${\ displaystyle p (\ mu \ mid \ sigma ^ {2}, ja) = {{\ displaystyle n} \text{const}}}$ można przyjąć za μ , a wcześniejszą skalę ${\ Displaystyle p (\ sigma ^ {2} \ mid I) \ propto 1/\ sigma ^{2}}$ można przyjąć za σ ² , to daje twierdzenie Bayesa

${\ Displaystyle {\ rozpocząć {wyrównane} p (\ mu \ mid D, \ sigma ^ {2}, ja) i \ sim N ({\ bar {x}}, \ sigma ^ {2} / n), \ \p(\sigma ^{2}\mid D,I)&\sim \operatorname {Inv-scale-} \chi ^{2}(\nu ,s^{2}),\end{aligned}}}$

rozkład normalny i skalowany odwrotny rozkład chi-kwadrat , gdzie i ${\ displaystyle \ nu = n-1}$

${\ Displaystyle s ^ {2} = \ suma {\ Frac {(x_ {i} - {\ bar {x}}) ^ {2}} {n-1}}.}$

W ten sposób staje się całka marginalizacji

${\ Displaystyle {\ rozpocząć {wyrównane} p (\ mu \ mid D, ja) & \ propto \ int _ {0} ^ {\ infty} {\ Frac {1} {\ sqrt {\ sigma ^ {2}} }}\exp \left(-{\frac {1}{2\sigma ^{2}}}n(\mu -{\bar {x}})^{2}\right)\cdot \sigma ^{ -\nu -2}\exp(-\nu s^{2}/2\sigma ^{2})\,d\sigma ^{2}\\&\propto \int _{0}^{\infty }\sigma ^{-\nu -3}\exp \left(-{\frac {1}{2\sigma ^{2}}}\left(n(\mu -{\bar {x}})^ {2}+\nu s^{2}\right)\right)\,d\sigma ^{2}.\end{aligned}}}$

Można to ocenić $=$$,$ gdzie , dając

${\ Displaystyle dz = - {\ Frac {A} {2 \ sigma ^ {4}}} \, d \ sigma ^ {2},}$

Więc

${\ Displaystyle p (\ mu \ mid D, ja) \ propto A ^ {- (\ nu + 1)/2} \ int _ {0} ^ {\ infty} z ^ {(\ nu -1) / 2 }\exp(-z)\,dz.}$

Ale całka z jest teraz standardową całką Gamma , która daje stałą, wychodząc

${\ Displaystyle {\ rozpocząć {wyrównane} p (\ mu \ mid D, ja) & \ propto A ^ {- (\ nu + 1)/2} \\&\ propto \ lewo (1 + {\ frac {n (\mu -{\bar {x}})^{2}}{\nu s^{2}}}\right)^{-(\nu +1)/2}.\end{wyrównane}}}$

Jest to forma rozkładu t z wyraźnym skalowaniem i przesuwaniem, która zostanie omówiona bardziej szczegółowo w dalszej części poniżej. Można to powiązać ze znormalizowanym t przez podstawienie

${\ Displaystyle t = {\ Frac {\ mu - {\ bar {x}}} {s / {\ sqrt {n}}}}.}$

Powyższe wyprowadzenie zostało przedstawione dla przypadku nieinformacyjnych a priori dla i $displaystyle$$\ sigma ^ {2}}$ ; ale będzie oczywiste, że wszelkie a priori, które prowadzą do połączenia rozkładu normalnego ze skalowanym odwrotnym rozkładem chi-kwadrat, doprowadzą do rozkładu t ze skalowaniem i przesuwaniem dla ${\ Displaystyle P (\ mu \mid D,I)}$ , chociaż parametr skalowania odpowiadający na powyższe będą miały wpływ zarówno wcześniejsze informacje, jak i dane, a nie tylko dane, jak $.$

Charakteryzacja

Jako rozkład statystyki testowej

t - Studenta z stopniami swobody można zdefiniować jako rozkład zmiennej losowej T z ${\ displaystyle \ nu}$

${\ Displaystyle T = {\ Frac {Z} {\ sqrt {V / \ nu}}} = Z {\ sqrt {\ Frac {\ nu} {V}}} ,}$

Gdzie

• Z jest standardową normalną o wartości oczekiwanej 0 i wariancji 1;
• V ma rozkład chi-kwadrat ( χ ² -dystrybucja ) z stopniami swobody ${\ displaystyle \ nu}$ ;
• Z i V są niezależne ;

Inny rozkład definiuje się jako rozkład zmiennej losowej określonej dla danej stałej μ przez

${\ Displaystyle (Z + \ mu) {\ sqrt {\ Frac {\ nu} {V}}}.}$

Ta zmienna losowa ma niecentralny rozkład t z niecentralnym parametrem μ . Rozkład ten jest ważny w badaniach mocy testu t - Studenta .

Pochodzenie

Załóżmy, że X ₁ , ..., X _n są niezależnymi realizacjami zmiennej losowej X , o rozkładzie normalnym , która ma wartość oczekiwaną μ i wariancję σ ² . Pozwalać

${\ Displaystyle {\ overline {X}} _ {n} = {\ Frac {1} {n}} (X_ {1} + \ cdots + X_ {N})}$

być średnią z próby i

${\ Displaystyle S_ {n} ^ {2} = {\ Frac {1} {n-1}} \ suma _ { i=1}^{n}\left(X_{i}-{\overline {X}}_{n}\right)^{2}}$

być nieobciążonym oszacowaniem wariancji z próby. Można pokazać, że zmienna losowa

${\ Displaystyle V = (n-1) {\ Frac {S_ {n} ^ {2}} {\ sigma ^ {2}}}}$

ma rozkład chi-kwadrat $($ według Cochrana ) Łatwo wykazać, że ilość

${\ Displaystyle Z = \ lewo ({\ overline {X}} _ {n} - \ mu \ prawej) {\ Frac {\ sqrt {n}} {\ sigma} }}$

is normally distributed with mean 0 and variance 1, since the sample mean ${\overline {X}}_{n}$ is normally distributed with mean μ and variance σ²/n. Moreover, it is possible to show that these two random variables (the normally distributed one Z and the chi-squared-distributed one V) are independent. Consequently the pivotal quantity

${\ textstyle T \ równoważnik {\ Frac {Z} {\ sqrt {V/\ nu}}} = \ lewo ({\ overline {X }}_{n}-\mu \right){\frac {\sqrt {n}}{S_{n}}},}$

który różni się od Z tym, że dokładne odchylenie standardowe σ jest zastąpione przez zmienną losową S _{n , ma rozkład} t- Studenta, jak zdefiniowano powyżej. Zauważ, że nieznana wariancja populacji σ ² nie pojawia się w T , ponieważ była zarówno w liczniku, jak i mianowniku, więc została anulowana. Gosset intuicyjnie uzyskał podaną powyżej funkcję gęstości prawdopodobieństwa, gdzie $- 1$ jest równa n - 1, a Fisher udowodnił to w 1925 roku.

Rozkład statystyki testowej T zależy od $od$ ale nie μ lub σ ; brak zależności od μ i σ sprawia, że ​​rozkład t jest ważny zarówno w teorii, jak iw praktyce.

Jako maksymalny rozkład entropii

t -Studenta to rozkład prawdopodobieństwa maksymalnej entropii dla zmiennej losowej X dla której ${\ Displaystyle \ nazwa operatora {E} (\ ln (\ nu + X ^ {2}) )}$ jest naprawiony.

Nieruchomości

Chwile

Dla surowych momentów rozkładu t są ${\ displaystyle \ nu > 1}$

${\ Displaystyle \ nazwa operatora {E} (T ^ {k}) = {\ rozpocząć {przypadki} 0 i k {\ tekst {nieparzyste}}, \ quad 0 <k <\ nu \\ {\ Frac {1} {{\ sqrt {\pi}}\Gamma \left({\frac {\nu }{2}}\right)}}\left[\Gamma \left({\frac {k+1}{2}}\right) \Gamma \left({\frac {\nu -k}{2}}\right)\nu ^{\frac {k}{2}}\right]&k{\text{parzysty}},\quad 0< k<\nu .\\\end{przypadki}}}$

Momenty porządku $wyższe$ nie istnieją.

Termin dla nawet k można uprościć , używając właściwości funkcji gamma do ${\ displaystyle 0 <k <\ nu}$

${\ Displaystyle \ nazwa operatora {E} (T ^ {k}) = \ nu ^ {\ Frac {k} {2}} \, \ prod _ {i = 1} ^ {k/2} {\ frac {2i -1}{\nu -2i}}\qquad k{\text{parzysty}},\quad 0<k<\nu .}$

Dla rozkładu t z stopniami swobody oczekiwana wartość wynosi 0, jeśli $displaystyle$$\ nu > 1}$ , a jej wariancja to ${\ displaystyle \ nu > 1} \nu {\nu -2}}}$ jeśli ${\ Displaystyle \ nu > 2}$ . Skośność wynosi 0, jeśli i ν $\ displaystyle \ nu > 3}$ nadmiar kurtozy wynosi ${\ Displaystyle {\ Frac {6} {\ nu -4}}}$ jeśli ${\ Displaystyle \ nu > 4}$ .

Samplowanie Monte Carlo

t - Studenta . Sprawa zależy od tego, czy próbki są wymagane samodzielnie, czy też mają być skonstruowane przez zastosowanie funkcji kwantylowej do jednorodnych próbek ; np. w zastosowaniach wielowymiarowych podstawa zależności od kopuli . W przypadku samodzielnego próbkowania rozszerzenie metody Boxa-Mullera i jej postać biegunowa łatwo się rozkłada. Ma tę zaletę, że równie dobrze stosuje się do wszystkich rzeczywistych dodatnich stopni swobody ν, podczas gdy wiele innych kandydujących metod zawodzi, jeśli ν jest bliskie zeru.

Całka funkcji gęstości prawdopodobieństwa Studenta i wartości p

Funkcja A ( t | ν ) jest całką funkcji gęstości prawdopodobieństwa Studenta, f ( t ) między − t i t , dla t ≥ 0. Daje zatem prawdopodobieństwo, że wartość t mniejsza niż obliczona z zaobserwowanych danych byłaby wystąpić przypadkiem. Dlatego funkcja A ( t | ν ) można wykorzystać do sprawdzenia, czy różnica między średnimi dwóch zestawów danych jest istotna statystycznie, poprzez obliczenie odpowiedniej wartości t i prawdopodobieństwa jej wystąpienia, gdyby dwa zestawy danych zostały pobrane z tej samej populacji. Jest to używane w różnych sytuacjach, szczególnie w testach t . Dla statystyki t , z v stopniami swobody, A ( t | ν ) jest prawdopodobieństwem, że t byłaby mniejsza niż obserwowana wartość, gdyby dwie średnie były takie same (pod warunkiem, że mniejsza średnia zostanie odjęta od większej, tak że t ≥ 0). Można to łatwo obliczyć z skumulowanej funkcji dystrybucji F _v ( t ) rozkładu t :

${\ Displaystyle A (t \ mid \ nu) = F_ { \nu }(t)-F_{\nu }(-t)=1-I_{\frac {\nu }{\nu +t^{2}}}\left({\frac {\nu }{2 }},{\frac {1}{2}}\right),}$

gdzie I _x jest uregulowaną niepełną funkcją beta ( a , b ).

Do testowania hipotez statystycznych ta funkcja jest używana do konstruowania wartości p .

rozkład t- Studenta

Pod względem parametru skalowania σ̂ lub σ̂ ²

$}} }$ Studenta można uogólnić na trzyparametrową rodzinę skali lokalizacji , wprowadzając parametr lokalizacji i parametr skali . ${\ Displaystyle {\ hat {\ mu$ , poprzez relację

${\ Displaystyle X = {\ kapelusz {\ mu}} + {\ kapelusz {\ sigma}} T}$

Lub

${\ Displaystyle T = {\ Frac {X- {\ kapelusz {\ mu}}} {\ kapelusz {\ sigma}}}}$

Oznacza to, że $ma$ t Studenta z $nu }$ stopnie swobody.

Otrzymany niestandaryzowany rozkład t- Studenta ma gęstość zdefiniowaną przez:

${\ Displaystyle p (x \ mid \ nu, {\ kapelusz {\ mu}}, {\ kapelusz {\ sigma}}) = {\ Frac {\ Gamma ({\ Frac {\ nu + 1} {2}} )}{\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu }}{\hat {\sigma }}\,}}\left(1+{\frac {1 }{\nu }}\left({\frac {x-{\hat {\mu }}}{\hat {\sigma }}}\right)^{2}\right)^{-(\nu + 1)/2}}$

Tutaj nie odpowiada odchyleniu standardowemu : nie jest to odchylenie standardowe skalowanego rozkładu t , które może nawet nie istnieć; ${\ Displaystyle {\ hat {\ sigma}}}$ nie jest to też odchylenie standardowe leżącego u podstaw rozkładu normalnego , który jest nieznany. ${\ Displaystyle {\ hat {\ sigma}}}$ po prostu ustawia ogólne skalowanie rozkładu. W wywodzie bayesowskim rozkładu krańcowego nieznanej średniej normalnej ${\ Displaystyle {\ kapelusz {\ mu}}}$ powyżej, ${\ Displaystyle {\ kapelusz {\ sigma}}}$ , jak tutaj użyto, odpowiada ilości ${\ Displaystyle {s / {\ sqrt {n} }}}$ , gdzie

${\ Displaystyle s ^ {2} = \ suma {\ Frac {(x_ {i} - {\ bar {x}}) ^ {2}} {n-1}}. \,}$

Równoważnie rozkład można zapisać jako kwadrat tego parametru skali: ${\ Displaystyle {\ hat {\ sigma}} ^ {2}}$

${\ Displaystyle p (x \ mid \ nu, {\ kapelusz {\ mu}}, {\ kapelusz {\ sigma}} ^ {2}) = {\ Frac {\ Gamma ({\ Frac {\ nu + 1}{2}})}{\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu {\hat {\sigma}}^{2}}}}}\left (1+{\frac {1}{\nu}}{\frac {(x-{\kapelusz {\mu}})^{2}}{{\kapelusz {\sigma}}^{2}}} \right)^{-(\nu +1)/2}}$

Inne właściwości tej wersji dystrybucji to:

${\ Displaystyle {\ rozpocząć {wyrównane} \ nazwa operatora {E} (X) & = {\ kapelusz {\ mu}} i {\ tekst {dla}} \ nu> 1 \\\ nazwa operatora {var} (X) & ={\hat {\sigma }}^{2}{\frac {\nu }{\nu -2}}&{\text{ for }}\nu >2\\\operatorname {tryb} (X)& ={\kapelusz {\mu}}\end{wyrównane}}}$

Rozkład ten wynika z połączenia rozkładu Gaussa ( $rozkład$ normalny ) ze średnią i nieznaną wariancją , z odwrotnym rozkładem gamma umieszczonym nad wariancją z parametrami $\ displaystyle a = \ nu / 2 }$ i ${\ Displaystyle b = \ nu {\ kapelusz {\ sigma}} ^ {2}/2}$ . Innymi słowy, zakłada się, że zmienna losowa X ma rozkład Gaussa z nieznaną wariancją o rozkładzie odwrotnym gamma, a następnie wariancja jest marginalizowana (całkowana). Powodem przydatności tej charakterystyki jest to, że odwrotny rozkład gamma jest sprzężonym wcześniejszym rozkładem wariancji rozkładu Gaussa. W rezultacie niestandaryzowany t- Studenta pojawia się naturalnie w wielu problemach wnioskowania bayesowskiego. Zobacz poniżej.

Równoważnie, ten rozkład wynika z połączenia rozkładu Gaussa z rozkładem skalowanym odwrotnym chi-kwadrat z parametrami i ${\ hat {\ sigma}} ^ {2}$$displaystyle$ . Rozkład skalowany odwrotny chi-kwadrat jest dokładnie tym samym rozkładem co odwrotny rozkład gamma, ale z inną parametryzacją, tj. ${\ Displaystyle \ nu = 2a, \; {\ kapelusz {\ sigma}} ^ {2} = {\ Frac {b} {a}}}$ .

Ta wersja rozkładu t może być przydatna w modelowaniu finansowym. Na przykład Platen i Sidorowicz stwierdzili, że spośród rodziny uogólnionych rozkładów hiperbolicznych ta postać rozkładu t z około 4 stopniami swobody najlepiej pasuje do (logarytmicznego) zwrotu wielu światowych indeksów giełdowych .

Pod względem odwrotnego parametru skalowania λ

Alternatywna parametryzacja w kategoriach odwrotnego parametru skalowania (analogicznie do sposobu, w jaki $precyzja$ jest odwrotnością wariancji), zdefiniowanego przez relację $\ Displaystyle \ lambda = {\ frac { 1}{{\kapelusz {\sigma}}^{2}}}\,}$ . Gęstość jest wtedy dana wzorem:

${\ Displaystyle p (x \ mid \ nu, {\ kapelusz {\ mu}}, \ lambda) = {\ Frac {\ Gamma ({\ Frac {\ nu + 1} {2}})} {\ Gamma ( {\frac {\nu }{2}})}}\left({\frac {\lambda}}{\pi \nu }}\right)^{1/2}\left(1+{\frac {\ lambda (x-{\kapelusz {\mu}})^{2}}{\nu}}\right)^{-(\nu +1)/2}.}$

Inne właściwości tej wersji dystrybucji to:

${\ Displaystyle {\ rozpocząć {wyrównane} \ nazwa operatora {E} (X) & = {\ kapelusz {\ mu}} & & {\ tekst {dla}} \ nu > 1 \\ [5 pkt] \ nazwa operatora {var} ( X)&={\frac {1}{\lambda }}{\frac {\nu }{\nu -2}}&&{\text{ for }}\nu >2\\[5pt]\operatorname {tryb } (X)&={\kapelusz {\mu}}\end{wyrównane}}}$

Rozkład ten wynika z połączenia rozkładu Gaussa ze średnią i nieznaną precyzją (odwrotność wariancji ) $,$ rozkładem gamma ${\ Displaystyle a = \ nu / 2}$ nad precyzją z parametrami i ${\ Displaystyle b = \ nu / (2 \ lambda)}$ . Innymi słowy, zakłada się, że zmienna losowa X ma rozkład normalny z nieznaną precyzją rozkładu jako gamma, a następnie jest on marginalizowany w rozkładzie gamma.

Powiązane dystrybucje

• Jeśli $X} ma rozkład$$Displaystyle$ t Studenta ze swobody, to X ² ma rozkład F : ${\ styl wyświetlania X^{2}\sim \mathrm {F} \left(\nu _{1}=1,\nu _{2}=\nu \right)}$
• Niecentralny , rozkład t uogólnia rozkład t tak aby zawierał parametr lokalizacji. W przeciwieństwie do niestandaryzowanych t , rozkłady niecentralne nie są symetryczne (mediana nie jest tożsama z modą).
• Dyskretny rozkład t - Studenta jest określony przez jego funkcję masy prawdopodobieństwa przy r , która jest proporcjonalna do:
  $${\ Displaystyle \ prod _ {j = 1} ^ {k} {\ Frac {1} {(r + j + a) ^ {2} + b ^ {2}}} \ quad \ quad r = \ ldots, -1,0,1,\ldkropki .}$$
  Tutaj a , b i k są parametrami. Rozkład ten wynika z konstrukcji systemu rozkładów dyskretnych, podobnego do rozkładów Pearsona dla rozkładów ciągłych.
• t można wygenerować , biorąc stosunek zmiennych z rozkładu normalnego do pierwiastka kwadratowego z rozkładu χ ² . Jeśli zamiast rozkładu normalnego użyjemy np. rozkładu Irwina-Halla , otrzymamy w sumie symetryczny rozkład 4-parametrowy, który obejmuje rozkład normalny, jednostajny , trójkątny , Student -t i rozkład Cauchy'ego . Jest to również bardziej elastyczne niż niektóre inne symetryczne uogólnienia rozkładu normalnego.
• t -dystrybucja jest przykładem rozkładu ilorazowego .

Wnioskowanie bayesowskie: rozkład a priori stopni swobody

Załóżmy, że reprezentuje liczbę niezależnie i identycznie rozłożonych próbek pobranych z $= (x_ {1}, \ cdots, x_ {N})}$$\ Displaystyle$ Rozkład t-Studenta

${\ Displaystyle t _ {\ nu} (x) = {\ Frac {\ Gamma \ lewo ({\ Frac {\ nu + 1} {2}} \ prawej)} {{\ sqrt {\ nu \ pi}} \ Gamma \left({\frac {\nu }{2}}\right)}}\left(1+{\frac {x^{2}}{\nu }}\right)^{-{\frac { \nu +1}{2}}},\quad x\in \mathbb {R} .}$

Z wyborem a prior dla stopni swobody , $\ nu}$ jako , wnioskowanie późniejszego rozkładu ν $displaystyle$

${\ Displaystyle \ pi (\ nu | {\ textbf {x}}) = {\ Frac {\ prod t _ {\ nu} (x_ {i}) \ cdot \ pi (\ nu)} {\ int \ prod t_ {\nu }(x_{i})\cdot \pi (\nu )d\nu }},\quad \nu \in \mathbb {R} ^{+}.}$

Porównanie błędu średniokwadratowego między estymatorami Bayesa opartymi na czterech a priorach i estymatorem największej wiarygodności dla stopni swobody. Dane są symulowane na podstawie rozkładu $\ nu _$ ucznia ze stopniami swobody zmieniającymi się od 0 do ${\ displaystyle$ przy wielkości próby (po lewej) i ${\ displaystyle N = 100}$ (po prawej). Niższa wartość MSE oznacza lepszą dokładność.

Niektóre popularne wybory przeorów to:

• Jeffreys przeor

${\ Displaystyle \ pi _ {J} (\ nu) \ propto \ lewo ({\ Frac {\ nu} {\ nu +3}} \ prawo) ^ {1/2} \ lewo (\ psi '\ left({\frac {\nu }{2}}\right)-\psi '\left({\frac {\nu +1}{2}}\right)-{\frac {2(\nu +3 )}{\nu (\nu +1)^{2}}}\right)^{1/2},\quad \nu \in \mathbb {R} ^{+},}$ gdzie ${\ Displaystyle \ psi '(x)}$ reprezentuje funkcję trygamma.

• Wykładniczy wcześniejszy

${\ Displaystyle \ pi _ {E} (\ nu) = Ga(\nu |1,0.1)=\exp(\nu |0.1)={\frac {1}{10}}e^{-\nu /10},\quad \nu \in \mathbb {R} ^{+}}$

• Gamma przed

${\ Displaystyle \ pi _ {G} (\ nu) = Ga (\ nu | 2,0,1 )={\frac {\nu }{100}}e^{-\nu /10},\quad \nu \in \mathbb {R} ^{+}}$

• Log-normal przed

${\ Displaystyle \ pi _ {L} (\ nu) = logN (\ nu | 1,1) = {\ Frac {1} {\ nu {\ sqrt {2 \ pi}}}} \ exp \ lewo [- {\frac {(\log \nu -1)^{2}}{2}}\right],\quad \nu \in \mathbb {R} ^{+}}$

Prawe panele przedstawiają wyniki eksperymentów numerycznych. Estymator Bayesa oparty na a priori Jeffreysa $dla$ błąd średniokwadratowy (MSE) niż estymator największej wiarygodności (MLE ${\ Displaystyle \ nu _ {0} \ w (0,25)}$ . Należy zauważyć, że żaden estymator Bayesa nie dominuje nad innymi estymatorami w przedziale ${\ Displaystyle (0,25)}$ . Innymi słowy, każdy estymator Bayesa ma swój własny region, w którym estymator nie jest gorszy od innych.

Używa

W częstościowym wnioskowaniu statystycznym

t- Studenta pojawia się w różnych problemach estymacji statystycznej, w których celem jest oszacowanie nieznanego parametru, takiego jak wartość średnia, w warunkach, w których dane są obserwowane z błędami addytywnymi . Jeśli (jak w prawie wszystkich praktycznych pracach statystycznych) odchylenie standardowe populacji tych błędów jest nieznane i musi być oszacowane na podstawie danych, rozkład t jest często używany do uwzględnienia dodatkowej niepewności wynikającej z tego oszacowania. W większości takich problemów, gdyby znane było odchylenie standardowe błędów, rozkład normalny byłby używany zamiast rozkładu t .

Przedziały ufności i testy hipotez to dwie procedury statystyczne, w których wymagane są kwantyle rozkładu próbkowania określonej statystyki (np. wyniku standardowego ). W każdej sytuacji, w której ta statystyka jest funkcją liniową danych , podzieloną przez zwykłe oszacowanie odchylenia standardowego, wynikową wielkość można przeskalować i wyśrodkować, aby podążać za rozkładem t- Studenta . Analizy statystyczne obejmujące średnie, średnie ważone i współczynniki regresji prowadzą do statystyk mających tę postać.

t - Studenta . Problemy te są na ogół dwojakiego rodzaju: (1) te, w których wielkość próby jest tak duża, że ​​oszacowanie wariancji oparte na danych można traktować tak, jakby było pewne, oraz (2) te, które ilustrują rozumowanie matematyczne, w których problem oszacowania odchylenia standardowego jest chwilowo ignorowany, ponieważ nie jest to przedmiotem wyjaśniania autora lub instruktora.

Testowanie hipotez

Można wykazać, że wiele statystyk ma rozkłady t dla próbek o średniej wielkości przy hipotezach zerowych , które są przedmiotem zainteresowania, tak że rozkład t stanowi podstawę testów istotności. Na przykład rozkład współczynnika korelacji rang Spearmana ρ w przypadku zerowym (korelacja zerowa) jest dobrze aproksymowany przez rozkład t dla wielkości próbek powyżej około 20.

Przedziały ufności

Załóżmy, że liczba A jest tak dobrana, że

${\ Displaystyle \ Pr (-A <T <A) = 0,9,}$

gdy T ma rozkład t z n - 1 stopniami swobody. Przez symetrię jest to to samo, co stwierdzenie, że A spełnia

${\ Displaystyle \ Pr (T <A) = 0,95,}$

więc A jest „95. percentylem” tego rozkładu prawdopodobieństwa lub ${\ Displaystyle A = t_ {(0,05, n-1)}}$ . Następnie

${\ Displaystyle \ Pr \ lewo (-A <{\ Frac {{\ overline {X}} _ {n} - \ mu} {S_{n}/{\sqrt {n}}}}<A\right)=0.9,}$

a to jest równoważne

${\ Displaystyle \ Pr \ lewo ({\ overline {X}} _ {n} -A {\ frac {S_ {n}}} {\ sqrt {n}}} <\ mu <{\ overline {X}} _ {n}+A{\frac {S_{n}}{\sqrt {n}}}\right)=0.9.}$

Dlatego przedział, którego punkty końcowe są

${\ Displaystyle {\ overline {X}} _ {n} \ pm A {\ Frac {S_ {n}} {\ sqrt {n}}}}$

to 90% przedział ufności dla μ. Dlatego też, jeśli znajdziemy średnią zbioru obserwacji, co do której możemy rozsądnie oczekiwać, że będzie miała rozkład normalny, możemy użyć rozkładu t do zbadania, czy granice ufności tej średniej obejmują jakąś teoretycznie przewidywaną wartość – taką jak przewidywana wartość na hipotezie zerowej .

To właśnie ten wynik jest używany w testach t - Studenta : ponieważ różnica między średnimi próbek z dwóch rozkładów normalnych sama ma rozkład normalny, rozkład t można wykorzystać do sprawdzenia, czy można rozsądnie przyjąć, że różnica wynosi zero .

Jeśli dane mają rozkład normalny, jednostronną (1 - α )-górną granicę ufności (UCL) średniej można obliczyć za pomocą następującego równania:

${\ Displaystyle \ operatorname {UCL} _ {1- \ alfa} = {\ overline {X}} _ {n} + t _ {\ alfa, n-1} {\ Frac {S_ {n}}} {\ sqrt { N}}}.}$

Wynikowy UCL będzie największą średnią wartością, która wystąpi dla danego przedziału ufności i wielkości populacji. Innymi słowy, będąc średnią zbioru obserwacji, prawdopodobieństwo, że średnia rozkładu jest gorsza od UCL _{1- α} , jest równe ${\ displaystyle {\ overline {X}} _ {n}}$ poziom ufności 1 − α .

Przedziały predykcji

Rozkładu t można użyć do skonstruowania przedziału predykcji dla nieobserwowanej próbki z rozkładu normalnego z nieznaną średnią i wariancją.

W statystyce bayesowskiej

t- Studenta , zwłaszcza w wersji trójparametrowej (lokalizacja-skala), często pojawia się w statystyce bayesowskiej w wyniku jego powiązania z rozkładem normalnym . Ilekroć wariancja zmiennej losowej o rozkładzie normalnym jest nieznana, a koniugat uprzedni umieszcza się nad nią, która jest zgodna z odwrotnym rozkładem gamma , wynikowy rozkład krańcowy zmiennej będzie zgodny z t Studenta -dystrybucja. Konstrukcje równoważne z tymi samymi wynikami obejmują sprzężony rozkład skalowany-odwrotność chi-kwadrat na wariancji lub sprzężony rozkład gamma na precyzję . Jeśli nad wariancją zostanie umieszczona niewłaściwa liczba a priori proporcjonalna do σ ^{−2 ,} powstanie również rozkład t . Dzieje się tak niezależnie od tego, czy znana jest średnia zmiennej o rozkładzie normalnym, czy nieznany jest rozkład zgodny ze sprzężeniem rozkład normalny przed lub nieznany rozkład według niewłaściwej stałej wcześniejszej.

Powiązane sytuacje, które również dają rozkład t , to:

• Krańcowy rozkład późniejszy nieznanej średniej zmiennej o rozkładzie normalnym, z nieznaną wcześniejszą średnią i wariancją zgodnie z powyższym modelem .
• Wcześniejszy rozkład predykcyjny i późniejszy rozkład predykcyjny nowego punktu danych o rozkładzie normalnym, gdy zaobserwowano serię niezależnych identycznie rozłożonych punktów danych o rozkładzie normalnym, z wcześniejszą średnią i wariancją, jak w powyższym modelu.

Solidne modelowanie parametryczne

Rozkład t jest często używany jako alternatywa dla rozkładu normalnego jako model danych, który często ma cięższe ogony, niż pozwala na to rozkład normalny; patrz np. Lange i in. Klasyczne podejście polegało na identyfikacji wartości odstających (np. za pomocą testu Grubbsa ) i ich wykluczeniu lub zmniejszeniu ich w jakiś sposób. Jednak nie zawsze łatwo jest zidentyfikować wartości odstające (zwłaszcza w przypadku dużych wymiarów ), a rozkład t jest naturalnym wyborem modelu dla takich danych i zapewnia parametryczne podejście do solidnych statystyk .

Relację Bayesa można znaleźć w Gelman i in. Parametr stopni swobody steruje kurtozą rozkładu i jest skorelowany z parametrem skali. Prawdopodobieństwo może mieć wiele lokalnych maksimów iw związku z tym często konieczne jest ustalenie stopni swobody na dość niskiej wartości i oszacowanie innych parametrów, przyjmując to za podane. Niektórzy autorzy podają, że wartości od 3 do 9 to często dobry wybór. Venables i Ripley sugerują, że wartość 5 jest często dobrym wyborem.

Proces t - Studenta

Na potrzeby praktycznej regresji i predykcji wprowadzono procesy t - Studenta , które są uogólnieniami rozkładów t- Studenta dla funkcji. Proces t - Studenta jest konstruowany z rozkładów t- Studenta , tak jak proces Gaussa jest konstruowany z rozkładów Gaussa . W przypadku procesu Gaussa wszystkie zestawy wartości mają wielowymiarowy rozkład Gaussa. Analogicznie ${\ Displaystyle X (t)} jest procesem$ t Studenta w przedziale ${\ displaystyle I = [a, b]}$ jeśli odpowiednie wartości procesu $, ..., X (t_ {n})}$ ( ${\ Displaystyle t_ {i} \ in I}$ ) mają wspólny wielowymiarowy Student t -dystrybucja . Procesy te są wykorzystywane do regresji, predykcji, optymalizacji bayesowskiej i problemów pokrewnych. W przypadku regresji wielowymiarowej i predykcji wielowymiarowej wprowadza się i stosuje wielowymiarowe procesy t -Studenta.

Tabela wybranych wartości

Poniższa tabela zawiera wartości rozkładów t z v stopniami swobody dla zakresu jednostronnych lub dwustronnych obszarów krytycznych. Pierwsza kolumna to ν , wartości procentowe u góry to poziomy ufności, a liczby w treści tabeli to czynniki opisane w sekcji ${\ displaystyle t _ {\ alfa, n-1}}$ na przedziałach ufności .

Ostatni rząd z nieskończonym v daje punkty krytyczne dla rozkładu normalnego, ponieważ rozkład t z nieskończenie wieloma stopniami swobody jest rozkładem normalnym. (Zobacz Powiązane dystrybucje powyżej).

Jednostronny	75%	80%	85%	90%	95%	97,5%	99%	99,5%	99,75%	99,9%	99,95%
Dwustronny	50%	60%	70%	80%	90%	95%	98%	99%	99,5%	99,8%	99,9%
1	1.000	1.376	1.963	3.078	6.314	12.706	31.821	63.657	127.321	318.309	636.619
2	0,816	1.080	1.386	1.886	2.920	4.303	6.965	9.925	14.089	22.327	31.599
3	0,765	0,978	1.250	1.638	2.353	3.182	4.541	5.841	7.453	10.215	12.924
4	0,741	0,941	1.190	1.533	2.132	2.776	3.747	4.604	5.598	7.173	8.610
5	0,727	0,920	1.156	1.476	2.015	2.571	3.365	4.032	4.773	5.893	6.869
6	0,718	0,906	1.134	1.440	1.943	2.447	3.143	3.707	4.317	5.208	5.959
7	0,711	0,896	1.119	1.415	1.895	2.365	2.998	3.499	4.029	4.785	5.408
8	0,706	0,889	1.108	1.397	1.860	2.306	2.896	3.355	3.833	4.501	5.041
9	0,703	0,883	1.100	1.383	1.833	2.262	2.821	3.250	3.690	4.297	4.781
10	0,700	0,879	1.093	1.372	1.812	2.228	2.764	3.169	3.581	4.144	4.587
11	0,697	0,876	1.088	1.363	1.796	2.201	2.718	3.106	3.497	4.025	4.437
12	0,695	0,873	1.083	1.356	1.782	2.179	2.681	3.055	3.428	3.930	4.318
13	0,694	0,870	1.079	1.350	1.771	2.160	2.650	3.012	3.372	3.852	4.221
14	0,692	0,868	1.076	1.345	1.761	2.145	2.624	2.977	3.326	3.787	4.140
15	0,691	0,866	1.074	1.341	1.753	2.131	2.602	2.947	3.286	3.733	4.073
16	0,690	0,865	1.071	1.337	1.746	2.120	2.583	2.921	3.252	3.686	4.015
17	0,689	0,863	1.069	1.333	1.740	2.110	2.567	2.898	3.222	3.646	3.965
18	0,688	0,862	1.067	1.330	1.734	2.101	2.552	2.878	3.197	3.610	3.922
19	0,688	0,861	1.066	1.328	1.729	2.093	2.539	2.861	3.174	3.579	3.883
20	0,687	0,860	1.064	1.325	1.725	2.086	2.528	2.845	3.153	3.552	3.850
21	0,686	0,859	1.063	1.323	1.721	2.080	2.518	2.831	3.135	3.527	3.819
22	0,686	0,858	1.061	1.321	1.717	2.074	2.508	2.819	3.119	3.505	3.792
23	0,685	0,858	1.060	1.319	1.714	2.069	2500	2.807	3.104	3.485	3.767
24	0,685	0,857	1.059	1.318	1.711	2.064	2.492	2.797	3.091	3.467	3.745
25	0,684	0,856	1.058	1.316	1.708	2.060	2.485	2.787	3.078	3.450	3.725
26	0,684	0,856	1.058	1.315	1.706	2.056	2.479	2.779	3.067	3.435	3.707
27	0,684	0,855	1.057	1.314	1.703	2.052	2.473	2.771	3.057	3.421	3.690
28	0,683	0,855	1.056	1.313	1.701	2.048	2.467	2.763	3.047	3.408	3.674
29	0,683	0,854	1.055	1.311	1.699	2.045	2.462	2.756	3.038	3.396	3.659
30	0,683	0,854	1.055	1.310	1.697	2.042	2.457	2.750	3.030	3.385	3.646
40	0,681	0,851	1.050	1.303	1.684	2.021	2.423	2.704	2.971	3.307	3.551
50	0,679	0,849	1.047	1.299	1.676	2.009	2.403	2.678	2.937	3.261	3.496
60	0,679	0,848	1.045	1.296	1.671	2.000	2.390	2.660	2.915	3.232	3.460
80	0,678	0,846	1.043	1.292	1.664	1.990	2.374	2.639	2.887	3.195	3.416
100	0,677	0,845	1.042	1.290	1.660	1.984	2.364	2.626	2.871	3.174	3.390
120	0,677	0,845	1.041	1.289	1.658	1.980	2.358	2.617	2.860	3.160	3.373
∞	0,674	0,842	1.036	1.282	1.645	1.960	2.326	2.576	2.807	3.090	3.291
Jednostronny	75%	80%	85%	90%	95%	97,5%	99%	99,5%	99,75%	99,9%	99,95%
Dwustronny	50%	60%	70%	80%	90%	95%	98%	99%	99,5%	99,8%	99,9%

Obliczanie przedziału ufności

Załóżmy, że mamy próbę o wielkości 11, średnią próby 10 i wariancję próby 2. Dla 90% pewności z 10 stopniami swobody jednostronna wartość t z tabeli wynosi 1,372. Następnie z przedziałem ufności obliczonym z

${\ Displaystyle {\ overline {X}} _ {n} \ pm t _ {\ alfa, \ nu} {\ Frac {S_ {n}}} {\ sqrt {n }}},}$

stwierdzamy, że z 90% pewnością mamy prawdziwą średnią leżącą poniżej

${\ Displaystyle 10 + 1,372 {\ Frac {\ sqrt {2}} {\ sqrt {11}}} = 10,585.}$

Innymi słowy, w 90% przypadków, gdy górny próg jest obliczany tą metodą z określonych próbek, ten górny próg przekracza prawdziwą średnią.

A przy 90% pewności mamy prawdziwą średnią leżącą powyżej

${\ Displaystyle 10-1.372 {\ Frac {\ sqrt {2}} {\ sqrt {11}}} = 9,414.}$

Innymi słowy, w 90% przypadków, gdy dolny próg jest obliczany tą metodą z określonych próbek, ten niższy próg leży poniżej prawdziwej średniej.

Tak więc przy 80% pewności (obliczonej z 100% - 2 × (1 - 90%) = 80%) mamy prawdziwą średnią leżącą w przedziale

${\ Displaystyle \ lewo (10-1.372 {\ Frac {\ sqrt {2}}} {\ sqrt {11}}}, 10 + 1,372 {\ Frac {\ sqrt {2}} {\ sqrt {11}}} \ prawo)=(9,414,10,585).}$

Stwierdzenie, że w 80% przypadków, gdy górne i dolne progi są obliczane tą metodą z danej próbki, prawdziwa średnia jest zarówno poniżej górnego progu, jak i powyżej dolnego progu, nie jest tym samym, co stwierdzenie, że istnieje 80% prawdopodobieństwo, że prawdziwa średnia leży między konkretną parą górnych i dolnych progów, które zostały obliczone tą metodą; patrz przedział ufności i błąd prokuratora .

Obecnie oprogramowanie statystyczne, takie jak język programowania R i funkcje dostępne w wielu programach arkuszy kalkulacyjnych , obliczają wartości rozkładu t i jego odwrotności bez tablic.

Zobacz też

• F -dystrybucja
• Rozkłady złożone- t i pół- t
• Rozkład T -kwadrat Hotellinga
• Wielowymiarowa dystrybucja Studenta
• Standardowa tabela normalna ( tabela rozkładu Z )
• t -statystyka
• Rozkład Tau dla wewnętrznie studentyzowanych reszt
• Rozkład lambda Wilksa
• Dystrybucja życzeń
• półnormalny z $jest$ podany ${\ Displaystyle f (x) = {\ Frac {2 \ beta ^ {\ Frac {\ alfa} {2}} x ^ {\ alfa -1} \ exp (- \ beta x ^ {2} + \ gamma x )} {\ Psi {\ lewo ({\ frac {\ alfa} {2}}, {\ frac {\ gamma}} {\ sqrt {\ beta}}} \ prawo)}}}} ,$ gdzie ${\ Displaystyle \ Psi (\ alfa, z) = {} _ {1} \ Psi _ {1} \ lewo ({\ rozpocząć {matrix}\left(\alpha ,{\frac {1}{2}}\right)\\(1,0)\end{matrix}};z\right)}$ oznacza Funkcja Psi Foxa-Wrighta .

Notatki

•   Senn S.; Richardson, W. (1994). „Pierwszy t ”. Statystyka w medycynie . 13 (8): 785–803. doi : 10.1002/sim.4780130802 . PMID 8047737 .
•   Hogg RV , Craig AT (1978). Wprowadzenie do statystyki matematycznej (wyd. 4). Nowy Jork: Macmillan. ASIN B010WFO0SA .
• Venables, WN; Ripley, BD (2002). Nowoczesne statystyki stosowane z S (wyd. Czwarte). Skoczek.
•   Gelman, Andrzej; Johna B. Carlina; Hal S. Sterna; Donald B. Rubin (2003). Analiza danych Bayesa (wyd. Drugie). CRC/Chapman & Hall. ISBN 1-58488-388-X .

Linki zewnętrzne

• „Dystrybucja uczniów” , Encyklopedia matematyki , EMS Press , 2001 [1994]
• Najwcześniejsze znane zastosowania niektórych słów matematyki (S) (Uwagi na temat historii terminu „dystrybucja ucznia”)
• Rouaud, M. (2013), Prawdopodobieństwo, statystyki i szacunki (PDF) (red. Skrócona) Pierwsi studenci na stronie 112.
• Rozkład t-Studenta , zarchiwizowane 2021-04-10 w Wayback Machine ck12