Dystrybucja Batesa

Batesa

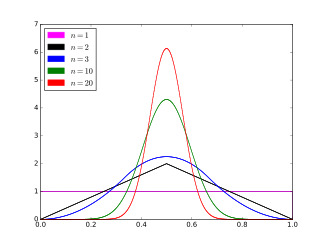
Funkcja gęstości prawdopodobieństwa
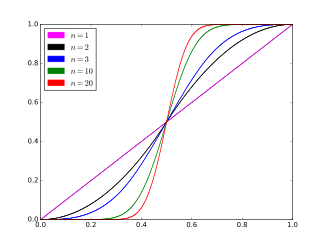
Funkcja dystrybucji skumulowanej
Parametry	${\ Displaystyle - \ infty <a <b <\ infty}$${\ Displaystyle n \ geq 1}$ liczba całkowita
Wsparcie	${\ Displaystyle x \ w [a, b]}$
PDF	patrz poniżej
Mieć na myśli	${\ Displaystyle {\ tfrac {1} {2}} (a + b)}$
Zmienność	${\ Displaystyle {\ tfrac {1} {12n}} (ba) ^ {2}}$
Skośność	0
Były. kurtoza	${\ Displaystyle - {\ tfrac {6} {5n}}}$
CF	${\ Displaystyle \ lewo (- {\ Frac {w (e ^ {\ tfrac {ibt}}}} -e^{\tfrac {iat}{n}}}}{(ba)t}}\right)^{n}}$

W statystyce prawdopodobieństwa i statystyki biznesowej rozkład Batesa , nazwany na cześć Grace Bates , jest rozkładem prawdopodobieństwa średniej liczby statystycznie niezależnych zmiennych losowych o rozkładzie jednorodnym w przedziale jednostkowym . Rozkład ten jest powiązany z jednolitym , trójkątnym i normalnym Gaussa i ma zastosowanie w inżynierii transmisji do wzmacniania sygnału. Rozkład Batesa jest czasami mylony z rozkładem Irwina-Halla , który jest rozkładem sumy ( nie średniej ) n niezależnych zmiennych losowych równomiernie rozłożonych od 0 do 1. Zatem te dwa rozkłady są po prostu wersjami siebie nawzajem, ponieważ różnią się tylko skalą.

Definicja

Rozkład Batesa jest ciągłym rozkładem prawdopodobieństwa średniej , X , n niezależnych , równomiernie rozłożonych zmiennych losowych w przedziale jednostkowym U _k :

${\ Displaystyle X = {\ Frac {1} {n}} \ suma _ {k = 1} ^ {n} U_ {k}.}$

Równanie określające funkcję gęstości prawdopodobieństwa zmiennej losowej X o rozkładzie Batesa to

${\ Displaystyle f_ {X} (x; n) = {\ Frac {n} 2(n-1)!}}\suma _{k=0}^{n}(-1)^{k}{n \wybierz k}(nx-k)^{n-1}\nazwa_operatora {sgn }(nx-k)}$

dla x w przedziale (0,1) i zero gdzie indziej. Tutaj sgn( nx − k ) oznacza funkcję znaku :

${\ Displaystyle \ nazwa operatora {sgn} (nx-k) = {\ rozpocząć {przypadki} -1 & nx <k \\ 0&nx = k \\ 1&nx> k. \ koniec {przypadków}}}$

Mówiąc bardziej ogólnie, średnia n niezależnych zmiennych losowych o rozkładzie równomiernym w przedziale [ a , b ]

${\ Displaystyle X_ {(a, b)} = {\ Frac {1} {n}} \ suma _ {k = 1} ^ {n} U_ {k} (a, b).}$

miałby funkcję gęstości prawdopodobieństwa (PDF)

${\ Displaystyle g (x; n, a, b) = {\ Frac {1}{ba}}f_{X}\left({\frac {xa}{ba}};n\right){\text{ for }}a\równoważnik x\równoważnik b}$

Rozszerzenia i aplikacje

Z kilkoma modyfikacjami rozkład Batesa obejmuje rozkład jednostajny , trójkątny i, przyjmując granicę, gdy n dąży do nieskończoności, także rozkład Gaussa normalnego .

Zastąpienie terminu podczas obliczania średniej X przez ${ \ Displaystyle {\$$sqrt {n}}}}$ podobny rozkład ze stałą wariancją, taką jak jedność. Następnie, odejmując średnią, wynikowa średnia rozkładu zostanie ustalona na zero. W ten sposób parametr n stałby się parametrem czysto dopasowującym kształt . Dopuszczając również, n było liczbą niecałkowitą, można utworzyć wysoce elastyczny rozkład, na przykład U (0,1) + 0,5 U (0,1) daje rozkład trapezoidalny .

Rozkład t-Studenta zapewnia naturalne rozszerzenie normalnego rozkładu Gaussa do modelowania danych z długim ogonem . Rozkład Batesa, który został uogólniony, jak stwierdzono wcześniej, spełnia ten sam cel dla z krótkim ogonem .

Dystrybucja Batesa ma zastosowanie do kształtowania wiązki i syntezy wzorców w dziedzinie elektrotechniki. Stwierdzono, że rozkład zwiększa szerokość wiązki głównego płata , reprezentując wzrost sygnału charakterystyki promieniowania w jednym kierunku, przy jednoczesnym zmniejszeniu, zwykle niepożądanych poziomów listków bocznych .

Zobacz też

• Dystrybucja Irwina-Halla
• Normalna dystrybucja
• Centralne twierdzenie graniczne
• Jednolita dystrybucja (ciągła)
• Dystrybucja trójkątna

Dalsza lektura

• Bates, GE (1955) „Wspólne rozkłady przedziałów czasowych występowania kolejnych wypadków w uogólnionym schemacie urn Polya”, Annals of Mathematical Statistics , 26, 705–720