Miara prawdopodobieństwa

W matematyce miara prawdopodobieństwa to funkcja o wartościach rzeczywistych zdefiniowana na podstawie zbioru zdarzeń w przestrzeni prawdopodobieństwa , która spełnia właściwości miary , takie jak przeliczalna addytywność . Różnica między miarą prawdopodobieństwa a bardziej ogólnym pojęciem miary (które obejmuje pojęcia takie jak powierzchnia lub objętość ) polega na tym, że miara prawdopodobieństwa musi przypisać wartość 1 całej przestrzeni prawdopodobieństwa.

Intuicyjnie właściwość addytywności mówi, że prawdopodobieństwo przypisane sumie dwóch rozłącznych zdarzeń według miary powinno być sumą prawdopodobieństw zdarzeń; na przykład wartość przypisana „1 lub 2” w rzucie kostką powinna być sumą wartości przypisanych do „1” i „2”.

Miary prawdopodobieństwa mają zastosowanie w różnych dziedzinach, od fizyki po finanse i biologię.

Definicja

Miara prawdopodobieństwa $na$ przestrzeń prawdopodobieństwa przedział jednostkowy .

Wymagania, aby funkcja była miarą prawdopodobieństwa w przestrzeni prawdopodobieństwa, są następujące: ${\ displaystyle \ mu}$

• $mu }$ zwrócić wyniki w przedziale jednostkowym ${\ Displaystyle [0,1],}$${\ displaystyle \$ { $\ displaystyle 0}$ dla pustego zestawu i dla całej przestrzeni μ .
• musi spełniać ${i} \}}$ addytywności , która dla wszystkich przeliczalnych zbiorów zbiorów parami rozłącznych : $ja$
  $${\ Displaystyle \ mu \ lewo (\ bigcup _ {i \ in \ mathbb {N}} E_ {i} \ prawo) = \ suma _ {i \ in \ mathbb {N}} \ mu (E_ {i}) .}$$

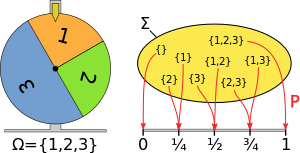
$4,1/$$/$ , ${\ Displaystyle \ {1,3 \}}$ 3 z prawdopodobieństwami i przypisaną do jest $1/4 + 1/2 = 3/4,}$ prawej .

Prawdopodobieństwo warunkowe oparte na przecięciu zdarzeń zdefiniowanych jako:

$${\ Displaystyle \ mu (B \ środek A) = {\ Frac {\ mu (A \ czapka B)} {\ mu (A)}}.}$$

$,$ o ile nie wynosi zero

Miary prawdopodobieństwa różnią się od bardziej ogólnego pojęcia miar rozmytych , w którym nie ma wymogu, aby wartości rozmyte sumowały się do $właściwość$ dodatku została zastąpiona relacją porządku opartą na włączeniu zbioru .

Przykładowe zastosowania

W wielu przypadkach fizyka statystyczna wykorzystuje miary prawdopodobieństwa , ale nie wszystkie stosowane przez nią miary są miarami prawdopodobieństwa.

Miary rynkowe , które przypisują prawdopodobieństwa przestrzeniom rynków finansowych w oparciu o rzeczywiste ruchy rynku, są przykładami miar prawdopodobieństwa interesujących w finansach matematycznych ; na przykład przy wycenie finansowych instrumentów pochodnych . Na przykład miara neutralna pod względem ryzyka to miara prawdopodobieństwa, która zakłada, że ​​bieżąca wartość aktywów jest oczekiwaną wartością przyszłej wypłaty w odniesieniu do tej samej miary neutralnej pod względem ryzyka (tj. obliczoną przy użyciu odpowiedniej funkcji gęstości neutralnej pod względem ryzyka), oraz przeceniony po stopie wolnej od ryzyka . Jeśli istnieje unikalna miara prawdopodobieństwa, której należy użyć do wyceny aktywów na rynku, wówczas rynek ten nazywa się rynkiem pełnym .

Nie wszystkie miary, które intuicyjnie reprezentują szansę lub prawdopodobieństwo, są miarami prawdopodobieństwa. Na przykład, chociaż podstawowym pojęciem układu w mechanice statystycznej jest przestrzeń miar, miary takie nie zawsze są miarami prawdopodobieństwa. Ogólnie rzecz biorąc, w fizyce statystycznej, jeśli weźmiemy pod uwagę zdania w postaci „prawdopodobieństwo układu S przy założeniu stanu A wynosi p”, geometria układu nie zawsze prowadzi do zdefiniowania miary prawdopodobieństwa w ramach kongruencji , chociaż może to zrobić tak jest w przypadku układów o tylko jednym stopniu swobody.

Miary prawdopodobieństwa są również stosowane w biologii matematycznej . Na przykład w porównawczej analizie sekwencji można zdefiniować miarę prawdopodobieństwa dla prawdopodobieństwa, że ​​wariant może być dopuszczalny dla aminokwasu w sekwencji.

Ultrafiltry można rozumieć jako miary prawdopodobieństwa o wartościach wartościowych, pozwalające na wiele intuicyjnych $dowodów$ Na przykład twierdzenie Hindmana można udowodnić na podstawie dalszego badania tych miar, a w szczególności ich splotu .

Zobacz też

• Miara borelowa – miara zdefiniowana na wszystkich otwartych zbiorach przestrzeni topologicznej
• Miara rozmyta – teoria miar uogólnionych, w której właściwość addytywną zastępuje się słabszą właściwością monotoniczności. Strony wyświetlające opisy wikidanych jako rozwiązanie awaryjne
• Miara Haara – miara niezmienna po lewej stronie (lub niezmienna po prawej stronie) w lokalnie zwartej grupie topologicznej Strony wyświetlające opisy wikidanych jako rozwiązanie awaryjne
• Miara Lebesgue’a – Pojęcie pola w dowolnym wymiarze
• Miara Martingale – miara prawdopodobieństwa Strony wyświetlające krótkie opisy celów przekierowań
• Funkcja ustawiania – funkcja od zestawów do liczb

Dalsza lektura

•   Billingsley, Patrick (1995). Prawdopodobieństwo i miara . Johna Wileya. ISBN 0-471-00710-2 .
•   Ash, Robert B.; Doléans-Dade, Catherine A. (1999). Prawdopodobieństwo i teoria miary . Prasa akademicka. ISBN 0-12-065202-1 .

Linki zewnętrzne

• Media związane z miarą prawdopodobieństwa w Wikimedia Commons