Pasmo przenoszenia

W przetwarzaniu sygnałów i elektronice odpowiedź częstotliwościowa systemu jest ilościową miarą wielkości i fazy sygnału wyjściowego w funkcji częstotliwości wejściowej. Pasmo przenoszenia jest szeroko stosowane w projektowaniu i analizie systemów, takich jak audio i systemy sterowania , gdzie upraszczają analizę matematyczną, przekształcając rządzące równania różniczkowe w równania algebraiczne . W systemie audio może być używany do minimalizowania słyszalnych zniekształceń projektując komponenty (takie jak mikrofony , wzmacniacze i głośniki ) w taki sposób, aby ogólna odpowiedź była jak najbardziej płaska (jednolita) w całym paśmie systemu . W systemach sterowania, takich jak tempomat pojazdu , może być używany do oceny stabilności systemu , często za pomocą wykresów Bodego . Systemy o określonej charakterystyce częstotliwościowej mogą być projektowane przy użyciu analogowych i cyfrowych .

Odpowiedź częstotliwościowa charakteryzuje systemy w dziedzinie częstotliwości , podobnie jak odpowiedź impulsowa charakteryzuje systemy w dziedzinie czasu . W systemach liniowych każda odpowiedź całkowicie opisuje system, a zatem ma zgodność jeden do jednego: odpowiedź częstotliwościowa jest transformatą Fouriera odpowiedzi impulsowej. Pasmo przenoszenia umożliwia prostszą analizę systemów kaskadowych, takich jak wzmacniacze wielostopniowe , ponieważ odpowiedź całego systemu można znaleźć poprzez pomnożenie odpowiedzi częstotliwościowych poszczególnych stopni (w przeciwieństwie do splotu odpowiedzi impulsowej w dziedzinie czasu). Odpowiedź częstotliwościowa jest ściśle związana z funkcją przenoszenia w układach liniowych, która jest transformatą Laplace'a odpowiedzi impulsowej. Są równoważne, gdy część rzeczywista $jest$ zespolonej funkcji przenoszenia ${\ Displaystyle s = \ sigma + j \ omega}$ wynosi zero.

Pomiar i kreślenie

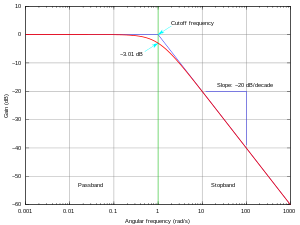
Odpowiedź amplitudowa filtra dolnoprzepustowego z 6 dB na oktawę lub 20 dB na dekadę

Pomiar odpowiedzi częstotliwościowej zwykle obejmuje wzbudzenie systemu sygnałem wejściowym i pomiar wynikowego sygnału wyjściowego, obliczenie widma częstotliwości dwóch sygnałów (na przykład przy użyciu szybkiej transformaty Fouriera dla sygnałów dyskretnych) i porównanie widm w celu wyizolowania efektu systemu. W systemach liniowych zakres częstotliwości sygnału wejściowego powinien pokrywać interesujący nas zakres częstotliwości.

Do pomiaru odpowiedzi częstotliwościowej systemu można zastosować kilka metod wykorzystujących różne sygnały wejściowe, w tym:

Zastosowano sinusoidy o stałej amplitudzie przechodzące przez zakres częstotliwości i porównując amplitudę i przesunięcie fazowe sygnału wyjściowego względem sygnału wejściowego. Przemiatanie częstotliwości musi być wystarczająco wolne, aby system osiągnął stan ustalony w każdym punkcie zainteresowania
Podanie sygnału impulsowego i obliczenie transformaty Fouriera odpowiedzi układu
Zastosowanie stacjonarnego białego szumu o szerokim zasięgu przez długi okres czasu i obliczenie odpowiedzi systemu na transformatę Fouriera. W tej metodzie należy użyć gęstości widma krzyżowego (zamiast gęstości widma mocy ), jeśli wymagane są informacje o fazie

Odpowiedź częstotliwościowa jest charakteryzowana wielkością , zazwyczaj w decybelach (dB) lub jako ogólna amplituda zmiennej zależnej, a faza , w radianach lub stopniach, mierzona względem częstotliwości, w radianach/s , hercach (Hz) lub jako ułamek częstotliwości próbkowania .

Istnieją trzy popularne sposoby wykreślania pomiarów odpowiedzi:

Bode wykreśla wykres wielkości i fazy w funkcji częstotliwości na dwóch prostokątnych wykresach
Nyquist wykreśla wykres wielkości i fazy parametrycznie względem częstotliwości w postaci biegunowej
Nichols wykreśla wykres wielkości i fazy parametrycznie względem częstotliwości w formie prostokąta

Do projektowania systemów sterowania można zastosować dowolny z trzech typów wykresów, aby wywnioskować stabilność i marginesy stabilności w pętli zamkniętej na podstawie odpowiedzi częstotliwościowej w pętli otwartej. W wielu zastosowaniach w dziedzinie częstotliwości (takich jak systemy audio) odpowiedź fazowa jest stosunkowo nieistotna, a odpowiedź amplitudowa na wykresie Bodego może być wszystkim, co jest wymagane. W systemach cyfrowych (takich jak filtry cyfrowe ) pasmo przenoszenia często zawiera główny płat z wieloma okresowymi listkami bocznymi, z powodu wycieku widmowego spowodowanego procesami cyfrowymi, takimi jak próbkowanie i okienkowanie .

Nieliniowa odpowiedź częstotliwościowa

Jeśli badany system jest nieliniowy , liniowa analiza w dziedzinie częstotliwości nie ujawni wszystkich nieliniowych charakterystyk. Aby przezwyciężyć te ograniczenia, zdefiniowano uogólnione funkcje odpowiedzi częstotliwościowej i nieliniowe funkcje wyjściowej odpowiedzi częstotliwościowej w celu analizy nieliniowych efektów dynamicznych. Metody nieliniowej odpowiedzi częstotliwościowej mogą ujawnić efekty takie jak rezonans , intermodulacja i transfer energii .

Aplikacje

W elektronice bodziec ten byłby sygnałem wejściowym. W zakresie słyszalności mówi się o nim zazwyczaj w połączeniu ze wzmacniaczami elektronicznymi , mikrofonami i głośnikami . Odpowiedź częstotliwościowa widma radiowego może odnosić się do pomiarów kabla koncentrycznego , skrętki , sprzętu przełączającego wideo , urządzeń komunikacji bezprzewodowej i systemów antenowych. Pomiary odpowiedzi częstotliwościowej infradźwięków obejmują trzęsienia ziemi i elektroencefalografię (fale mózgowe).

Wymagania dotyczące odpowiedzi częstotliwościowej różnią się w zależności od zastosowania. W przypadku o wysokiej wierności wzmacniacz wymaga pasma przenoszenia co najmniej 20–20 000 Hz z tolerancją tak wąską, jak ± 0,1 dB w zakresie średnich częstotliwości około 1000 Hz; jednak w telefonii pasmo przenoszenia 400–4 000 Hz z tolerancją ± 1 dB jest wystarczające dla zrozumiałości mowy.

Krzywe odpowiedzi częstotliwościowej są często używane do wskazania dokładności elementów lub systemów elektronicznych. Kiedy system lub komponent odtwarza wszystkie pożądane sygnały wejściowe bez wzmacniania lub tłumienia określonego pasma częstotliwości, mówi się, że system lub komponent jest „płaski” lub ma płaską krzywą odpowiedzi częstotliwościowej. W innym przypadku możemy użyć trójwymiarowej formy powierzchni odpowiedzi częstotliwościowej.

Po zmierzeniu odpowiedzi częstotliwościowej (np. jako odpowiedzi impulsowej), pod warunkiem, że system jest liniowy i niezmienny w czasie , jego charakterystykę można aproksymować z dowolną dokładnością za pomocą filtra cyfrowego . Podobnie, jeśli okaże się, że system ma słabą odpowiedź częstotliwościową, filtr cyfrowy lub analogowy do sygnałów przed ich odtworzeniem, aby zrekompensować te braki.

Kształt krzywej odpowiedzi częstotliwościowej jest bardzo ważny dla ochrony przeciwzakłóceniowej radarów , systemów komunikacyjnych i innych.

Zobacz też

Notatki

Bibliografia

Luter, Arch C.; Inglis, Andrew F. Inżynieria wideo , McGraw-Hill, 1999. ISBN 0-07-135017-9
Starka, Scotta Huntera. Wzmocnienie dźwięku na żywo , Vallejo, Kalifornia, Artistpro.com, 1996–2002. ISBN 0-918371-07-4
LR Rabiner i B. Gold. Teoria i zastosowanie cyfrowego przetwarzania sygnałów. – Englewood Cliffs, NJ: Prentice-Hall, 1975. – 720 s.

Linki zewnętrzne

University of Michigan : Analiza odpowiedzi częstotliwościowej i samouczek projektowania zarchiwizowane 2012-10-17 w Wayback Machine
Smith, Julius O. III: Introduction to Digital Filters with Audio Applications zawiera fajny rozdział poświęcony pasmu przenoszenia