Źródło prądowe Widlara

oryginalnego patentu Widlara

Źródło prądowe Widlara to modyfikacja podstawowego dwutranzystorowego zwierciadła prądowego , która zawiera rezystor degeneracyjny emitera tylko dla tranzystora wyjściowego, umożliwiając źródłu prądowemu generowanie niskich prądów przy użyciu jedynie umiarkowanych wartości rezystorów.

Układ Widlara można zastosować z tranzystorami bipolarnymi , tranzystorami MOS , a nawet lampami próżniowymi . Przykładowym zastosowaniem jest wzmacniacz operacyjny 741 , a Widlar używał tego układu jako części w wielu projektach.

Obwód ten nosi imię jego wynalazcy, Boba Widlara , i został opatentowany w 1967 roku.

Analiza prądu stałego

Rysunek 1: Wersja źródła prądu Widlara wykorzystująca tranzystory bipolarne.

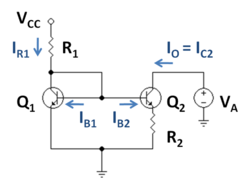
Figura 1 przedstawia przykładowe źródło prądowe Widlara wykorzystujące tranzystory bipolarne, gdzie rezystor emiterowy R2 _jest połączony z tranzystorem wyjściowym Q2 _i powoduje zmniejszenie prądu w _Q2 względem _Q1 . _{Kluczem do tego obwodu jest to, że spadek napięcia} na rezystorze R2 odejmuje od napięcia baza-emiter tranzystora Q2 , tym samym wyłączając ten tranzystor w porównaniu z tranzystorem Q1 . Ta obserwacja jest wyrażona przez zrównanie wyrażeń napięcia podstawowego po obu stronach obwodu na rysunku 1 jako:

${\ Displaystyle {\ rozpocząć {wyrównane} & V_ {B} = V_ {BE1} = V_ {BE2} + (\ beta _ {2} + 1) I_ {B2} R_ {2} \\\ Strzałka w prawo {} & { \frac {1}{R_{2}}}\left(V_{BE1}-V_{BE2}\right)=(\beta _{2}+1)I_{B2}\ ,\end{wyrównane}} }$

gdzie β ₂ jest wartością beta tranzystora wyjściowego, która nie jest taka sama jak wartość tranzystora wejściowego, po części dlatego, że prądy w obu tranzystorach są bardzo różne. Zmienna I _B2 jest prądem bazowym tranzystora wyjściowego, V _BE odnosi się do napięcia baza-emiter. To równanie implikuje (przy użyciu równania diody Shockleya ):

równanie 1

${\ Displaystyle {\ rozpocząć {wyrównane} (\ beta _ {2} + 1) I_ {B2} & = \ lewo (1 + {\ Frac {1} {\ beta _ {2}}} \ prawej) I_ { C2}={\frac {1}{R_{2}}}\left(V_{BE1}-V_{BE2}\right)\\&={\frac {V_{\text{T}}}{R_ {2}}}\left[\ln \left(I_{C1}/I_{S1}\right)-\ln \left(I_{C2}/I_{S2}\right)\right]={\frac {V_{\text{T}}}{R_{2}}}\ln \left({\frac {I_{C1}I_{S2}}{I_{C2}I_{S1}}}\right)\ ,\koniec {wyrównane}}}$

gdzie V _T jest napięciem termicznym .

To równanie przybliża, że ​​oba prądy są znacznie większe niż prądy skali , I _S1 i I _S2 ; przybliżenie ważne, z wyjątkiem obecnych poziomów bliskich odcięciu . Poniżej zakłada się, że prądy skali są identyczne; w praktyce musi to być specjalnie zorganizowane.

Procedura projektowania z określonymi prądami

_Aby zaprojektować zwierciadło, prąd wyjściowy musi być powiązany z dwoma wartościami _rezystorów R1 i R2 . Podstawową obserwacją jest to, że tranzystor wyjściowy jest w stanie aktywnym tylko tak długo, jak długo jego napięcie na bazie kolektora jest niezerowe. _Zatem najprostszy warunek polaryzacji dla konstrukcji zwierciadła ustawia przyłożone napięcie _VA na równe napięciu bazowemu VB . Ta minimalna użyteczna wartość V _A nazywana jest napięciem podatności źródła prądu. Z tym warunkiem odchylenia, Wczesny efekt nie odgrywa żadnej roli w projekcie.

Te rozważania sugerują następującą procedurę projektową:

• Wybierz żądany prąd wyjściowy, I _O = I _C2 .
• Wybierz prąd odniesienia I _R1 , który jest większy niż prąd wyjściowy, prawdopodobnie znacznie większy (taki jest cel układu).
• Wyznacz wejściowy prąd kolektora Q ₁ , I _C1 :

${\ Displaystyle I_ {C1} = {\ Frac {\ beta _ {1}} {\ beta _ {1} + 1}} \ lewo (I_ {R1} - {\ Frac {I_ {C2}} {\ beta _{2}}}\right)\ .}$

• Wyznacz napięcie bazy V _BE1 korzystając z prawa diody Shockleya

$ja$

gdzie _ _S to parametr urządzenia, czasami nazywany prądem skali .

Wartość napięcia bazowego określa również napięcie zgodności V _A = V _BE1 . Napięcie to jest najniższym napięciem, dla którego lustro działa prawidłowo.

• Wyznacz R ₁ :

${\ Displaystyle R_ {1} = {\ Frac {V_ {CC} -V_ {A}} {I_ {R1}}} \ .}$

• Określ opór nogi emitera R ₂ za pomocą równania. 1 prądy skali są równe):

${\ Displaystyle R_ {2} = {\ Frac {V_ {\ tekst {T}}} {\ lewo (1 + {\ Frac {1} {\ beta _ {2}}} \ prawej) I_ {C2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\right)\ .}$

Znalezienie prądu przy danych wartościach rezystorów

Odwrotnością problemu projektowego jest znalezienie prądu, gdy znane są wartości rezystorów. Poniżej opisano metodę iteracyjną. _, że źródło prądu jest spolaryzowane, więc napięcie bazy kolektora tranzystora wyjściowego Q2 wynosi zero. Prąd przepływający przez _R1 jest prądem wejściowym lub prądem odniesienia podanym jako,

${\ Displaystyle {\ rozpocząć {wyrównane} I_ {R1} & = I_ {C1} + I_ {B1} + I_ {B2} \\& = I_ {C1} + {\ Frac {I_ {C1}} {\ beta _{1}}}+{\frac {I_{C2}}{\beta _{2}}}\\&={\frac {1}{R_{1}}}\left(V_{CC}- V_{BE1}\right)\end{aligned}}}$

Przestawiając, I _C1 znajduje się jako:

równanie 2

$\ Displaystyle I_ {C1} = {\ Frac {\ beta _ {1}} {\ beta _{1}+1}}\left({\frac {V_{CC}-V_{BE1}}{R_{1}}}-{\frac {I_{C2}}{\beta _{2}} }\Prawidłowy)}$

Równanie diody zapewnia:

równanie 3

${\ Displaystyle V_ {BE1} = V _ {\ tekst {T}} \ ln \ lewo ({\ Frac {I_ {C1}} {I_ {S1}}} \ prawej) \ .}$

Równanie 1 zapewnia:

${\ Displaystyle I_ {C2} = {\ Frac {V_ {\ tekst {T}}} {\ lewo (1 + {\ Frac {1} {\ beta _ {2}}} \ prawej) R_ {2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\right)\ .}$

Te trzy relacje są nieliniowym, niejawnym określeniem prądów, które można rozwiązać za pomocą iteracji.

• Zgadujemy wartości początkowe dla I _C1 i I _C2 .
• Znajdujemy wartość dla V _BE1 :

  ${\ Displaystyle V_ {BE1} = V _ {\ tekst {T}} \ ln \ lewo ({\ Frac {I_ {C1}} {I_ {S1}}} \ prawej) \ .}$

• Znajdujemy nową wartość dla ja _do1 :

  $} = {\ Frac {\ beta _{1}}{\beta_{1}+1}}\left({\frac {V_{CC}-V_{BE1}}{R_{1}}}-{\frac {I_{C2} }{\beta_{2}}}\prawo)}$

• Znajdujemy nową wartość dla I _C2 :

  ${\ Displaystyle I_ {C2} = {\ Frac {V_ {\ tekst {T}}} {\ lewo (1 + {\ Frac {1} {\ beta _ {2}}} \ prawej) R_ {2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\right)\ .}$

Ta procedura jest powtarzana do konwergencji i jest wygodnie konfigurowana w arkuszu kalkulacyjnym. Wystarczy użyć makra, aby skopiować nowe wartości do komórek arkusza kalkulacyjnego zawierających wartości początkowe w celu uzyskania rozwiązania w krótkim czasie.

Należy zauważyć, że w obwodzie pokazanym na rysunku, jeśli zmieni się V _CC , zmieni się prąd wyjściowy. Stąd, _aby utrzymać stały prąd wyjściowy pomimo wahań V _CC , obwód powinien być zasilany ze źródła prądu stałego , a nie z rezystora R1 .

Dokładne rozwiązanie

równania transcendentalne można rozwiązać dokładnie za pomocą funkcji W Lamberta .

Impedancja wyjściowa

Rysunek 2: Obwód małosygnałowy do znajdowania rezystancji wyjściowej źródła Widlara pokazanego na rysunku 1. Na wyjściu jest przykładany prąd testowy I _{x , a rezystancja wyjściowa wynosi wtedy} R _O = V _x / I _x .

Ważną właściwością źródła prądowego jest impedancja wyjściowa przyrostu małego sygnału, która w idealnym przypadku powinna być nieskończona. Obwód Widlara wprowadza lokalne sprzężenie zwrotne $prądu$ . Jakikolwiek wzrost prądu w _Q2 zwiększa spadek napięcia na R2 , zmniejszając VBE _dla Q2 , przeciwdziałając w ten _sposób wzrostowi prądu _. To sprzężenie zwrotne oznacza, że ​​impedancja wyjściowa obwodu jest zwiększona, ponieważ sprzężenie zwrotne obejmujące R ₂ wymusza użycie większego napięcia do napędzania danego prądu.

Rezystancję wyjściową oblicza się za pomocą modelu małosygnałowego dla obwodu, pokazanego na rysunku 2. Tranzystor _{Q1 jest zastępowany jego rezystancją emitera małosygnałowego rE} , ponieważ jest połączony diodą _. Tranzystor Q ₂ zostaje zastąpiony jego modelem hybrydowym pi . Na wyjściu dołączony jest _prąd testowy Ix .

Korzystając z rysunku, rezystancję wyjściową określa się za pomocą praw Kirchhoffa. Korzystając z prawa napięcia Kirchhoffa od masy po lewej stronie do uziemienia R ₂ :

${\ Displaystyle I_ {b} \ lewo [(R_ {1} \ równolegle r_ {E}) + r_ {\ pi} \ prawo] + [I_ {x} + I_ {b}] R_ {2} = 0 \ .}$

Zmiana kolejności:

${\ Displaystyle I_ {b} = - I_ {x} {\ Frac {R_ {2}} {(R_ {1} \ równoległy r_ {E}) + r_ {\ pi} + R_ {2}}} \ . }$

Korzystając z prawa napięciowego Kirchhoffa od uziemienia R ₂ do uziemienia prądu testowego:

${\ Displaystyle V_ {x} = I_ {x} (R_ {2} + r_ {O}) + I_ { b}(R_{2}-\beta r_{O})\ ,}$

, zastępując Ib _:

równanie 4

  ${\ Displaystyle R_ {O} = {\ Frac {V_ {x}} {I_ { x}}}=r_{O}\left[1+{\frac {\beta R_{2}}{(R_{1}\równoległy r_{E})+r_{\pi}+R_{2}} }\prawo]}$${\ Displaystyle + \ R_ {2} \ lewo [{\ Frac {(R_ {1} \ równoległy r_ {E}) + r_ {\ pi}} {(R_ {1} \ równoległy R_ {E}) + r_ {\pi}+R_{2}}}\prawo]\ .}$

Zgodnie z równaniem 4 , rezystancja wyjściowa źródła prądowego Widlara jest zwiększona w stosunku do rezystancji samego tranzystora wyjściowego (czyli r _O ) tak długo, jak R ₂ jest wystarczająco duży w porównaniu z r _π tranzystora wyjściowego (duże rezystancje R ₂ sprawiają, że współczynnik mnożąc r _O zbliż się do wartości (β + 1)). Tranzystor wyjściowy przewodzi niski prąd, przez co r _{π jest duże, a} R ₂ wzrasta ma tendencję do dalszego zmniejszania tego prądu, powodując skorelowany wzrost r _π . Dlatego cel R ₂ ≫ r _π może być nierealny, a dalsza dyskusja znajduje się poniżej . Rezystancja R ₁ ∥ r _E jest zwykle niewielka, ponieważ rezystancja emitera r _E wynosi zwykle tylko kilka omów.

Aktualna zależność rezystancji wyjściowej

Rysunek 3: Kompromis projektowy między rezystancją wyjściową a prądem wyjściowym. Górny panel: Rezystancja wyjściowa obwodu R _O w funkcji prądu wyjściowego DC I _C2 przy użyciu wzoru równania . 5 dla R2 ; _{_} Panel środkowy: Rezystancja R _O2 w nóżce emitera tranzystora wyjściowego; Panel dolny: Współczynnik sprzężenia zwrotnego wpływający na rezystancję wyjściową. Prąd w tranzystorze odniesienia Q ₁ jest utrzymywany na stałym poziomie, ustalając w ten sposób napięcie zgodności. Wykresy zakładają, że I _C1 = 10 mA, V _A = 50 V, V _CC = 5 V, I _S = 10 fA, β _{1, 2} = 100 niezależnie od prądu.

Bieżąca zależność rezystancji r _π i r _O jest omówiona w artykule model hybrydowy-pi . Aktualna zależność wartości rezystorów to:

${\ Displaystyle R_ {\ pi} = {\ Frac {v_ {być}}} {i_ {b}}} {\ Bigg |} _ {v_ {ce}=0}={\frac {V_{\text{T}}}{I_{\text{B2}}}}=\beta _{2}{\frac {V_{\text{T}} }{ja_{\text{C2}}}}\ ,}$

I

$\ Displaystyle r_ {O} = {\ Frac {v_ {ce}} {i_ {c}}} {\ Bigg |} _ {v_ {be} = 0} = { \frac {V_{A}}{I_{C2}}}}$

to rezystancja wyjściowa spowodowana efektem wczesny , gdy V _CB = 0 V (parametr urządzenia V _A to napięcie wczesne).

Z wcześniejszej części tego artykułu (ustawienie równych prądów skali dla wygody): Eq. 5

${\ Displaystyle R_ {2} = {\ Frac {V_ {\ tekst {T}}} {\ lewo (1 + {\ Frac {1} {\ beta _ {2}}} \ prawej) I_ {C2}} }\ln \left({\frac {I_{C1}}{I_{C2}}}\right)\ .}$

_konsekwencji , dla zwykłego przypadku małego r _E i pomijając drugi wyraz w RO z oczekiwaniem, że człon wiodący obejmujący r _O jest znacznie większy: Równanie. 6

${\ Displaystyle {\ rozpocząć {wyrównane} R_ {O} & \ około r_ {O} \ lewo (1 + {\ Frac {\ beta _ {2} R_ {2}} {r_ {\ pi} + R_ {2 }}}\right)\\&=r_{O}\left(1+{\frac {\beta _{2}\ln \left({\frac {I_{C1}}{I_{C2}}} \right)}{\beta _{2}+1+\ln \left({\frac {I_{C1}}{I_{C2}}}\right)}}\right)\end{wyrównane}}}$

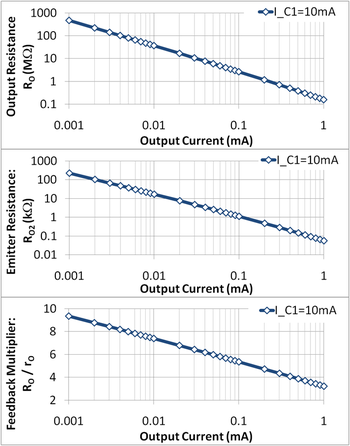
gdzie ostatnią formę można znaleźć, podstawiając Eq. 5 za R ₂ . równanie 6 pokazuje, że wartość rezystancji wyjściowej znacznie większa od rO tranzystora wyjściowego występuje tylko dla układów z I _C1 >> I _{C2 .} Rysunek 3 pokazuje, że rezystancja wyjściowa obwodu R _O jest określana nie tyle przez sprzężenie zwrotne, ile przez aktualną zależność rezystancji r _O tranzystora wyjściowego (rezystancja wyjściowa na rysunku 3 zmienia się o cztery rzędy wielkości, podczas gdy współczynnik sprzężenia zwrotnego zmienia się tylko o jeden rząd wielkości).

Zwiększenie I _C1 w celu zwiększenia współczynnika sprzężenia zwrotnego skutkuje również wzrostem napięcia podatności, co nie jest dobrą rzeczą, ponieważ oznacza to, że źródło prądu działa w bardziej ograniczonym zakresie napięcia. Tak więc, na przykład, _mając ustawiony cel zgodności napięcia, ustalając górną granicę IC1 i mając cel, jakim jest osiągnięcie rezystancji wyjściowej, maksymalna wartość prądu wyjściowego _IC2 jest ograniczona.

Środkowy panel na rysunku 3 pokazuje kompromis projektowy między rezystancją nogi emitera a prądem wyjściowym: niższy prąd wyjściowy wymaga większego rezystora nogi, a tym samym większej powierzchni dla projektu. Górna granica obszaru wyznacza zatem dolną granicę prądu wyjściowego i górną granicę rezystancji wyjściowej obwodu.

równanie 6 dla RO _{zależy od wybrania} wartości R2 zgodnie z równaniem. 5 . To znaczy Równ. 6 nie jest wzorem zachowania obwodu , ale równaniem wartości projektowej . Po wybraniu R2 _{dla określonego celu projektowego za pomocą} równania. 5 , następnie jego wartość jest ustalona. Jeśli działanie obwodu powoduje odchylenia prądów, napięć lub temperatur od wartości przewidzianych; następnie przewidzieć zmiany RO spowodowane takimi odchyleniami _, równanie Należy użyć 4 , a nie Eq. 6 .

Zobacz też

• Obecne źródło
• Obecne lustro
• Obecne źródło Wilsona

Dalsza lektura

•   Linden T. Harrison (2005). Źródła prądu i odniesienia do napięcia: odniesienie projektowe dla inżynierów elektroników . Elsevier-Newnes. ISBN 0-7506-7752-X .
•   Sundaram Natarajan (2005). Mikroelektronika: analiza i projektowanie . Tata McGraw-Hill. P. 319. ISBN 0-07-059096-6 .
• Bieżące lustra i aktywne obciążenia: Mu-Huo Cheng