3-4-6-12 układanie płytek

3-4-6-12 układanie płytek

Typ	2-jednolita płytka
Konfiguracja wierzchołków	3.4.6.4 i 4.6.12
Symetria	p6m, [6,3], (*632)
Symetria obrotu	p6, [6,3] ⁺ , (632)
Nieruchomości	2-jednolity, 4- izoedryczny , 4- izotoksalny

W geometrii płaszczyzny euklidesowej układ 3-4-6-12 jest jednym z 20 2-jednolitych nachyleń płaszczyzny euklidesowej przez wielokąty foremne , zawierające trójkąty foremne , kwadraty , sześciokąty i dwunastokąty , ułożone w konfiguracji dwóch wierzchołków : 3.4. 6.4 i 4.6.12.

Ma symetrię heksagonalną , p6m, [6,3], (*632). Niektórzy autorzy nazywają to również półregularnym kafelkiem .

Geometria

Jego dwie konfiguracje wierzchołków są wspólne dla dwóch 1-jednolitych nachyleń:

dachówka rombtriheksagonalna	obcięte triheksagonalne kafelki
3.4.6.4	4.6.12

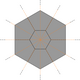
Można to postrzegać jako rodzaj pomniejszonego rombittriheksagonalnego kafelka , z dwunastokątami zastępującymi okresowe zestawy sześciokątów i otaczających je kwadratów i trójkątów. Jest to podobne do bryły Johnsona , zmniejszonego rombicosidodecahedru , który jest rombicosidodecahedronem z usuniętymi ścianami, co prowadzi do nowych dziesięciokątnych ścian. Podwójny wariant tego wariantu jest pokazany po prawej stronie (sześciokątne wstawki naramienne).

Powiązane k -jednolite nachylenia wielokątów foremnych

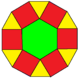
Sześciokąty można podzielić na 6 trójkątów, a dwunastokąty można podzielić na trójkąty, sześciokąty i kwadraty.

Rozcięte wielokąty
Sześciokąt	Dodecagon (każdy ma 2 orientacje)


Podwójne procesy (podwójne „wstawki”)

3-jednolite płytki
48	26	18 (2-mundur)
[3 ⁶ ; 3 ² .4.3.4; 3 ² .4.12]	[3,4 ^2,6 ; (3.4.6.4) ² ]	[3 ⁶ ; 3 ² .4.3.4]
V[3 ⁶ ; 3 ² .4.3.4; 3 ² .4.12]	V[3,4 ^2,6 ; (3.4.6.4) ² ]	V[3 ⁶ ; 3 ² .4.3.4]
3-jednolite podwójne

Pakowanie w kółko

Ta 2-jednolita płytka może być używana jako opakowanie okrągłe . Cyjanowe okręgi stykają się z 3 innymi okręgami (2 cyjan, 1 różowy), odpowiadającymi planigowi V4.6.12, a różowe okręgi stykają się z 4 innymi okręgami (1 cyjan, 2 różowe), odpowiadającym planigonowi V3.4.6. 4 planigony. Jest homeomorficzny z operacją ambo na kafelkach, z cyjanowymi i różowymi wielokątami przerwy odpowiadającymi cyjanowym i różowym kółkom (wielokąty konfiguracji mini-wierzchołków; jednowymiarowe liczby podwójne do odpowiednich planigonów). Oba obrazy pokrywają się.


C [3.4.6.12]	a[3.4.6.12]

Podwójne układanie płytek

Podwójne płytki mają trójkąty prostokątne i powierzchnie latawca , zdefiniowane przez konfiguracje ścian : V3.4.6.4 i V4.6.12, i można je zobaczyć jako połączenie trójkątnych płytek naramiennych i płytek kisrhombille .

Podwójne układanie płytek	V3.4.6.4 V4.6.12	Deltoidalne triheksagonalne płytki	Płytki Kisrhombille

Notatki

Keith Critchlow, Order in Space: A design source book , 1970, s. 62–67
Ghyka, M. The Geometry of Art and Life , (1946), wydanie 2, New York: Dover, 1977. Płytki półregularne # 15
Williams, Robert (1979). Geometryczne podstawy naturalnej struktury: źródłowa księga projektowania . Dover Publications, Inc. ISBN 0-486-23729-X . s. 35–43
Grünbaum, Branko ; Shephard, GC (1987). Płytki i wzory . WH Freemana. ISBN 0-7167-1193-1 . P. 65
Sacred Geometry Design Sourcebook: Universal Dimensional Patterns , Bruce Rawles, 1997. s. 36–37 [1]

Linki zewnętrzne

Chavey, D. (1989). „Pochylenia według regularnych wielokątów - II: Katalog położeń” . Komputery i matematyka z aplikacjami . 17 : 147–165. doi : 10.1016/0898-1221(89)90156-9 .
Holenderski, Steve. „Jednolite Dachówki” . Zarchiwizowane od oryginału w dniu 2006-09-09 . Źródło 2006-09-09 .
Weisstein, Eric W. „Tesselacja półregularna” . MathWorld .
W poszukiwaniu półregularnych nachyleń , Helmer Aslaksen
n -uniform tilings Brian Galebach, 2-uniform tiling 1 z 20