Absorbujący łańcuch Markowa

Przykładem absorbującego łańcucha Markowa jest chód (skończonego) pijaka .

W matematycznej teorii prawdopodobieństwa łańcuch Markowa pochłaniający to łańcuch Markowa , w którym każdy stan może osiągnąć stan pochłaniający. Stan absorbujący to stan, w który raz wkroczy się i nie można go opuścić.

Podobnie jak ogólne łańcuchy Markowa, mogą istnieć łańcuchy Markowa pochłaniające czas ciągły z nieskończoną przestrzenią stanów. Jednak ten artykuł koncentruje się na przypadku dyskretnej przestrzeni stanów w czasie dyskretnym.

Definicja formalna

Łańcuch Markowa jest łańcuchem absorbującym, jeśli

1. istnieje co najmniej jeden stan absorbujący i
2. możliwe jest przejście z dowolnego stanu do co najmniej jednego stanu pochłaniającego w skończonej liczbie kroków.

W absorbującym łańcuchu Markowa stan, który nie jest absorbujący, nazywany jest przejściowym.

Forma kanoniczna

Niech absorbujący łańcuch Markowa z macierzą przejść P ma t stanów przejściowych i r stanów absorbujących. W przeciwieństwie do typowej macierzy przejść, wiersze P reprezentują źródła, podczas gdy kolumny reprezentują miejsca docelowe. Następnie

${\ Displaystyle P = {\ rozpocząć {bmatrix} Q&R \\\ mathbf {0} & I_ {r} \ koniec {bmatrix}},}$

0 gdzie Q jest macierzą t -by- t , R jest niezerową macierzą t -by- r , jest macierzą r -by- t zero, a I _r jest macierzą tożsamości r -by- r . Zatem Q opisuje prawdopodobieństwo przejścia z jednego stanu przejściowego do innego, podczas gdy R opisuje prawdopodobieństwo przejścia z pewnego stanu przejściowego do stanu pochłaniającego.

Prawdopodobieństwo przejścia z i do j w dokładnie k krokach to ( ⁱ , j ) -wejściowa Pk , obliczona dalej poniżej. Biorąc pod uwagę tylko stany przejściowe, prawdopodobieństwo znalezione w lewym górnym rogu P ^k , wejście ( i , j ) Q ^k .

Matryca fundamentalna

Oczekiwana liczba wizyt w stanie przejściowym

Podstawową właściwością absorbującego łańcucha Markowa jest oczekiwana liczba odwiedzin stanu przejściowego j, począwszy od stanu przejściowego i (przed wchłonięciem). Można to ustalić na podstawie wpisu ( i , j ) tzw. macierzy fundamentalnej N , otrzymanej przez zsumowanie Q ^k dla wszystkich k (od 0 do ∞). Można to udowodnić

${\ Displaystyle N: = \ suma _ {k = 0} ^ {\ infty} Q ^ {k} = (I_ {t} - P)^{-1},}$

gdzie I _t jest t -bajtową macierzą identyczności. Obliczenie tego wzoru jest macierzystym odpowiednikiem szeregu geometrycznego skalarów:

${\ Displaystyle \ suma _ {k = 0} ^ {\ infty} q ^ {k} = {\ tfrac {1} {1-q}} = (1-q) ^ {-1}.}$

Mając w ręku macierz N , można łatwo uzyskać także inne własności łańcucha Markowa.

Oczekiwana liczba kroków przed wchłonięciem

Oczekiwaną liczbę kroków przed wchłonięciem w dowolnym stanie pochłaniania, gdy rozpoczyna się stan przejściowy i, można obliczyć za pomocą sumy stanów przejściowych. Wartość jest podawana w i- tym wpisie wektora

${\ Displaystyle \ mathbf {t}: = N \ mathbf {1},}$

gdzie 1 to wektor kolumnowy długości- t , którego wszystkie wpisy są równe 1.

Absorpcja prawdopodobieństw

przez indukcję,

${\ Displaystyle P ^ {k} = {\ rozpocząć {bmatrix} Q ^ {k} i (1-Q ^ {k}) NR \\\ mathbf {0} & I_ {r} \ koniec {bmatrix}}.}$

Prawdopodobieństwo ostatecznego pochłonięcia w stanie pochłaniania j , gdy zaczyna się od stanu przejściowego i, jest określone przez wejście ( i , j ) macierzy

${\ Displaystyle B: = NR}$ .

Liczba kolumn tej macierzy jest równa liczbie stanów absorbujących r .

Przybliżenie tych prawdopodobieństw można również uzyskać bezpośrednio z wejścia ( ja , jot $)$ dla wystarczająco dużej wartości k , kiedy i indeksem stanu przejściowego, a wskaźnik stanu absorbującego. To dlatego, że

${\ Displaystyle \ lewo (\ lim _ {k \ do \ infty} P ^ {k} \ prawej) _ {i, t + j} =B_{i,j}}$ .

Przejściowe prawdopodobieństwa odwiedzin

Prawdopodobieństwo przejścia do stanu przejściowego j przy rozpoczynaniu od stanu przejściowego i to wejście ( i , j ) macierzy

${\ Displaystyle H: = (NI_ {t}) (N _ {\ nazwa operatora {dg}}) ^ {- 1},}$

gdzie N _dg jest macierzą diagonalną o tej samej przekątnej co N .

Wariancja liczby wizyt przejściowych

Wariancja liczby wejść do stanu przejściowego j rozpoczynającego się od stanu przejściowego i (przed wchłonięciem) to ( i , j )-wejście macierzy

${\ Displaystyle N_ {2}: = N (2N _ {\ operatorname {dg}} -I_ {t}) -N _ {\ operatorname {sq} },}$

gdzie N _sq jest iloczynem Hadamarda N z samym sobą (tj. każdy wpis N jest podniesiony do kwadratu).

Różnice w liczbie kroków

Wariancja liczby kroków przed wchłonięciem, gdy startuje się ze stanu przejściowego i, to i- ta pozycja wektora

${\ Displaystyle (2N-I_ {t}) \ mathbf {t} - \ mathbf {t} _ {\ operatorname {sq}},}$

gdzie t _sq jest iloczynem Hadamarda t z samym sobą (tj. tak jak w przypadku N _sq , każdy wpis t jest podniesiony do kwadratu).

Przykłady

Generowanie ciągów

Główny artykuł: generowanie ciągów

Rozważ proces wielokrotnego rzucania uczciwą monetą , aż pojawi się sekwencja (orzeł, reszka, orzeł). Proces ten jest modelowany przez absorbujący łańcuch Markowa z macierzą przejść

${\ Displaystyle P = {\ początek {bmatrix} 1/2&1/2&0&0 \\0&1/2&1/2&0 \\1/2&0&0&1/2\\0&0&0&1\koniec {bmatrix}}.}$

Pierwszy stan reprezentuje pusty ciąg znaków , drugi stan łańcucha „H”, trzeci stan łańcucha „HT”, a czwarty stan łańcucha „HTH”. Chociaż w rzeczywistości rzuty monetą ustają po wygenerowaniu ciągu „HTH”, perspektywa absorbującego łańcucha Markowa jest taka, że ​​proces przeszedł do stanu pochłaniania reprezentującego ciąg „HTH” i dlatego nie może wyjść.

Dla tego absorbującego łańcucha Markowa podstawową macierzą jest

${\ Displaystyle {\ rozpocząć {wyrównane} N & = (IQ) ^ {- 1} = \ lewo ({\ rozpocząć {bmatrix} 1 i 0 i 0 \\ 0 i 1 i 0 \\ 0 i 0 i 1 \ koniec {bmatrix}} - {\ rozpocząć {bmatrix} 1 /2&1/2&0\\0&1/2&1/2\\1/2&0&0\end{bmatrix}}\right)^{-1}\\[4pt]&={\begin{bmatrix}1/2&-1/2&0 \\0&1/2&-1/2\\-1/2&0&1\end{bmatrix}}^{-1}={\begin{bmatrix}4&4&2\\2&4&2\\2&2&2\end{bmatrix}}.\end{ wyrównany}}}$

Oczekiwana liczba kroków rozpoczynających się od każdego ze stanów przejściowych wynosi

${\ Displaystyle \ mathbf {t} = N \ mathbf {1} = {\ początek {bmatrix} 4 i 4 i 2 \\ 2 i 4 i 2 \\ 2 i 2 i 2 \ koniec {bmatrix}} {\ początek {bmatrix} 1 \\1 \\ 1 \ koniec {bmacierz}}={\rozpocznij{bmacierz}10\\8\\6\koniec{bmacierz}}.}$

Dlatego oczekiwana liczba rzutów monetą przed obserwacją sekwencji (orzeł, reszka, orzeł) wynosi 10, wpis dla stanu reprezentującego pusty ciąg.

Skumulowane prawdopodobieństwo zakończenia gry Snakes and Ladders po kolei N

Gry losowe

Gry całkowicie oparte na przypadku mogą być modelowane przez absorbujący łańcuch Markowa. Klasycznym tego przykładem jest starożytna indyjska gra planszowa Węże i drabiny . Wykres po lewej przedstawia masę prawdopodobieństwa w samotnym stanie pochłaniania, który reprezentuje ostatni kwadrat, gdy macierz przejścia jest podnoszona do coraz większych potęg. Aby określić oczekiwaną liczbę tur wymaganych do zakończenia gry, oblicz wektor t w sposób opisany powyżej i zbadaj t _start , które wynosi w przybliżeniu 39,2.

Testy na choroby zakaźne

Testy na choroby zakaźne, czy to produktów krwiopochodnych, czy w klinikach medycznych, są często nauczane jako przykład absorbującego łańcucha Markowa. Na przykład publiczny model Amerykańskich Centrów Kontroli i Prewencji Chorób (CDC) dotyczący HIV i wirusowego zapalenia wątroby typu B ilustruje właściwość polegającą na tym, że wchłanianie łańcuchów Markowa może prowadzić do wykrycia choroby, w przeciwieństwie do utraty wykrycia za pomocą innych środków.

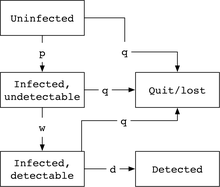
W standardowym modelu CDC łańcuch Markowa ma pięć stanów, stan, w którym osoba jest niezainfekowana, następnie stan z zainfekowanym, ale niewykrywalnym wirusem, stan z wykrywalnym wirusem i absorbujące stany wyjścia/zagubienia z kliniki, lub wykrycia (cel). Typowe szybkości przejść między stanami Markowa to prawdopodobieństwo p na jednostkę czasu zarażenia wirusem, w dla szybkości usuwania okresu okna (czas do wykrycia wirusa), q dla szybkości opuszczania/utraty z systemu oraz d do wykrywania, zakładając typową szybkość, $opieki$ zdrowotnej przeprowadza testy danego produktu krwiopochodnego lub pacjentów.

Klasyczny przykład modelu badań przesiewowych w kierunku HIV lub wirusa zapalenia wątroby

Wynika z tego, że możemy „spacerować” po modelu Markowa, aby określić ogólne prawdopodobieństwo wykrycia osoby startującej jako niewykrytej, mnożąc prawdopodobieństwa przejścia do każdego kolejnego stanu modelu jako:

${\ Displaystyle {\ Frac {p} {(p + q)}} {\ Frac {w} {(w + q)}}} \frac {d}{(d+q)}}}$ .

Późniejsza całkowita bezwzględna liczba fałszywie ujemnych testów – główny problem CDC – byłaby wtedy wskaźnikiem testów pomnożonym przez prawdopodobieństwo osiągnięcia zainfekowanego, ale niewykrywalnego stanu, razy czas pozostawania w zainfekowanym, niewykrywalnym stanie:

${\ Displaystyle {\ Frac {p} {(p + q)}} {\ Frac {1} {(w + q)}} \ lambda}$ .

Zobacz też

• Dyskretny rozkład fazowy
• Zbiór absorbujący (losowe układy dynamiczne)

Linki zewnętrzne

• Projekt demonstracyjny Wolframa: Wchłanianie łańcucha Markowa
• Monopol jako łańcuch Markowa