Algorytm generowania labiryntu

Algorytmy generowania labiryntów to zautomatyzowane metody tworzenia labiryntów .

ten labirynt wygenerowany przez zmodyfikowaną wersję algorytmu Prim .

Metody oparte na teorii grafów

Animacja metody opartej na teorii grafów (randomizowane przeszukiwanie w głąb)

Labirynt można wygenerować, zaczynając od z góry określonego układu komórek (najczęściej prostokątnej siatki, ale możliwe są inne układy) ze ścianami między nimi. Ten z góry określony układ można uznać za połączony graf z krawędziami reprezentującymi możliwe lokalizacje ścian i węzłami reprezentującymi komórki. Można zatem uznać, że celem algorytmu generowania labiryntu jest utworzenie podgrafu, w którym trudno jest znaleźć trasę między dwoma określonymi węzłami.

Jeśli podgraf nie jest spójny , to są regiony grafu, które są marnowane, ponieważ nie mają udziału w przestrzeni poszukiwań. Jeśli wykres zawiera pętle, może istnieć wiele ścieżek między wybranymi węzłami. Z tego powodu generowanie labiryntu jest często traktowane jako generowanie losowego drzewa rozpinającego . Pętle, które mogą zmylić naiwnych rozwiązujących labirynt, można wprowadzić, dodając losowe krawędzie do wyniku w trakcie algorytmu.

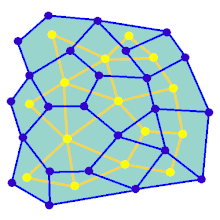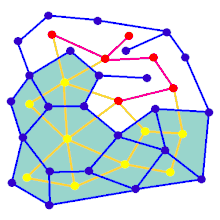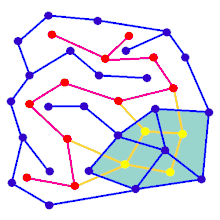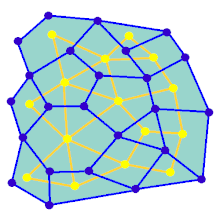
Animacja pokazuje etapy generowania labiryntu dla wykresu, który nie jest na prostokątnej siatce. Najpierw komputer tworzy losowy graf planarny G pokazany na niebiesko i jego podwójny F pokazany na żółto. Po drugie, komputer przemierza F przy użyciu wybranego algorytmu, takiego jak przeszukiwanie w głąb, kolorując ścieżkę na czerwono. Podczas przechodzenia, gdy czerwona krawędź przecina niebieską krawędź, niebieska krawędź jest usuwana. Wreszcie, kiedy wszystkie wierzchołki F zostały odwiedzone, F jest wymazywane, a dwie krawędzie z G, jedna dla wejścia i jedna dla wyjścia, są usuwane.

Randomizowane przeszukiwanie w głąb

Animacja generatora przy użyciu wyszukiwania w głąb
Inna animacja generatora wykorzystującego przeszukiwanie w głąb

Algorytm ten, znany również jako algorytm „rekurencyjnego śledzenia wstecznego”, jest losową wersją algorytmu przeszukiwania w głąb .

To podejście, często realizowane ze stosem, jest jednym z najprostszych sposobów generowania labiryntu za pomocą komputera. Rozważ przestrzeń labiryntu jako dużą siatkę komórek (jak duża szachownica), z których każda zaczyna się od czterech ścian. Zaczynając od losowej komórki, komputer następnie wybiera losowo sąsiednią komórkę, która nie została jeszcze odwiedzona. Komputer usuwa ścianę między dwiema komórkami i oznacza nową komórkę jako odwiedzoną, a następnie dodaje ją do stosu, aby ułatwić cofanie się. Komputer kontynuuje ten proces, a komórka, która nie ma nieodwiedzonych sąsiadów, jest uważana za ślepą uliczkę. Kiedy znajduje się w ślepym zaułku, cofa się ścieżką, aż dotrze do komórki z nieodwiedzonym sąsiadem, kontynuując generowanie ścieżki, odwiedzając tę ​​nową, nieodwiedzoną komórkę (tworząc nowe skrzyżowanie). Proces ten trwa do momentu odwiedzenia każdej komórki, co powoduje, że komputer cofa się aż do komórki początkowej. Możemy być pewni, że każda komórka jest odwiedzana.

Jak podano powyżej, ten algorytm obejmuje głęboką rekurencję, która może powodować problemy z przepełnieniem stosu w niektórych architekturach komputerów. Algorytm można przekształcić w pętlę, przechowując informacje o śledzeniu wstecznym w samym labiryncie. Zapewnia to również szybki sposób wyświetlenia rozwiązania, rozpoczynając od dowolnego punktu i cofając się do początku.

Poziome odchylenie przejścia

Labirynty generowane z przeszukiwaniem w głąb mają niski współczynnik rozgałęzień i zawierają wiele długich korytarzy, ponieważ algorytm bada jak najdalej wzdłuż każdej gałęzi przed cofnięciem.

Implementacja rekurencyjna

Randomizowane przeszukiwanie w głąb na sześciokątnej siatce

Algorytm przeszukiwania w głąb generowania labiryntu jest często implementowany przy użyciu śledzenia wstecznego . Można to opisać za pomocą następującej rekurencyjnej :

  1. Biorąc pod uwagę bieżącą komórkę jako parametr
  2. Zaznacz bieżącą komórkę jako odwiedzoną
  3. Podczas gdy bieżąca komórka ma nieodwiedzone sąsiednie komórki
    1. Wybierz jednego z nieodwiedzonych sąsiadów
    2. Usuń ścianę między bieżącą komórką a wybraną komórką
    3. Wywołaj procedurę rekurencyjnie dla wybranej komórki

która jest wywoływana raz dla dowolnej początkowej komórki w obszarze.

Implementacja iteracyjna

Wadą pierwszego podejścia jest duża głębokość rekurencji – w najgorszym przypadku procedura może wymagać powtórzenia w każdej komórce przetwarzanego obszaru, co w wielu środowiskach może przekroczyć maksymalną głębokość stosu rekurencji. Jako rozwiązanie, ta sama metoda śledzenia wstecznego może być zaimplementowana z jawnym stosem , który zwykle może znacznie wzrosnąć bez szkody.

  1. Wybierz komórkę początkową, oznacz ją jako odwiedzoną i włóż na stos
  2. Podczas gdy stos nie jest pusty
    1. Zdejmij komórkę ze stosu i ustaw ją jako bieżącą komórkę
    2. Jeśli bieżąca komórka ma sąsiadów, którzy nie zostali odwiedzeni
      1. Przenieś bieżącą komórkę na stos
      2. Wybierz jednego z nieodwiedzonych sąsiadów
      3. Usuń ścianę między bieżącą komórką a wybraną komórką
      4. Zaznacz wybraną komórkę jako odwiedzoną i odłóż ją na stos

Randomizowany algorytm Kruskala

Animacja generowania labiryntu 30 na 20 przy użyciu algorytmu Kruskala.

Algorytm ten jest losową wersją algorytmu Kruskala .

  1. Utwórz listę wszystkich ścian i utwórz zestaw dla każdej komórki, z których każda zawiera tylko tę jedną komórkę.
  2. Dla każdej ściany, w przypadkowej kolejności:
    1. Jeśli komórki podzielone tą ścianą należą do różnych zestawów:
      1. Usuń obecną ścianę.
      2. Połącz zestawy wcześniej podzielonych komórek.

Istnieje kilka struktur danych, których można użyć do modelowania zestawów komórek. Wydajna implementacja wykorzystująca rozłączną strukturę danych zbiorach w prawie stałym czasie ( szczególności w czasie; dla dowolnej wiarygodnej wartości ), więc czas działania tego algorytmu jest zasadniczo proporcjonalny do liczby ścian dostępnych dla labiryntu.

Nie ma większego znaczenia, czy lista ścian jest początkowo losowa, czy też ściana jest losowo wybierana z nielosowej listy, w obu przypadkach kodowanie jest równie łatwe.

Ponieważ efektem tego algorytmu jest utworzenie minimalnego drzewa rozpinającego z grafu o jednakowo ważonych krawędziach, ma on tendencję do tworzenia regularnych wzorców, które są dość łatwe do rozwiązania.

Randomizowany algorytm Prima

Animacja generowania labiryntu 30 na 20 przy użyciu algorytmu Prim.

Algorytm ten jest losową wersją algorytmu Prima .

  1. Zacznij od siatki pełnej ścian.
  2. Wybierz komórkę, zaznacz ją jako część labiryntu. Dodaj ściany komórki do listy ścian.
  3. Podczas gdy na liście znajdują się ściany:
    1. Wybierz losową ścianę z listy. Jeśli odwiedzana jest tylko jedna komórka, którą dzieli ściana, to:
      1. Zrób w ścianie przejście i zaznacz nieodwiedzoną celę jako część labiryntu.
      2. Dodaj sąsiednie ściany komórki do listy ścian.
    2. Usuń ścianę z listy.

Zauważ, że po prostu uruchomienie klasycznego Prima na grafie z losowymi wagami krawędzi stworzyłoby labirynty stylistycznie identyczne z labiryntami Kruskala, ponieważ oba są algorytmami minimalnego drzewa rozpinającego. Zamiast tego ten algorytm wprowadza zróżnicowanie stylistyczne, ponieważ krawędzie bliżej punktu początkowego mają niższą efektywną wagę.

Zmodyfikowana wersja

Chociaż klasyczny algorytm Prima przechowuje listę krawędzi, w przypadku generowania labiryntu moglibyśmy zamiast tego zachować listę sąsiadujących komórek. Jeśli losowo wybrana komórka ma wiele krawędzi, które łączą ją z istniejącym labiryntem, wybierz losowo jedną z tych krawędzi. Będzie to miało tendencję do rozgałęziania się nieco bardziej niż powyższa wersja oparta na krawędziach.

Wersja uproszczona

Algorytm można jeszcze bardziej uprościć, wybierając losowo komórki sąsiadujące z już odwiedzonymi komórkami, zamiast śledzić wagi wszystkich komórek lub krawędzi.

Zwykle stosunkowo łatwo będzie znaleźć drogę do komórki początkowej, ale trudno będzie znaleźć drogę gdziekolwiek indziej.

Algorytm Wilsona

Główny artykuł: błądzenie losowe z wymazywaniem pętli
Animacja generowania labiryntu przy użyciu algorytmu Wilsona (szary reprezentuje trwający losowy spacer). Po zbudowaniu labirynt jest rozwiązywany przy użyciu wyszukiwania w głąb

Wszystkie powyższe algorytmy mają różnego rodzaju odchylenia: przeszukiwanie w głąb jest ukierunkowane na długie korytarze, podczas gdy algorytmy Kruskala/Prim są ukierunkowane na wiele krótkich ślepych zaułków. Z drugiej strony algorytm Wilsona generuje nieobciążoną próbkę z jednolitego rozkładu we wszystkich labiryntach, używając losowych spacerów z wymazywaniem pętli .

Algorytm zaczynamy od zainicjowania labiryntu z jedną dowolnie wybraną komórką. Następnie zaczynamy od dowolnie wybranej nowej komórki i wykonujemy błądzenie losowe, aż dotrzemy do komórki znajdującej się już w labiryncie — jeśli jednak w dowolnym momencie błądzenie losowe dotrze do własnej ścieżki, tworząc pętlę, usuwamy pętlę ze ścieżki przed kontynuowaniem. Kiedy ścieżka dotrze do labiryntu, dodajemy ją do labiryntu. Następnie wykonujemy kolejny losowy spacer z wymazaną pętlą z innej dowolnej komórki początkowej, powtarzając, aż wszystkie komórki zostaną wypełnione.

Ta procedura pozostaje bezstronna bez względu na to, jakiej metody użyjemy do arbitralnego wyboru komórek początkowych. Więc zawsze możemy wybrać pierwszą niewypełnioną komórkę w kolejności (powiedzmy) od lewej do prawej, od góry do dołu dla uproszczenia.

Algorytm Aldousa-Brodera

Algorytm Aldousa-Brodera tworzy również jednolite drzewa rozpinające.

  1. Wybierz losową komórkę jako komórkę bieżącą i oznacz ją jako odwiedzoną.
  2. Podczas gdy istnieją nieodwiedzone komórki:
    1. Wybierz losowego sąsiada.
    2. Jeżeli wybrany sąsiad nie był odwiedzany:
      1. Usuń ścianę między obecną komórką a wybranym sąsiadem.
      2. Zaznacz wybranego sąsiada jako odwiedzonego.
    3. Uczyń wybranego sąsiada bieżącą komórką.

Rekurencyjna metoda dzielenia

Ilustracja dzielenia rekurencyjnego
oryginalna komora podział dwoma ścianami dziury w ścianach dalej dzielić... zakończony
krok 1
krok 2
krok 3
krok 4
krok 5

Labirynty można tworzyć za pomocą dzielenia rekurencyjnego , algorytmu, który działa w następujący sposób: Rozpocznij od przestrzeni labiryntu bez ścian. Nazwij to komorą. Podziel komorę losowo ustawioną ścianą (lub wieloma ścianami), gdzie każda ściana zawiera w sobie losowo rozmieszczony otwór przelotowy. Następnie rekurencyjnie powtarzaj proces na komorach podrzędnych, aż wszystkie komory osiągną minimalny rozmiar. Ta metoda skutkuje labiryntami z długimi prostymi ścianami przecinającymi ich przestrzeń, dzięki czemu łatwiej jest zobaczyć, których obszarów należy unikać.

Na przykład w labiryncie prostokątnym zbuduj w przypadkowych punktach dwie ściany, które są do siebie prostopadłe. Te dwie ściany dzielą dużą komorę na cztery mniejsze komory oddzielone czterema ścianami. Wybierz losowo trzy z czterech ścian i otwórz otwór o szerokości jednej komórki w losowym punkcie w każdej z trzech. Kontynuuj w ten sposób rekurencyjnie, aż każda komora będzie miała szerokość jednej komórki w jednym z dwóch kierunków.

Proste algorytmy

Wersja 3D algorytmu Prim. Pionowe warstwy są oznaczone od 1 do 4 od dołu do góry. Schody w górę są oznaczone „/”; schody w dół za pomocą „\”, a schody w górę iw dół za pomocą „x”. Kod źródłowy jest dołączony do opisu obrazu.

Istnieją inne algorytmy, które wymagają tylko tyle pamięci, aby zapisać jedną linię labiryntu 2D lub jedną płaszczyznę labiryntu 3D. Algorytm Ellera zapobiega pętlom, zapamiętując, które komórki w bieżącym wierszu są połączone przez komórki w poprzednich wierszach, i nigdy nie usuwa ścian między dowolnymi dwoma komórkami już połączonymi. Algorytm Sidewinder rozpoczyna się od otwartego przejścia wzdłuż całego górnego rzędu, a kolejne rzędy składają się z krótszych przejść poziomych z jednym połączeniem z przejściem powyżej. Algorytm Sidewindera jest trywialny do rozwiązania od dołu do góry, ponieważ nie ma ślepych zaułków skierowanych w górę. Biorąc pod uwagę szerokość początkową, oba algorytmy tworzą doskonałe labirynty o nieograniczonej wysokości.

Większość algorytmów generowania labiryntu wymaga utrzymywania relacji między komórkami w jego obrębie, aby zapewnić, że wynik końcowy będzie możliwy do rozwiązania. Prawidłowe, po prostu połączone labirynty można jednak wygenerować, skupiając się na każdej komórce niezależnie. Labirynt drzewa binarnego to standardowy labirynt ortogonalny, w którym każda komórka zawsze ma przejście prowadzące w górę lub w lewo, ale nigdy w obu. Aby utworzyć labirynt drzewa binarnego, dla każdej komórki rzuć monetą, aby zdecydować, czy dodać przejście prowadzące w górę, czy w lewo. Zawsze wybieraj ten sam kierunek dla komórek na granicy, a wynikiem końcowym będzie poprawny, po prostu połączony labirynt, który wygląda jak drzewo binarne , z lewym górnym rogiem jako korzeniem. Podobnie jak w przypadku Sidewinder, labirynt drzewa binarnego nie ma ślepych zaułków w kierunkach odchylenia.

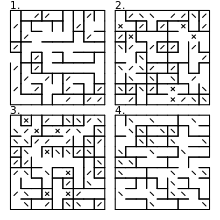
Labirynt wygenerowany w Commodore 64 BASIC przy użyciu kodu 10 PRINT CHR$(205.5+RND(1)); : PRZEJDŹ DO 10

Pokrewną formą rzucania monetą dla każdej komórki jest utworzenie obrazu przy użyciu losowej kombinacji ukośników i ukośników odwrotnych. To nie generuje prawidłowego, po prostu połączonego labiryntu, ale raczej wybór zamkniętych pętli i jednokierunkowych przejść. Instrukcja obsługi Commodore 64 przedstawia program BASIC wykorzystujący ten algorytm, zamiast tego używając znaków graficznych ukośnych linii PETSCII , aby uzyskać gładszy wygląd graficzny.

Algorytmy automatów komórkowych

Niektóre typy automatów komórkowych mogą być używane do generowania labiryntów. Dwa dobrze znane automaty komórkowe, Maze i Mazectric, mają łańcuchy reguł B3/S12345 i B3/S1234. W pierwszym oznacza to, że komórki przeżywają z pokolenia na pokolenie, jeśli mają co najmniej jednego, a co najwyżej pięciu sąsiadów . W tym drugim przypadku oznacza to, że komórki przeżywają, jeśli mają od jednego do czterech sąsiadów. Jeśli komórka ma dokładnie trzech sąsiadów, rodzi się. Jest podobny do Gry w życie Conwaya we wzorcach, które nie mają żywej komórki sąsiadującej z 1, 4 lub 5 innymi żywymi komórkami w dowolnym pokoleniu, będą zachowywać się identycznie. Jednak w przypadku dużych wzorców zachowuje się zupełnie inaczej niż Life.

Aby uzyskać losowy wzór początkowy, te generujące labirynt automaty komórkowe ewoluują w złożone labirynty z dobrze zdefiniowanymi ścianami wyznaczającymi korytarze. Mazecetric, który ma regułę B3/S1234, ma tendencję do generowania dłuższych i prostszych korytarzy w porównaniu z Maze, z regułą B3/S12345. Ponieważ te reguły automatów komórkowych są deterministyczne , każdy wygenerowany labirynt jest jednoznacznie określony przez losowy wzór początkowy. Jest to istotna wada, ponieważ labirynty wydają się być stosunkowo przewidywalne.

Podobnie jak niektóre z opisanych powyżej metod opartych na teorii grafów, te automaty komórkowe zazwyczaj generują labirynty z pojedynczego wzorca początkowego; stąd zwykle stosunkowo łatwo będzie znaleźć drogę do komórki początkowej, ale trudniej znaleźć drogę gdziekolwiek indziej.

Zobacz też

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Maze_generation_algorithm&oldid=1142025506 ”