Algorytm liniowy Bresenhama

Algorytm linii Bresenhama to algorytm rysowania linii , który określa punkty n -wymiarowego rastra , które należy wybrać, aby utworzyć bliskie przybliżenie linii prostej między dwoma punktami . Jest powszechnie używany do rysowania prymitywów liniowych w obrazie bitmapowym (np. na ekranie komputera ), ponieważ wykorzystuje tylko dodawanie, odejmowanie i przesuwanie bitów , z których wszystkie są bardzo tanimi operacjami w powszechnie używanych zestawach instrukcji komputerowych , takich jak x86_64 . Jest to przyrostowy algorytm błędu i jeden z najwcześniejszych algorytmów opracowanych w dziedzinie grafiki komputerowej . Do rysowania okręgów można zastosować rozszerzenie oryginalnego algorytmu .

Chociaż algorytmy takie jak algorytm Wu są również często używane w nowoczesnej grafice komputerowej, ponieważ mogą obsługiwać antyaliasing , algorytm liniowy Bresenhama jest nadal ważny ze względu na swoją szybkość i prostotę. Algorytm jest używany w sprzęcie takim jak plotery oraz w układach graficznych nowoczesnych kart graficznych . Można go również znaleźć w wielu bibliotekach graficznych oprogramowania . Ponieważ algorytm jest bardzo prosty, często jest implementowany w oprogramowaniu układowym lub sprzęcie graficznym nowoczesnych kart graficznych .

Etykieta „Bresenham” jest dziś używana dla rodziny algorytmów rozszerzających lub modyfikujących oryginalny algorytm Bresenhama.

Historia

Algorytm liniowy Bresenhama nosi imię Jacka Eltona Bresenhama , który opracował go w 1962 roku w IBM . W 2001 roku Bresenham napisał:

Pracowałem w laboratorium obliczeniowym w laboratorium rozwojowym IBM w San Jose. Ploter Calcomp został podłączony do IBM 1401 za pośrednictwem konsoli maszyny do pisania 1407. [Algorytm] był używany w produkcji latem 1962 roku, prawdopodobnie miesiąc wcześniej. Programy w tamtych czasach były swobodnie wymieniane między korporacjami, więc Calcomp (Jim Newland i Calvin Hefte) miał kopie. Kiedy jesienią 1962 roku wróciłem do Stanford, umieściłem kopię w bibliotece Stanford Comp Center. Opis procedury rysowania linii został przyjęty do prezentacji na ACM w 1963 r. w Denver w stanie Kolorado. Był to rok, w którym nie publikowano żadnych obrad, a jedynie program prelegentów i tematy w numerze Komunikatów ACM. Osoba z IBM Systems Journal zapytała mnie po mojej prezentacji, czy mogliby opublikować artykuł. Z radością się zgodziłem i wydrukowali go w 1965 roku.

Algorytm Bresenhama został rozszerzony, aby tworzyć okręgi, elipsy, sześcienne i kwadratowe krzywe Beziera, a także ich natywne wersje z wygładzaniem.

metoda

Ilustracja wyniku algorytmu liniowego Bresenhama. (0,0) znajduje się w lewym górnym rogu siatki, (1,1) znajduje się na lewym górnym końcu linii, a (11, 5) na prawym dolnym końcu linii.

Zastosowane zostaną następujące konwencje:

• lewy górny róg to (0,0) takie, że współrzędne piksela zwiększają się w prawo iw dół (np. piksel w punkcie (7,4) znajduje się bezpośrednio nad pikselem w punkcie (7,5)), oraz
• centra pikseli mają współrzędne całkowite.

Punkty końcowe linii to piksele w ${\ Displaystyle (x_ {0}, y_ {0})}$ i ${\ Displaystyle (x_ {1}, y_ {1} )}$ , gdzie pierwszą współrzędną pary jest kolumna, a drugą wiersz.

Algorytm zostanie początkowo przedstawiony tylko dla $} \ leq y_ {1}}$ , segment schodzi w dół iw prawo ( y ${0}}$$y_$$y_ {1} -y_ {0}}$$Displaystyle$ rzut poziomy jest dłuższy niż rzut pionowy (linia ma nachylenie dodatnie mniejsze niż 1). W tym oktancie dla każdej kolumny x między a $x_$${1}}$ jest dokładnie jeden wiersz y (obliczony przez algorytm) zawierający piksel linii, podczas każdy wiersz między $i$ może $.$ zrastrowanych

Algorytm Bresenhama wybiera liczbę całkowitą y odpowiadającą środkowi piksela , który jest najbliższy idealnemu (ułamkowi) y dla tego samego x ; na kolejnych słupach y może pozostać takie samo lub wzrosnąć o 1. Ogólne równanie prostej przechodzącej przez punkty końcowe ma postać:

${\ Displaystyle {\ Frac {y-y_ {0}} {y_ {1} -y_ {0}}} = {\ Frac {x-x_ { 0}}{x_{1}-x_{0}}}}$ .

Ponieważ znamy kolumnę x , wiersz piksela y , otrzymujemy zaokrąglając tę ​​wielkość do najbliższej liczby całkowitej:

${\ Displaystyle y = {\ Frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} (x -x_{0})+y_{0}}$ .

Nachylenie $_$ _ $a$ idealne y dla kolejnych wartości całkowitych x można obliczyć, zaczynając od i wielokrotnie dodając nachylenie.

W praktyce algorytm nie śledzi współrzędnej y, która zwiększa się o m = ∆y/∆x za każdym razem, gdy x zwiększa się o jeden; utrzymuje błąd związany na każdym etapie, który reprezentuje ujemną odległość od (a) punktu, w którym linia wychodzi z piksela do (b) górnej krawędzi piksela. $środka$ na (ze względu na piksela) i jest zwiększana o m za każdym razem, gdy x jest zwiększana o jeden. Jeśli błąd stanie się większy niż 0,5 , wiemy, że linia przesunęła się w górę o jeden piksel i że musimy zwiększyć naszą współrzędną y i ponownie dostosować błąd, aby reprezentował odległość od góry nowego piksela - co odbywa się poprzez odjęcie jednego od błąd.

Pochodzenie

Aby wyprowadzić algorytm Bresenhama, należy wykonać dwa kroki. Pierwszym krokiem jest przekształcenie równania linii z typowej postaci przecięcia z nachyleniem w coś innego; a następnie używając tego nowego równania do narysowania linii opartej na idei kumulacji błędów.

Równanie liniowe

y=f(x)=0,5x+1 lub f(x,y)=x-2y+2

Półpłaszczyzny dodatnie i ujemne

Forma przecięcia z nachyleniem linii jest zapisywana jako

${\ Displaystyle y = f (x) = mx + b}$

gdzie m to nachylenie, a b to punkt przecięcia z osią y. Ponieważ jest to funkcja tylko $.$ nie może reprezentować linii pionowej Dlatego przydatne byłoby zapisanie tego równania jako funkcji zarówno , $i$ y $aby$ móc rysować linie pod dowolnym kątem. $lub$ nachylenie ) linii można określić jako „wzrost nad Następnie, stosując manipulację algebraiczną,

${\ Displaystyle {\ rozpocząć {wyrównane} y & = mx + b \\ y & = {\ Frac {(\ Delta y)} {(\ Delta x)}} x + b \\ (\ Delta x) y&=(\Delta y)x+(\Delta x)b\\0&=(\Delta y)x-(\Delta x)y+(\Delta x)b\end{wyrównane}}}$

Niech to ostatnie równanie będzie funkcją i $displaystyle$$y}$ , można je zapisać jako x {\ displaystyle x

${\ Displaystyle f (x, y): = Ax + By + C = 0}$

gdzie są stałe

• ${\ Displaystyle A = \ delta y = y_ {1} -y_ {0}}$
• ${\ Displaystyle B = - \ Delta x = - (x_ {1} -x_ {0})}$
• ${\ Displaystyle C = (\ Delta x) b = x_ {1} y_ {0} -x_ {0} y_ {1}}$

Linia jest następnie definiowana dla niektórych stałych A, B i C w dowolnym miejscu ${\ displaystyle f (x, y) = 0}$ . Oznacza to, $y) \ neq 0$ dla dowolnego na linii $Displaystyle f$ . Ta $całkowitymi$$,$ jeśli i są liczbami , ponieważ stałe A, B i C są zdefiniowane jako liczby całkowite

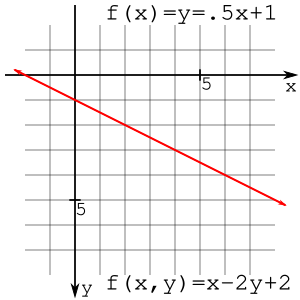
Na przykład linia ${\ Displaystyle y = {\ Frac {1} {2}} x + 1}$ to można to zapisać jako ${\ displaystyle f (x, y) = x-2y + 2}$ . Punkt (2,2) leży na prostej

${\ Displaystyle f (2,2) = x-2y + 2 = (2) -2(2)+2=2-4+2=0}$

a punkt (2,3) nie leży na prostej

${\ Displaystyle f (2,3) = (2) -2 (3) + 2 = 2-6 +2=-2}$

i nie jest to punkt (2,1)

${\ Displaystyle f (2,1) = (2) -2 (1) + 2 = 2-2 + 2=2}$

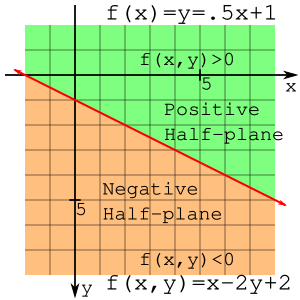
Zauważ, że punkty (2,1) i (2,3) znajdują się po przeciwnych stronach prostej, a f(x,y) ma wartość dodatnią lub ujemną. Linia dzieli płaszczyznę na połowy, a półpłaszczyznę, która ma ujemną f(x,y) można nazwać ujemną półpłaszczyzną, a drugą połowę można nazwać półpłaszczyzną dodatnią. Ta obserwacja jest bardzo ważna w dalszej części wyprowadzenia.

Algorytm

Oczywiście punkt początkowy znajduje się na linii

${\ Displaystyle f (x_ {0}, y_ {0}) = 0}$

tylko dlatego, że linia jest zdefiniowana tak, aby zaczynała się i kończyła na współrzędnych całkowitych (chociaż całkowicie rozsądne jest narysowanie linii z niecałkowitymi punktami końcowymi).

Punkt kandydujący (2,2) na niebiesko i dwa punkty kandydujące na zielono (3,2) i (3,3)

Mając na uwadze, że nachylenie wynosi co najwyżej $,$ się teraz problem, czy następny punkt powinien znajdować się w punkcie ${\ Displaystyle (x_ {0} + 1, y_ { 0})}$ lub ${\ Displaystyle (x_ {0} + 1, y_ {0} + 1)}$ . Być może intuicyjnie, punkt powinien być wybrany na podstawie tego, który jest bliżej linii w ${\ displaystyle x_ {0} + 1}$ . Jeśli jest bliżej pierwszego, uwzględnij pierwszy punkt na linii, jeśli ten drugi, to drugi. Aby odpowiedzieć na to pytanie, oblicz funkcję liniową w punkcie środkowym między tymi dwoma punktami:

${\ Displaystyle f (x_ {0} + 1, y_ {0} + {\ tfrac {1} {2}})}$

Jeśli wartość tego jest dodatnia, to idealna linia znajduje się poniżej punktu środkowego i bliżej punktu kandydującego ${\ Displaystyle (x_ {0} + 1, y_ {0} + 1)}$ ; w efekcie współrzędna y uległa przesunięciu. W przeciwnym razie idealna linia przechodzi przez punkt środkowy lub powyżej, a współrzędna y nie uległa przesunięciu; w tym przypadku wybierz punkt ${\ Displaystyle (x_ {0} + 1, y_ {0})}$ . Wartość funkcji liniowej w tym punkcie środkowym jest jedynym wyznacznikiem, który punkt należy wybrać.

Sąsiednie zdjęcie pokazuje niebieski punkt (2,2) wybrany na linię z dwoma punktami kandydującymi na zielono (3,2) i (3,3). Czarny punkt (3, 2,5) to punkt środkowy między dwoma kandydującymi punktami.

Algorytm dla arytmetyki liczb całkowitych

Alternatywnie, zamiast obliczania f(x,y) w punktach środkowych można zastosować różnicę między punktami. Ta alternatywna metoda pozwala na arytmetykę wyłącznie na liczbach całkowitych, która jest generalnie szybsza niż arytmetyka zmiennoprzecinkowa. Aby wyprowadzić metodę alternatywną, zdefiniuj różnicę w następujący sposób:

${\ Displaystyle D = f (x_ {0} + 1, y_ {0} + {\ tfrac {1} {2}}) -f(x_{0},y_{0})}$

W przypadku pierwszej decyzji to sformułowanie jest równoważne metodzie punktu środkowego, ponieważ w punkcie początkowym ${\ displaystyle f (x_ {0}, y_ {0}) = 0} .$ Upraszczając to wyrażenie, otrzymujemy:

${\ Displaystyle {\ rozpocząć {tablica} {rclcl} D & = & \ lewo [A (x_ {0} + 1) + B \ left(y_{0}+{\frac {1}{2}}\right)+C\right]&-&\left[Ax_{0}+By_{0}+C\right]\\&=& \left[Ax_{0}+By_{0}+C+A+{\frac {1}{2}}B\right]&-&\left[Ax_{0}+By_{0}+C\right] \\&=&A+{\frac {1}{2}}B=\Delta y-{\frac {1}{2}}\Delta x\end{tablica}}}$

${$ jak w przypadku metody punktu środkowego, jeśli to wybierz , razie wybierz $D$${\ Displaystyle (x_ {0} + 1, y_ {0})}$ .

Jeśli $_$ _

${\ Displaystyle {\ rozpocząć {tablica} {lclcl} \ Delta D & = & f (x_ {0}+2,y_{0}+{\tfrac {1}{2}})-f(x_{0}+1,y_{0}+{\tfrac {1}{2}})&= &A&=&\Delta y\\\koniec{tablica}}}$

Jeśli $_$ _

${\ Displaystyle {\ rozpocząć {tablica} {lclcl} \ Delta D&=&f(x_{0}+2,y_{0}+{\tfrac {3}{2}})-f(x_{0}+1,y_{0}+{\tfrac {1}{2 }})&=&A+B&=&\Delta y-\Delta x\end{tablica}}}$

$x_{0}+2,y_{0})}$ nowe re jest dodatnie, $2$ w przeciwnym $Displaystyle$ . Decyzję tę można uogólnić, sumując błąd w każdym kolejnym punkcie.

Wykreślanie linii od (0,1) do (6,4) przedstawiającej wykres linii siatki i pikseli

Całe wyprowadzenie algorytmu zostało zakończone. Jednym z problemów z wydajnością jest współczynnik 1/2 początkowej wartości D. Ponieważ wszystko to dotyczy znaku skumulowanej różnicy, wszystko można pomnożyć przez 2 bez żadnych konsekwencji.

Powoduje to algorytm, który używa tylko arytmetyki liczb całkowitych.

 plotLine(x0, y0, x1, y1) dx = x1 - x0 dy = y1 - y0 D = 2*dy - dx y = y0  dla  x od x0 do x1 wykres(x, y)  if  D > 0 y = y + 1 D = D - 2*dx  koniec, jeśli  D = D + 2*dy 

$6,4$ algorytmu do dx=6 i dy=3:

 D=2*3-6=0 Pętla od 0 do 6 * x=0:  wykres(0, 1)  , D≤0: D=0+6=6 * x=1:  wykres(1, 1)  , D >0: D=6-12=-6, y=1+1=2, D=-6+6=0 * x=2:  wykres(2, 2)  , D≤0: D=0+6= 6 * x=3:  wykres(3, 2)  , D>0: D=6-12=-6, y=2+1=3, D=-6+6=0 * x=4: wykres(  4 , 3)  , D≤0: D=0+6=6 * x=5:  wykres(5, 3)  , D>0: D=6-12=-6, y=3+1=4, D= -6+6=0 * x=6:  wykres(6, 4)  , D≤0: D=0+6=6 

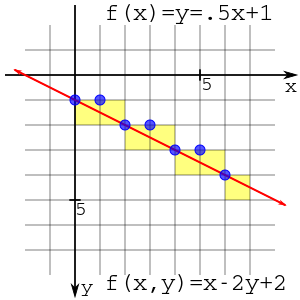
Wynik tego wykresu jest pokazany po prawej stronie. Wykreślenie można obejrzeć, wykreślając na przecięciu linii (niebieskie kółka) lub wypełniając pola pikseli (żółte kwadraty). Niezależnie od tego spisek jest ten sam.

Wszystkie przypadki

Jednak, jak wspomniano powyżej, działa to tylko dla oktanta zero, czyli linii rozpoczynających się w początku z nachyleniem między 0 a 1, gdzie x zwiększa się dokładnie o 1 na iterację, a y zwiększa się o 0 lub 1.

Algorytm można rozszerzyć, aby obejmował nachylenia od 0 do -1, sprawdzając, czy y należy zwiększyć, czy zmniejszyć (tj. dy < 0)

 plotLineLow(x0, y0, x1, y1) dx = x1 - x0 dy = y1 - y0 yi = 1  jeśli  dy < 0 yi = -1 dy = -dy  koniec jeśli  D = (2 * dy) - dx y = y0  dla  x od x0 do x1 wykres(x, y)  jeśli  D > 0 y = y + yi D = D + (2 * (dy - dx))  w przeciwnym razie  D = D + 2*dy  koniec, jeśli 

Zamieniając osie x i y, implementację dla dodatnich lub ujemnych stromych zboczy można zapisać jako

 plotLineHigh(x0, y0, x1, y1) dx = x1 - x0 dy = y1 - y0 xi = 1  jeśli  dx < 0 xi = -1 dx = -dx  koniec jeśli  D = (2 * dx) - dy x = x0  dla  y od y0 do y1 wykres(x, y)  jeśli  D > 0 x = x + xi D = D + (2 * (dx - dy))  w przeciwnym razie  D = D + 2*dx  koniec, jeśli 

Kompletne rozwiązanie wymagałoby wykrycia, czy x1 > x0 lub y1 > y0 i odwrócenia współrzędnych wejściowych przed rysowaniem, a zatem

    
        
     plotLine(x0, y0, x1, y1)  if  abs(y1 - y0) < abs(x1 - x0)  if  x0 > x1 plotLineLow(x1, y1, x0, y0)  else  plotLineLow(x0, y0, x1, y1)  end if  else  if  y0 > y1 plotLineHigh(x1, y1, x0, y0)  else  plotLineHigh(x0, y0, x1, y1)  koniec if  koniec if 

W implementacjach niskiego poziomu, które uzyskują bezpośredni dostęp do pamięci wideo, typowe byłoby osobne traktowanie specjalnych przypadków linii pionowych i poziomych, ponieważ można je wysoce zoptymalizować.

Niektóre wersje wykorzystują zasady Bresenhama dotyczące błędu inkrementalnego liczb całkowitych, aby wykonać wszystkie rysowania linii oktanowych, równoważąc błąd dodatni i ujemny między współrzędnymi x i y. Pamiętaj, że zamówienie niekoniecznie jest gwarantowane; innymi słowy, linię można poprowadzić od (x0, y0) do (x1, y1) lub od (x1, y1) do (x0, y0).

        
     wykresLinia(x0, y0, x1, y1) dx = abs(x1 - x0) sx = x0 < x1 ? 1 : -1 dy = -abs(y1 - y0) sy = y0 < y1 ?  1 : -1 błąd = dx + dy   podczas gdy  prawda wykres(x0, y0)  if  x0 == x1 && y0 == y1  przerwa  e2 = 2 * błąd  jeśli  e2 >= dy  jeśli  x0 == x1  przerwa  błąd = błąd + dy x0 = x0 + sx  koniec jeśli  jeśli  e2 <= dx  jeśli  y0 == y1 błąd   przerwania  = błąd + dx y0 = y0 + sy  koniec jeśli  koniec podczas 

Podobne algorytmy

Algorytm Bresenhama można interpretować jako nieco zmodyfikowany cyfrowy analizator różnicowy (wykorzystujący 0,5 jako próg błędu zamiast 0, co jest wymagane do rasteryzacji wielokątów bez nakładania się).

Zasada stosowania błędu przyrostowego zamiast operacji dzielenia ma inne zastosowania w grafice. Technikę tę można wykorzystać do obliczenia współrzędnych U, V podczas skanowania rastrowego wielokątów z odwzorowaniem tekstury. Silniki wokseli , które można znaleźć w niektórych grach na komputery PC, również wykorzystywały tę zasadę.

Bresenham opublikował również algorytm obliczeniowy Run-Slice (w przeciwieństwie do Run-Length). Ta metoda została przedstawiona w wielu patentach amerykańskich:

5815163		Sposób i aparatura do rysowania przekrojów linii podczas obliczeń
5 740 345		Sposób i urządzenie do wyświetlania komputerowych danych graficznych przechowywanych w skompresowanym formacie z wydajnym systemem indeksowania kolorów
5 657 435		Uruchom mechanizm rysowania linii przekroju z możliwością skalowania nieliniowego
5 627 957		Uruchom mechanizm rysowania linii przekroju z ulepszonymi możliwościami przetwarzania
5 627 956		Uruchom silnik rysowania linii plasterków z możliwością rozciągania
5 617 524		Uruchom silnik rysowania linii plasterków z możliwością cieniowania
5 611 029		Uruchom mechanizm rysowania linii przekroju z możliwością cieniowania nieliniowego
5 604 852		Sposób i urządzenie do wyświetlania krzywej parametrycznej na wyświetlaczu wideo
5 600 769		Uruchom silnik rysowania linii plasterków z ulepszonymi technikami przycinania

Rozszerzenie algorytmu obsługujące grube linie zostało stworzone przez Alana Murphy'ego z IBM.

Zobacz też

• Cyfrowy analizator różnicowy (algorytm graficzny) , prosta i ogólna metoda rasteryzacji linii i trójkątów
• Algorytm linii Xiaolin Wu , podobnie szybka metoda rysowania linii z antyaliasingiem
• Algorytm okręgu punktu środkowego , podobny algorytm do rysowania okręgów

Notatki

• Bresenham, JE (1965). „Algorytm komputerowego sterowania ploterem cyfrowym” (PDF) . Dziennik systemów IBM . 4 (1): 25–30. doi : 10.1147/sj.41.0025 . Zarchiwizowane od oryginału (PDF) w dniu 28 maja 2008 r.
• „Algorytm rysowania linii Bresenham” autorstwa Colina Flanagana
•   Abrasz, Michael (1997). Czarna księga programowania grafiki Michaela Abrasha . Albany, NY: Coriolis. s. 654–678 . ISBN 978-1-57610-174-2 . Bardzo zoptymalizowana wersja algorytmu w C i asemblerze do użytku w grach wideo z pełnymi szczegółami jego wewnętrznego działania
• Zingl, Alois (2012). „Algorytm rasteryzacji do rysowania krzywych” (PDF) . , Piękno algorytmów Bresenhama

Dalsza lektura

•   Teza Patricka-Gillesa Maillota rozszerzenie algorytmu rysowania linii Bresenham w celu usunięcia ukrytych linii 3D; opublikowane również w materiałach MICAD '87 dotyczących CAD/CAM i grafiki komputerowej, strona 591 - ISBN 2-86601-084-1 .
• Pogrubienie linii przez modyfikację algorytmu Bresenhama , AS Murphy, IBM Technical Disclosure Bulletin, tom. 20, nr 12, maj 1978.

zamiast [co] do rozszerzenia okręgu użyj: Technical Report 1964 Jan-27 -11- Circle Algorithm TR-02-286 IBM San Jose Lab or A Linear Algorithm for Incremental Digital Display of Circular Arcs, luty 1977 Communications of the ACM 20(2 ):100-106 DOI:10.1145/359423.359432

Linki zewnętrzne

• Michael Abrash's Graphics Programming Black Book Special Edition: Rozdział 35: Bresenham jest szybki, a szybki jest dobry
• Algorytm rysowania linii Bresenham autorstwa Colina Flanagana
• Strona National Institute of Standards and Technology poświęcona algorytmowi Bresenhama
• Informacje o ploterze przyrostowym Calcomp 563
• Algorytm Bresenhama w kilku językach programowania
• The Beauty of Bresenham's Algorithm - Prosta implementacja do kreślenia linii, okręgów, elips i krzywych Béziera