Algorytm odwrotnego usuwania

Algorytm odwrotnego usuwania to algorytm w teorii grafów używany do uzyskania minimalnego drzewa rozpinającego z danego połączonego grafu ważonego krawędziami . Po raz pierwszy pojawił się w Kruskalu (1956) , ale nie należy go mylić z algorytmem Kruskala , który pojawia się w tym samym artykule. Jeśli graf jest rozłączony, ten algorytm znajdzie minimalne drzewo rozpinające dla każdej odłączonej części grafu. Zbiór tych minimalnych drzew rozpinających nazywany jest minimalnym lasem rozpinającym, który zawiera każdy wierzchołek grafu.

Algorytm ten jest algorytmem zachłannym , wybierającym najlepszy wybór w każdej sytuacji. Jest to odwrotność algorytmu Kruskala , który jest kolejnym zachłannym algorytmem znajdowania minimalnego drzewa rozpinającego. Algorytm Kruskala zaczyna się od pustego wykresu i dodaje krawędzie, podczas gdy algorytm Reverse-Delete zaczyna od oryginalnego wykresu i usuwa z niego krawędzie. Algorytm działa w następujący sposób:

  • Zacznij od wykresu G, który zawiera listę krawędzi E.
  • Przejdź przez E w malejącej kolejności wag krawędzi.
  • Dla każdej krawędzi sprawdź, czy usunięcie krawędzi spowoduje dalsze rozłączenie wykresu.
  • Wykonaj każde usunięcie, które nie prowadzi do dodatkowego rozłączenia.

Pseudo kod 

       
                
                 funkcja  ReverseDelete(edges[]  E  )  to  sortowanie  E  w kolejności malejącej Zdefiniuj indeks  i  ← 0  while  i  <  rozmiar  (  E  )  do  Zdefiniuj  krawędź  ←  E  [  i  ]  usuń  E  [  i  ]  jeśli  wykres nie jest połączony,  to  E  [  i  ] ←  krawędź  ja  ←  i  + 1  powrót  krawędzie[]  E

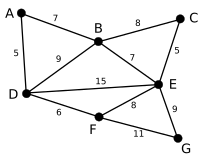
Na powyższym grafie jest zbiorem krawędzi E , z których każda zawiera wagę i połączone wierzchołki v1 i v2 .

Przykład

W poniższym przykładzie zielone krawędzie są oceniane przez algorytm, a czerwone krawędzie są usuwane.

Reverse Delete 0.svg To jest nasz autorski wykres. Liczby przy krawędziach oznaczają wagę krawędzi.
Reverse Delete 1.svg Algorytm rozpocznie się od maksymalnej ważonej krawędzi, którą w tym przypadku jest DE z wagą krawędzi równą 15. Ponieważ usunięcie krawędzi DE nie powoduje dalszego rozłączenia wykresu, jest ona usuwana.
Reverse Delete 2.svg Następną największą krawędzią jest FG , więc algorytm sprawdzi, czy usunięcie tej krawędzi jeszcze bardziej rozłączy wykres. Ponieważ usunięcie krawędzi nie spowoduje dalszego rozłączenia wykresu, krawędź jest następnie usuwana.
Reverse Delete 3.svg Następną największą krawędzią jest krawędź BD , więc algorytm sprawdzi tę krawędź i usunie ją.
Reverse Delete 4.svg Następną krawędzią do sprawdzenia jest krawędź EG , która nie zostanie usunięta, ponieważ odłączyłaby węzeł G od grafu. Dlatego następną krawędzią do usunięcia jest krawędź BC .
Reverse Delete 5.svg Następną największą krawędzią jest krawędź EF , więc algorytm sprawdzi tę krawędź i usunie ją.
Reverse Delete 6.svg Algorytm przeszuka następnie pozostałe krawędzie i nie znajdzie kolejnej krawędzi do usunięcia; dlatego jest to końcowy wykres zwrócony przez algorytm.

Czas działania

Można pokazać, że algorytm działa w czasie O ( E log V (log log V ) 3 ) (używając notacji dużego O ), gdzie E to liczba krawędzi, a V to liczba wierzchołków. Ta granica jest osiągana w następujący sposób:

  • Sortowanie krawędzi według wagi za pomocą sortowania porównawczego zajmuje O ( E log E ) czasu, który można uprościć do O ( E log V ) wykorzystując fakt, że największym E może być V 2 .
  • Istnieje E iteracji pętli.
  • Usuwanie krawędzi, sprawdzanie łączności wynikowego wykresu i (jeśli jest odłączone) ponowne wstawianie krawędzi można wykonać w O (log V (log log V ) 3 ) czasu na operację ( Thorup 2000 ).

Dowód poprawności

Zaleca się najpierw przeczytać dowód algorytmu Kruskala .

Dowód składa się z dwóch części. Po pierwsze, udowodniono, że krawędzie, które pozostają po zastosowaniu algorytmu, tworzą drzewo rozpinające. Po drugie, udowodniono, że drzewo rozpinające ma minimalną wagę.

Drzewo rozpinające

Pozostały podwykres (g) wygenerowany przez algorytm nie jest odłączony, ponieważ algorytm sprawdza to w wierszu 7. Wynikowy podwykres nie może zawierać cyklu, ponieważ jeśli tak, to poruszając się po krawędziach napotkalibyśmy maksymalną krawędź w cyklu i usunęlibyśmy tę krawędź. Zatem g musi być drzewem rozpinającym grafu głównego G.

Minimalizm

Pokazujemy, że następujące twierdzenie P jest prawdziwe przez indukcję: Jeśli F jest zbiorem krawędzi pozostałych na końcu pętli while, to istnieje pewne minimalne drzewo rozpinające, którego (jego krawędzie) są podzbiorem F .

  1. Oczywiście P trzyma się przed początkiem pętli while. ponieważ ważony spójny graf zawsze ma minimalne drzewo rozpinające i ponieważ F zawiera wszystkie krawędzie grafu, to to minimalne drzewo rozpinające musi być podzbiorem F.
  2. Załóżmy teraz, że P jest prawdziwe dla pewnego niekońcowego zbioru krawędzi F i niech T będzie minimalnym drzewem rozpinającym zawartym w F. musimy pokazać, że po usunięciu krawędzi e w algorytmie istnieje jakieś (być może inne) drzewo rozpinające T', które jest podzbiorem F.
    1. jeśli następna usunięta krawędź e nie należy do T, to T=T' jest podzbiorem F i posiada P. .
    2. w przeciwnym razie, jeśli e należy do T: najpierw zauważ, że algorytm usuwa tylko te krawędzie, które nie powodują rozłączenia w F. więc e nie powoduje rozłączenia. Ale usunięcie e powoduje rozłączenie w drzewie T (ponieważ jest ono członkiem T). załóżmy, że e dzieli T na podgrafy t1 i t2. Skoro cały graf jest spójny po usunięciu e, to między t1 i t2 musi istnieć ścieżka (inna niż e), więc w F (przed usunięciem e) musi istnieć cykl C. teraz musimy mieć kolejną krawędź w tym cyklu (nazwijmy ją f), która nie jest w T, ale jest w F (ponieważ gdyby wszystkie krawędzie cyklu były w drzewie T, to nie byłoby już drzewem). teraz twierdzimy, że T' = T - e + f jest minimalnym drzewem rozpinającym, które jest podzbiorem F.
    3. najpierw udowodnimy, że T' jest drzewem rozpinającym . wiemy, że usuwając krawędź w drzewie i dodając kolejną krawędź, która nie powoduje cyklu, otrzymujemy kolejne drzewo z tymi samymi wierzchołkami. skoro T było drzewem rozpinającym, to T' też musi być drzewem rozpinającym . ponieważ dodanie „ f ” nie powoduje żadnych cykli, ponieważ usunięto „e”. (zauważ, że drzewo T zawiera wszystkie wierzchołki grafu).
    4. po drugie dowodzimy, że T' jest minimalnym drzewem rozpinającym. mamy trzy przypadki dla krawędzi „e” i „f”. wt jest funkcją wagi.
      1. wt( f ) < wt ( e ) jest to niemożliwe, ponieważ powoduje to, że ciężar drzewa T' jest dokładnie mniejszy niż T . ponieważ T jest minimalnym drzewem rozpinającym, jest to po prostu niemożliwe.
      2. wt( f ) > wt ( e ) to również jest niemożliwe. od tego czasu, gdy przechodzimy przez krawędzie w malejącej kolejności wag krawędzi, musimy najpierw zobaczyć „f”. ponieważ mamy cykl C, więc usunięcie „f” nie spowodowałoby żadnego rozłączenia w F. więc algorytm usunąłby go z F wcześniej. więc „f” nie istnieje w F, co jest niemożliwe (udowodniliśmy, że f istnieje w kroku 4.
      3. więc wt(f) = wt(e) więc T' jest również minimalnym drzewem rozpinającym. więc znowu P trzyma.
  3. więc P zachodzi, gdy pętla while jest zakończona (czyli wtedy, gdy widzieliśmy wszystkie krawędzie) i udowodniliśmy, że na końcu F staje się drzewem rozpinającym i wiemy, że F ma minimalne drzewo rozpinające jako swój podzbiór. więc F musi być minimalnym drzewem rozpinającym .

Zobacz też

  • Kleinberg, Jon; Tardos, Éva (2006), Projektowanie algorytmów , Nowy Jork: Pearson Education, Inc.
  •   Kruskal, Joseph B. (1956), „O najkrótszym obejmującym poddrzewo wykresu i problem komiwojażera”, Proceedings of the American Mathematical Society , 7 (1): 48–50, doi : 10,2307/2033241 , JSTOR 2033241 .
  • Thorup, Mikkel (2000), „Niemal optymalna, w pełni dynamiczna łączność grafów”, Proc. 32. Sympozjum ACM na temat teorii informatyki , s. 343–350, doi : 10.1145/335305.335345 .
Pobrano z „ https://en.wikipedia.org/w/index.php?title=Reverse-delete_algorithm&oldid=1141998746 ”