Algorytm wyszukiwania A*

Nie mylić ze Strzelcem A* .

Klasa	Algorytm wyszukiwania
Struktura danych	Wykres
Wydajność w najgorszym przypadku	${\ Displaystyle O (| E |) = O (b ^ {d})}$
Złożoność przestrzeni w najgorszym przypadku	${\ Displaystyle O (| V |) = O (b ^ {d})}$

A* (czyt. „A-star”) to algorytm przechodzenia przez graf i przeszukiwania ścieżki , który jest używany w wielu dziedzinach informatyki ze względu na swoją kompletność, optymalizację i optymalną wydajność. Jedną $z głównych praktycznych$ jest złożoność przestrzeni ponieważ przechowuje wszystkie wygenerowane węzły Tak więc w praktycznych systemach wyznaczania tras podróży generalnie przewyższają go algorytmy, które mogą wstępnie przetwarzać wykres w celu uzyskania lepszej wydajności, a także podejścia ograniczone pamięcią; jednak A* jest nadal najlepszym rozwiązaniem w wielu przypadkach.

Peter Hart , Nils Nilsson i Bertram Raphael ze Stanford Research Institute (obecnie SRI International ) po raz pierwszy opublikowali algorytm w 1968 roku. Można go postrzegać jako rozszerzenie algorytmu Dijkstry . A* osiąga lepszą wydajność, używając heurystyki do kierowania wyszukiwaniem.

W porównaniu z algorytmem Dijkstry, algorytm A* znajduje tylko najkrótszą ścieżkę od określonego źródła do określonego celu, a nie drzewo najkrótszej ścieżki od określonego źródła do wszystkich możliwych celów. Jest to niezbędny kompromis w przypadku stosowania heurystyki ukierunkowanej na określony cel. W przypadku algorytmu Dijkstry, ponieważ generowane jest całe drzewo najkrótszej ścieżki, każdy węzeł jest celem i nie może istnieć żadna heurystyka ukierunkowana na konkretny cel.

Historia

A* został wynaleziony przez badaczy pracujących nad planowaniem ścieżki robota Shakey.

A* powstało w ramach projektu Shakey , którego celem było zbudowanie robota mobilnego potrafiącego planować własne działania. Nils Nilsson pierwotnie zaproponował użycie algorytmu Graph Traverser do planowania ścieżki Shakeya. Graph Traverser jest prowadzony przez funkcję heurystyczną h ( n ) , szacowaną odległość od węzła n do węzła docelowego: całkowicie ignoruje g ( n ) , odległość od węzła początkowego do n . Bertram Raphael zasugerował użycie sumy g ( n ) + h ( n ) . Peter Hart wynalazł pojęcia, które obecnie nazywamy dopuszczalnością i spójnością funkcji heurystycznych. A* została pierwotnie zaprojektowana do znajdowania ścieżek o najniższym koszcie, gdy koszt ścieżki jest sumą jej kosztów, ale wykazano, że A* można użyć do znalezienia optymalnych ścieżek dla dowolnego problemu spełniającego warunki algebry kosztów.

Oryginalny artykuł A* z 1968 r. zawierał twierdzenie stwierdzające, że żaden algorytm podobny do A* nie może rozszerzyć mniejszej liczby węzłów niż A*, jeśli funkcja heurystyczna jest spójna, a reguła rozstrzygania remisów A* jest odpowiednio wybrana. „Korekta” została opublikowana kilka lat później, twierdząc, że spójność nie jest wymagana, ale okazało się to fałszywe w ostatecznym badaniu optymalności A * przeprowadzonym przez Dechtera i Pearla (obecnie nazywanym optymalną wydajnością), które dało przykład A * z heurystyką, która była dopuszczalna, ale niespójna, rozszerzając arbitralnie więcej węzłów niż alternatywny algorytm podobny do A *.

Opis

Algorytm wyszukiwania ścieżki A* poruszający się po losowo wygenerowanym labiryncie

Ilustracja wyszukiwania A* w celu znalezienia ścieżki między dwoma punktami na wykresie. Od lewej do prawej, coraz częściej stosowana jest heurystyka, która preferuje punkty bliżej celu.

A* jest świadomym algorytmem wyszukiwania lub wyszukiwaniem najpierw najlepiej , co oznacza, że ​​jest sformułowane w postaci grafów ważonych : zaczynając od określonego węzła początkowego grafu, ma na celu znalezienie ścieżki do danego węzła docelowego o najmniejszym koszt (najmniejsza przebyta odległość, najkrótszy czas itp.). Robi to, utrzymując drzewo ścieżek rozpoczynających się w węźle początkowym i rozszerzając te ścieżki o jedną krawędź na raz, aż spełnione zostanie kryterium zakończenia.

W każdej iteracji swojej głównej pętli A* musi określić, którą ze swoich ścieżek rozszerzyć. Czyni to na podstawie kosztu ścieżki i szacunkowego kosztu wymaganego do przedłużenia ścieżki aż do celu. W szczególności A* wybiera ścieżkę, która minimalizuje

${\ Displaystyle f (n) = g (n) + h (n)}$

gdzie n to następny węzeł na ścieżce, g ( n ) to koszt ścieżki od węzła początkowego do n , a h ( n ) to funkcja heurystyczna , która szacuje koszt najtańszej ścieżki od n do celu. A* kończy się, gdy ścieżka, którą wybiera do przedłużenia, jest ścieżką od początku do celu lub jeśli nie ma ścieżek, które można wydłużyć. Funkcja heurystyczna jest specyficzna dla problemu. Jeśli funkcja heurystyczna jest dopuszczalna – co oznacza, że ​​nigdy nie przeszacowuje rzeczywistego kosztu dotarcia do celu – A* gwarantuje zwrócenie ścieżki o najmniejszym koszcie od początku do celu.

Typowe implementacje A* wykorzystują kolejkę priorytetową do wykonywania powtarzanego wyboru węzłów o minimalnym (szacowanym) koszcie do rozwinięcia. Ta kolejka priorytetowa jest znana jako zbiór otwarty , prążek lub granica. W każdym kroku algorytmu węzeł z najniższą f ( x ) jest usuwany z kolejki, odpowiednio aktualizowane są wartości f i g jego sąsiadów, a ci sąsiedzi są dodawani do kolejki. Algorytm jest kontynuowany, dopóki usunięty węzeł (a więc węzeł o najniższej f spośród wszystkich węzłów brzegowych) nie stanie się węzłem docelowym. Wartość f tego celu jest wtedy również kosztem najkrótszej ścieżki, ponieważ h przy celu wynosi zero w dopuszczalnej heurystyce.

Opisany dotychczas algorytm podaje nam tylko długość najkrótszej ścieżki. Aby znaleźć rzeczywistą sekwencję kroków, algorytm można łatwo zmienić, tak aby każdy węzeł na ścieżce śledził swojego poprzednika. Po uruchomieniu tego algorytmu węzeł końcowy będzie wskazywał na swojego poprzednika i tak dalej, aż poprzednik jakiegoś węzła będzie węzłem początkowym.

Na przykład podczas wyszukiwania najkrótszej trasy na mapie h ( x ) może reprezentować odległość do celu w linii prostej , ponieważ jest to fizycznie najmniejsza możliwa odległość między dowolnymi dwoma punktami. W przypadku mapy siatkowej z gry wideo użycie odległości Manhattanu lub odległości oktylowej staje się lepsze w zależności od dostępnego zestawu ruchów (4-kierunkowy lub 8-kierunkowy).

Jeśli heurystyka h spełnia dodatkowy warunek h ( x ) ≤ d ( x , y ) + h ( y ) dla każdej krawędzi ( x , y ) grafu (gdzie d oznacza długość tej krawędzi), to h nazywa się monotonne lub spójne . Przy spójnej heurystyce A* gwarantuje znalezienie optymalnej ścieżki bez przetwarzania żadnego węzła więcej niż jeden raz, a A* jest równoważne uruchomieniu algorytmu Dijkstry ze zmniejszonym kosztem d' ( x , y ) = d ( x , y ) + h ( y ) - h ( x ) .

Pseudo kod

Poniższy pseudokod opisuje algorytm:

  
      
       
          
        
     



   
    
    
    
      

    
    
        

    
           
      0

    
    
           
      

        
        
                  
           
              

        
            
            
            
                 
               
                
                  
                  
                    
                    
                    

    
      funkcja  ścieżka_rekonstrukcji  (  pochodzi z  ,  bieżąca  )  ścieżka_całkowita  :=  {bieżąca}  podczas gdy  bieżąca  w  pochodzi z  .  Klucze  :  current  :=  comeFrom  [  current  ]  total_path  .  prepend  (  current  )  return  total_path  // A* znajduje ścieżkę od początku do celu.  // h jest funkcją heurystyczną. h(n) szacuje koszt osiągnięcia celu z węzła n.   function  A_Star  (  start  ,  gol  ,  h  )  // Zbiór wykrytych węzłów, które mogą wymagać (ponownego) rozszerzenia.  // Początkowo znany jest tylko węzeł początkowy.  // Zwykle jest to implementowane jako min-heap lub kolejka priorytetowa, a nie zestaw mieszający.  openSet  :=  {start}  // Dla węzła n, cameFrom[n] jest węzłem bezpośrednio poprzedzającym go na najtańszej ścieżce od początku  // do n obecnie znanej.  cameFrom  :=  pusta  mapa  // Dla węzła n gScore[n] to koszt najtańszej obecnie znanej ścieżki od początku do n  .  gScore  :=  mapa  z  domyślną  wartością  Infinity  gScore  [  start  ]  :=  // Dla węzła n, fScore[n] := gScore[n] + h(n)  .  fScore[n] przedstawia nasze obecne najlepsze przypuszczenia,  // jak tania może być ścieżka od początku do końca, jeśli przechodzi przez n.  fScore  :=  mapa  z  domyślną  wartością  Infinity  fScore  [  start  ]  :=  h  (  start  )  podczas gdy  openSet  nie  jest  pusty // Ta operacja może wystąpić w czasie O(Log(N)   )  jeśli openSet jest stertą min lub kolejką priorytetową  current  :  =  węzeł  w  openSet  mający  najniższą  wartość  fScore  [  ]  jeśli  current  =  cel  return  reconstruct_path  (  camFrom  ,  current  )  openSet  .  Usuń  (  bieżący  )  dla  każdego  sąsiada  obecnego  // d(bieżący,sąsiad) to waga krawędzi od bieżącego do sąsiedniego  //  tentative_gScore to odległość od początku do sąsiada przez bieżący  tentative_gScore  :=  gScore  [  bieżący  ]  +  d  (  current  ,  sąsiad  )  if  tentative_gScore  <  gScore  [  sąsiad  ]  // Ta ścieżka do sąsiada jest lepsza niż jakakolwiek poprzednia. Nagraj to!   comeFrom  [  sąsiad  ]  :=  aktualny  gScore  [  sąsiad  ]  :=  tentative_gScore  fScore  [  sąsiad  ]  :=  tentative_gScore  +  h  (  sąsiad  )  jeśli  sąsiad  nie jest  w  openSet  openSet  .  add  (  sąsiad  )  // Otwarty zbiór jest pusty, ale cel nigdy nie został osiągnięty  zwraca  błąd 

Uwaga: W tym pseudokodzie, jeśli węzeł zostanie osiągnięty jedną ścieżką, usunięty z openSet, a następnie osiągnięty tańszą ścieżką, zostanie ponownie dodany do openSet. Jest to niezbędne do zagwarantowania, że ​​zwrócona ścieżka jest optymalna, jeśli funkcja heurystyczna jest dopuszczalna , ale niespójna . Jeśli heurystyka jest spójna, po usunięciu węzła z openSet ścieżka do niego jest gwarantowana jako optymalna, więc test „ tentative_gScore < gScore[neighbor] ” zawsze zakończy się niepowodzeniem, jeśli węzeł zostanie ponownie osiągnięty.

Ilustracja wyszukiwania A* w celu znalezienia ścieżki od węzła początkowego do węzła docelowego w problemie planowania ruchu robota . Puste kółka reprezentują węzły w zbiorze otwartym , czyli te, które pozostają do zbadania, a wypełnione w zbiorze zamkniętym. Kolor na każdym zamkniętym węźle wskazuje odległość od celu: im bardziej zielony, tym bliżej. Najpierw widać, jak A* porusza się po linii prostej w kierunku celu, a następnie uderzając w przeszkodę, bada alternatywne trasy przez węzły ze zbioru otwartego.

Zobacz też: Algorytm Dijkstry

Przykład

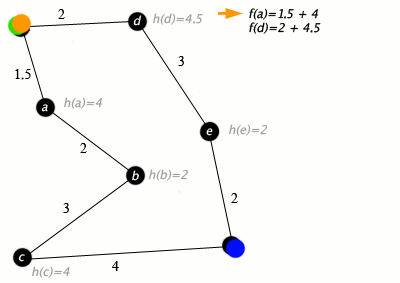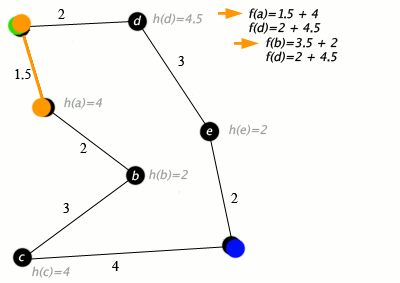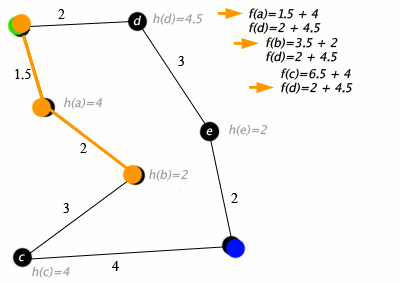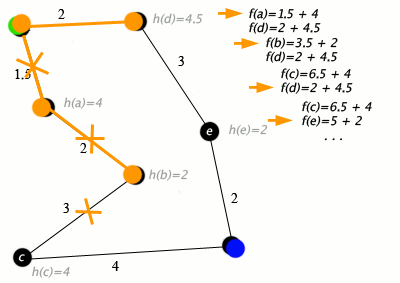
Przykład działania algorytmu A*, w którym węzły to miasta połączone drogami, a h(x) to odległość w linii prostej do punktu docelowego:

Klucz: zielony: start; niebieski: cel; pomarańczowy: odwiedzony

Algorytm A* ma również zastosowania w świecie rzeczywistym. W tym przykładzie krawędzie to linie kolejowe, a h(x) to odległość po ortodromie (najkrótsza możliwa odległość na kuli) do celu. Algorytm szuka trasy między Waszyngtonem a Los Angeles.

Szczegóły dotyczące wdrożenia

Istnieje wiele prostych optymalizacji lub szczegółów implementacji, które mogą znacząco wpłynąć na wydajność implementacji A*. Pierwszym szczegółem, na który należy zwrócić uwagę, jest to, że sposób, w jaki kolejka priorytetowa obsługuje powiązania, może mieć znaczący wpływ na wydajność w niektórych sytuacjach. Jeśli powiązania zostaną zerwane, więc kolejka będzie zachowywać się w LIFO , A* będzie zachowywać się jak przeszukiwanie w głąb wśród ścieżek o równych kosztach (unikając eksploracji więcej niż jednego równie optymalnego rozwiązania).

Gdy na końcu wyszukiwania wymagana jest ścieżka, często w każdym węźle umieszcza się odniesienie do rodzica tego węzła. Pod koniec wyszukiwania te odniesienia mogą być użyte do odzyskania optymalnej ścieżki. Jeśli te odniesienia są zachowane, może być ważne, aby ten sam węzeł nie pojawiał się w kolejce priorytetów więcej niż raz (każdy wpis odpowiada innej ścieżce do węzła i każdy ma inny koszt). Standardowym podejściem jest tutaj sprawdzenie, czy węzeł, który ma zostać dodany, znajduje się już w kolejce priorytetów. Jeśli tak, to wskaźniki priorytetu i rodzica są zmieniane, aby odpowiadały ścieżce o niższym koszcie. Standardowa na stercie binarnym nie obsługuje bezpośrednio operacji wyszukiwania jednego z jej elementów, ale można ją rozszerzyć o tablicę mieszającą , która odwzorowuje elementy na ich pozycję w stercie, umożliwiając wykonanie tej operacji zmniejszania priorytetu w czas logarytmiczny. Alternatywnie, kopiec Fibonacciego może wykonywać te same operacje o niższym priorytecie w stałym zamortyzowanym czasie .

Przypadki specjalne

Algorytm Dijkstry , jako $kolejny przykład algorytmu wyszukiwania$ postrzegany jako szczególny przypadek A *, wszystkich x . Ogólne przeszukiwanie w głąb można zaimplementować za pomocą A*, biorąc pod uwagę, że istnieje globalny licznik C zainicjowany bardzo dużą wartością. Za każdym razem, gdy przetwarzamy węzeł, przypisujemy C wszystkim jego nowo odkrytym sąsiadom. Po każdym pojedynczym zadaniu zmniejszamy licznik C o jeden. $im$ wcześniej węzeł zostanie wykryty, tym wyższa wartość $każdym$ algorytm Dijkstry, jak i przeszukiwanie w głąb można zaimplementować wydajniej bez uwzględniania węźle

Nieruchomości

Zakończenie i kompletność

Na grafach skończonych z nieujemnymi wagami krawędzi A* ma gwarantowane zakończenie i jest zupełne , tj. zawsze znajdzie rozwiązanie (ścieżkę od początku do celu), jeśli takie istnieje. Na nieskończonych wykresach ze skończonym współczynnikiem rozgałęzienia i kosztami krawędzi, które są ograniczone od zera ( ${\ textstyle d (x, y)> \ varepsilon > 0}$ dla pewnego ustalonego ${\ Displaystyle \ varepsilon }$ ), A* ma gwarancję zakończenia tylko wtedy, gdy istnieje rozwiązanie.

Dopuszczalność

Mówi się, że algorytm wyszukiwania jest dopuszczalny , jeśli gwarantuje zwrócenie rozwiązania optymalnego. Jeśli funkcja heurystyczna używana przez A* jest dopuszczalna , to A* jest dopuszczalna. Intuicyjny „dowód” tego jest następujący:

Kiedy A * kończy wyszukiwanie, znalazł ścieżkę od początku do celu, której rzeczywisty koszt jest niższy niż szacowany koszt dowolnej ścieżki od początku do celu przez dowolny otwarty węzeł (wartość $)$ . Gdy heurystyka jest dopuszczalna, szacunki te są optymistyczne (niezupełnie — patrz następny akapit), więc A* może bezpiecznie zignorować te węzły, ponieważ nie mogą one prowadzić do tańszego rozwiązania niż to, które już posiada. Innymi słowy, A* nigdy nie przeoczy możliwości tańszej ścieżki od początku do celu, więc będzie szukać dalej, aż takie możliwości znikną.

Rzeczywisty dowód jest nieco bardziej skomplikowany, ponieważ $węzłów$ nie gwarantują, że będą optymistyczne, nawet jeśli heurystyka jest dopuszczalna. Dzieje $wartości otwartych$ tak, ponieważ $węzłów nie są$ jako optymalne, więc suma nie gwarantuje, że będzie

Optymalność i spójność

Algorytm A jest optymalnie wydajny w odniesieniu do zbioru alternatywnych algorytmów Alt na zbiorze problemów P , jeśli dla każdego problemu P w P i każdego algorytmu A′ w Alts zbiór węzłów rozwinięty przez A w rozwiązywaniu P jest podzbiorem (prawdopodobnie równe) zbioru węzłów rozszerzonych o A′ w rozwiązywaniu P. Ostateczne badanie optymalnej wydajności A* jest zasługą Riny Dechter i Judei Pearl. Rozważali różne definicje Alt i P w połączeniu z heurystyką A*, która jest jedynie dopuszczalna lub jest zarówno spójna , jak i dopuszczalna. Najciekawszym pozytywnym wynikiem, jaki udowodnili, jest to, że A*, ze spójną heurystyką, jest optymalnie wydajny w odniesieniu do wszystkich dopuszczalnych algorytmów wyszukiwania podobnych do A* we wszystkich ″niepatologicznych″ problemach wyszukiwania. Z grubsza mówiąc, ich pojęcie problemu niepatologicznego jest tym, co teraz rozumiemy przez „do rozstrzygnięcia remisu”. Ten wynik nie jest spełniony, jeśli heurystyka A* jest dopuszczalna, ale niespójna. W takim przypadku Dechter i Pearl wykazali, że istnieją dopuszczalne algorytmy podobne do A*, które mogą rozszerzać arbitralnie mniej węzłów niż A* w niektórych niepatologicznych problemach.

Optymalna wydajność dotyczy zbioru rozwiniętych węzłów, a nie liczby rozwinięć węzłów (liczby iteracji głównej pętli A*). Gdy używana heurystyka jest dopuszczalna, ale niespójna, możliwe jest wielokrotne rozszerzanie węzła o A *, w najgorszym przypadku wykładniczą liczbę razy. W takich okolicznościach algorytm Dijkstry mógłby znacznie przewyższyć A*. Jednak nowsze badania wykazały, że ten patologiczny przypadek występuje tylko w pewnych wymyślonych sytuacjach, w których waga krawędzi grafu wyszukiwania jest wykładnicza w stosunku do rozmiaru grafu i że pewne niespójne (ale dopuszczalne) heurystyki mogą prowadzić do zmniejszonej liczby ekspansji węzłów w wyszukiwaniach A*.

Ograniczony relaks

Wyszukiwanie* wykorzystujące heurystykę, która jest 5,0(=ε) razy spójna heurystyka i uzyskuje ścieżkę nieoptymalną.

Chociaż kryterium dopuszczalności gwarantuje optymalną ścieżkę rozwiązania, oznacza to również, że A* musi zbadać wszystkie równie wartościowe ścieżki, aby znaleźć ścieżkę optymalną. Aby obliczyć przybliżone najkrótsze ścieżki, można przyspieszyć wyszukiwanie kosztem optymalności poprzez złagodzenie kryterium dopuszczalności. Często chcemy ograniczyć tę relaksację, aby zagwarantować, że ścieżka rozwiązania nie będzie gorsza niż (1 + ε ) razy optymalna ścieżka rozwiązania. Ta nowa gwarancja jest określana jako ε -dopuszczalna.

Istnieje kilka algorytmów dopuszczalnych ε :

• Ważone A*/Wagi statyczne. Jeśli h _a ( n ) jest dopuszczalną funkcją heurystyczną, w ważonej wersji wyszukiwania A* używa się h _w ( n ) = ε h _a ( n ) , ε > 1 jako funkcji heurystycznej i przeprowadza się wyszukiwanie A* jak zwykle (co ostatecznie dzieje się szybciej niż przy użyciu h _a, ponieważ rozwijanych jest mniej węzłów). Ścieżka znaleziona w ten sposób przez algorytm wyszukiwania może mieć koszt co najwyżej ε razy większy niż ścieżka o najniższym koszcie na grafie.
• Ważenie dynamiczne wykorzystuje funkcję kosztu ${\ Displaystyle f (n) = g (n) + (1+ \ varepsilon w (n) }) h (n)}$ , gdzie ${\ Displaystyle w (n) = {\ rozpocząć {przypadki} 1 - {\ Frac {d (n)} {N}} & d (n) \ równoważnik N \\ 0& {\ tekst {inaczej}} \ koniec {przypadków}}} i gdzie jest głębokość re ( n ) {$ \ Displaystyle $}$ poszukiwań, a N to przewidywana długość ścieżki rozwiązania.
• Próbkowane ważenie dynamiczne wykorzystuje próbkowanie węzłów w celu lepszego oszacowania i odchylenia błędu heurystycznego.
• ${\ Displaystyle A _ {\ varepsilon} ^ {*}}$ . używa dwóch funkcji heurystycznych. Pierwsza to lista FOCAL, która służy do wybierania węzłów kandydujących, a druga h _F służy do wybierania najbardziej obiecującego węzła z listy FOCAL.
• A _ε wybiera węzły za pomocą funkcji , gdzie A i B są stałymi. ${\ Displaystyle Af (n) + Bh_ {F} (n)}$ Jeśli $węzłów$ cofnie z funkcją gdzie C
• Alpha* próbuje promować eksploatację w głąb, preferując niedawno rozbudowane węzły. Alpha* używa funkcji kosztu ${\ Displaystyle f _ {\ alfa} (n) = (1 + w_ {\ alfa} (n)) f (n)}$ , gdzie ${\ Displaystyle w _ {\ alfa} (n) = {\ rozpocząć {przypadki} \ lambda & g (\pi (n))\leq g({\tylda {n}})\\\Lambda &{\text{inaczej}}\end{przypadki}}} , gdzie λ$ i Λ są stałymi z ${ \displaystyle \lambda \leq \Lambda }$ , π ( n ) jest rodzicem n , a ñ jest ostatnio rozwiniętym węzłem.

Złożoność

Złożoność czasowa A* zależy od heurystyki. W najgorszym przypadku nieograniczonej przestrzeni poszukiwań liczba rozwiniętych węzłów jest wykładnicza w głębi rozwiązania (najkrótsza ścieżka) d : O ( b ^d ) , gdzie b jest współczynnikiem rozgałęzienia (średnia liczba następców na stan ). Zakłada to, że stan docelowy w ogóle istnieje i jest osiągalny ze stanu początkowego; jeśli tak nie jest, a przestrzeń stanów jest nieskończona, algorytm nie zakończy się.

Funkcja heurystyczna ma duży wpływ na praktyczną wydajność wyszukiwania A*, ponieważ dobra heurystyka pozwala A* odciąć wiele węzłów b ^d , które rozszerzyłoby wyszukiwanie bez informacji. Jego jakość można wyrazić za pomocą efektywnego współczynnika rozgałęzienia b * , który można określić empirycznie dla instancji problemu, mierząc liczbę węzłów generowanych przez rozwinięcie, N , oraz głębokość rozwiązania, a następnie rozwiązując

${\ Displaystyle N + 1 = 1 + b ^ {*} + (b ^ {*}) ^ {2} + \ kropki + (b ^ {*}) ^ {d}.}$

Dobre heurystyki to te, które mają niski efektywny współczynnik rozgałęzienia (optymalny to b * = 1 ).

Złożoność czasowa jest wielomianowa , gdy przestrzeń poszukiwań jest drzewem, istnieje jeden stan docelowy, a funkcja heurystyczna h spełnia warunek:

${\ Displaystyle | h (x) -h ^ {*} (x) | = O (\ log h ^ {*} (x))}$

gdzie h ^* jest optymalną heurystyką, dokładnym kosztem przejścia od x do celu. Innymi słowy, błąd h nie będzie rósł szybciej niż logarytm „doskonałej heurystyki” h ^* , która zwraca rzeczywistą odległość od x do celu.

Złożoność przestrzenna A* jest mniej więcej taka sama jak wszystkich innych algorytmów przeszukiwania grafów, ponieważ wszystkie wygenerowane węzły są przechowywane w pamięci. W praktyce okazuje się to największą wadą wyszukiwania A*, prowadzącą do rozwoju wyszukiwań heurystycznych ograniczonych pamięcią, takich jak iteracyjne pogłębianie A* , A* ograniczone pamięcią i SMA* .

Aplikacje

A* jest często używany do rozwiązywania typowych problemów ze znalezieniem ścieżki w aplikacjach takich jak gry wideo, ale pierwotnie został zaprojektowany jako ogólny algorytm przechodzenia przez graf. Znajduje zastosowanie w różnorodnych problemach, w tym w problemie parsowania przy użyciu gramatyk stochastycznych w NLP . Inne przypadki obejmują wyszukiwanie informacyjne z nauką online.

Relacje z innymi algorytmami

Tym, co odróżnia A* od zachłannego algorytmu wyszukiwania „najlepiej najpierw”, jest to, że bierze on pod uwagę koszt/odległość już przebytą, g ( n ) .

Niektóre popularne warianty algorytmu Dijkstry można postrzegać jako szczególny przypadek A *, gdzie heurystyka dla wszystkich węzłów jest równa ${\ displaystyle h (n) = 0} ;$ z kolei zarówno Dijkstra, jak i A* są szczególnymi przypadkami programowania dynamicznego . A* sam w sobie jest szczególnym przypadkiem uogólnienia branch ibound .

Warianty

• zawsze
• Blok A*
• D*
• Pole D*
• Grzywka
• Oszczędność frędzli A* (FSA*)
• Uogólniony adaptacyjny A* (GAA*)
• Przyrostowe wyszukiwanie heurystyczne
• Zredukowane A*
• Pogłębianie iteracyjne A* (IDA*)
• Wyszukiwanie punktu przeskoku
• Planowanie na całe życie A* (LPA*)
• Nowy dwukierunkowy A* (NBA*)
• Uproszczona pamięć ograniczona A* (SMA*)
• Teta*

A* można również dostosować do algorytmu wyszukiwania dwukierunkowego . Szczególną uwagę należy zwrócić na kryterium zatrzymania.

Zobacz też

• Wyszukiwanie wszerz
• Wyszukiwanie w głąb
• Planowanie ścieżki pod dowolnym kątem , szukaj ścieżek, które nie ograniczają się do poruszania się wzdłuż krawędzi grafu, ale mogą przyjąć dowolny kąt

Dalsza lektura

•   Nilsson, NJ (1980). Zasady sztucznej inteligencji . Palo Alto, Kalifornia: Tioga Publishing Company. ISBN 978-0-935382-01-3 .

Linki zewnętrzne

• Wariacja na temat A* o nazwie Hierarchical Path-Finding A* (HPA*)
• Briana Grinsteada. „Algorytm wyszukiwania A* w JavaScript (zaktualizowany)” . Zarchiwizowane od oryginału w dniu 15 lutego 2020 r . Źródło 8 lutego 2021 r .