Analiza bilansu strumienia

Analiza równowagi strumienia ( FBA ) to matematyczna metoda symulacji metabolizmu w rekonstrukcjach sieci metabolicznych w skali genomu . W porównaniu z tradycyjnymi metodami modelowania FBA jest mniej intensywna pod względem danych wejściowych wymaganych do budowy modelu. Symulacje przeprowadzane przy użyciu FBA są niedrogie obliczeniowo i umożliwiają obliczenie strumieni metabolicznych w stanie ustalonym dla dużych modeli (ponad 2000 reakcji) w ciągu kilku sekund na nowoczesnych komputerach osobistych. Powiązana metoda analizy szlaków metabolicznych ma na celu znalezienie i wypisanie wszystkich możliwych szlaków między metabolitami.

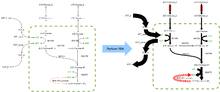
Wyniki FBA na przygotowanej sieci metabolicznej sześciu najważniejszych reakcji glikolizy . Przewidywany strumień przechodzący przez każdą reakcję jest proporcjonalny do szerokości linii. Funkcja celu na czerwono, ograniczenia importu alfa-D-glukozy i beta-D-glukozy przedstawione jako czerwone słupki.

FBA znajduje zastosowanie w inżynierii bioprocesowej do systematycznej identyfikacji modyfikacji sieci metabolicznych drobnoustrojów stosowanych w procesach fermentacji, które poprawiają wydajność produktów chemikaliów ważnych dla przemysłu, takich jak etanol i kwas bursztynowy. Został również wykorzystany do identyfikacji domniemanych celów leków w raku i patogenach, racjonalnego projektowania pożywek hodowlanych i interakcji gospodarz-patogen . Wyniki FBA można zwizualizować za pomocą map strumieni podobnych do obrazu po prawej stronie, który ilustruje strumienie w stanie ustalonym przenoszone przez reakcje glikolizy . Grubość strzałek jest proporcjonalna do strumienia przechodzącego przez reakcję.

FBA formalizuje układ równań opisujących zmiany stężenia w sieci metabolicznej jako iloczyn skalarny macierzy współczynników stechiometrycznych (macierz stechiometryczna S ) i wektora v strumieni nierozwiązanych. Prawa strona iloczynu skalarnego to wektor zer reprezentujący system w stanie ustalonym . Programowanie liniowe jest następnie wykorzystywane do obliczania rozwiązania strumieni odpowiadających stanowi ustalonemu.

Historia

Niektóre z najwcześniejszych prac w FBA pochodzą z wczesnych lat 80. Papoutsakis wykazał, że możliwe jest skonstruowanie równań bilansu strumienia przy użyciu mapy metabolicznej. Jednak to Watson jako pierwszy przedstawił pomysł wykorzystania programowania liniowego i funkcji celu do rozwiązania strumieni na ścieżce. Pierwsze znaczące badanie zostało następnie opublikowane przez Fell i Small, którzy wykorzystali analizę bilansu strumienia wraz z bardziej rozbudowanymi funkcjami celu do zbadania ograniczeń w syntezie tłuszczu.

Symulacje

Przykład nieśmiercionośnej delecji genu w próbce sieci metabolicznej z przepływami pokazanymi przez masę linii reakcyjnych obliczoną przez FBA. Tutaj przepływ przez funkcję celu jest zmniejszony o połowę, ale nadal jest obecny.

Przykład letalnej delecji genu w próbce sieci metabolicznej z przepływami pokazanymi przez masę linii reakcyjnych obliczoną przez FBA. Tutaj nie ma przepływu przez funkcję celu, co symuluje, że ścieżka nie jest już funkcjonalna.

Zahamowanie reakcji: Wykres przewidywanego tempa wzrostu FBA (oś y) do zmniejszającego się dopływu tlenu (oś x) w modelu E.coli FBA. ^{[ potrzebne źródło ]}

Trójwymiarowa płaszczyzna fazy fenotypowej przedstawiająca wpływ różnych przepływów wejściowych glukozy i glicerolu na tempo wzrostu Mycobacterium tuberculosis. Oś X reprezentuje napływ glicerolu, a oś Y reprezentuje napływ glukozy, wysokość powierzchni (czerwona) reprezentuje wartość strumienia wzrostu dla każdej kombinacji strumieni wejściowych. ^{[ potrzebne źródło ]}

Wersja wykresu poziomu płaszczyzny fazy fenotypowej przedstawiająca wpływ różnych przepływów wejściowych glukozy i glicerolu na tempo wzrostu Mycobacterium tuberculosis. Oś X reprezentuje napływ glicerolu, a oś Y przedstawia napływ glukozy, kolor reprezentuje wartość strumienia wzrostu. ^{[ potrzebne źródło ]}

Porównanie wykresów korelacji śmiertelnych delecji reakcji parami w różnych podsystemach dla E.coli (po lewej) i M.tuberculosis (po prawej). ^{[ potrzebne źródło ]}

FBA nie wymaga intensywnych obliczeń, a obliczenie optymalnych strumieni do produkcji biomasy dla typowej sieci zajmuje kilka sekund (około 2000 reakcji). Oznacza to, że efekt usuwania reakcji z sieci i/lub zmiany ograniczeń strumienia można sensownie modelować na jednym komputerze.

Badania delecji genów/reakcji i zaburzeń

Usuwanie pojedynczej reakcji

Często stosowana technika przeszukiwania sieci metabolicznej pod kątem reakcji szczególnie krytycznych dla produkcji biomasy. Usuwając po kolei każdą reakcję w sieci i mierząc przewidywany przepływ przez funkcję biomasy, każdą reakcję można sklasyfikować jako istotną (jeśli przepływ przez funkcję biomasy jest znacznie zmniejszony) lub nieistotną (jeśli przepływ przez funkcję biomasy funkcja pozostaje niezmieniona lub tylko nieznacznie zmniejszona).

Usuwanie reakcji parami

Usuwanie parami reakcji wszystkich możliwych par reakcji jest przydatne przy poszukiwaniu celów dla leków, ponieważ umożliwia symulację leczenia z wieloma celami, albo za pomocą pojedynczego leku z wieloma celami, albo kombinacji leków. Badania podwójnej delecji mogą również określić ilościowo syntetyczne śmiertelne interakcje między różnymi ścieżkami, dostarczając miarę udziału ścieżki w ogólnej odporności sieci.

Pojedyncze i wielokrotne delecje genów

Geny są połączone z reakcjami katalizowanymi przez enzymy za pomocą wyrażeń boolowskich, znanych jako wyrażenia reakcji gen-białko-reakcja (GPR). Zazwyczaj GPR przyjmuje postać (gen A ORAZ gen B), aby wskazać, że produkty genów A i B są podjednostkami białkowymi, które łączą się, tworząc kompletne białko, a zatem brak któregokolwiek z nich skutkowałby usunięciem reakcji. Z drugiej strony, jeśli GPR to (gen A LUB gen B), oznacza to, że produktami genów A i B są izozymy . W związku z tym możliwa jest ocena wpływu delecji pojedynczego lub wielu genów przez ocenę GPR jako wyrażenia logicznego. Jeśli georadar ma wartość false , reakcja jest ograniczana do zera w modelu przed wykonaniem FBA. W ten sposób nokauty genów można symulować za pomocą FBA.

Interpretacja wyników delecji genów i reakcji

Przydatność analiz inhibicji reakcji i delecji staje się najbardziej widoczna, jeśli zestawiono macierz reakcji gen-białko dla sieci badanej za pomocą FBA. Macierz reakcji gen-białko to macierz binarna łącząca geny z białkami z nich wykonanymi. Korzystając z tej macierzy, istotność reakcji można przekształcić w niezbędność genów, wskazując defekty genów, które mogą powodować określony fenotyp choroby lub białka/enzymy, które są niezbędne (a zatem, które enzymy są najbardziej obiecującymi celami leków w patogenach). Jednak macierz reakcji gen-białko nie określa relacji boolowskiej między genami w odniesieniu do enzymu, zamiast tego wskazuje jedynie na związek między nimi. Dlatego należy go używać tylko wtedy, gdy wyrażenie boolowskie GPR jest niedostępne.

Hamowanie reakcji

Efekt zahamowania reakcji, zamiast jej całkowitego usunięcia, można symulować w FBA, ograniczając dozwolony przepływ przez nią. Efekt zahamowania można sklasyfikować jako śmiertelny lub nieśmiercionośny, stosując te same kryteria, co w przypadku delecji, gdzie stosuje się odpowiedni próg do odróżnienia „znacznie zmniejszonego” od „nieznacznie zmniejszonego”. Ogólnie wybór progu jest arbitralny, ale rozsądne oszacowanie można uzyskać z eksperymentów wzrostu, w których faktycznie przeprowadza się symulowane inhibicje/delecje i mierzy się tempo wzrostu.

Optymalizacja podłoża wzrostowego

W celu zaprojektowania optymalnej pożywki wzrostowej w odniesieniu do zwiększonego tempa wzrostu lub wydzielania użytecznych produktów ubocznych, możliwe jest zastosowanie metody znanej jako analiza płaszczyzny fazy fenotypowej. PhPP obejmuje wielokrotne stosowanie FBA na modelu, jednocześnie zmieniając ograniczenia pobierania składników odżywczych i obserwując wartość funkcji celu (lub przepływów produktów ubocznych). PhPP umożliwia znalezienie optymalnej kombinacji składników odżywczych, które faworyzują określony fenotyp lub tryb metabolizmu, co skutkuje wyższym tempem wzrostu lub wydzielaniem produktów ubocznych przydatnych w przemyśle. Wykazano, że przewidywane tempo wzrostu bakterii w różnych pożywkach dobrze koreluje z wynikami eksperymentów, a także określa precyzyjne minimalne pożywki dla hodowli Salmonella typhimurium .

Interakcje gospodarz-patogen

Ludzka mikrobiota to złożony system, w którym znajduje się aż 400 bilionów drobnoustrojów i bakterii wchodzących w interakcje między sobą i gospodarzem. Aby zrozumieć kluczowe czynniki w tym systemie; proponuje się wieloskalową, dynamiczną analizę bilansu strumienia, ponieważ FBA jest klasyfikowany jako mniej intensywny obliczeniowo.

Opis matematyczny

W przeciwieństwie do tradycyjnie stosowanego podejścia do modelowania metabolizmu przy użyciu sprzężonych równań różniczkowych zwyczajnych , analiza bilansu strumieni wymaga bardzo niewielu informacji pod względem parametrów kinetycznych enzymu i stężenia metabolitów w układzie. Osiąga to poprzez dwa założenia, stan ustalony i optymalność. Pierwszym założeniem jest to, że modelowany układ wszedł w stan ustalony, w którym stężenia metabolitów już się nie zmieniają, tj. w każdym węźle metabolitu strumienie wytwarzania i zużycia wzajemnie się znoszą. Drugie założenie jest takie, że organizm został zoptymalizowany przez ewolucję dla jakiegoś celu biologicznego, takiego jak optymalny wzrost lub ochrona zasobów. Założenie stanu ustalonego redukuje układ do zestawu równań liniowych, które następnie rozwiązuje się w celu znalezienia rozkładu strumienia, który spełnia warunek stanu ustalonego z zastrzeżeniem ograniczeń stechiometrycznych, jednocześnie maksymalizując wartość pseudoreakcji (funkcja celu) reprezentujący konwersję prekursorów biomasy w biomasę.

Założenie stanu stacjonarnego wywodzi się z idei równowagi materiałowej opracowanej w celu modelowania wzrostu komórek drobnoustrojów w fermentorach w inżynierii bioprocesowej. Podczas wzrostu drobnoustrojów substrat składający się ze złożonej mieszaniny źródeł węgla, wodoru, tlenu i azotu wraz z pierwiastkami śladowymi jest zużywany w celu wytworzenia biomasy. Model bilansu materiałowego dla tego procesu przyjmuje postać:

\ Displaystyle \ operatorname {wejście} = \ operatorname {wyjście} + \ operatorname {akumulacja}}

Jeśli uznamy, że układ komórek drobnoustrojów jest w stanie ustalonym, to możemy ustawić składnik akumulacji na zero i sprowadzić równania bilansu materiałowego do prostych równań algebraicznych. W takim systemie substrat staje się wejściem do systemu, który jest zużywany, a produkowana biomasa staje się wyjściem z systemu. Bilans materiałowy można zatem przedstawić jako:

{\ Displaystyle \ operatorname {wejście} = \ operatorname {wyjście}}

{\ Displaystyle \ operatorname {wejście} - \ matematyczna {Wyjście} =\ matematyczna {0} }

Matematycznie równania algebraiczne można przedstawić jako iloczyn skalarny macierzy współczynników i wektora niewiadomych. Ponieważ założenie stanu ustalonego stawia termin akumulacji na zero. System można zapisać jako:

{\ Displaystyle \ qquad A \ cdot \ mathbf {x} = \ mathbf {0}}

Rozszerzając ten pomysł na sieci metaboliczne, możliwe jest przedstawienie sieci metabolicznej jako zrównoważonego stechiometrycznie zestawu równań. Przechodząc do formalizmu macierzowego, możemy przedstawić równania jako iloczyn skalarny macierzy współczynników stechiometrycznych ( macierz stechiometryczna $i$ wektor strumieni $i$ niewiadome ustaw prawą stronę na 0, co oznacza stan ustalony.

{\ Displaystyle \ qquad S \ cdot \ mathbf {v} = \ mathbf {0}}

Sieci metaboliczne zwykle mają więcej reakcji niż metabolitów, co daje niedookreślony układ równań liniowych zawierających więcej zmiennych niż równań. Standardowym podejściem do rozwiązywania takich niedookreślonych systemów jest zastosowanie programowania liniowego .

Programy liniowe to problemy, które można wyrazić w postaci kanonicznej :

{\ Displaystyle {\ rozpocząć {wyrównane} i {\ tekst {maksymalizować}} && \ mathbf {c} ^ {\ operatorname {T}} \ mathbf {x} \ \&{\text{podlega}}&&A\mathbf {x} \leq \mathbf {b} \\&{\text{i}}&&\mathbf {x} \geq \mathbf {0} \end{wyrównane }}}

gdzie x reprezentuje wektor zmiennych (do określenia), c i b są wektorami (znanych) współczynników, A jest (znaną) macierzą współczynników i ${\ Displaystyle (\ cdot) ^ {\ operatorname {T} }}$ to transpozycja macierzy . Wyrażenie, które ma zostać zmaksymalizowane lub zminimalizowane, nazywane jest funkcją celu ( w tym przypadku c ^T x ). Nierówności A x ≤ b są ograniczeniami określającymi polytope wypukły , na którym funkcja celu ma być optymalizowana.

Programowanie liniowe wymaga zdefiniowania funkcji celu. Za optymalne rozwiązanie problemu LP uważa się rozwiązanie, które maksymalizuje lub minimalizuje wartość funkcji celu w zależności od przypadku. W przypadku analizy bilansu strumieni funkcja celu Z dla LP jest często definiowana jako produkcja biomasy. Produkcja biomasy jest symulowana za pomocą równania reprezentującego reakcję skupioną, która przekształca różne prekursory biomasy w jedną jednostkę biomasy.

Dlatego kanoniczna postać problemu analizy bilansu strumienia byłaby następująca:

{\ Displaystyle {\ rozpocząć {wyrównane} i {\ tekst {maksymalizować}} &&\mathbf {c} ^{\mathrm {T} }\mathbf {v} \\&{\text{podlega}}&&S\mathbf {v} =\mathbf {0} \\&{\text{i }}&&\mathbf {dolna granica} \leq \mathbf {v} \leq \mathbf {górna granica} \end{wyrównane}}}

gdzie $reprezentuje wektor$ $strumieni$ (do ustalenia), jest (znaną współczynników . Wyrażenie, które ma być zmaksymalizowane lub zminimalizowane, nazywane jest funkcją celu ( w tym przypadku do $\ Displaystyle \ mathbf {c} ^ {\ operatorname {T}} \ mathbf {v}}) .$ l ${\ Displaystyle \ mathbf {dolna granica} \ równoważnik \ mathbf {v}}$ v $\ mathbf {górna granica}}$ $\ Displaystyle \ mathbf {v} } \$ $macierzy$ zdefiniuj odpowiednio minimalne i maksymalne szybkości strumienia dla każdej reakcji odpowiadającej kolumnom . Szybkości te można określić eksperymentalnie, aby jeszcze bardziej ograniczyć i poprawić predykcyjną dokładność modelu, lub można je określić na dowolnie wysoką wartość wskazującą na brak ograniczeń strumienia przechodzącego przez reakcję.

Główną zaletą podejścia opartego na bilansie strumienia jest to, że nie wymaga ono żadnej wiedzy na temat stężeń metabolitów ani, co ważniejsze, kinetyki enzymów w układzie; założenie homeostazy wyklucza potrzebę znajomości stężeń metabolitów w dowolnym momencie, o ile ta ilość pozostaje stała, a dodatkowo eliminuje potrzebę określonych praw szybkości , ponieważ zakłada, że w stanie ustalonym nie ma zmiany wielkości metabolitu basen w systemie. Same współczynniki stechiometryczne są wystarczające do matematycznej maksymalizacji określonej funkcji celu .

Funkcja celu jest zasadniczo miarą tego, w jaki sposób każdy element systemu przyczynia się do produkcji pożądanego produktu. Sam produkt zależy od przeznaczenia modelu, ale jednym z najczęstszych przykładów jest badanie całkowitej biomasy. Godnym uwagi przykładem sukcesu FBA jest zdolność do dokładnego przewidywania tempa wzrostu prokariotycznej E. coli hodowanej w różnych warunkach. W tym przypadku system metaboliczny został zoptymalizowany, aby zmaksymalizować funkcję celu biomasy. Jednak model ten można wykorzystać do optymalizacji produkcji dowolnego produktu i jest często używany do określenia poziomu wyjściowego niektórych produktów istotnych z punktu widzenia biotechnologii . Sam model można zweryfikować eksperymentalnie, hodując organizmy przy użyciu chemostatu lub podobnych narzędzi, aby zapewnić utrzymanie stałego stężenia składników odżywczych. Pomiary produkcji pożądanego obiektywu można następnie wykorzystać do skorygowania modelu.

Dobry opis podstawowych koncepcji FBA można znaleźć w ogólnodostępnym materiale dodatkowym do Edwards et al. 2001, które można znaleźć na stronie internetowej Nature. Dalsze źródła obejmują książkę „Systems Biology” B. Palssona poświęconą temu tematowi oraz przydatny samouczek i artykuł J. Ortha. W opublikowanej literaturze naukowej istnieje wiele innych źródeł informacji na temat tej techniki, w tym Lee i in. 2006, Feist i in. 2008 oraz Lewis i in. 2012.

Przygotowanie i udoskonalenie modelu

Kluczowymi częściami przygotowania modelu są: stworzenie sieci metabolicznej bez luk, dodanie ograniczeń do modelu i wreszcie dodanie funkcji celu (często nazywanej funkcją biomasy), zwykle w celu symulacji wzrostu modelowanego organizmu.

Sieć metaboliczna i narzędzia programowe

Pierwsze sześć reakcji w Glycolysis przygotowanych dla FBA poprzez dodanie funkcji celu (czerwona) oraz importu i eksportu składników odżywczych (ATP, ADP, BDG, ADG) przez granicę systemu (przerywana zielona linia).

Sieci metaboliczne mogą mieć różny zakres, od tych opisujących pojedynczą ścieżkę , aż po komórkę , tkankę lub organizm . Głównym wymaganiem sieci metabolicznej, która stanowi podstawę sieci gotowej do FBA, jest brak luk. Zwykle oznacza to, że wymagana jest obszerna ręczna kuracja, co sprawia, że przygotowanie sieci metabolicznej do analizy bilansu strumienia jest procesem, który może zająć miesiące lub lata. Jednak ostatnie postępy, takie jak tak zwane metody wypełniania luk, mogą skrócić wymagany czas do tygodni lub miesięcy.

Pakiety oprogramowania do tworzenia modeli FBA obejmują: Pathway Tools/MetaFlux , Simpheny, MetNetMaker, COBRApy, CarveMe, MIOM lub COBREXA.jl.

Generalnie modele są tworzone w formacie BioPAX lub SBML , aby dalsza analiza lub wizualizacja mogła odbywać się w innym oprogramowaniu, chociaż nie jest to wymagane.

Ograniczenia

Kluczową częścią FBA jest możliwość dodawania ograniczeń do szybkości strumienia reakcji w sieciach, zmuszając je do pozostania w zakresie wybranych wartości. Dzięki temu model dokładniej symuluje rzeczywisty metabolizm. Z biologicznego punktu widzenia ograniczenia należą do dwóch podzbiorów; ograniczenia graniczne, które ograniczają pobieranie/wydalanie składników odżywczych oraz ograniczenia wewnętrzne, które ograniczają przepływ poprzez reakcje w organizmie. W kategoriach matematycznych można rozważyć zastosowanie ograniczeń w celu zmniejszenia przestrzeni rozwiązań modelu FBA. Oprócz ograniczeń nałożonych na brzegach sieci metabolicznej, ograniczenia można zastosować do reakcji zachodzących głęboko w sieci. Te ograniczenia są zwykle proste; mogą ograniczać kierunek reakcji ze względów energetycznych lub ograniczać maksymalną prędkość reakcji ze względu na skończoną prędkość wszystkich reakcji w przyrodzie.

Ograniczenia dotyczące podłoża wzrostowego

Organizmy i wszystkie inne systemy metaboliczne wymagają pewnego wkładu składników odżywczych. Zazwyczaj szybkość wchłaniania składników odżywczych jest podyktowana ich dostępnością (składnik odżywczy, którego nie ma, nie może zostać wchłonięty), ich stężeniem i stałymi dyfuzji (wyższe stężenia szybko dyfuzujących metabolitów są szybciej wchłaniane) oraz sposobem wchłaniania (np. transport aktywny lub dyfuzja ułatwiona a dyfuzja prosta).

Jeśli szybkość wchłaniania (i/lub wydalania) niektórych składników odżywczych można zmierzyć eksperymentalnie, wówczas informacje te można dodać jako ograniczenie szybkości przepływu na krawędziach modelu metabolicznego. Zapewnia to, że składniki odżywcze, które nie są obecne lub nie są wchłaniane przez organizm, nie wchodzą w jego metabolizm (szybkość przepływu jest ograniczona do zera), a także oznacza, że symulacja przestrzega znanych szybkości wchłaniania składników odżywczych. Zapewnia to drugorzędną metodę upewnienia się, że symulowany metabolizm ma właściwości zweryfikowane eksperymentalnie, a nie tylko te, które są akceptowalne matematycznie.

Więzy termodynamiczne reakcji

W zasadzie wszystkie reakcje są odwracalne, jednak w praktyce reakcje często zachodzą skutecznie tylko w jednym kierunku. Może to wynikać ze znacznie wyższego stężenia reagentów w porównaniu ze stężeniem produktów reakcji. Ale częściej dzieje się tak, ponieważ produkty reakcji mają znacznie niższą energię swobodną niż reagenty, a zatem kierunek reakcji do przodu jest bardziej preferowany.

Dla idealnych reakcji,

{\ Displaystyle - \ infty <v_ {i}<\ infty \,}

W przypadku niektórych reakcji można zastosować ograniczenie termodynamiczne implikujące kierunek (w tym przypadku do przodu)

{\ Displaystyle 0 <v_ {i}<\ infty \,}

Realistycznie przepływ przez reakcję nie może być nieskończony (biorąc pod uwagę, że enzymy w rzeczywistym systemie są skończone), co implikuje, że

{\ Displaystyle 0 <v_ {i}<v_ {\ max} \,}

Eksperymentalnie zmierzone ograniczenia strumienia

Pewne szybkości przepływu można zmierzyć eksperymentalnie ( $a$ strumienie w modelu metabolicznym można ograniczyć z pewnym błędem ( $varepsilon \,$ ) , aby upewnić się, że te znane szybkości strumienia są dokładnie odtworzone w symulacji.

{\ Displaystyle v_ {i, m} - \ varepsilon <v_ {i}<v_ {i, m} + \ varepsilon \,}

Natężenia przepływu najłatwiej zmierzyć pod kątem wchłaniania składników odżywczych na krawędzi sieci. Pomiary strumieni wewnętrznych są możliwe przy użyciu metabolitów znakowanych radioaktywnie lub widocznych w NMR.

Gotowe modele metaboliczne z ograniczeniami FBA można analizować za pomocą oprogramowania, takiego jak zestaw narzędzi COBRA (dostępne implementacje w MATLAB i Python ), SurreyFBA lub internetowy FAME. Dodatkowe pakiety oprogramowania zostały wymienione w innym miejscu. Niedawno dokonano przeglądu kompleksowego przeglądu całego takiego oprogramowania i jego funkcjonalności.

Alternatywa typu open source jest dostępna w R (języku programowania) jako pakiety abcdeFBA lub sybil do wykonywania FBA i innych technik modelowania opartych na ograniczeniach.

Funkcja celu

FBA może podać dużą liczbę akceptowalnych matematycznie rozwiązań problemu stanu ustalonego ${\ Displaystyle (S {\ vec {v}} = 0)}$ . Jednak roztwory o znaczeniu biologicznym to te, które wytwarzają pożądane metabolity we właściwej proporcji. Funkcja celu określa proporcję tych metabolitów. Na przykład podczas modelowania wzrostu organizmu funkcja celu jest ogólnie definiowana jako biomasa. Matematycznie jest to kolumna w macierzy stechiometrii, której wpisy określają „zapotrzebowanie” lub działają jak „zlew” na prekursory biosyntezy, takie jak kwasy tłuszczowe, aminokwasy i składniki ściany komórkowej, które są obecne w odpowiednich rzędach S matryca. Wpisy te reprezentują zmierzone eksperymentalnie proporcje suchej masy składników komórkowych. Dlatego ta kolumna staje się skupioną reakcją, która symuluje wzrost i reprodukcję. Dlatego dokładność pomiarów eksperymentalnych odgrywa zasadniczą rolę w prawidłowym zdefiniowaniu funkcji biomasy i sprawia, że wyniki FBA mają zastosowanie biologiczne, zapewniając, że właściwa proporcja metabolitów jest wytwarzana w wyniku metabolizmu.

Podczas modelowania mniejszych sieci można odpowiednio zmienić funkcję celu. Przykładem tego może być badanie metabolizmu węglowodanów , gdzie funkcja celu zostałaby prawdopodobnie zdefiniowana jako pewna proporcja ATP i NADH , a tym samym symulowałaby wytwarzanie metabolitów o wysokiej energii przez ten szlak.

Optymalizacja funkcji cel/biomasa

Programowanie liniowe może być wykorzystane do znalezienia jednego optymalnego rozwiązania. Najczęstszym celem optymalizacji biologicznej dla sieci metabolicznej całego organizmu byłoby wybranie wektora strumienia, $maksymalizuje$ przez funkcję biomasy złożoną z metabolitów składowych organizmu umieszczonego do macierzy stechiometrycznej i oznaczonej ${\ Displaystyle v _$ po prostu ${\ textrm {biomasa}}$

{\ Displaystyle \ max _ {\ vec {v}} \ v_ {b} \ qquad {\ textrm {st}} \ qquad \ mathbf {S} \, {\ vec {v}} = 0}

W bardziej ogólnym przypadku można zdefiniować dowolną reakcję i dodać ją do funkcji biomasy pod warunkiem, że zostanie ona zmaksymalizowana lub zminimalizowana, jeśli pożądane jest pojedyncze „optymalne” rozwiązanie. Alternatywnie, w najbardziej ogólnym przypadku, można wprowadzić wektor, który definiuje ważony zestaw reakcji, które model programowania liniowego powinien dążyć do maksymalizacji lub minimalizacji, c → {\ $\ vec {c}}}$

{\ Displaystyle \ max _ {\ vec {v}} \ {\ vec {v}} \ cdot {\ vec {c}} \ qquad {\ textrm {st}}\qquad \mathbf {S} \,{\vec {v}}=0.}

W przypadku istnienia tylko jednej oddzielnej funkcji / reakcji biomasy w macierzy stechiometrycznej $uprościłoby się$ zer o wartości 1 (lub dowolnej wartości niezerowej) w pozycję odpowiadającą tej funkcji biomasy. Tam $,$ gdzie było wiele oddzielnych funkcji celu uprościłoby się do wszystkich zer z wartościami ważonymi na pozycjach odpowiadających wszystkim funkcjom celu

Zmniejszenie przestrzeni rozwiązań – biologiczne względy dla systemu

Analiza przestrzeni zerowej macierzy jest realizowana w pakietach oprogramowania wyspecjalizowanych do operacji na macierzach, takich jak Matlab i Octave. Określenie przestrzeni zerowej $.$ nam o wszystkich możliwych zbiorach wektorów strumienia (lub ich liniowych kombinacji), które równoważą strumienie w sieci biologicznej Zaleta tego podejścia staje się widoczna w układach biologicznych, które są opisywane układami równań różniczkowych z wieloma niewiadomymi. Prędkości w powyższych równaniach różniczkowych - $-$ $zależą$ od podstawowych równań Prędkości są generalnie zaczerpnięte z teorii kinetycznej Michaelisa-Mentena , która obejmuje parametry kinetyczne enzymów katalizujących reakcje oraz stężenie samych metabolitów. Wyizolowanie enzymów z organizmów żywych i pomiar ich parametrów kinetycznych jest trudnym zadaniem, podobnie jak pomiar wewnętrznych stężeń i stałych dyfuzji metabolitów w organizmie. Dlatego podejście równań różniczkowych do modelowania metabolicznego wykracza poza obecny zakres nauki dla wszystkich organizmów z wyjątkiem większości badanych. FBA omija tę przeszkodę, stosując założenie homeostatyczne, które jest rozsądnie przybliżonym opisem systemów biologicznych.

Chociaż FBA omija tę biologiczną przeszkodę, pozostaje matematyczny problem dużej przestrzeni rozwiązań. FBA ma dwojaki cel. Dokładne odwzorowanie biologicznych granic systemu i przywrócenie rozkładu strumienia najbliższego naturalnym przepływom w docelowym systemie/organizmie. Pewne zasady biologiczne mogą pomóc przezwyciężyć trudności matematyczne. Chociaż macierz stechiometryczna jest początkowo prawie zawsze niedookreślona (co oznacza, że przestrzeń rozwiązań do jest bardzo duża), ${\ displaystyle \ scriptstyle \ mathbf {S} \, {\ vec {v}} = 0}$ rozmiar przestrzeni rozwiązań można zmniejszyć i uczynić ją bardziej odzwierciedlającą biologię problemu poprzez nałożenie pewnych ograniczeń na rozwiązania.

Rozszerzenia

Sukces FBA i uświadomienie sobie jego ograniczeń doprowadziły do rozszerzeń, które próbują pośredniczyć w ograniczeniach tej techniki.

Analiza zmienności strumienia

Wizualna i numeryczna reprezentacja FVA w kompletnej sieci.

Optymalne rozwiązanie problemu bilansu strumienia rzadko jest unikalne, ponieważ istnieje wiele możliwych i równie optymalnych rozwiązań. Analiza zmienności strumienia (FVA), wbudowana w niektóre programy analityczne, zwraca granice strumieni przechodzących przez każdą reakcję, co w połączeniu z odpowiednią kombinacją innych strumieni pozwala oszacować optymalne rozwiązanie.

Wizualna i numeryczna reprezentacja FVA w sieci z usuwaniem nieśmiercionośnym.

Reakcje, które mogą wspierać niską zmienność przepływów przez nie, prawdopodobnie będą miały większe znaczenie dla organizmu, a FVA jest obiecującą techniką identyfikacji ważnych reakcji.

Minimalizacja przystosowania metabolicznego (MOMA)

Podczas symulacji nokautów lub wzrostu na pożywce, FBA podaje ostateczny rozkład strumienia w stanie ustalonym. Ten ostateczny stan ustalony jest osiągany w różnych skalach czasowych. Na przykład przewidywane tempo wzrostu E. coli na glicerolu jako głównym źródle węgla nie odpowiadało przewidywaniom FBA; jednak w przypadku podkultury przez 40 dni lub 700 pokoleń tempo wzrostu ewoluowało adaptacyjnie, aby dopasować się do przewidywań FBA.

Czasami warto dowiedzieć się, jaki jest bezpośredni skutek zakłócenia lub nokautu, ponieważ potrzeba czasu, aby zaszły zmiany regulacyjne i organizm przeorganizował strumienie, aby optymalnie wykorzystać inne źródło węgla lub obejść efekt Nokaut. MOMA przewiduje natychmiastowy suboptymalny rozkład strumienia po zaburzeniu, minimalizując odległość (euklidesową) między rozkładem strumienia FBA typu dzikiego a rozkładem strumienia zmutowanego za pomocą programowania kwadratowego. Daje to problem optymalizacji formularza.

${\ Displaystyle \ min \ ||\ mathbf {v_ {w}} - \ mathbf {v_ {d}} || ^ {2} \ qquad st \ quad \ mathbf {S} \ cdot \ mathbf {v_{d}} =0}$

gdzie ${\ Displaystyle \ mathbf {v_ {w}}}$ reprezentuje rozkład strumienia typu dzikiego (lub stanu niezakłóconego), a ${\ Displaystyle \ mathbf {v_ {d}}}$ reprezentuje rozkład strumienia po usunięciu genu, który jest do rozwiązania. Upraszcza to:

${\ Displaystyle \ min \ {\ Frac {1} {2}} \ {\ mathbf {v_ {d}}} ^ {T} \ \ mathbf {I} \ \ mathbf {v_ {d}} +(\mathbf {-v_{w}} )\cdot \mathbf {v_{d}} \qquad st\quad \mathbf {S} \cdot \mathbf {v_{d}} =0}$

Jest to rozwiązanie MOMA, które przedstawia rozkład strumienia bezpośrednio po perturbacji.

Regulacyjna minimalizacja włącz-wyłącz (ROOM)

ROOM próbuje poprawić przewidywanie stanu metabolicznego organizmu po nokaucie genu. Opiera się na tym samym założeniu, co MOMA, że organizm próbowałby przywrócić rozkład przepływu jak najbardziej zbliżony do typu dzikiego po nokaucie. Jednak dalej stawia się hipotezę, że ten stan ustalony zostałby osiągnięty poprzez serię przejściowych zmian metabolicznych w sieci regulacyjnej i że organizm próbowałby zminimalizować liczbę zmian regulacyjnych wymaganych do osiągnięcia stanu typu dzikiego. Jednak zamiast minimalizacji metryki odległości wykorzystuje metodę programowania liniowego mieszanych liczb całkowitych.

Dynamiczny FBA

Dynamiczny FBA próbuje dodać możliwość zmiany modeli w czasie, unikając w ten sposób w pewnym sensie ścisłego stanu ustalonego czystego FBA. Zazwyczaj technika ta polega na przeprowadzeniu symulacji FBA, zmianie modelu w oparciu o wyniki tej symulacji i ponownym uruchomieniu symulacji. Powtarzając ten proces, z czasem uzyskuje się element sprzężenia zwrotnego.

Porównanie z innymi technikami

FBA zapewnia mniej uproszczoną analizę niż analiza punktów przewężenia, wymagając jednocześnie znacznie mniej informacji na temat szybkości reakcji i znacznie mniej kompletnej rekonstrukcji sieci niż wymagałaby tego pełna symulacja dynamiczna. Wypełniając tę niszę, wykazano, że FBA jest bardzo przydatną techniką do analizy możliwości metabolicznych systemów komórkowych.

Analiza punktu przewężenia

W przeciwieństwie do analizy wąskich gardeł, która uwzględnia tylko punkty w sieci, w których metabolity są produkowane, ale nie są konsumowane lub odwrotnie, FBA jest prawdziwą formą modelowania sieci metabolicznej , ponieważ traktuje sieć metaboliczną jako pojedynczą kompletną całość ( macierz stechiometryczna ) na wszystkich etapach analizy. Oznacza to, że w modelu można odtworzyć efekty sieciowe, takie jak reakcje chemiczne w odległych ścieżkach, które wpływają na siebie nawzajem. Zaletą niezdolności analizy wąskich gardeł do symulacji efektów sieciowych jest to, że rozważa każdą reakcję w sieci w izolacji, a zatem może sugerować ważne reakcje w sieci, nawet jeśli sieć jest bardzo pofragmentowana i zawiera wiele luk.

Dynamiczna symulacja metaboliczna

W przeciwieństwie do dynamicznej symulacji metabolicznej, FBA zakłada, że wewnętrzne stężenie metabolitów w systemie pozostaje stałe w czasie, a zatem nie jest w stanie zapewnić niczego innego niż rozwiązania w stanie ustalonym. Jest mało prawdopodobne, aby FBA mogło na przykład symulować funkcjonowanie komórki nerwowej. Ponieważ wewnętrzne stężenie metabolitów nie jest uwzględniane w modelu, możliwe jest, że roztwór FBA może zawierać metabolity w stężeniu zbyt wysokim, aby było biologicznie dopuszczalne. Jest to problem, którego prawdopodobnie uniknęłyby dynamiczne symulacje metaboliczne. Jedną z zalet prostoty FBA w porównaniu z symulacjami dynamicznymi jest to, że są one znacznie mniej kosztowne obliczeniowo, umożliwiając symulację dużej liczby zakłóceń w sieci. Drugą zaletą jest to, że zrekonstruowany model może być znacznie prostszy dzięki uniknięciu konieczności uwzględniania szybkości enzymów i wpływu złożonych interakcji na kinetykę enzymów.

Zobacz też