Automat przesuwający

Klasy automatów

(Kliknięcie na każdą warstwę powoduje wyświetlenie artykułu na ten temat)

W teorii obliczeń , gałęzi informatyki teoretycznej , automat ze stosem ( PDA ) jest rodzajem automatu wykorzystującego stos .

Automaty ze stosem są wykorzystywane w teoriach dotyczących tego, co mogą być obliczone przez maszyny. Mają większe możliwości niż maszyny o skończonych stanach , ale mniej wydajne niż maszyny Turinga (patrz poniżej ). Deterministyczne automaty ze stosem mogą rozpoznać wszystkie deterministyczne języki bezkontekstowe, podczas gdy niedeterministyczne mogą rozpoznać wszystkie języki bezkontekstowe , przy czym ten pierwszy jest często używany w projektowaniu parserów .

Termin „wsuwanie” odnosi się do faktu, że stos można uznać za „wsuwany w dół” jak dozownik tac w stołówce, ponieważ operacje te nigdy nie dotyczą elementów innych niż element górny. Z kolei automat stosowy umożliwia dostęp do głębszych elementów i wykonywanie operacji na nich. Automaty stosowe rozpoznają znacznie większy zestaw języków niż automaty ze stosem. automat stosowy umożliwia pełny dostęp, a także pozwala, aby wartości skumulowane były całymi stosami podrzędnymi, a nie tylko pojedynczymi, skończonymi symbolami.

Nieformalny opis

Schemat automatu ze stosem

Maszyna o skończonych stanach po prostu patrzy na sygnał wejściowy i bieżący stan: nie ma stosu, z którym mogłaby pracować. Wybiera nowy stan, będący wynikiem przejścia. Automat ze stosem (PDA) różni się od maszyny skończonej pod dwoma względami:

Może użyć wierzchołka stosu, aby zdecydować, które przejście wybrać.
Może manipulować stosem w ramach wykonywania przejścia.

Automat ze stosem czyta zadany ciąg wejściowy od lewej do prawej. Na każdym etapie wybiera przejście, indeksując tabelę według symbolu wejściowego, bieżącego stanu i symbolu na górze stosu. Automat ze stosem może również manipulować stosem w ramach wykonywania przejścia. Manipulacja może polegać na wypchnięciu określonego symbolu na szczyt stosu lub wyskoczeniu z wierzchu stosu. Automat może alternatywnie zignorować stos i pozostawić go bez zmian.

Połączone: Mając symbol wejściowy, bieżący stan i symbol stosu, automat może podążać za przejściem do innego stanu i opcjonalnie manipulować (wpychać lub otwierać) stosem.

Jeżeli w każdej sytuacji możliwa jest co najwyżej jedna taka akcja przejścia, wówczas automat nazywa się deterministycznym automatem ze stosem (DPDA) . Ogólnie rzecz biorąc, jeśli możliwych jest kilka działań, wówczas automat nazywa się ogólnym lub niedeterministycznym PDA . Dany ciąg wejściowy może skierować niedeterministyczny automat ze stosem do jednej z kilku sekwencji konfiguracyjnych; jeśli jeden z nich po odczytaniu całego ciągu wejściowego prowadzi do konfiguracji akceptującej, mówimy, że ten ostatni należy do języka akceptowanego przez automat .

Definicja formalna

Używamy standardowej notacji języka formalnego $oznacza$ $zbiór$ ciągów o skończonej nad $.$ i pusty ciąg

PDA jest formalnie zdefiniowane jako 7-krotka:

$M = (Q, \ Sigma, \ Gamma, \ delta, q_ {0}, Z, F)}$ Displaystyle

jest $skończonym$ zbiorem
$wejściowym$ zbiorem nazywanym alfabetem
$skończonym$ nazywanym alfabetem stosu
${\ Displaystyle \ delta}$ jest skończonym podzbiorem ${\ Displaystyle Q \ razy (\ Sigma \ puchar \ {\ varepsilon \}) \ razy \ Gamma \times Q\times \Gamma ^{*}}$ , relacja przejścia
${\ displaystyle q_ {0} \ w Q}$ jest stanem początkowym
$stosu$ _ _
$akceptujących$ _ _

Element $_$ $_$ _ _ Ma zamierzone znaczenie, że $} varepsilon \}}$ wejściu za $\ displaystyle$ $displaystyle p \ in$ i mając $stosu$ , może odczytać $}$ zmienić stan na , pop , zastępując go za $A \ in \$ $displaystyle$ pchanie $}$ } $(\ Sigma \ Puchar \ {\ varepsilon \})}$ Displaystyle Składnik relacji przejścia służy do sformalizowania, że PDA może albo odczytać literę z wejścia, albo pozostawić wejście nietknięte. ^{[ potrzebne źródło ]}

W wielu tekstach relację przejściową zastępuje się (równoważną) formalizacją, gdzie

jest funkcją przejścia $,$ mapującą $\ Gamma}$ na skończone podzbiory z ${\ Displaystyle Q \ razy \ Gamma ^ {*}}$

Tutaj zawiera wszystkie możliwe akcje w stanie, w którym znajduje się na stosie, podczas czytania a $displaystyle \ delta (p, a, A)} δ ( p ,$ $\$ \ $, a, A)$ $} styl wyświetlania a}$ na wejściu. Pisze się na przykład ${\ Displaystyle \ delta (p, a, A) = \ {(q, BA) \}}$ dokładnie wtedy, gdy ${\ Displaystyle (q, BA) \ in \ {(q, BA) \}, (q, BA) \ in \ delta (p, a, A),}$ ponieważ ${\ Displaystyle ((p, a, A), \ {(q, BA) \}) \ in \ delta}$ . Zauważ, że skończoność w tej definicji jest niezbędna.

Obliczenia

stopień automatu ze stosem

W celu sformalizowania semantyki automatu ze stosem w dół wprowadzony został opis aktualnej sytuacji. Dowolna 3-krotka ${\ Displaystyle (p, w, \ beta) \ in Q \ razy \ Sigma ^ {*} \ razy \ Gamma ^ {*}}$ nazywa się natychmiastowym opisem (ID) ${\ displaystyle M}$ , który obejmuje bieżący stan, część taśmy wejściowej, która nie została odczytana, oraz zawartość stosu (najwyższy symbol zapisany jako pierwszy). Relacja $opisach$ $.$ $_$ krokową chwilowych _ Dla instrukcji ${\ Displaystyle (p, a, A, q, \ alfa) \ in \ delta}$ istnieje krok $} ,$ ${\ Displaystyle (p, topór, A \ gamma) \ vdash _ {M} (q, x, \ alfa \ gamma$ $}}$ każdego i każdego $x$ \ Displaystyle x \ in \ Sigma ^ {

$stosem są$ że w danym chwilowym opisie może być kilka W obliczeniach można wybrać dowolny z tych etapów. Przy powyższej definicji w każdym kroku zawsze pojawia się pojedynczy symbol (na górze stosu), zastępując go dowolną liczbą symboli. W konsekwencji żaden krok nie jest zdefiniowany, gdy stos jest pusty.

Obliczenia automatu ze stosem to sekwencje kroków. Obliczenia rozpoczynają się w stanie początkowym $Z}$ $Z$ symbolem stosu ${\ Displaystyle (q_ {0}, w, Z)}$ stosie i ciągiem na taśmie wejściowej, a więc z początkowym opisem ( $displaystyle$ . Istnieją dwa sposoby akceptacji. Automat ze stosem albo akceptuje stan końcowy, co oznacza, że po przeczytaniu danych wejściowych automat osiąga stan akceptacji (w $,$ albo akceptuje pusty stos ( $,$ co oznacza, że po czytając dane wejściowe, automat opróżnia swój stos. Pierwszy tryb akceptacji korzysta z pamięci wewnętrznej (stanu), drugi z pamięci zewnętrznej (stosu).

Formalnie definiuje się

${\ Displaystyle L (M) = \ {w \ in \ Sigma ^ {*} | (q_ {0}, w, Z) \ vdash _ {M} ^ {*} (f, \ varepsilon, \ gamma)}$ z ${\ displaystyle f \ in F}$ i ${\ displaystyle \ gamma \ in \ Gamma ^ {*} \} }$ (stan końcowy)
${\ Displaystyle N (M) = \ {w \ in \ Sigma ^ {*} | (q_ {0}, w, Z) \ vdash _ {M} ^ {*} (q, \ varepsilon, \ varepsilon)}$ z ${\ Displaystyle q \ w Q \}}$ (pusty stos)

Tutaj reprezentuje odruchowe i przechodnie domknięcie relacji krokowej, $*}}$ oznacza dowolną liczbę kolejnych kroków (zero, jeden) ${\ displaystyle \ vdash _ {M} ^$ albo więcej).

Dla każdego pojedynczego automatu ze stosem te dwa języki nie muszą mieć żadnego związku: mogą być równe, ale zwykle tak nie jest. Specyfikacja automatu powinna zawierać także zamierzony sposób odbioru. Przejęte wszystkie automaty ze stosem, oba warunki akceptacji definiują tę samą rodzinę języków.

Twierdzenie. Dla każdego automatu ze stosem można skonstruować automat ze stosem $L (M) = N (M')$ $M$ że ${ \$ $w$ odwrotnie, dla każdego automatu ze stosem $skonstruować$ automat ze stosem sposób, że ${\ Displaystyle N (M) = L (M ')}$

Przykład

Poniżej znajduje się formalny opis PDA, który rozpoznaje język według stanu końcowego: ${\ displaystyle \ {0 ^ {n} 1 ^ {n} \ mid n \ geq 0 \}}$

PDA dla

{\ Displaystyle \ {0 ^ {n} 1 ^ {n} \ mid n \ geq 0 \}}

(według stanu końcowego)

${\ Displaystyle M = (Q, \ \ Sigma, \ \ Gamma, \ \ delta, \ q_ {0}, \ Z, \ F)}$ , Gdzie

stwierdza: ${\ displaystyle Q = \ {p, q, r \}}$
alfabet wejściowy: ${\ Displaystyle \ Sigma = \ {0,1 \}}$
alfabet stosu: ${\ Displaystyle \ Gamma = \ {A, Z \}}$
stan początkowy: ${\ displaystyle q_ {0} = p}$
symbol stosu początkowego: $Z$
akceptując stany: ${\ displaystyle F = \ {r \}}$

Relacja przejścia składa się z następujących sześciu instrukcji: ${\ displaystyle \ delta}$

{\ Displaystyle (p, 0, Z, p, AZ)}

,

{\ Displaystyle (p, 0, A, p, AA)}

,

{\ Displaystyle (p, \ epsilon, Z, q, Z)}

,

{\ Displaystyle (p, \ epsilon, A, q, A)}

,

{\ Displaystyle (q, 1, A, q, \ epsilon)}

i

{\ Displaystyle (q, \ epsilon, Z, r, Z)}

.

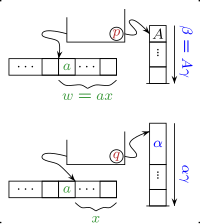
0 Inaczej mówiąc, pierwsze dwie instrukcje mówią, że w stanie $p$ za każdym razem, gdy odczytywany jest symbol , jedno $A$ jest odkładane na stos. Naciśnięcie symbolu $A$ na inny $A$ jest sformalizowane jako zastąpienie góry $A$ przez $AA$ (i podobnie w przypadku nałożenia symbolu $A$ na $Z$ ).

Instrukcja trzecia i czwarta mówią, że w dowolnym momencie automat może przejść ze stanu $p$ do stanu $q$ .

Piąta instrukcja mówi, że w stanie $q$ , na każdy odczytany symbol 1 , wyskakuje jedno $A.$

Wreszcie szósta instrukcja mówi, że maszyna może przejść ze stanu q $do$ zaakceptowania stanu $r$ tylko wtedy, gdy stos składa się z pojedynczego $Z.$

Wydaje się, że nie ma powszechnie używanej reprezentacji PDA. $przez$ przedstawiliśmy od $q$ _ $_$ _ ${\ displaystyle a; A / \ alfa}$ (przeczytaj $a$ ; zamień $A$ na ${\ displaystyle \ alfa}$ ).

Zrozumienie procesu obliczeniowego

akceptuję obliczenia dla 0011

Poniżej ilustruje sposób, w jaki powyższy PDA wykonuje obliczenia na różnych ciągach wejściowych. Indeks dolny $M$ $jest$ symbolu kroku tutaj pominięty.

Ciąg wejściowy = 0011. Istnieją różne obliczenia w zależności od momentu przejścia ze stanu p do stanu q . Tylko jeden z nich akceptuje.
1. ${\ Displaystyle (p, 0011, Z) \ vdash (q, 0011, Z) \ vdash (r, 0011, Z )}$ Stan końcowy to akceptacja, ale wejście nie jest akceptowane w ten sposób, ponieważ nie zostało odczytane.
2. ${\ Displaystyle (p, 0011, Z) \ vdash (p, 011, AZ) \ vdash (q, 011 ,AZ)}$ Dalsze kroki nie są możliwe.
3. ${\ Displaystyle (p, 0011, Z) \ vdash (p, 011, AZ) \ vdash (p, 11, AAZ) \ vdash (q, 11, AAZ) \ vdash (q, 1,AZ)\vdash (q,\epsilon ,Z)\vdash (r,\epsilon ,Z)}$ Akceptowanie obliczeń: kończy się stanem akceptacji, po odczytaniu wszystkich danych wejściowych.
Ciąg wejściowy = 00111. Ponownie istnieją różne obliczenia. Żadne z nich nie akceptuje.
1. ${\ Displaystyle (p, 00111, Z) \ vdash (q, 00111, Z) \ vdash (r, 00111, Z )}$ Stan końcowy to akceptacja, ale wejście nie jest akceptowane w ten sposób, ponieważ nie zostało odczytane.
2. ${\ Displaystyle (p, 00111, Z) \ vdash (p, 0111, AZ) \ vdash (q, 0111 ,AZ)}$ Dalsze kroki nie są możliwe.
3. ${\ Displaystyle (p, 00111, Z) \ vdash (p, 0111, AZ) \ vdash (p, 111, AAZ) \ vdash (q, 111, AAZ) \ vdash (q ,11,AZ)\vdash (q,1,Z)\vdash (r,1,Z)}$ Stan końcowy akceptuje, ale dane wejściowe nie są w ten sposób akceptowane, gdyż nie zostały (całkowicie) odczytane.

PDA i języki bezkontekstowe

Każdą gramatykę bezkontekstową można przekształcić w równoważny niedeterministyczny automat ze stosem. Proces wyprowadzania gramatyki jest symulowany w sposób skrajnie lewy. Tam, gdzie gramatyka przepisuje nieterminal, PDA bierze najwyższy nieterminal ze swojego stosu i zastępuje go prawą częścią reguły gramatycznej ( rozwiń ). Tam, gdzie gramatyka generuje symbol końcowy, PDA odczytuje symbol z wejścia, gdy jest to najwyższy symbol na stosie ( dopasowanie ). W pewnym sensie stos PDA zawiera nieprzetworzone dane gramatyczne, odpowiadające przechodzeniu drzewa derywacyjnego w kolejności wstępnej.

Technicznie rzecz biorąc, biorąc pod uwagę gramatykę bezkontekstową, PDA ma pojedynczy stan, 1, a jego relacja przejścia jest skonstruowana w następujący sposób.

${\ Displaystyle (1, \ varepsilon, A, 1, \ alfa)}$ dla każdej reguły ${\ Displaystyle A \ do \ alfa}$ ( rozwiń )
${\ Displaystyle (1, a, a, 1, \ varepsilon)}$ dla każdego symbolu końcowego ${\ displaystyle a}$ ( dopasowanie )

PDA akceptuje pusty stos. Jego początkowy symbol stosu jest symbolem początkowym gramatyki. ^{[ potrzebne źródło ]}

Dla gramatyki bezkontekstowej w postaci normalnej Greibacha zdefiniowanie (1,γ) ∈ δ(1, a , A ) dla każdej reguły gramatycznej A → a γ również daje równoważny niedeterministyczny automat ze stosem.

Odwrotnie, znalezienie gramatyki dla danego PDA nie jest takie proste. Sztuka polega na zakodowaniu dwóch stanów PDA w nieterminalach gramatyki.

Twierdzenie. Dla każdego automatu ze stosem $G)}$ . $L$ sol ) $($

Język ciągów akceptowany przez deterministyczny automat ze stosem (DPDA) nazywany jest deterministycznym językiem bezkontekstowym . Nie wszystkie języki bezkontekstowe są deterministyczne. W konsekwencji DPDA jest ściśle słabszą odmianą PDA. Nawet w przypadku języków regularnych istnieje problem eksplozji rozmiaru: dla dowolnej $funkcji$ $dla$ i dowolnie dużych liczb całkowitych $PDA$ o rozmiarze język regularny. którego najmniejszy DPDA ma co najmniej ${\ displaystyle f (n)}$ stany. W przypadku wielu nieregularnych PDA każdy równoważny DPDA wymagałby nieograniczonej liczby stanów.

Automat skończony z dostępem do dwóch stosów jest urządzeniem o większej mocy, porównywalnym pod względem mocy z maszyną Turinga . Automat z ograniczeniami liniowymi to urządzenie, które ma większą moc niż automat ze stosem, ale mniej niż maszyna Turinga.

Maszyny PDA i Turinga

Automat ze stosem jest obliczeniowo równoważny „ograniczonej” maszynie Turinga (TM) z dwiema taśmami, która jest ograniczona w następujący sposób: na pierwszej taśmie TM może tylko czytać dane wejściowe i poruszać się od lewej do prawej (nie może wprowadzać zmian ). Na drugiej taśmie może jedynie przesyłać i przesyłać dane. Lub równoważnie, może czytać, pisać i poruszać się w lewo i w prawo, z zastrzeżeniem, że jedyną akcją, jaką może wykonać na każdym kroku, jest albo usunięcie skrajnego lewego znaku w ciągu (pop), albo dodanie dodatkowego znaku po lewej stronie -najwięcej znaków w ciągu (push).

To, że PDA jest słabszy od TM, można sprowadzić do tego, że procedura „pop” usuwa część danych. Aby uczynić PDA tak mocnym jak TM, musimy gdzieś zapisać dane utracone w wyniku „pop”. Możemy to osiągnąć wprowadzając drugi stos. W modelu TM PDA z ostatniego akapitu jest to odpowiednik pamięci TM z 3 taśmami, gdzie pierwsza taśma jest taśmą wejściową tylko do odczytu, a druga i trzecia taśma to taśmy typu „push and pop” (stos) . Aby taki PDA symulował dowolną daną TM, podajemy wejście PDA na pierwszą taśmę, pozostawiając oba stosy puste. Następnie następuje wypychanie całego sygnału wejściowego z taśmy wejściowej na pierwszy stos. Kiedy cały sygnał wejściowy zostanie przeniesiony na pierwszy stos, teraz postępujemy jak w przypadku normalnej TM, gdzie poruszanie się w prawo po taśmie jest równoznaczne z wyrzuceniem symbolu z pierwszego stosu i wepchnięciem (prawdopodobnie zaktualizowanego) symbolu na drugi stos, i przesunięcie w lewo odpowiada wyjęciu symbolu z drugiego stosu i wepchnięciu (prawdopodobnie zaktualizowanego) symbolu do pierwszego stosu. Mamy zatem PDA z 2 stosami, które mogą symulować dowolną TM.

Uogólniony automat ze stosem (GPDA)

GPDA to urządzenie PDA, które zapisuje na stosie cały ciąg o znanej długości lub usuwa cały ciąg ze stosu w jednym kroku.

GPDA jest formalnie zdefiniowane jako 6-krotka:

{\ Displaystyle M = (Q, \ \ Sigma, \ \ Gamma, \ \ delta, \ q_ {0}, \ F)}

gdzie $_$ w $taki$ .

{\ Displaystyle \, \ delta}

:

{\ Displaystyle Q \ razy \ Sigma _ {\ epsilon} \ razy \ Gamma ^ {*} \ longrightarrow P ( Q\times \Gamma ^{*})}

jest funkcją przejścia.

$1}$ GPDA są takie same jak dla PDA, z tą różnicą, że $+$ { \ zamiast symboli.

GPDA i PDA są równoważne pod tym względem, że jeśli język jest rozpoznawany przez PDA, jest on również rozpoznawany przez GPDA i odwrotnie.

Można sformułować analityczny dowód równoważności GPDA i PDA, korzystając z następującej symulacji:

Niech ${\ Displaystyle \ delta (q_ {1}, w, x_ {1} x_$ będzie przejściem GPDA

gdzie ${\ Displaystyle q_ {1}, q_ {2} \ in Q, w \ in \ Sigma _ {\ epsilon}, x_ {1}, x_ {2}, \ ldots, x_ {m} \ in \ Gamma ^ { *},m\geq 0,y_{1},y_{2},\ldots ,y_{n}\in \Gamma ^{*},n\geq 0}$ .

Skonstruuj następujące przejścia dla PDA:

{\ Displaystyle {\ początek {tablica} {lcl} \ delta '(q_ {1}, w, x_ {1}) i \ longrightarrow & (p_ {1}, \ epsilon) \\\ delta '(p_ {1} },\epsilon ,x_{2})&\longrightarrow &(p_{2},\epsilon )\\&\vdots &\\\delta '(p_{m-1},\epsilon ,x_{m}) &\longrightarrow &(p_{m},\epsilon )\\\delta '(p_{m},\epsilon ,\epsilon )&\longrightarrow &(p_{m+1},y_{n})\\\ delta '(p_{m+1},\epsilon ,\epsilon )&\longrightarrow &(p_{m+2},y_{n-1})\\&\vdots &\\\delta '(p_{m +n-1},\epsilon ,\epsilon )&\longrightarrow &(q_{2},y_{1}).\end{array}}}

Automat stosowy

Jako uogólnienie automatów ze stosem, Ginsburg, Greibach i Harrison (1967) zbadali automaty stosowe , które mogą dodatkowo przesuwać się w lewo lub w prawo w ciągu wejściowym (otoczonym specjalnymi symbolami znaczników końcowych, aby zapobiec wyślizgiwaniu się) oraz zwiększać lub zmniejszać stos w trybie tylko do odczytu. Automat stosowy nazywany jest niekasującym , jeśli nigdy nie wyskakuje ze stosu. Klasą języków akceptowaną przez niedeterministyczne, niekasujące automaty stosowe jest NSPACE ( n ² ), która jest nadzbiorem języków kontekstowych . Klasą języków akceptowaną przez deterministyczne, niekasujące automaty stosowe jest DSPACE ( n ⋅log( n )).

Automaty ze stosem naprzemiennym

Naprzemienny automat ze stosem ( APDA) to automat ze stosem ze zbiorem stanów

${\ Displaystyle Q = Q _ {\ istnieje} \ Puchar Q _ {\ forall}}$ gdzie ${\ Displaystyle Q _ {\ istnieje} \ czapka Q _ {\ forall} = \ pusty zestaw }$ .

Stany $są$ i $odpowiednio$ _ _ _ uniwersalny . W stanie egzystencjalnym APDA w sposób niedeterministyczny wybiera następny stan i akceptuje, jeśli co najmniej jedno z wynikowych obliczeń się zgodzi. W stanie uniwersalnym APDA przechodzi do wszystkich kolejnych stanów i akceptuje, jeśli wszystkie wynikowe obliczenia akceptują.

Model został wprowadzony przez Chandrę , Kozena i Stockmeyera . Ladner , Lipton i Stockmeyer udowodnili, że model ten jest równoważny EXPTIME , tj. język jest akceptowany przez jakąś APDA wtedy i tylko wtedy , gdy może zostać określony przez algorytm czasu wykładniczego.

Aizikowitz i Kaminski wprowadzili zsynchronizowane naprzemienne automaty ze stosem (SAPDA), które są równoważne gramatykom koniunktywnym w taki sam sposób, jak niedeterministyczne PDA są równoważne gramatykom bezkontekstowym.

Zobacz też

Notatki

^ ^abc ^John ^; E. Hopcroft Jeffrey D. Ullman (1967). „Niekasujące automaty stosowe” . Journal of Computer and System Sciences . 1 (2): 166–186. doi : 10.1016/s0022-0000(67)80013-8 .
^ ^a ^b ^c ^d ^e ^f John E. Hopcroft i Jeffrey D. Ullman (1979). Wprowadzenie do teorii automatów, języków i obliczeń . Czytanie/MA: Addison-Wesley. ISBN 0-201-02988-X .
^ Johna E. Hopcrofta; Rajeev Motwani; Jeffreya D. Ullmana (2003). Wprowadzenie do teorii automatów, języków i obliczeń . Addisona Wesleya. Tutaj: Sekcja 6.4.3, s. 249
^ Holzer, Markus; Kutrib, Martin (2019). „Nierekurencyjne kompromisy są „prawie wszędzie” ”. Obliczenia z prognozowaniem i przemysłem . 11558 : 25–36. doi : 10.1007/978-3-030-22996-2_3 . Wynika to z cytowanego [22, Twierdzenie 7] i stwierdzonej obserwacji, że dowolny deterministyczny automat ze stosem można przekształcić w równoważny automat skończony ^{[ wyjaśnij ]} o wielkości co najwyżej podwójnie wykładniczej.
^ Seymour Ginsburg, Sheila A. Greibach i Michael A. Harrison (1967). „Automaty stosowe i kompilacja” . J.ACM . 14 (1): 172–201. doi : 10.1145/321371.321385 .
^ Seymour Ginsburg, Sheila A. Greibach i Michael A. Harrison (1967). „Automaty ze stosem jednokierunkowym”. J.ACM . 14 (2): 389–418. doi : 10.1145/321386.321403 .
^ Chandra, Ashok K.; Kozen, Dexter C.; Stockmeyer, Larry J. (1981). "Alternacja". Dziennik ACM . 28 (1): 114–133. doi : 10.1145/322234.322243 . ISSN 0004-5411 .
^ Ladner, Richard E.; Lipton, Richard J.; Stockmeyer, Larry J. (1984). „Naprzemienne automaty ze przesuwaniem i układaniem stosów”. SIAM Journal on Computing . 13 (1): 135–155. doi : 10.1137/0213010 . ISSN 0097-5397 .
^ Aizikowitz, Tamar; Kamiński, Michał (2011). „Gramatyki koniunkcyjne LR (0) i deterministyczne zsynchronizowane naprzemienne automaty ze przesuwaniem w dół”. Informatyka – teoria i zastosowania . Notatki z wykładów z informatyki. Tom. 6651. s. 345–358. doi : 10.1007/978-3-642-20712-9_27 . ISBN 978-3-642-20711-2 . ISSN 0302-9743 .

Michaela Sipsera (1997). Wprowadzenie do teorii obliczeń . Wydawnictwo PWS. ISBN 0-534-94728-X . Sekcja 2.2: Automaty ze przesuwaniem, s. 101–114.
Jean-Michel Autebert, Jean Berstel, Luc Boasson, Języki bezkontekstowe i automaty przesuwające w dół , w: G. Rozenberg, A. Salomaa (red.), Handbook of Form Languages, tom. 1, Springer-Verlag, 1997, 111–174.

Linki zewnętrzne

JFLAP , symulator kilku typów automatów, w tym niedeterministycznych automatów ze stosem
CoAn , kolejny symulator dla kilku typów maszyn, w tym niedeterministycznych automatów ze stosem (C++, Windows, Linux, MacOS)

[Hopcroft.Ullman.1967-1] John ^; E. Hopcroft Jeffrey D. Ullman (1967). „Niekasujące automaty stosowe” . Journal of Computer and System Sciences . 1 (2): 166–186. doi : 10.1016/s0022-0000(67)80013-8 .

[Hopcroft.Ullman.1979-2] ^ ^a ^b ^c ^d ^e ^f John E. Hopcroft i Jeffrey D. Ullman (1979). Wprowadzenie do teorii automatów, języków i obliczeń . Czytanie/MA: Addison-Wesley. ISBN 0-201-02988-X .

[3] Johna E. Hopcrofta; Rajeev Motwani; Jeffreya D. Ullmana (2003). Wprowadzenie do teorii automatów, języków i obliczeń . Addisona Wesleya. Tutaj: Sekcja 6.4.3, s. 249

[5] Holzer, Markus; Kutrib, Martin (2019). „Nierekurencyjne kompromisy są „prawie wszędzie” ”. Obliczenia z prognozowaniem i przemysłem . 11558 : 25–36. doi : 10.1007/978-3-030-22996-2_3 . Wynika to z cytowanego [22, Twierdzenie 7] i stwierdzonej obserwacji, że dowolny deterministyczny automat ze stosem można przekształcić w równoważny automat skończony ^{[ wyjaśnij ]} o wielkości co najwyżej podwójnie wykładniczej.

[7] Seymour Ginsburg, Sheila A. Greibach i Michael A. Harrison (1967). „Automaty stosowe i kompilacja” . J.ACM . 14 (1): 172–201. doi : 10.1145/321371.321385 .

[8] Seymour Ginsburg, Sheila A. Greibach i Michael A. Harrison (1967). „Automaty ze stosem jednokierunkowym”. J.ACM . 14 (2): 389–418. doi : 10.1145/321386.321403 .

[ChandraKozen1981-9] Chandra, Ashok K.; Kozen, Dexter C.; Stockmeyer, Larry J. (1981). "Alternacja". Dziennik ACM . 28 (1): 114–133. doi : 10.1145/322234.322243 . ISSN 0004-5411 .

[LadnerLipton1984-10] Ladner, Richard E.; Lipton, Richard J.; Stockmeyer, Larry J. (1984). „Naprzemienne automaty ze przesuwaniem i układaniem stosów”. SIAM Journal on Computing . 13 (1): 135–155. doi : 10.1137/0213010 . ISSN 0097-5397 .

[AizikowitzKaminski2011-11] Aizikowitz, Tamar; Kamiński, Michał (2011). „Gramatyki koniunkcyjne LR (0) i deterministyczne zsynchronizowane naprzemienne automaty ze przesuwaniem w dół”. Informatyka – teoria i zastosowania . Notatki z wykładów z informatyki. Tom. 6651. s. 345–358. doi : 10.1007/978-3-642-20712-9_27 . ISBN 978-3-642-20711-2 . ISSN 0302-9743 .