Brama Toffoli

W obwodach logicznych bramka Toffoliego (również bramka CCNOT ), wynaleziona przez Tommaso Toffoliego , jest uniwersalną odwracalną bramką logiczną , co oznacza, że z bramek Toffoliego można zbudować dowolny klasyczny obwód odwracalny. Znana jest również jako bramka „kontrolowana-kontrolowana-nie”, co opisuje jej działanie. Posiada 3-bitowe wejścia i wyjścia; jeśli pierwsze dwa bity są ustawione na 1, odwraca trzeci bit, w przeciwnym razie wszystkie bity pozostają takie same.

Tło

Wejściowa bramka logiczna L jest odwracalna, jeśli spełnia następujące warunki: L ( x ) = y jest bramką, w której dla dowolnego wyjścia y istnieje unikalne wejście x . Bramka L jest odwracalna, jeśli istnieje bramka L ′( y ) = x , która odwzorowuje y na x . Ze zwykłych bramek logicznych NOT jest odwracalny, jak widać z poniższej tabeli prawdy.

WEJŚCIE	WYJŚCIE
0	1
1	0

Wspólna bramka AND nie jest odwracalna, ponieważ wszystkie wejścia 00, 01 i 10 są mapowane na wyjście 0.

Bramy odwracalne badano od lat 60. XX wieku. Pierwotną motywacją było to, że odwracalne bramki rozpraszają mniej ciepła (lub w zasadzie nie wydzielają ciepła).

Nowsza motywacja pochodzi z komputerów kwantowych . W mechanice kwantowej stan kwantowy może ewoluować na dwa sposoby, przez równanie Schrödingera ( przekształcenia jednostkowe ) lub przez ich załamanie . Operacje logiczne dla komputerów kwantowych, których przykładem jest bramka Toffoliego, są przekształceniami jednostkowymi i dlatego ewoluują w sposób odwracalny.

Uniwersalność i bramka Toffoliego

Każda odwracalna bramka, która zużywa swoje dane wejściowe i umożliwia wszystkie obliczenia wejściowe, nie może mieć więcej bitów wejściowych niż bitów wyjściowych, zgodnie z zasadą przegródki . Dla jednego bitu wejściowego istnieją dwie możliwe odwracalne bramki. Jeden z nich NIE. Druga to bramka tożsamości, która odwzorowuje swoje wejście na wyjście bez zmian. W przypadku dwóch bitów wejściowych jedyną nietrywialną bramką jest kontrolowana bramka NOT , która wykonuje operację XOR pierwszego bitu z drugim bitem i pozostawia pierwszy bit niezmieniony.

Tabela prawdy

Forma macierzy permutacji

WEJŚCIE		WYJŚCIE
0	0	0	0
0	1	0	1
1	0	1	1
1	1	1	0

${\ Displaystyle {\ początek {bmatrix} 1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\\\koniec {bmatrix}}}$

Niestety istnieją funkcje odwracalne, których nie można obliczyć za pomocą tylko tych bramek. Innymi słowy, zbiór składający się z bramek NOT i XOR nie jest uniwersalny . Aby obliczyć dowolną funkcję przy użyciu odwracalnych bramek, potrzebna jest kolejna bramka. Jedną z możliwości jest brama Toffoliego , zaproponowana w 1980 roku przez Toffoliego.

Ta bramka ma 3-bitowe wejścia i wyjścia. Jeśli ustawione są pierwsze dwa bity, trzeci bit jest odwracany. Poniżej znajduje się tabela bitów wejściowych i wyjściowych:

Tabela prawdy

Forma macierzy permutacji

WEJŚCIE			WYJŚCIE
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	0	1
1	1	0	1	1	1
1	1	1	1	1	0

$1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&1&0&0&0&0&0\\0&0&0&1&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0& 0&0&0&1&0&0\\0&0&0&0&0&0&0&1\\0&0&0&0&0&0&1&0\\\koniec{bmacierzy}}}$

Można to również opisać jako odwzorowanie bitów {a, b, c} na {a, b, c XOR (a AND b)}. Można to również rozumieć jako operację Modulo na bicie c: {a, b, c} → {a, b, $(c+ab) mod 2$ } często zapisywane jako {a, b, c} → {a, b, do ${\ Displaystyle \ oplus}$ ab}

Brama Toffoli jest uniwersalna; oznacza to, że dla dowolnej funkcji boolowskiej f ( x ₁ , x ₂ , ..., x _m ) istnieje obwód składający się z bramek Toffoliego, który przyjmuje x ₁ , x ₂ , ..., x _m i zestaw dodatkowych bitów do 0 lub 1 do wyjść x ₁ , x ₂ , ..., x _m , f ( x ₁ , x ₂ , ..., x _m ) i kilka dodatkowych bitów (zwanych śmieciami). Na przykład bramkę NOT można zbudować z bramki Toffoliego, ustawiając trzy bity wejściowe na {a, 1, 1}, tworząc trzeci bit wyjściowy (1 XOR (a AND 1)) = NOT a; (a AND b) jest trzecim bitem wyjściowym z {a, b, 0}. Zasadniczo oznacza to, że można użyć bramek Toffoliego do zbudowania systemów, które wykonają dowolne obliczenia funkcji boolowskiej w sposób odwracalny.

Powiązane bramki logiczne

Bramka Toffoliego może być zbudowana z pojedynczych kubitowych bramek T i Hadamarda oraz co najmniej sześciu CNOT .

Bramka Fredkina to uniwersalna odwracalna 3-bitowa bramka, która zamienia dwa ostatnie bity, jeśli pierwszy bit ma wartość 1; operacja kontrolowanej wymiany.
N - bitowa bramka Toffoliego jest uogólnieniem bramki Toffoliego. Zajmuje n bitów x ₁ , x ₂ , ..., x _n jako wejścia i wyjścia n bitów. Pierwsze n −1 bitów wyjściowych to po prostu x ₁ , ..., x _{n −1} . Ostatnim bitem wyjściowym jest ( x ₁ AND ... AND x _{n −1} ) XOR x _n .
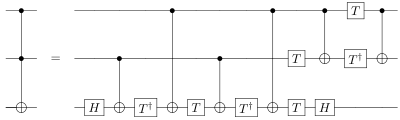
Bramkę Toffoli można zrealizować za pomocą pięciu dwukubitowych bramek kwantowych , ale można wykazać, że nie jest to możliwe przy użyciu mniej niż pięciu.

Powiązana bramka kwantowa, bramka Deutscha , może być zrealizowana przez pięć impulsów optycznych z neutralnymi atomami. Bramka Deutsch jest uniwersalną bramką do obliczeń kwantowych.
Bramka Margolusa (nazwana na cześć Normana Margolusa ), zwana także uproszczoną bramką Toffoli, jest bramką logiki kwantowej bardzo podobną do bramki Toffoliego, ale z -1 na przekątnej: ${\ Displaystyle \ operatorname {RCCX} = \ nazwa operatora {diag} (1,1,1,1,1, -1, X)}$ . Bramka Margolusa jest również uniwersalna dla obwodów odwracalnych i działa bardzo podobnie do bramki Toffoliego, z tą zaletą, że można ją zbudować z około połową CNOTS w porównaniu z bramką Toffoliego.

Związek z komputerami kwantowymi

komputerze kwantowym można zaimplementować dowolną odwracalną bramkę , dlatego też bramka Toffoliego jest również operatorem kwantowym . Jednak bramka Toffoliego nie może być używana do uniwersalnych obliczeń kwantowych, chociaż oznacza to, że komputer kwantowy może realizować wszystkie możliwe klasyczne obliczenia. Bramka Toffoli musi zostać zaimplementowana wraz z niektórymi z natury bramkami kwantowymi, aby była uniwersalna dla obliczeń kwantowych. W rzeczywistości wystarczy dowolna bramka jednokubitowa z rzeczywistymi współczynnikami, która może stworzyć nietrywialny stan kwantowy. Bramka Toffoliego oparta na mechanice kwantowej został pomyślnie zrealizowany w styczniu 2009 roku na Uniwersytecie w Innsbrucku w Austrii. Podczas gdy implementacja n -kubitowego Toffoli z modelem obwodu wymaga 2 n bramek CNOT, najbardziej znana górna granica wynosi 6 n – 12 bramek CNOT. Sugerowano, że uwięzione komputery Ion Quantum mogą być w stanie bezpośrednio zaimplementować n -kubitową bramkę Toffoli. Zastosowanie oddziaływania wielociałowego może być wykorzystane do bezpośredniego działania bramki w uwięzionych jonach, atomach Rydberga i implementacjach obwodów nadprzewodzących. Podążając za rozmaitością stanu ciemnego, Khazali-Mølmer C _n Bramka -NOT działa tylko trzema impulsami, odchodząc od paradygmatu modelu obwodu.

Zobacz też

Linki zewnętrzne

CNOT i Toffoli Gates w ustawieniu Multi-Qubit w projekcie Wolfram Demonstrations.